Уровень
сложности
|
Задания
|
Ответы
|
А
|
1
|
а(а-2)х =а +7
|
При a=2 нет корней;
При a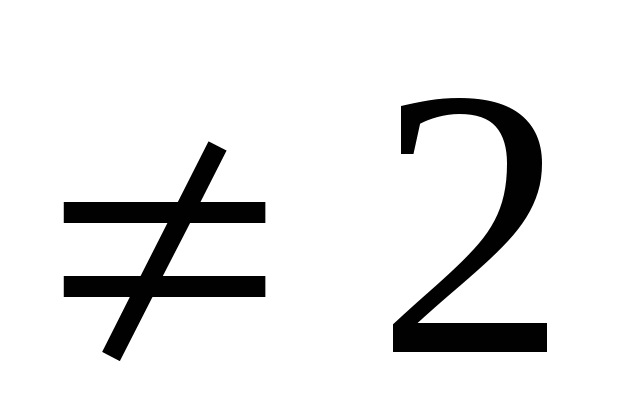 x= x=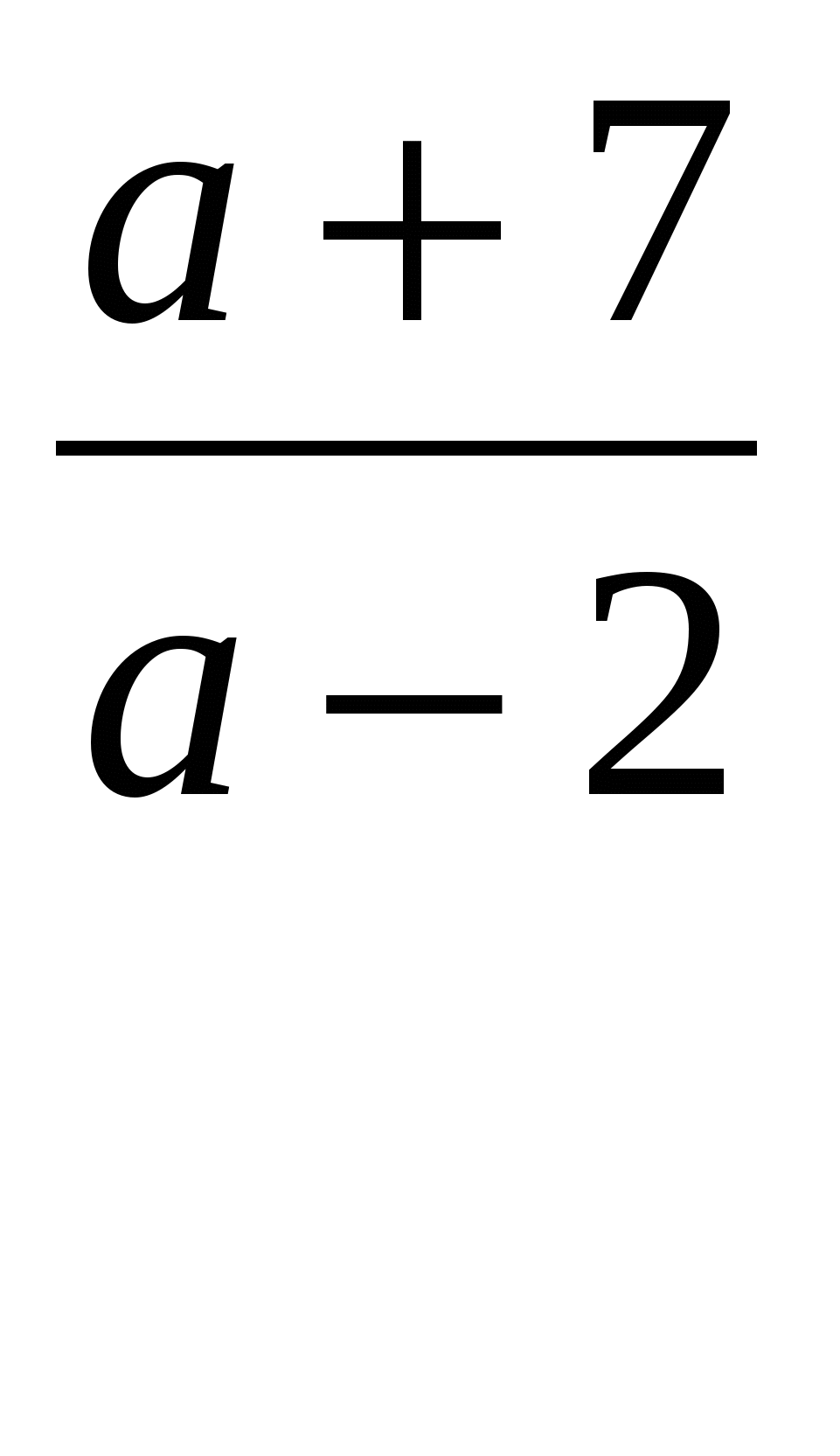
|
|
2
|
2a(a-2)x = a-2
|
При a= 0 нет корней,
При a= 2, x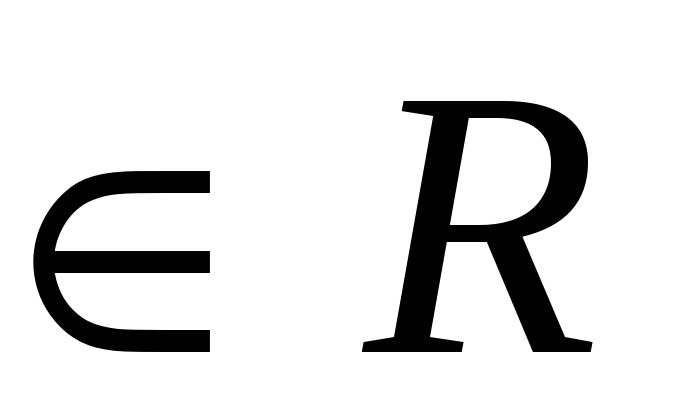 ; ;
При a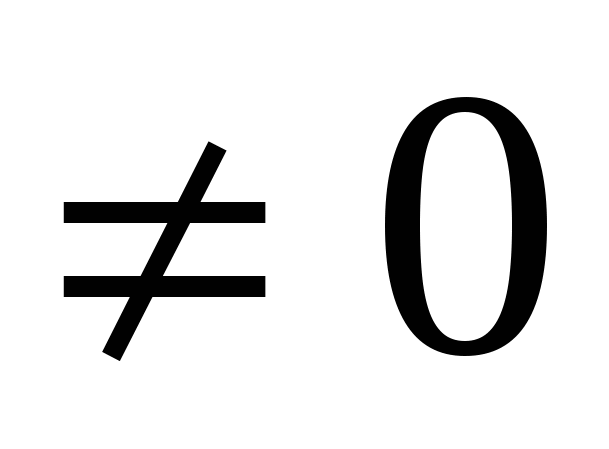 , a , a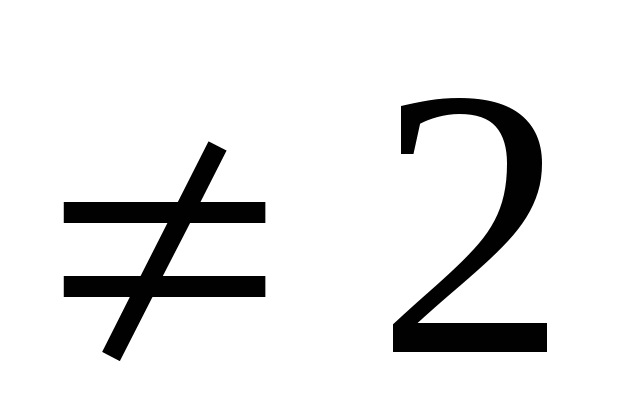 ; x= ; x=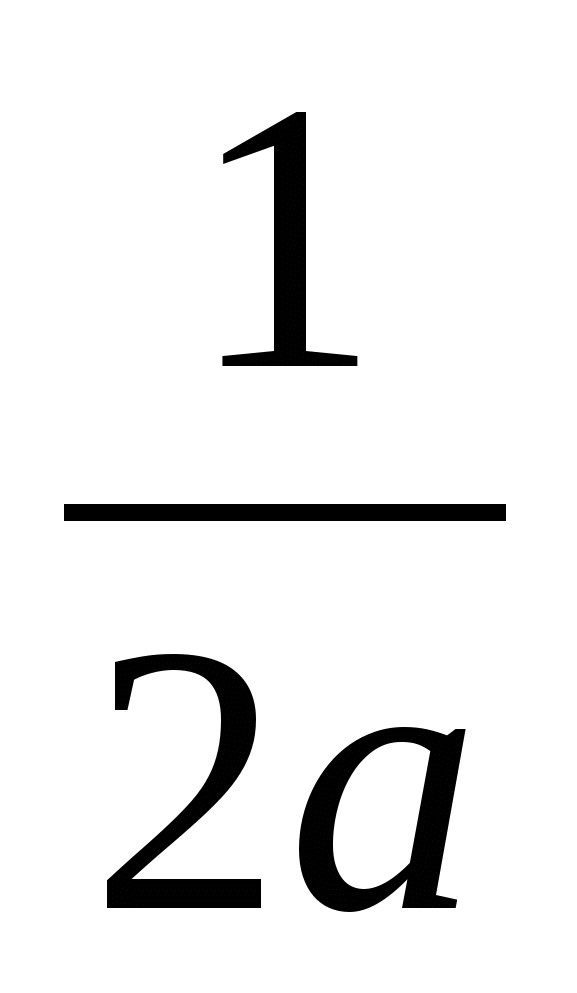
|
|
3
|
Решить уравнение при всех a.
(a-1)x2+2(2a+1)x+(4a+3)=0
|
При a= -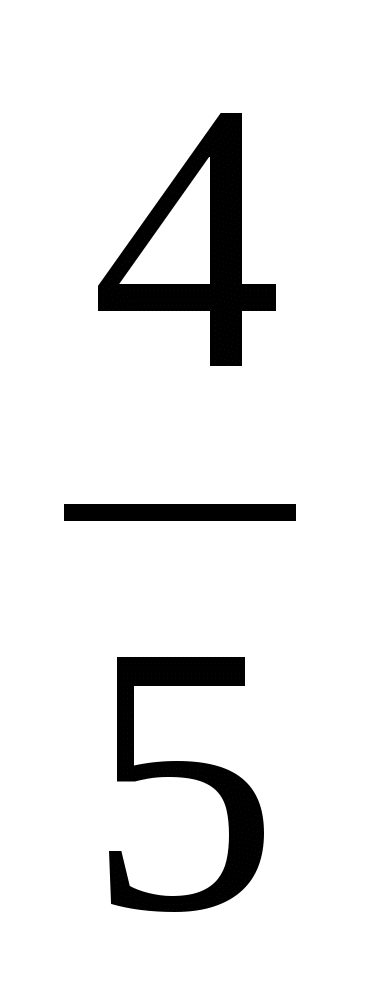 , x= , x= 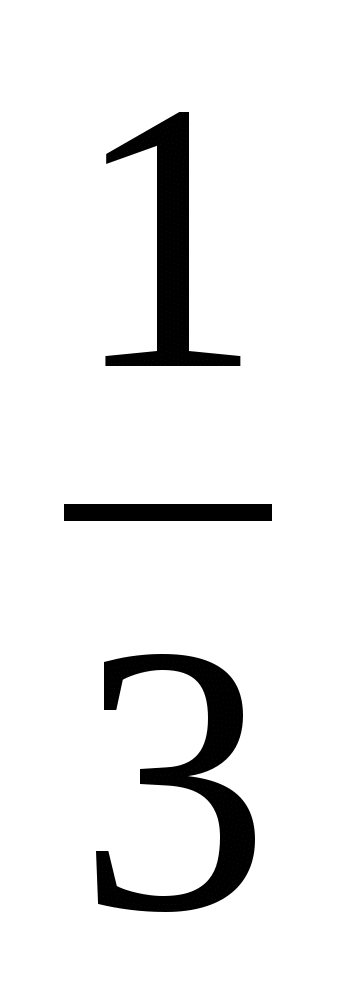 ; ;
При a< -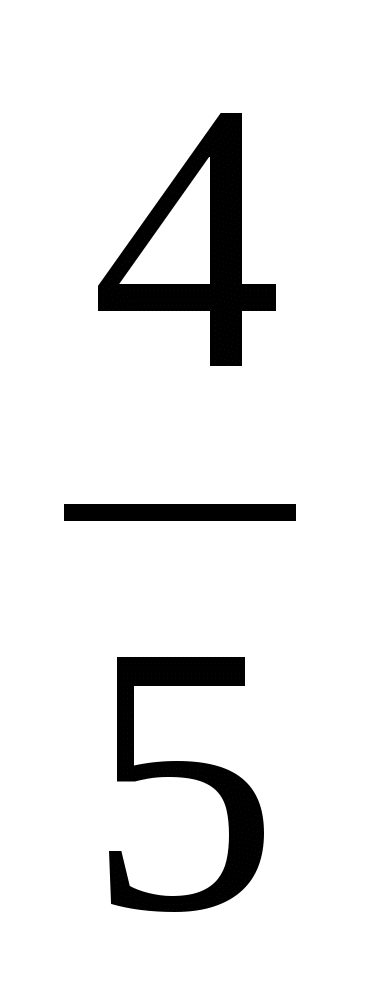 — нет корней; — нет корней;
При a= 1, x= 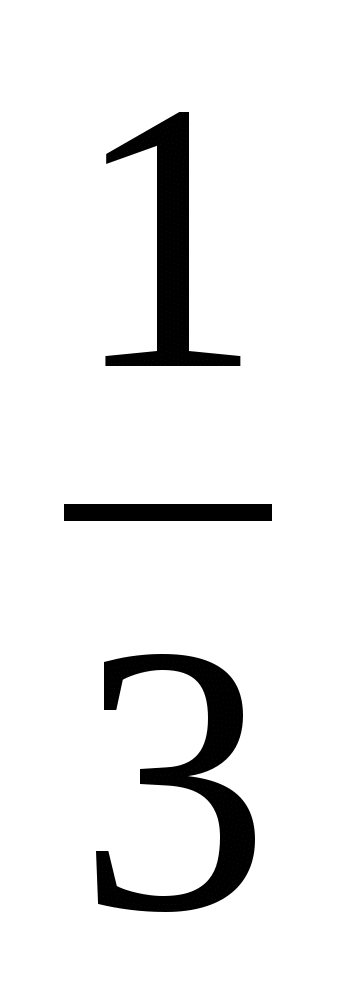 ; ;
При a> -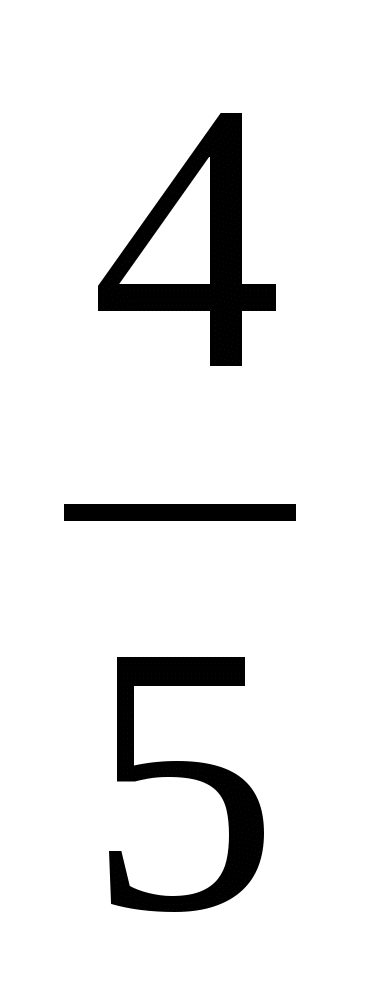 , a , a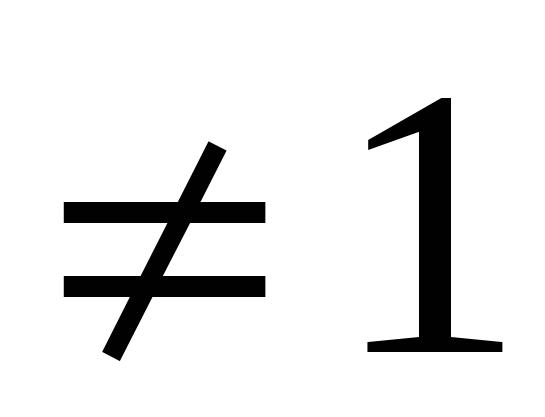
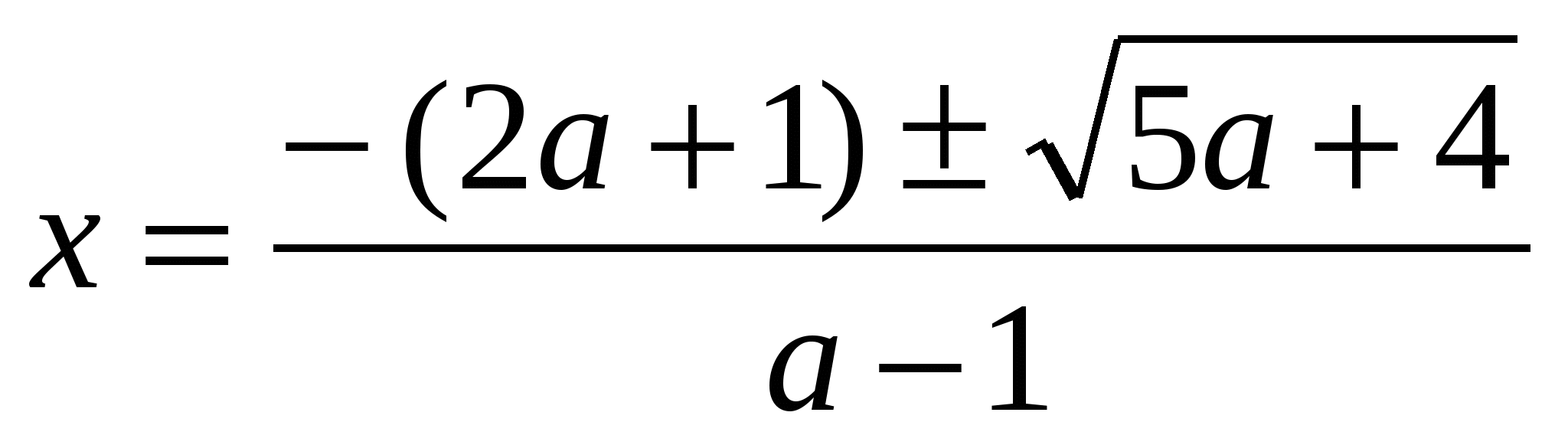
|
B
|
4
|
При каких a уравнение не имеет решений:
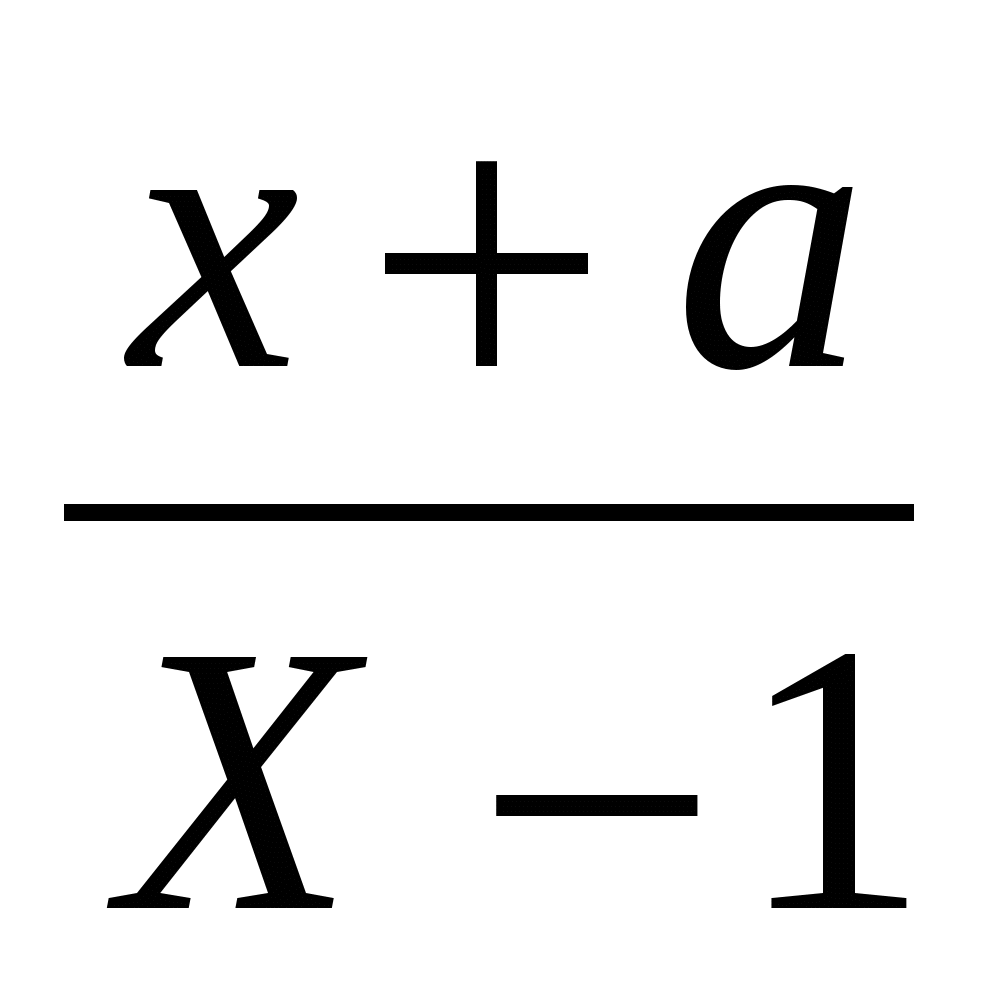 + + 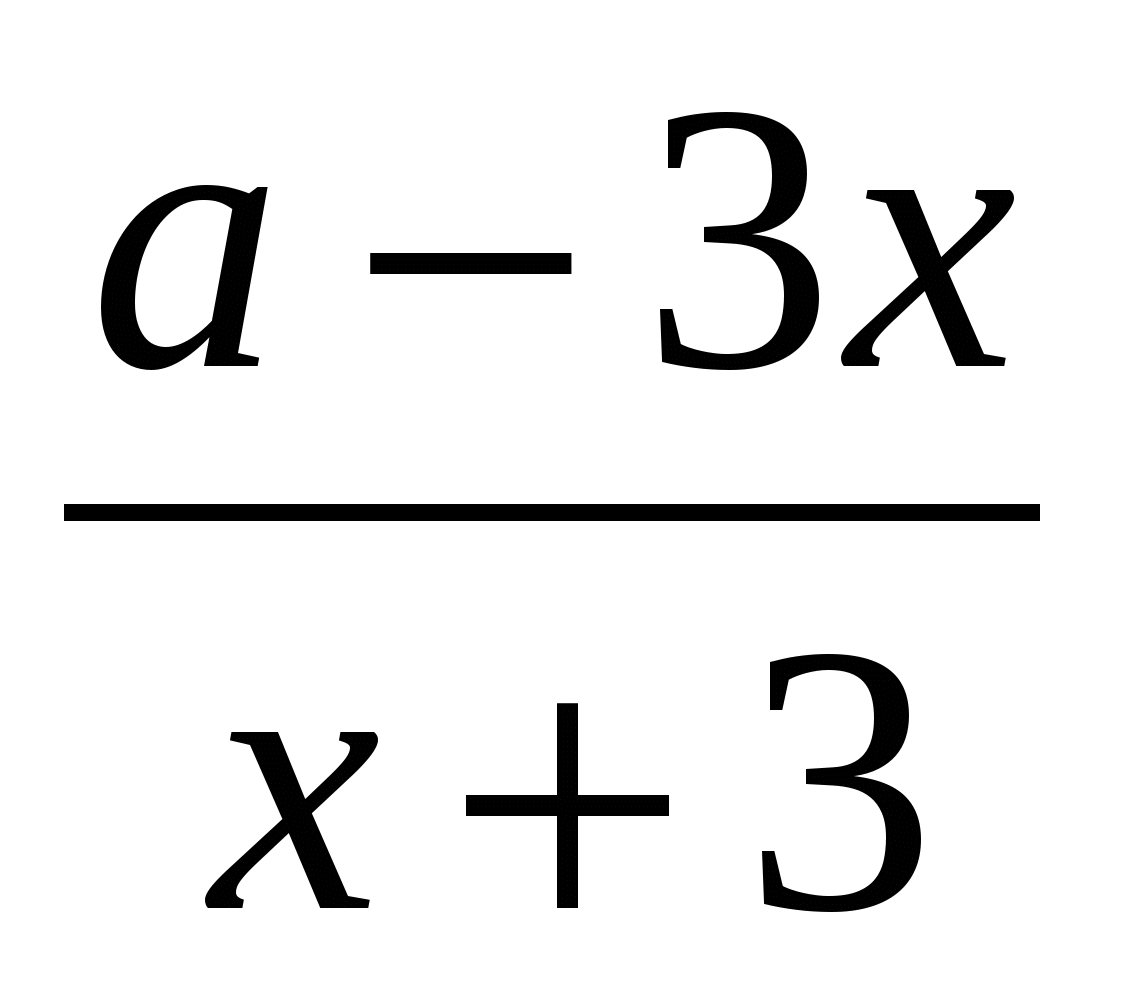 = -2 = -2
|
-9; -5; -1
|
|
5
|
При каких a уравнение имеет единственное решение:
x+2 = a(x-1)
|
(-1;1]
|
|
6
|
При каких a уравнение имеет единственное решение:
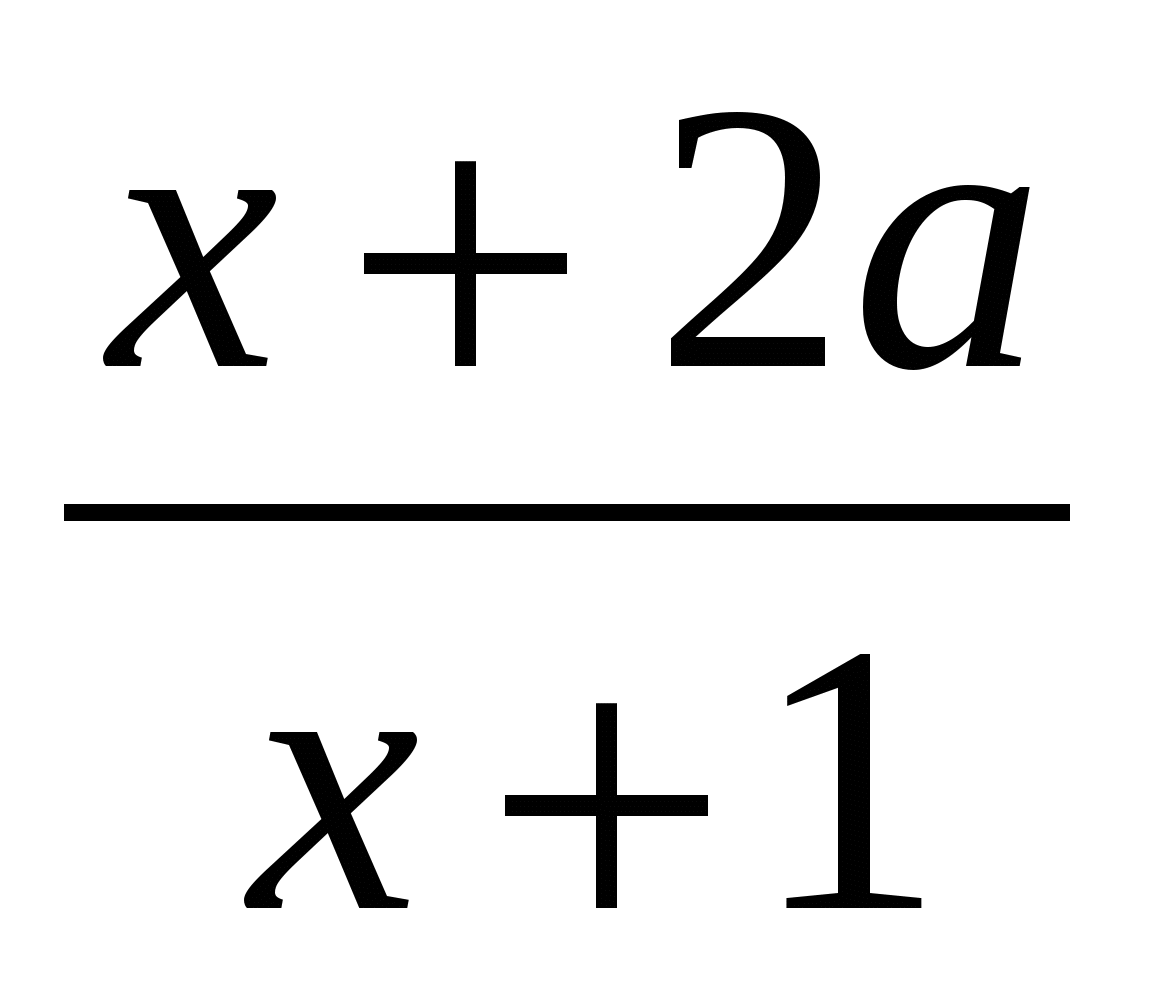 + + 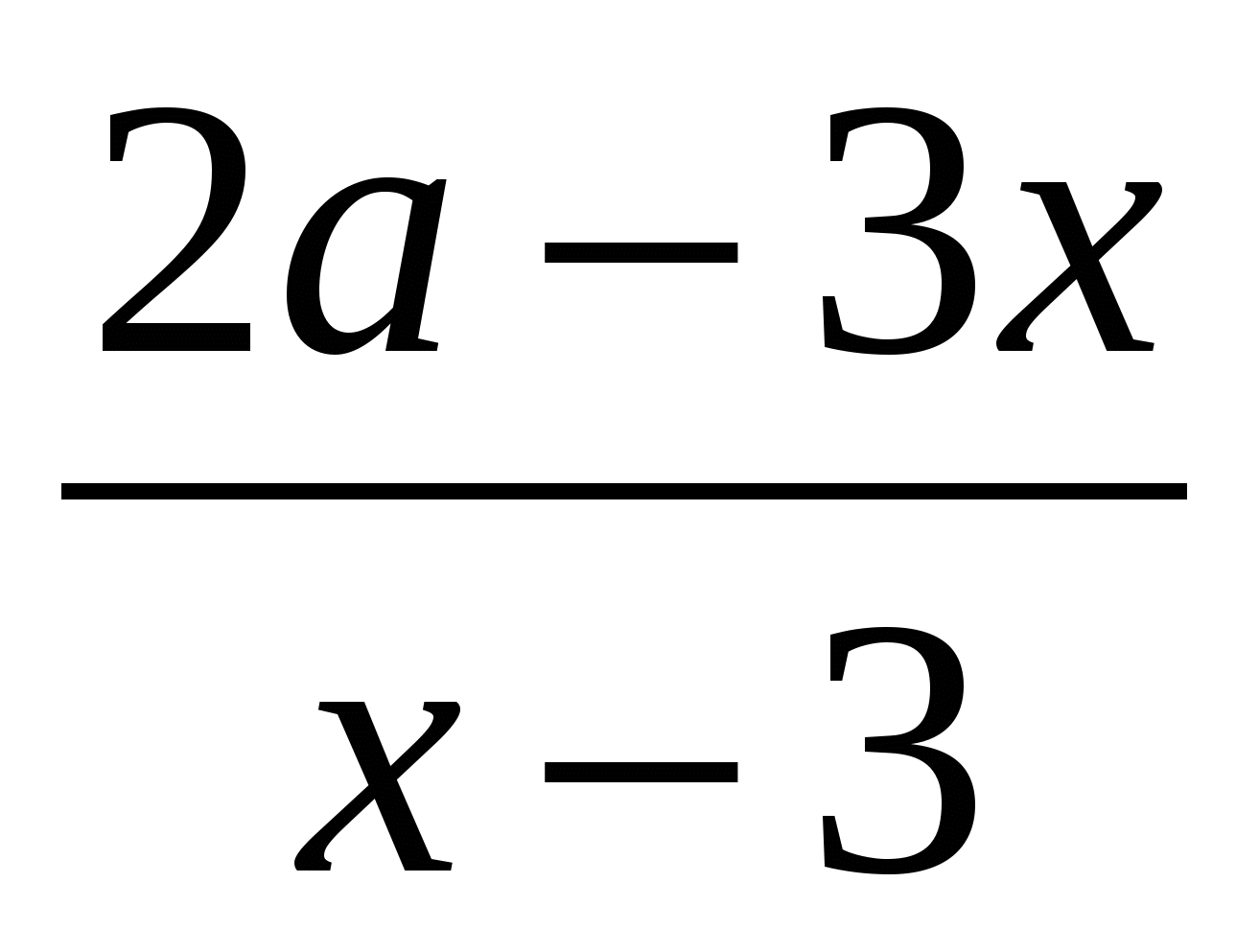 = 2 = 2
|
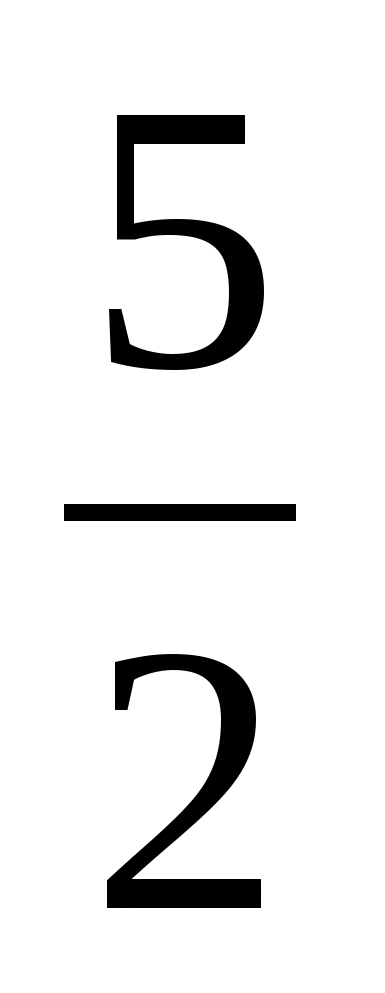 ; ; 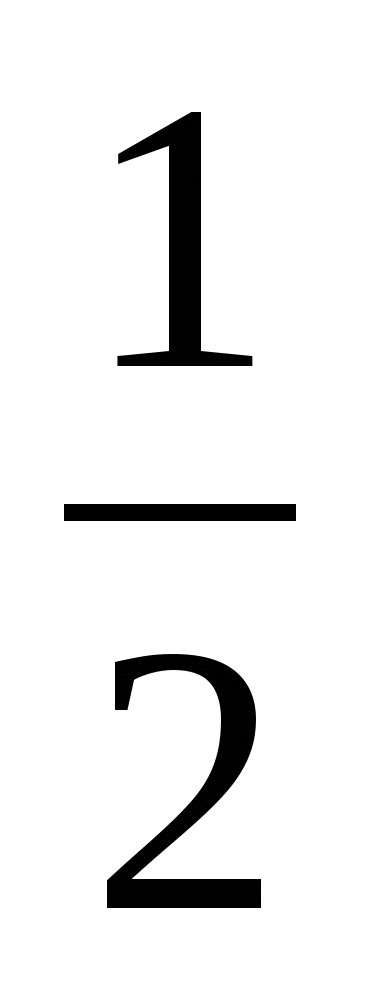 ; ;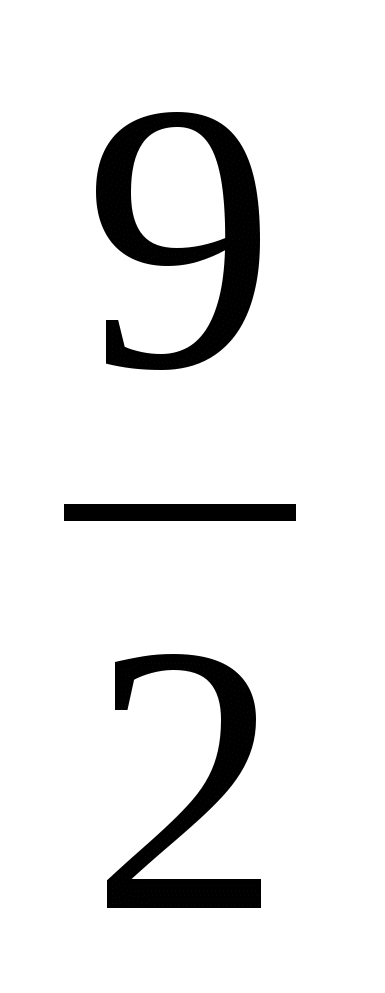
|
|
7
|
При каких a один из корней больше 3, а другой меньше 3.
(a2+a+1)x2 + (a-1)x + a2 = 0
|
Ни при каких a.
|
|
8
|
При каких a все корни уравнения лежат вне отрезка [-1;1]:
a2x2- ax-2 = 0
|
(-1;0)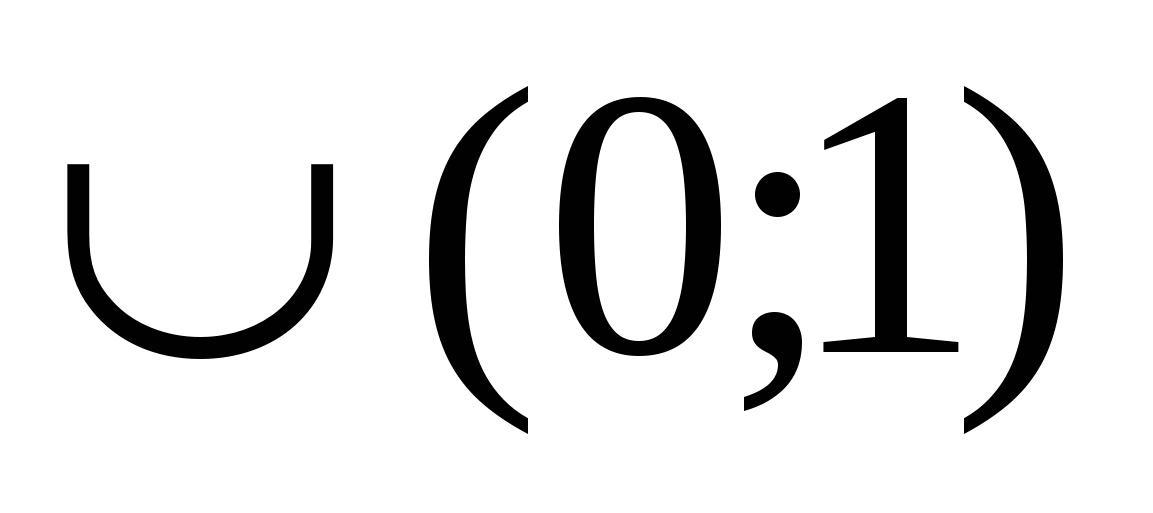
|
|
9
|
При каких a уравнение имеет корни разных знаков.
2x2-( a3+8a-1)x+a2-4 = 0
|
(-2;2)
|
|
10
|
При каких a оба корня уравнения принадлежат отрезку [0;3]:
x2-ax+2 = 0
|
[2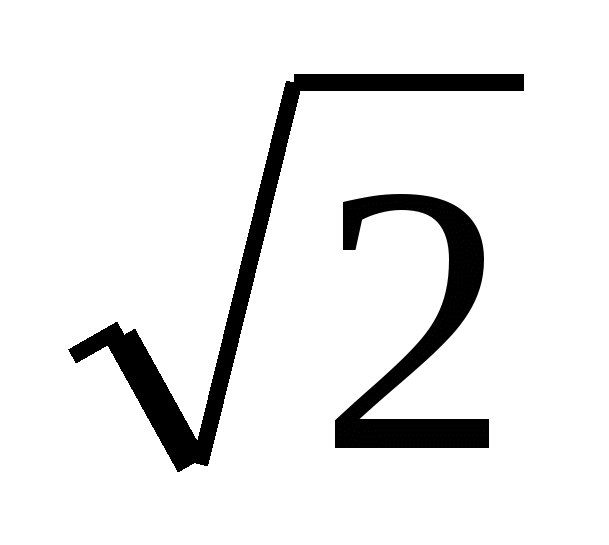 ; ; 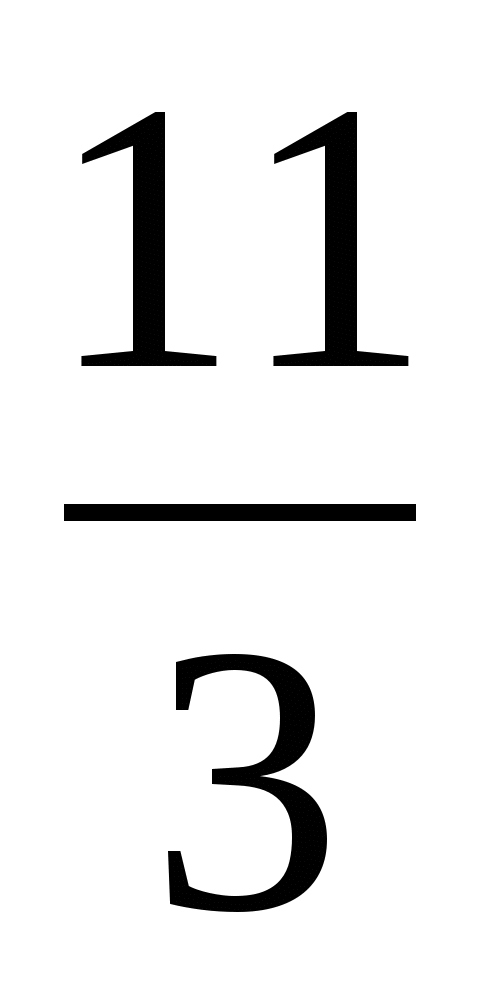 ] ]
|
|
11
|
При каких a больший корень уравнения принадлежит промежутку [0;1):
x2+4x-(a-1)(a-5) = 0
|
(0;1]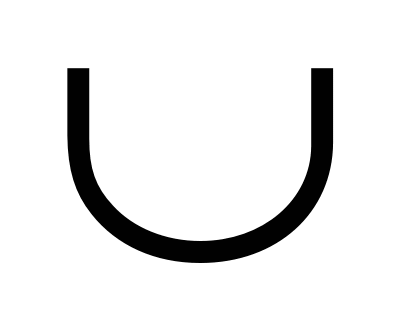 [5;6) [5;6)
|
|
12
|
При каких значениях параметра a уравнение имеет 2 корня:
x4-(5a+6)x2+4a2+6a= 0
|
-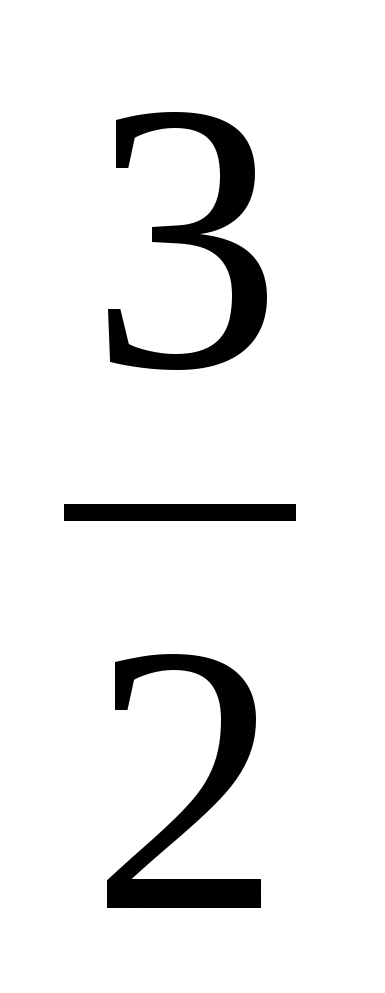 < a < 0 < a < 0
|
|
13
|
При каких значениях параметра a уравнение имеет 4 различных корня:
(x2-2x)2-(a+2)(x2-2x)+3a-3 = 0
|
a >0, a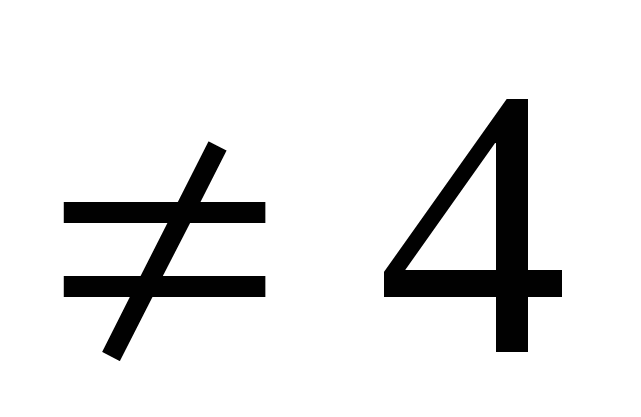
|
|
14
|
При каких a уравнение имеет два корня, причем один из них меньше 1, а другой больше 2:
(a-5)x2-2ax+a-4 = 0
|
(-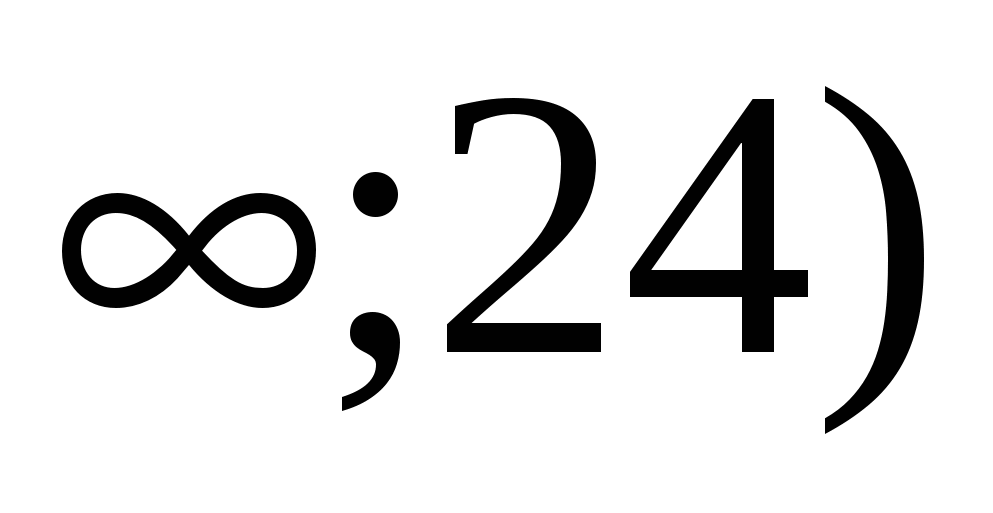
|
|
15
|
При каких a оба корня квадратного уравнения больше 1:
x2-2(a-1)x+a+1 = 0
|
[3;4]
|
|
16
|
При каких a корни уравнения удовлетворяют условию: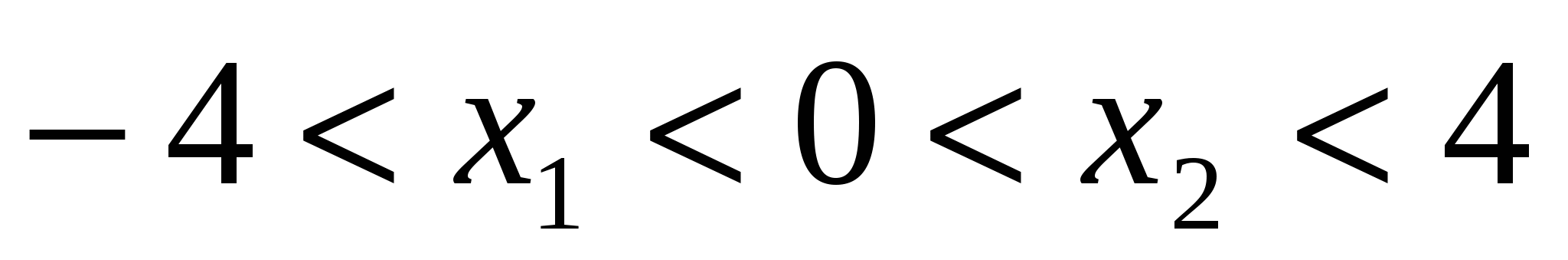
x2-2(a-1)x+2a+1 = 0
|
(-0,9; -0,5)
|
|
17
|
При каких a оба корня квадратного уравнения будут положительны:
(a-2)x2+8x+a+4 = 0
|
[-6;-4]
|
|
18
|
При каких a уравнение не имеет корней:
x4-(a-3)x2+a = 0
|
(0;9)
|
|
19
|
При каких значениях a уравнение имеет более трех решений:
|x2-6x+8| + |x2-6x+5| = a
|
3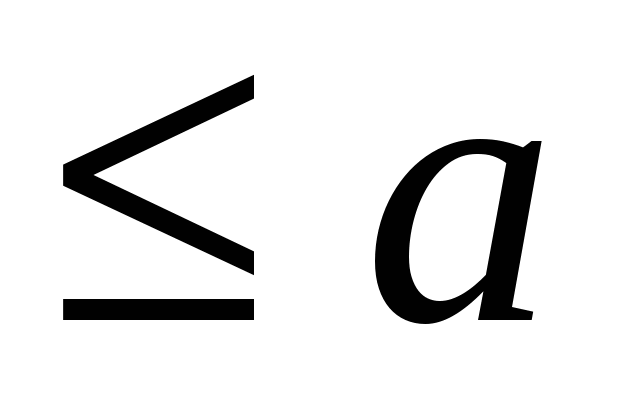 <5 <5
|
|
20
|
При каких a уравнение имеет два различных корня:
x2-2(2a+1)|x| + 3a2+6a = 0
|
(-2;0), a = 1
|
|
21
|
При каких a уравнение имеет бесчисленное множество решений:
|x-6| + |x-3| = a
|
9
|
|
22
|
При каком a уравнение имеет одно решение:
x2+4x-5+(x+2)2 = a
|
-9
|
|
23
|
При каких a уравнение имеет ровно три различных действительных корня:
x2- 6|x| + 5 = a
|
5
|
|
24
|
При каких a квадратное уравнение имеет единственный корень:
x2+(a-2,8)x+|a-2,8| = 0
|
8,4
|
|
25
|
Найти сумму a, при которых уравнение имеет ровно 3 корня:
||x-10|-6| = ax+4
|
-0,05
|
C
|
26
|
При каких a уравнение имеет решения:
a2(2-3|x|)+2a(1-3|x|) = 3|x|
|
(-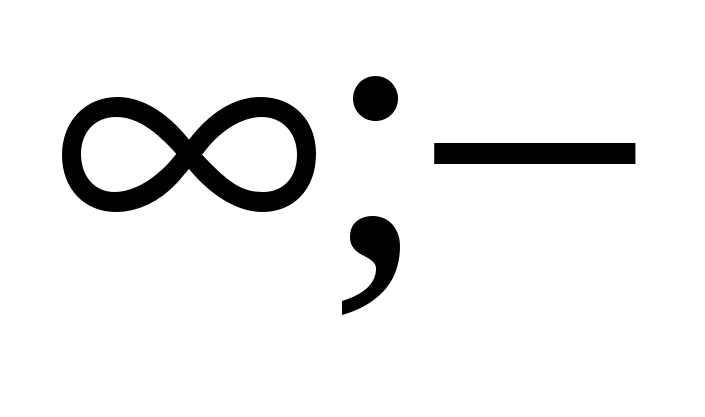 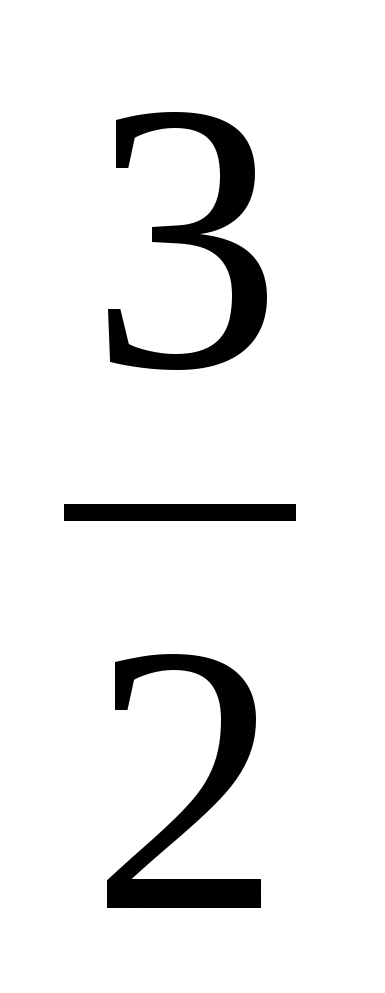 ) )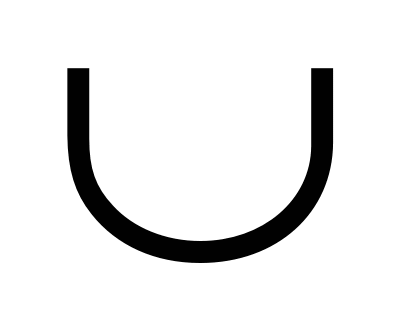 [2;+ [2;+ ) )
|
 Скачать 44.23 Kb.
Скачать 44.23 Kb.