Урок по геометрии в 8 классе с элементами исследовательской деятельности по теме «Четырёхугольники»
 Скачать 0.59 Mb.
|
МОУ «Лямбирская средняя общеобразовательная школа №2» Лямбирского муниципального района Республики Мордовия СБОРНИК МЕТОДИЧЕСКИХ РАЗРАБОТОК из опыта работы учителя математики МОУ «Лямбирская СОШ №2» Одышевой Ольги Валентиновны по применению элементов исследовательской деятельности учащихся на уроках математики в 8-9 классах 2012г. СОДЕРЖАНИЕ
ВВЕДЕНИЕ Изменения, происходящие в современном российском обществе, затрагивают не только идеологическую сферу и экономические основы функционирования государства, они существенным образом касаются и системы общего и профессионального образования. Общество, в котором знания становятся капиталом и главным ресурсом экономического благополучия, предъявляет все более высокие требования как к профессиональной, так и общеобразовательной школе. В общем образовании все больше внимания сосредотачивается на подготовке учащихся к Единому государственному экзамену. На этом фоне уходят на второй план задачи развития творческих способностей учащихся. А ведь именно это ведет к выявлению талантливых детей, что в конечном счете определяет развитие интеллектуального потенциала нашей страны в будущем. `Для того чтобы стремление к приобретению новых знаний не утрачивалось, необходимо воспитывать исследовательскую культуру. Для того чтобы исследовательская деятельность заняла центральное место в построении процесса образования, необходимо создать максимально насыщенную среду, стимулирующую развитие познания. Очевидно, что творческий потенциал учащихся задействован не в полной мере, и это отрицательно сказывается на эффективности учебного процесса. Решение этой проблемы – основное условие достижения нового качества образования по математике. В развитии исследовательской деятельности учащихся в России имеются давние традиции. Главной целью этой деятельности являлась подготовка абитуриентов для вузов. В современных условиях, когда актуален вопрос о снижении учебной нагрузки детей, значение термина «исследовательская деятельность учащихся» приобретает иное значение. В нем уменьшается доля профориентационного компонента, факторов научной новизны исследований, и возрастает содержание, связанное с пониманием исследовательской деятельности как инструмента повышения качества образования. Идеи исследовательского метода обучения получили развитие в трудах ученых Б.П. Есипова, М.А. Данилова, М.Н. Скаткина, И.Я. Лернера. Они указывали, что главным смыслом исследования в сфере образования является то, что оно является учебным. Это означает, что его главной целью является развитие личности, а не получение объективно нового результата, как в «большой» науке. Исследовательский метод определяется как самостоятельное решение учащимися новой для них проблемы с применением таких элементов научного исследования, как наблюдение и самостоятельный анализ фактов, выдвижение гипотезы и ее проверка, формулирование выводов, законов и закономерностей. Однако исследовательский метод обучения охватывает не весь процесс обучения. Ученик не может и не должен усваивать весь объем знаний только путем личного исследования и открытия новых для себя законов, поскольку самостоятельное исследование требует больше времени, чем восприятие объяснения учителя. Проблема состоит в том, чтобы в процессе обучения смоделировать потенциальную исследовательскую деятельность. Еще К. Д. Ушинский категорически отвергал уроки, построенные на основе схематизма и трафарета, не побуждающие ребенка к восприятию и осмыслению изучаемого материала, не вооружающие его навыками и умениями самостоятельной работы, не способствующие развитию его творческого потенциала. Поэтому я считаю, что элементы исследовательской деятельности в той или иной форме должны систематически применяться на уроках, органически сочетаясь с основным содержанием урока. По моему мнению, самый надежный и проверенный способ реализации исследовательского метода на уроках математики – это система познавательных заданий. Познавательное задание – это определенные учебные условия, которые требуют от ученика активизации всех познавательных процессов – мышления, воображения, памяти, внимания и т.д. Поэтому я применяю их на разных этапах урока – при постановке цели, изучении нового материала, его закрепления и для домашних заданий. Осуществляя целенаправленное применение специально подобранных упражнений, я стараюсь учить своих учеников наблюдать, пользоваться аналогией, индукцией, сравнениями, и делать соответствующие выводы. В практике своей работы я широко использую устные упражнения по готовым чертежам. В учебниках по математике мало творческих заданий по рисункам. При работе по готовому чертежу учащиеся из рисунка усматривают свойства фигур, на основе этого делают определённые выводы, а затем доказывают их. Например, учащиеся должны объяснять, почему АВСО является прямоугольником, ТОВЕ – параллелограммом, а МРНК – квадратом, хотя по внешнему виду первые два четырёхугольника «кажутся» квадратами, последний – ромбом (данные обозначены на чертежах). Традиционные формулировки школьных задач по математике, содержащие готовые утверждения, неоправданно сужают пространство выбора. Дело здесь именно в формулировках. Почти всякую школьную задачу на доказательство можно сформулировать так, что в решении появится элемент исследования. Главный подход в том, чтобы ставить задачи разными способами, притом такими, которые дают ученику пространство выбора. Во время фронтального опроса я применяю специальные упражнения, которые требуют от учащихся умения применять определения, теоремы, аксиомы в различных ситуациях, умения быстро ориентироваться в условиях задачи. Любые вопросы типа «Что называется…? Как формулируется такая-то теорема?» легко заменить соответствующими упражнениями. Выполняя их, учащиеся и формулируют, и применяют определения, теоремы, а значит, лучше понимают их. Например, вместо вопроса: «Что называется параллелограммом?» предлагается упражнение: «Какие фигуры на рисунке являются параллелограммами? Данные обозначены на чертежах». При ответе учащиеся не просто воспроизводят определения и теоремы, а осуществляют выбор и учатся их применять. При изучении геометрических понятий в зависимости от характера изучаемого материала, наличия учебного времени, уровня развития учащихся я составляю упражнения таким образом, чтобы учащиеся построили соответствующую фигуру и смогли достаточно быстро выделить те признаки нового понятия, которые необходимы для формулирования определения. Например: 1) Постройте угол. Продлите его сторону за вершину. Вы получили два угла, которые называются смежными. Попытайтесь сформулировать определение смежных углов. Обычно учащиеся быстро улавливают, что для формулирования нового определения достаточно несколько перефразировать упражнение, данное учителем. Но можно и усложнить задание, если дать его в другом виде: 2) Проведите прямую, а затем из любой её точки – луч. Вы получили два угла, которые называются смежными. Попытайтесь сформулировать определение смежных углов. Необходимо учить учащихся умению приводить примеры и контрпримеры к изучаемым понятиям и теоремам. Для активизации мыслительного процесса учащихся и углубления понимания ими понятия «контрпримеров» полезно рассматривать задания на определение ложности и истинности выражений, на отыскание ошибок в формулировках утверждений. Исследование – это творчество. Заставить творить нельзя. Поэтому исследование не поддаётся формализации – и в обучении и в проверке. Как оценивать исследовательские умения? Лучше всего избегать формальных оценок, потому что этим умениям нельзя гарантированно научить, а значит, нельзя их и уравнивать. Если ученик несколько раз успешно находил требуемое на уроках, то это совсем не значит, что в новой ситуации он это тоже найдёт. Оценивать можно базовые знания, полученные учащимися на основе применения элементов исследовательской деятельности через познавательные задания. Подводя итог, могу сказать, что исследовательский метод позволяет активизировать мыслительную деятельность учащихся, повысить их интерес, и приводит к хорошему усвоению материала, к развитию мышления и способностей учащихся. В то же время этому методу присущи следующие недостатки: 1) он требует большей, чем при сообщении готовых знаний, затраты времени; 2) при этом методе особенно сильно сказываются индивидуальные различия учащихся; 3) активное участие в решении проблемы или в беседе принимают лишь отдельные учащиеся, остальные – пассивны. Поэтому исследовательский метод следует использовать в разумной мере, нейтрализуя его недостатки с помощью различных приёмов. Прежде всего нужно помочь тем учащимся, которые не успевают решать на уроках поставленной проблемы. На уроке ставятся нетрудоёмкие проблемы, которые успевают решить все учащиеся класса с небольшой разницей во времени. Более трудоёмкие проблемы можно включать в домашние задания. В этом случае на уроке только создаётся проблемная ситуация и ставится проблема. Тогда в домашних условиях каждый ученик может спокойно, не торопясь, рассмотреть достаточное число частных случаев, обратиться к книгам и самостоятельно прийти к «открытию», испытывая при этом большое удовлетворение, что обычно проявляется на следующий день в оживлённых дискуссиях. Все вышеприведённые и рассмотренные примеры использования элементов исследовательской деятельности учащихся на уроках математики, выводы и обобщения являются результатом моей работы по данной теме в течение четырёх лет. Думаю, что опыт моей работы может пригодиться многим учителям, применяющим технологии проектной и исследовательской деятельности учащихся. Поэтому предлагаю некоторые свои методические разработки к урокам геометрии в 8 классе по использованию элементов исследовательской деятельности учащихся на уроках математики. 1. Устные задания на повторение и закрепление пройденного материала с элементами исследовательской работы на тему «Четырёхугольники», 8 класс. 1. Прочитайте в учебнике определение прямоугольника и установите, можно ли его видоизменить таким образом: «Параллелограмм, у которого есть прямой угол, называется прямоугольником». 2. В четырёхугольнике AВCK стороны AB и CK равны, а стороны BC и AK параллельны, ВС = 4 см. Если можно, вычислить АК. (Ответ: вычислить нельзя, т.к. по условию AВCK может быть или параллелограммом, или трапецией, и нельзя применить теорему: «Если две стороны четырёхугольника равны и параллельны, то он является параллелограммом». Здесь по условию две стороны равны, а две другие стороны параллельны.) 3  . Какие фигуры на рисунке являются параллелограммами? Найти длину ВК. (Данные обозначены на чертежах.)  4  . Объяснить, почему АВСО является прямоугольником, ТОВЕ – параллелограммом, а МРНК – квадратом. 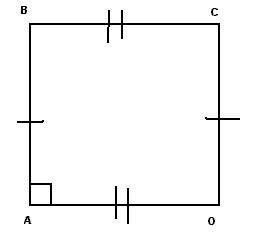 5. Перечислите свойства, которыми обладают отрезки АВ и СК. Данные обозначены на чертежах. (Чертежи вывешиваются последовательно один за другим.)     6. Указать вид четырёхугольников. Данные указаны на чертежах.       7. Какие фигуры изображены на следующих чертежах? Данные обозначены на чертеже.         8  . Назовите оси и центры симметрии следующих фигур (данные обозначены на чертежах).     9. Установите истинность или ложность следующих высказываний:
2. Обобщающий урок по геометрии в 8 классе с элементами исследовательской деятельности по теме «Четырёхугольники», геометрия, 8 класс. Цели:  обобщить и систематизировать знания учащихся по изученной теме; закрепить умения применять полученные знания; совершенствовать навыки решения задач; проверить качество усвоения геометрического материала, готовность ученика использовать полученные знания и умения при решении нестандартных и исследовательских задач; развивать навыки логического мышления и исследовательской деятельности; развивать математическую речь учащихся.Оборудование: задачи на готовых чертежах; дидактические карточки-задания; таблица свойств четырёхугольников; тесты в 4-х вариантах. |