Урок по геометрии в 8 классе с элементами исследовательской деятельности по теме «Четырёхугольники»
 Скачать 0.59 Mb. Скачать 0.59 Mb.
|
Ход урока1. Организационный момент. Сообщить тему урока, сформулировать цели урока. 2. Актуализация знаний учащихся. Устная работа на повторение изученного материала. 1) Работа по таблицам свойств четырёхугольников по цепочке с комментированием. Задание: установите истинность или ложность следующих высказываний, отметив знаки «+»(истинно) или «-» (ложно).
2) Решение задач на готовых чертежах (устно): В С а) ABCD – прямоугольник. 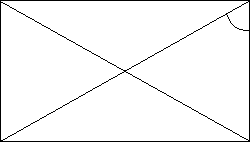 Найти: АОВ, ВОС. Найти: АОВ, ВОС. 60 О А D В С 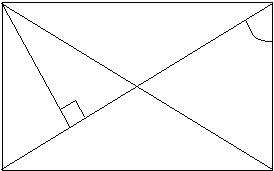 О б) ABCD –прямоугольник. 60 Найти: АС, АВ. А D Е 3. Решение задач. 1) Задачи на построение, выполняемые на клетчатой бумаге (групповая форма работы). Каждая группа доказывает своё решение у доски. 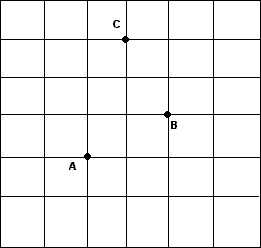 а) Постройте параллелограмм, тремя вершинами которого являются точки А, В, С, а вершина D находится в узле сетки. Сколько решений имеет задача? 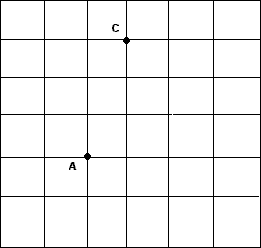 б) Постройте прямоугольник, диагональю которого является отрезок АС, а вершины В и D находятся в узлах сетки. Сколько решений имеет задача? 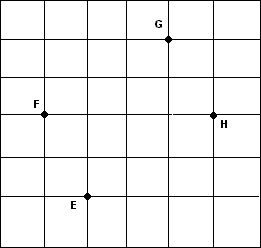 в) Постройте параллелограмм, серединами сторон которого являются точки E, F, G, H. 2) Задача – исследование. Каким четырёхугольником будет являться фигура, вершины которой находятся в серединах сторон прямоугольника? Постройте эту фигуру и докажите полученный при построении результат. 4. Проверка качества усвоения материала. ТЕСТВ-1 1. Центр симметрии имеет буква: а) А; б) М; в) Х; г) К. 2. Окружность имеет осей симметрии: а) 1; б) 2; в) 3; г) бесконечно много. 3. Углы при основании трапеции равны 71 и 34. Тогда остальные углы трапеции будут равны: а) 34 и 71; б) 56 и 19; в) 105 и 75; г) 109 и 146. 4. В равностороннем треугольнике с длиной стороны, равной 18 см, через середину одной из них проведены прямые, параллельные двум другим сторонам треугольника. Тогда периметр образовавшегося четырёхугольника будет равен ___________________. 5. Углы в параллелограмме ABCD С = 60, В = 120. Тогда D равен ________________. В-2 1. Прямоугольник имеет осей симметрии: а) 1; б) 2; в) 3; г) 4. 2. Прямая имеет осей симметрии: а) 0; б) 1; в) 2; г) 3. 3. В трапеции ABCD диагональ острого угла А является биссектрисой данного угла. Тогда АВС является: а) равнобедренным тупоугольным; б) равнобедренным прямоугольным; в) равносторонним; г) разносторонним. 4. Периметр квадрата MNKL равен 24 см. Тогда сторона квадрата MN равна ____________. 5. В ромбе перпендикуляр, проведённый из вершины тупого угла к стороне ромба, делит эту сторону пополам. Тогда углы ромба будут равны ______________________________. В-3 1. Отрезок имеет осей симметрии: а) 0; б) 1; в) 2; г) бесконечно много. 2. Ромб, не являющийся квадратом, имеет осей симметрии: а) 0; б) 1; в) 2; г) 4. 3. В прямоугольнике перпендикуляры, проведённые из точки пересечения диагоналей к его сторонам, равны соответственно 3 см и 5 см. Тогда периметр прямоугольника будет равен: а) 16 см; б) 24 см; в) 48 см; г) 32 см. 4. Периметр ромба ABCD равен 20 см. Тогда сторона ромба равна _________________. 5. В трапеции три стороны равны 4 см, а четвёртая – 8 см. Тогда наибольший угол трапеции равен __________________. В-4 1. Квадрат имеет осей симметрии: а) 1; б) 1; в) 2; г) 4. 2. Ось симметрии имеет буква: а) А; б) Г; в) F; г) L. 3. В равнобедренной трапеции основания равны 13 см и 28 см, острый угол равен 60. Тогда периметр трапеции равен: а) 41 см; б) 71 см; в) 82 см; г) 20,5 см. 4. Острый угол ВАD ромба ABCD равен 72. Тогда DBC равен _______________. 5. В прямоугольнике один из углов, образованных диагоналями, равен 120. Диагонали прямоугольника равны 18 см. Тогда меньшая сторона прямоугольника равна ___________. 5. Итоги урока. Домашнее задание. Задачи-исследования:
3. Урок с применением ИКТ с использованием элементов исследовательской деятельности учащихся «Касательная к окружности. Центральный и вписанный угол», геометрия, 8 класс. Тип урока: обобщение и систематизация знаний; контроль усвоения знаний и умений. Вид урока: урок – исследование. ЦЕЛИ:
1. ученик должен знать: - употребляемые термины: радиус, диаметр, хорда, дуга окружности, полуокружность, градусная мера дуги окружности; - определение окружности, касательной к окружности, центрального и вписанного углов, свойство и признак касательной; 2. ученик должен понимать: - как определять взаимное расположение окружности и прямой на плоскости; - как находить градусную меру дуги окружности; 3. ученик должен уметь: - определять по рисунку центральный и вписанный углы; - определять по рисунку и изображать касательную к окружности; - применять свойства и следствия изученных теорем;
Оборудование: ИТ – презентация; тест; лист самооценки. ПЛАН УРОКА:
ХОД УРОКА: 2. Проверка домашнего задания. Задача № 660. Через точку, лежащую вне окружности, проведены две секущие, образующие угол в 32. Большая дуга окружности, заключённая между сторонами этого угла, равна 100. Найдите меньшую дугу. Р 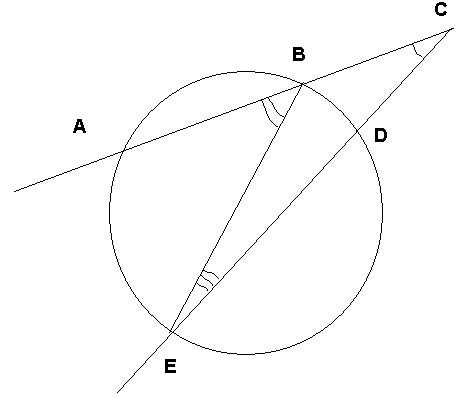 ешение. ешение.
то АВЕ =
то АВЕ = ВЕС + BCD, откуда ВЕС = АВЕ - BCD, ВЕС = 50 – 32 = 18.
то ВЕD = то BD = 2 ВЕD = 2 18 = 36. Ответ: BD = 36. 3. Устная работа на повторение. 1) Найти ошибку в утверждении и придумать контрпример (показать на доске и слайдах):
2) Решение задач по готовым чертежам (слайды презентации): 1. Ответ: х = 60. 2. Ответ: х = 80. 3. Ответ:АВС = 360 - 80 = 280; х = 280 : 2 = 140. 4. Ответ:ВА = 360 - 110 = 250; х = 250 : 2 = 125. 5. Ответ:С = 90; А = 90 - 37 = 53. 6. Ответ:х = (60 + 180) : 2 = 120. 4. Зрительный математический диктант с взаимопроверкой (слайды презентации). Вставьте пропущенное слово, число или формулу, чтобы получилось верное высказывание: В - 1
В – 2
Ответы: (на слайде)
5. Решение задач с применением элементов исследовательской деятельности. 1) Вывод и доказательство утверждения о величине угла между двумя секущими. Вернёмся к домашней задаче: (рисунок на слайде) Заметим, что (100 – 36) : 2 = 64 : 2 = 32. Наводящие вопросы:
Гипотеза: 1)Угол между двумя секущими, проведенными из одной точки, равен полуразности большей и меньшей дуг, заключенных между его сторонами. 2)Угол, вершина которого лежит вне круга и стороны пересекаются с окружностью, измеряется полуразностью большей и меньшей дуг, заключенных между его сторонами. Т.е., нам надо доказать, что АСЕ = Доказательство:
АВЕ = ВЕС + ВСЕ, ВСЕ = АВЕ - ВЕС, ВСЕ = Применение: №661 (устно). Решение: = (140 – 52) : 2 = 88 : 2 = 44. 2 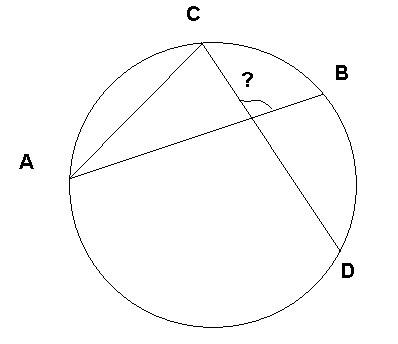 ) Вывод и доказательство утверждения о величине угла между двумя пересекающимися хордами. ) Вывод и доказательство утверждения о величине угла между двумя пересекающимися хордами.Рассмотрим две пересекающиеся хорды окружности (слайд). Наводящие вопросы: 1. Являются ли центральными или вписанными углы, образованные пересекающимися хордами? 2. Проведём хорду АС. Какие вписанные углы при этом получились? 3. Рассмотрим вписанные углы АСD и САВ: АСD = 4. Неизвестный угол - внешний угол АСЕ, значит его величина равна сумме двух других углов треугольника, не смежных с ним: = АСD + САВ = 5. Сформулируйте гипотезу о величине угла между двумя пересекающимися хордами. Гипотеза: Угол между двумя пересекающимися хордами равен полусумме двух дуг, заключённых между этими хордами. Применение: №662 (устно). Решение: = (54 + 70) : 2 = 124 : 2 = 64. 6. Упражнения для разгрузки и снятия напряжения с глаз и мышц спины и шеи
7. Тест по теме «Касательная к окружности. Центральные и вписанные углы» Ответы:
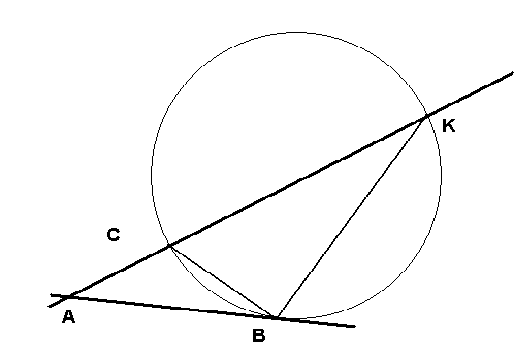 8. Домашнее задание. №664; №670. Задача №670. Прямая АВ касается окружности в точке В. Прямая АР пересекает её в точках С и К. Доказать, что АВ2 = АК АС. (1) Указания. 1. Т.к. равенство (1) следует из пропорции 2. Т.к. АВС и АВК имеют общий угол А, то необходимо доказать, что ВКС = АВС. 3. Обратить внимание, что ВКС – вписанный. 4. Т.к. АВС составлен касательной и хордой, применить теорему об измерении угла между касательной и хордой (№664). Итоги урока:
Лист самооценки
4. Урок с применением ИКТ, ЭУМ, с использованием элементов исследовательской деятельности учащихся «Площадь многоугольников. Теорема Пифагора», геометрия, 8 класс. Тема и номер урока в теме: глава VI. Площадь (13 ч), урок №12. Тип урока: обобщение и систематизация знаний по темам «Площадь многоугольников», «Теорема Пифагора». Вид урока: комбинированный урок с элементами исследовательской деятельности учащихся. Формы работы учащихся: групповые и индивидуальные, работа в парах, элементы исследовательской деятельности. Необходимое техническое оборудование: компьютерный класс с мультимедийным проектором, ПК, презентация, интерактивная доска. Цель: систематизировать и обобщить знания учащихся по изученным темам. Задачи: - обучающие: систематизация и обобщение изученного материала и его применение в стандартных условиях; перенос приобретенных знаний в новые или измененные условия с целью формирования умений использовать полученные знания и умения для решения нестандартных и исследовательских задач; мотивация учебной деятельности через осознание учащимися практической значимости применяемых знаний и умений; проверка качества освоения необходимого геометрического материала и готовности учеников применять его в необычной ситуации; создание разноуровневых условий контроля (самоконтроля, взаимоконтроля) усвоения знаний и умений: 1. ученик должен знать: - употребляемые термины: понятие площади многоугольника; единицы измерения площадей; определения прямоугольника, параллелограмма, ромба, треугольника, трапеции; формулировки теоремы Пифагора и теоремы, обратной теореме Пифагора; - формулы площадей прямоугольника, параллелограмма, ромба, треугольника, трапеции; свойства площадей многоугольников; 2. ученик должен понимать: - как измерить и вычислить площадь многоугольника; - классификацию, логические обоснования, доказательства математических утверждений, касающихся понятия площадь; 3. ученик должен уметь: - формулировать основные свойства площадей, теорему об отношении площадей треугольников, имеющих по равному углу; формулировать теорему Пифагора и обратную ей; - решать задачи на вычисление и доказательство, связанные с формулами площадей и теоремой Пифагора; - работать с геометрическим текстом и рисунком (анализировать, извлекать необходимую информацию); - применять изученные понятия, результаты, методы для решения задач практического характера и задач из смежных дисциплин с использованием при необходимости справочных материалов, калькулятора, компьютера; - развивающие: способствовать формированию умений применять полученные знания в новой ситуации, развивать осознание необходимости самостоятельных действий при решении некоторых проблем; развивать математическое мышление, речь, геометрические представления учащихся; способствовать выработке необходимых вычислительных навыков и практических умений; помочь учащимся преодолеть психологический барьер и поверить в свои силы; -воспитательные: стимулировать учащихся к самооценке образовательной деятельности; совершенствовать культуру труда; воспитывать культуру личности, отношение к геометрии как к части общечеловеческой культуры, понимание значимости геометрии для научно - технического прогресса; содействовать воспитанию интереса к математике, активности, мобильности, умения общаться. ПЛАН УРОКА
с целью формирования умений использовать полученные знания и умения для решения нестандартных и исследовательских задач.
( 7 мин )
( 2 мин ) ХОД УРОКА
Ребята, мы закончили с вами изучение главы VI «Площадь», и сегодня цель нашего урока повторить, систематизировать и обобщить весь изученный материал и постараться ответить на вопрос: где нам могут понадобиться эти знания? Они важны при решении множества геометрических задач и являются базой изучения теоретического материала в дальнейшем. В ходе урока вы сможете убедиться, что геометрия очень важная наука, имеющая огромное практическое применение. Сегодня вы будете выполнять различные задания, а результаты заносить в лист контроля. Один правильный ответ на вопрос – один балл. В конце урока по количеству набранных баллов каждый из вас получит соответствующую отметку. (Приложение №1) На нашем уроке сегодня вы будете участвовать в исследовательской работе, для этого необходимо класс разделить на группы (класс делится на 4 группы по 6 человек дифференцированно с учётом уровня знаний учащихся). Учащиеся записывают в тетрадях число и тему урока.
2.1. Взаимопроверка в парах по слайдам презентации. Проверка домашнего задания проводится в парах в форме взаимопроверки по рабочим тетрадям. Каждый ученик сверяет решение с верным по слайду презентации. Результаты проверки заносятся в листы контроля.
Группе учащихся было дано индивидуальное домашнее задание: подготовить материал о применении теоремы Пифагора в практической деятельности человека. К своим докладам они также подготовили презентацию. Давайте послушаем, какую информацию нам подготовили ребята. (авторская презентация учащихся, Приложение №2) 1) Доклад - исследование учащихся по теме «Применение теоремы Пифагора в архитектуре и строительстве», «Танграм. Паркетостроение». 2) Доклад - исследование учащихся по теме «Пифагоровы тройки». В каких профессиях важны знания по геометрии? (Беседа учителя о некоторых профессиях и о профессиональном выборе). Ребята, как вы думаете, от чего зависит профессиональный выбор каждого человека? (Ученикам раздаются буклеты о профессиях, для которых важны знания по геометрии. В них перечисляются некоторые профессии, содержание их деятельности, требования к профессионально важным качествам и профессиональные знания и умения, зависящие от знаний геометрии, а так же указаны адреса и наименования учебных заведений г.Саранска и Республики Мордовия, в которых можно получить эти профессии. Опираясь на материал этих буклетов учитель ведёт беседу с учащимися. (Приложение №3) Наверное, он зависит: · от возможностей каждого (его способностей, трудолюбия, внимательности, сообразительности, темперамента и т. д.); · от интересов и склонностей; · от требований профессии к личности; · от возможностей родителей; · от востребованности профессии на рынке труда. Очень скоро, через год, и вам тоже предстоит сделать свой выбор: продолжить своё обучение в 10 классе или выбрать профессию по душе и пойти учиться в профлицеи или колледжи. Как вы думаете, ребята, в каких профессиях важны знания по геометрии? (Например, архитектор, строитель, токарь). А сейчас хорошие знания геометрии нам нужны, чтобы уметь применять их при решении задач. Ребята, обратите внимание! В качестве эпиграфа к сегодняшнему уроку я выбрала слова одного из авторов журнала «Квант», известного автора – составителя олимпиадных задач по математике В. Произволова: «Геометрия полна приключений, потому что за каждой задачей скрывается приключение мысли. Решить задачу – это значит пережить приключение» (слайд №2). И я предлагаю вам сегодня дать простор вашим мыслям, чтобы мы все вместе смогли пережить это удивительное приключение.
Ребята, представьте себя на месте учителя. Какие вопросы вы бы задали своим ученикам, чтобы узнать, как они усвоили тему «Четырехугольники», «Площадь многоугольника», «Теорема Пифагора»? Эти вопросы сейчас вы будете задавать друг другу по очереди, а начну первой я сама. Сидящему с края ученику каждой группы учитель задает теоретический вопрос по изученным темам (например, сформулируй теорему о площади параллелограмма, или, что такое площадь), ответив на который, ученик задаёт вопрос сидящему рядом и т. д. по кругу. Вопросы при этом не должны повторяться. Если ученик не ответил на поставленный вопрос, то он переходит к следующему ученику. Ответы учащихся фиксируются в бланке ответов: в соответствующей графе ставится знак «+», либо знак « - ».
Учащиеся устно отвечают на поставленные учителем вопросы, опираясь на иллюстрацию презентации, записывая или изображая решение на слайдах в режиме интерактивной доски; устно исправляют друг у друга ошибки и корректируют ответы.
Дополнительный вопрос по ходу ответов на первый случай: как называется треугольник со сторонами 3, 4 и 5? (египетский треугольник, священный треугольник).
 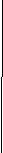  1 2 Решение: 4. Предварительный контроль усвоения материала (с использованием ЭУМ). Тест. Самостоятельная тестовая работа учащихся в парах на ПК с интерактивными заданиями (контрольный ЭУМ по теме «Площадь многоугольников», ПК, 81-КВ.oms, приложение №4), при этом они имеют возможность обсуждать решения друг с другом и консультироваться с учителем. Учитель руководит деятельностью учащихся по работе с ЭУМ: по ходу выполнения учащимися тестовой работы он консультирует учащихся и анализирует уровень усвоения ими изученного материала, отмечая моменты, на которые затем при отработке навыков надо ещё раз обратить особое внимание учащихся. Решения учащихся в тетрадях не фиксируются. - Ребята, после выполнения всех заданий теста посмотрите статистику и заполните лист контроля. 5. Решение задач на применение изученного материала.
А теперь решим задачи на применение свойств площадей многоугольников по заданиям ЭУМ, решения которых будем записывать на доске и в тетрадях (приложение №5). Воспользуемся задачами из заданий Электронного учебного модуля по теме «Площадь многоугольников» (задания демонстрируются для всего класса на экране). Какой теоремой о площадях двух треугольников мы можем сейчас воспользоваться? Сформулируйте эту теорему и примените её для решения предложенных задач. Участие в решении задач также оценивается в листах контроля.
Сейчас – зима, за окном идёт снег. А давайте закроем глаза и представим, что сейчас – лето, мы с вами в лесу, на цветущей поляне, где поют птицы. Свободно откиньте голову назад и сделайте глубокий вдох. Наклоните голову вправо и одновременно приподнимите правое плечо, затем – левое (2-3 раза). Теперь наклоните голову вперёд и одновременно сделайте круговые вращательные движения плечами вперёд и назад (2-3 раза). 1. Упражнения для разгрузки и снятия напряжения с глаз:
2. Упражнения для разгрузки и снятия напряжения с мышц спины и шеи:
5.3. Перенос приобретенных знаний в новые или измененные условия с целью формирования умений использовать полученные знания и умения для решения нестандартных и исследовательских задач.
Пользуясь теоремами об отношении площадей двух треугольников часто бывает удобно сравнивать площади треугольников. Рассмотрим некоторые очевидные, но важные следствия из теоремы. 1) Воспользуемся средствами программы «Живая геометрия» и смоделируем следующую ситуацию: построим произвольный треугольник; через одну из вершин треугольника проведём прямую, параллельную противоположной стороне этого треугольника. Средства программы позволяют двигать указанную вершину треугольника вдоль построенной прямой. 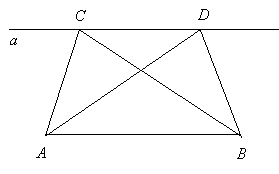 Наводящие вопросы учителя: 1) Что вы можете сказать о полученных треугольниках? (При этом получается множество треугольников с одним и тем же основанием и равными высотами.) 2) Какой теоремой о площадях двух треугольников мы можем воспользоваться для их сравнения? (Теоремой об отношении площадей двух треугольников с равными высотами.)
Гипотеза: Если вершину треугольника передвигать по прямой, параллельной её основанию, то его площадь при этом не меняется. Доказательство: Треугольники АВС и АВD имеют общее основание АВ и равные высоты, опущенные на это основание, т. к. прямая а, которая содержит вершины С и D параллельна основанию АВ, а поэтому площади этих треугольников равны. (слайд №9) 2) Воспользуемся средствами программы «Живая геометрия» и смоделируем следующую ситуацию: построим произвольный треугольник; через одну из сторон треугольника проведём прямую. Средства программы позволяют двигать одну из вершин треугольника вдоль построенной прямой.  Наводящие вопросы учителя: 1) Что вы можете сказать о полученных треугольниках? (При этом получается множество треугольников с одной и той же высотой, основания которых лежат на одной прямой и являются частью друг друга.) 2) Какой теоремой о площадях двух треугольников мы можем воспользоваться для их сравнения? (Теоремой об отношении площадей двух треугольников с равными высотами.) 3) Какое предположение из рассмотренной ситуации мы можем сделать? Гипотеза: Если одну из сторон треугольника, прилежащих к данному его углу, увеличить в k раз, то площадь его также увеличится в k раз. Доказательство: На рисунке треугольники АВС и ABD имеют общую высоту ВH, поэтому отношение их площадей равно отношению оснований. (слайд №10) Участие в исследовательской работе также оценивается в листах контроля.
Определение площадей геометрических фигур – одна из древнейших практических задач. Правильный подход к их решению был найден не сразу, но уже древние греки умели правильно находить площади многоугольников. Давайте ещё раз вспомним, что же такое площадь многоугольника? Площадь фигуры - это число, показывающее, сколько раз единичный квадрат и его части укладываются в данной фигуре. Воспользуемся этим определением для решения следующих задач в групповой форме: найти площадь фигуры, изображённой на клетчатой бумаге. С помощью единичной клетки вы можете найти длины отрезков, необходимых для вычисления площади, вы можете делить фигуру на части, можете применять теорему Пифагора. (слайд №11) (Эти задачи отличаются от обычных задач из учебника по геометрии, и в то же время они не требуют дополнительных сведений. Каждое предложенное задание требует применения геометрических знаний в необычной ситуации.)
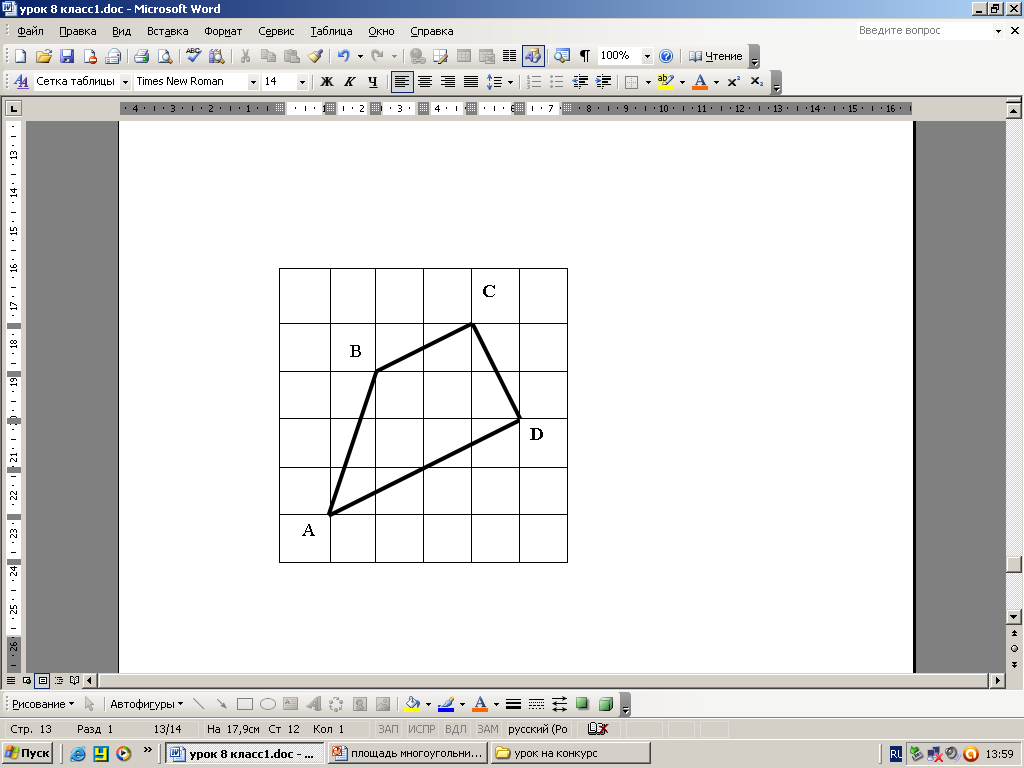
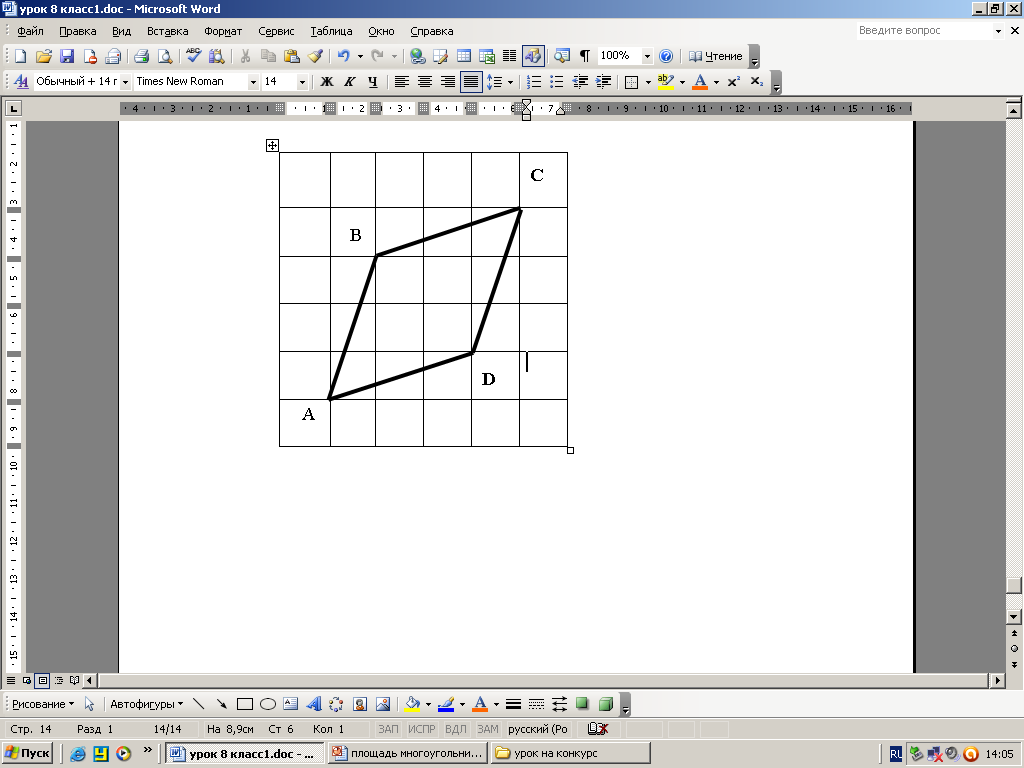
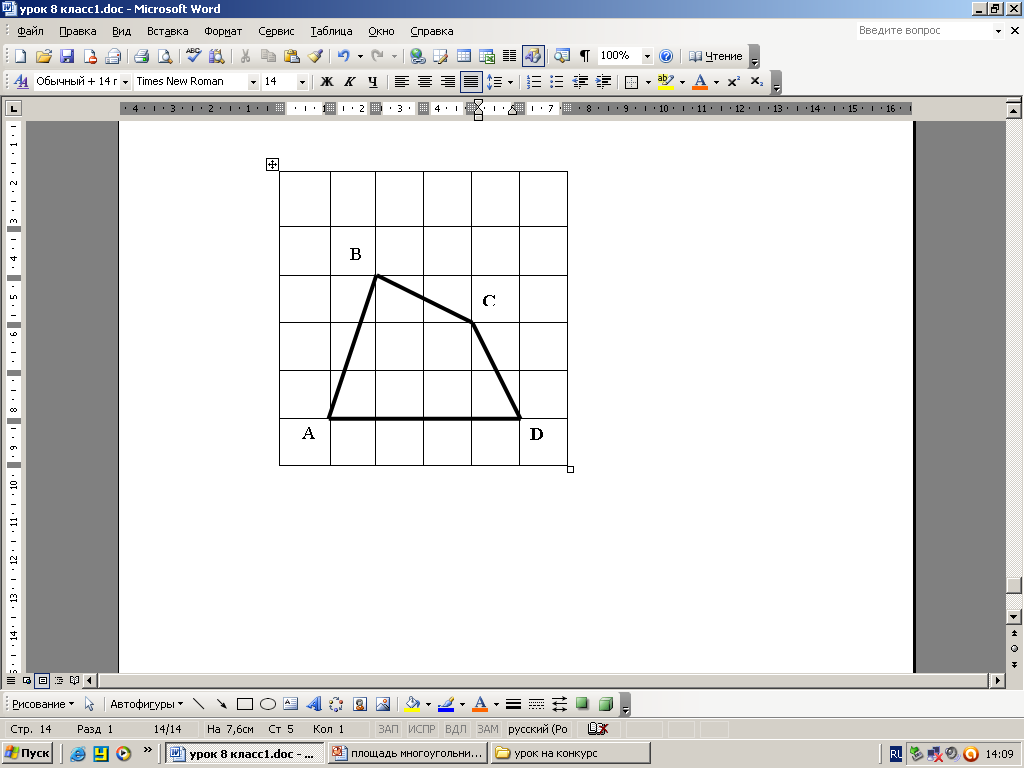
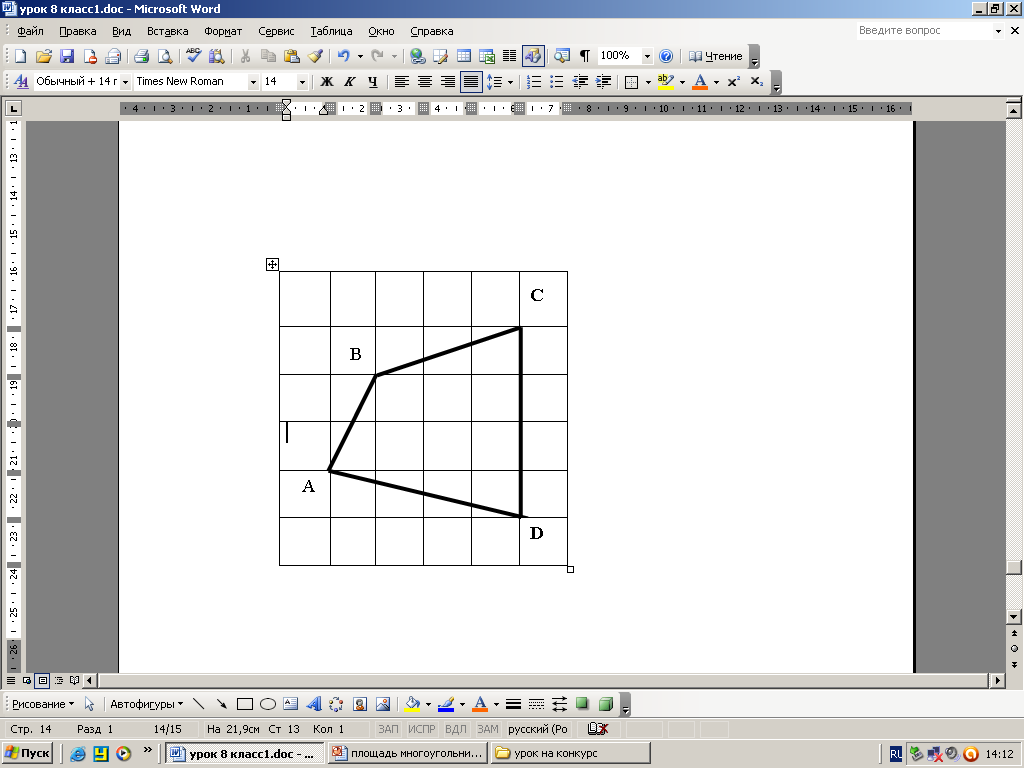 5.3.3. Ознакомление учащихся с «методом узелков», который применяется для вычисления площадей любых многоугольников. (слайд №12) Сейчас я хочу познакомить вас с методом «узелков», который применяется для вычисления площадей любых фигур. Используя этот метод, даже не зная формулу для вычисления площади, можно решить задачу. Например: сосчитаем количество «узелков» внутри фигуры (21) и количество «узелков» по контуру фигуры (16). Далее считаем по формуле: где m- количество «узелков» внутри фигуры, n- по периметру. Значит, площадь данного параллелограмма равна
6. Контроль усвоения полученных знаний по теме «Площадь многоугольников». Тест. | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
