Пояснительная записка Преподавание предмета «Математика»
 Скачать 282.52 Kb. Скачать 282.52 Kb.
|
  Пояснительная записка Пояснительная запискаПреподавание предмета «Математика» в 2014-2015 учебном году осуществляется в соответствии с нормативными и инструктивно-методическими документами Министерства образования и науки Российской Федерации, Министерства образования и науки Челябинской области:
2015 годы» (Распоряжение Правительства РФ от 07.02.2011 №163-р) Рабочая программа реализуется на основе Программы общеобразовательных учреждений (автор Бурмистрова Т.А ) и в учебниках математики и учебно-методических пособиях, созданных коллективом авторов под руководством Г.В. Дорофеева, С.Б.Суворовой, И.Ф.Шарыгина, по геометрии Л.С.Атанасяна. Общая характеристика учебного предмета Курс математики в классах общеобразовательного профиля дает представление о роли математики в современном мире, о способах применения математики в технике и в гуманитарных сферах. Математическое образование в основной школе складывается из следующих содержательных компонентов (точные названия блоков): арифметика; алгебра; геометрия; элементы комбинаторики, теории вероятностей, статистики и логики. В своей совокупности в них отражен богатый опыт обучения математике в нашей стране, учитывают современные тенденции отечественной и зарубежной школы и позволяют реализовать поставленные перед школьным образованием цели на информационно емком и практически значимом материале. Эти содержательные компоненты, развиваясь на протяжении всех лет обучения, естественным образом переплетаются и взаимодействуют в учебных курсах. Арифметика призвана способствовать приобретению практических навыков, необходимых для повседневной жизни. Она служит базой для всего дальнейшего изучения математики, способствует логическому развитию и формированию умения пользоваться алгоритмами. Алгебра нацелена на формирование математического аппарата для решения задач математики, смежных предметов, окружающей реальности. Язык алгебры подчеркивает значение математики как языка для построения математических моделей, процессов и явлений реального мира. Одной из основных задач изучения алгебры является развитие алгоритмического мышления, необходимого, в частности, для освоения курса информатики; овладение навыками дедуктивных рассуждений. Преобразование символических форм вносит свой специфический вклад в развитие воображения, способностей к математическому творчеству. Другой важной задачей изучения алгебры является получение школьниками конкретных знаний о функциях как важнейшей математической модели для описания и исследования разнообразных процессов (равномерных, равноускоренных, экспоненциальных, периодических и др.), для формирования у учащихся представлений о роли математики в развитии цивилизации и культуры. Геометрия– один из важнейших компонентов математического образования, необходимый для приобретения конкретных знаний о пространстве и практически значимых умений, формирования языка описания объектов окружающего мира, для развития пространственного воображения и интуиции, математической культуры, для эстетического воспитания учащихся. Изучение геометрии вносит вклад в развитие логического мышления, в формирование понятия доказательства. Элементы логики, комбинаторики, статистики и теории вероятностей становятся обязательным компонентом школьного образования, усиливающим его прикладное и практическое значение. Этот материал необходим, прежде всего, для формирования функциональной грамотности – умений воспринимать и анализировать информацию, представленную в различных формах, понимать вероятностный характер многих реальных зависимостей, производить простейшие вероятностные расчеты. Изучение основ комбинаторики позволит учащемуся осуществлять рассмотрение случаев, перебор и подсчет числа вариантов, в том числе в простейших прикладных задачах. При изучении статистики и теории вероятностей обогащаются представления о современной картине мира и методах его исследования, формируется понимание роли статистики как источника социально значимой информации, и закладываются основы вероятностного мышления. Таким образом, в ходе освоения содержания курса учащиеся получают возможность:
сформировать практические навыки выполнения устных, письменных, инструментальных вычислений, развить вычислительную культуру;
алгебраические умения и научиться применять их к решению математических и нематематических задач;
функционально-графические представления для описания и анализа реальных зависимостей;
основные факты и методы планиметрии, познакомиться с простейшими пространственными телами и их свойствами;
о различных способах их изучения, об особенностях выводов и прогнозов, носящих вероятностный характер;
суждения, проводить несложные систематизации, приводить примеры и контр примеры, использовать различные языки математики (словесный, символический, графический) для иллюстрации, интерпретации, аргументации и доказательства;
средствах математического моделирования реальных процессов и явлений. МЕСТО ПРЕДМЕТА В областном базисном учебном плане в 2014-15 учебном году общеобразовательной организации предлагается следующее примерное количество часов на преподавание учебного предмета «Математика» – 875 часов. Причем на изучение интегрированного предмета «Математика»
При изучении курса используются дидактические материалы уровневого характера (контрольные работы, тесты, самостоятельные работы, практические работы), которые обеспечивают дифференцированный уровень подготовки выпускников к успешному освоению стандарта математического образования и сдачи ГИА по математике. Особое внимание уделено отработке учащимися тем на итоговом повторении: основные методы решения квадратных, исследование свойств функций. В 2014-2015 учебном году данная рабочая программа реализуется в 7-9 классах, так как составлена на основе федерального компонента государственного стандарта математического образования. Программа рассчитана на 3 года. Цели и задачи изучения курса математики 7 - 9 классе Изучение математики на базовом и профильном уровнях среднего (полного) общего образования направлено на достижение следующих целей: формирование представлений о математике как универсальном языке науки, средстве моделирования явлений и процессов, об идеях и методах математики; развитие логического мышления, пространственного воображения, алгоритмической культуры, критичности мышления на уровне, необходимом для будущей профессиональной деятельности, а также последующего обучения в высшей школе ; овладение математическими знаниями и умениями, необходимыми в повседневной жизни, для изучения школьных естественнонаучных дисциплин на базовом уровне, для получения образования в областях, не требующих углубленной математической подготовки (базовый уровень); овладение устным и письменным математическим языком, математическими знаниями и умениями, необходимыми для изучения школьных естественно- научных дисциплин, для продолжения образования; воспитание средствами математики культуры личности, понимания значимости математики для научно-технического прогресса, отношения к математике как к части общечеловеческой культуры через знакомство с историей развития математики, эволюцией математических идей, понимание значимости математики для общественного прогресса. Содержание учебного предмета МАТЕМАТИКА. АЛГЕБРА. ГЕОМЕТРИЯ. Натуральные числа. Натуральный ряд. Десятичная система счисления. Арифметические действия с натуральными числами. Свойства арифметических действий. Степень с натуральным показателем. Числовые выражения, значение числового выражения. Порядок действий в числовых выражениях, использование скобок. Решение текстовых задач арифметическими способами. Делители и кратные. Свойства и признаки делимости. Простые и составные числа. Разложение натурального числа на простые множители. Деление с остатком. Дроби. Обыкновенные дроби. Основное свойство дроби. Сравнение обыкновенных дробей. Арифметические действия с обыкновенными дробями. Нахождение части от целого и целого по его части. Десятичные дроби. Сравнение десятичных дробей. Арифметические действия с десятичными дробями. Представление десятичной дроби в виде обыкновенной дроби и обыкновенной в виде десятичной. Проценты; нахождение процентов от величины и величины по её процентам. Отношение; выражение отношения в процентах. Пропорция; основное свойство пропорции. Решение текстовых задач арифметическими способами. Рациональные числа. Положительные и отрицательные числа, модуль числа. Множество целых чисел. Множество рациональных чисел; рациональное число как отношение m/n, где т — целое число, а n — натуральное. Сравнение рациональных чисел. Арифметические действия с рациональными числами. Свойства арифметических действий. Степень с целым показателем. Действительные числа. Квадратный корень из числа. Корень третьей степени. Понятие об иррациональном числе. Иррациональность числа и несоизмеримость стороны и диагонали квадрата. Десятичные приближения иррациональных чисел. Множество действительных чисел; представление действительных чисел бесконечными десятичными дробями. Сравнение действительных чисел. Координатная прямая. Изображение чисел точками координатной прямой. Числовые промежутки. Измерения, приближения, оценки. Размеры объектов окружающего мира (от элементарных частиц до Вселенной), длительность процессов в окружающем мире. Выделение множителя — степени десяти в записи числа. Приближённое значение величины, точность приближения. Округление натуральных чисел и десятичных дробей. Прикидка и оценка результатов вычислений. Алгебраические выражения. Буквенные выражения (выражения с переменными). Числовое значение буквенного выражения. Допустимые значения переменных. Подстановка выражений вместо переменных. Преобразование буквенных выражений на основе свойств арифметических действий. Равенство буквенных выражений. Тождество. Степень с натуральным показателем и её свойства. Одночлены и многочлены. Степень многочлена. Сложение, вычитание, умножение многочленов. Формулы сокращённого умножения: квадрат суммы и квадрат разности. Формула разности квадратов. Преобразование целого выражения в многочлен. Разложение многочленов на множители. Многочлены с одной переменной. Корень многочлена. Квадратный трёхчлен; разложение квадратного трёхчлена на множители. Алгебраическая дробь. Основное свойство алгебраической дроби. Сложение, вычитание, умножение, деление алгебраических дробей. Степень с целым показателем и её свойства. Рациональные выражения и их преобразования. Доказательство тождеств. Квадратные корни. Свойства арифметических квадратных корней и их применение к преобразованию числовых выражений и вычислениям. Уравнения. Уравнение с одной переменной. Корень уравнения. Свойства числовых равенств. Равносильность уравнений. Линейное уравнение. Квадратное уравнение: формула корней квадратного уравнения. Теорема Виета. Решение уравнений, сводящихся к линейным и квадратным. Примеры решения уравнений третьей и четвёртой степеней. Решение дробно-рациональных уравнений. Уравнение с двумя переменными. Линейное уравнение с двумя переменными, примеры решения уравнений в целых числах. Система уравнений с двумя переменными. Равносильность систем. Системы двух линейных уравнений с двумя переменными; решение подстановкой и сложением. Примеры решения систем нелинейных уравнений с двумя переменными. Решение текстовых задач алгебраическим способом. Декартовы координаты на плоскости. Графическая интерпретация уравнения с двумя переменными. График линейного уравнения с двумя переменными; угловой коэффициент прямой; условие параллельности прямых. Графики простейших нелинейных уравнений: парабола, гипербола, окружность. Графическая интерпретация систем уравнений с двумя переменными. Неравенства. Числовые неравенства и их свойства.Неравенство с одной переменной. Равносильность неравенств. Линейные неравенства с одной переменной. Квадратные неравенства. Системы неравенств с одной переменной. Функции. Примеры зависимостей; прямая пропорциональность, обрат-ная пропорциональность. Задание зависимостей формулами; вычисления по формулам. Зависимости между величинами. Примеры графиков зависимостей, отражающих реальные процессы. Числовые функции. Понятие функции, область применения и область значения функции. Способы задания функции. График функции. Свойства функции, их отражение на графике. Функции, описывающие прямую и обратную пропорциональные зависимости, их графики и свойства. Линейная функция, её график и свойства. Квадратичная функция, её график и свойства. Степенные функции с натуральными показателями 2 и 3, их графики и свойства. Графики функций Числовые последовательности. Понятие числовой последовательности. Задание последовательности рекуррентной формулой и формулой n-го члена. Арифметическая и геометрическая прогрессии. Формулы n-го члена арифметической и геометрической прогрессий, суммы первых п-х членов. Изображение членов арифметической и геометрической прогрессий точками координатной плоскости. Линейный и экспоненциальный рост. Сложные проценты. Статистические данные. Представление данных в виде таблиц, диаграмм, графиков. Случайная изменчивость. Статистические характеристики набора данных: среднее арифметическое, медиана, наибольшее и наименьшее значения, размах. Представление о выборочном исследовании. Случайные события и вероятность. Понятие о случайном опыте и случайном событии. Частота случайного события. Статистический подход к понятию вероятности. Вероятности противоположных событий. Достоверные и невозможные события. Равновозможность событий. Классическое определение вероятности. Комбинаторика. Решение комбинаторных задач перебором вариантов. Комбинаторное правило умножения. Перестановки и факториал. Наглядная геометрия. Наглядные представления о фигурах на плоскости: прямая, отрезок, луч, угол, ломаная, многоугольник, окружность, круг. Четырёхугольник, прямоугольник, квадрат. Треугольник, виды треугольников. Правильные многоугольники. Взаимное расположение двух прямых, двух окружностей, прямой и окружности. Изображение геометрических фигур и их конфигураций. Длина отрезка, ломаной. Периметр многоугольника. Единицы измерения длины. Измерение длины отрезка, построение отрезка заданной длины. Виды углов. Градусная мера угла. Измерение и построение углов с помощью транспортира. Биссектриса угла. Понятие площади фигуры; единицы измерения площади. Площадь прямоугольника, квадрата. Приближённое измерение площади фигур на клетчатой бумаге. Равновеликие фигуры. Разрезание и составление геометрических фигур. Наглядные представления о пространственных фигурах: куб, параллелепипед, призма, пирамида, шар, сфера, конус, цилиндр. Изображение пространственных фигур. Примеры сечений. Многогранники. Правильные многогранники. Примеры развёрток многогранников, цилиндра и конуса. Изготовление моделей пространственных фигур. Понятие объёма; единицы объёма. Объём прямоугольного параллелепипеда, куба. Понятие о равенстве фигур. Центральная, осевая и зеркальная симметрии. Изображение симметричных фигур. Геометрические фигуры. Прямые и углы. Точка, прямая, плоскость. Отрезок, луч. Угол. Виды углов. Вертикальные и смежные углы. Биссектриса угла. Параллельные и пересекающиеся прямые. Перпендикулярные прямые. Теоремы о параллельности и перпендикулярности прямых. Перпендикуляр и наклонная к прямой. Серединный перпендикуляр к отрезку. Геометрическое место точек. Свойства биссектрисы угла и серединного перпендикуляра к отрезку. Треугольник. Высота, медиана, биссектриса, средняя линия треугольника. Равнобедренные и равносторонние треугольники; свойства и признаки равнобедренного треугольника. Признаки равенства треугольников. Неравенство треугольника. Соотношения между сторонами и углами треугольника. Сумма углов треугольника. Внешние углы треугольника. Теорема Фалеса. Подобие треугольников. Признаки подобия треугольников. Теорема Пифагора. Синус, косинус, тангенс, котангенс острого угла прямоугольного треугольника и углов от 0 до 180°, приведение к острому углу. Решение прямоугольных треугольников. Основное тригонометрическое тождество. Формулы, связывающие синус, косинус, тангенс, котангенс одного и того же угла. Решение треугольников: теорема косинусов и теорема синусов. Замечательные точки треугольника. Четырёхугольник. Параллелограмм, его свойства и признаки. Прямоугольник, квадрат, ромб, их свойства и признаки. Трапеция, средняя линия трапеции. Многоугольник. Выпуклые многоугольники. Сумма углов выпуклого многоугольника. Правильные многоугольники. Окружность и круг. Дуга, хорда. Сектор, сегмент. Центральный угол, вписанный угол; величина вписанного угла. Взаимное расположение прямой и окружности, двух окружностей. Касательная и секущая к окружности, их свойства. Вписанные и описанные многоугольники. Окружность, вписанная в треугольник, и окружность, описанная около треугольника. Вписанные и описанные окружности правильного многоугольника. Геометрические преобразования. Понятие о равенстве фигур. Понятие о движении: осевая и центральная симметрии, параллельный перенос, поворот. Понятие о подобии фигур и гомотетии. Решение задач на вычисление, доказательство и построение с использованием свойств изученных фигур. Измерение геометрических величин. Длина отрезка. Расстояние от точки до прямой. Расстояние между параллельными прямыми. Периметр многоугольника. Длина окружности, число п, длина дуги окружности. Градусная мера угла, соответствие между величиной центрального угла и длиной дуги окружности. Понятие площади плоских фигур. Равносоставленные и равновеликие фигуры. Площадь прямоугольника. Площади параллелограмма, треугольника и трапеции. Площадь многоугольника. Площадь круга и площадь сектора. Соотношение между площадями подобных фигур. Решение задач на вычисление и доказательство с использованием изученных формул. Координаты. Уравнение прямой. Координаты середины отрезка. Формула расстояния между двумя точками плоскости. Уравнение окружности. Векторы. Длина (модуль) вектора. Равенство векторов. Коллинеарные векторы. Координаты вектора. Умножение вектора на число, сумма векторов, разложение вектора по двум неколлинеарным векторам. Скалярное произведение векторов. 9 класс Алгебра 1. Неравенства (19ч,в том числе контрольная работа-1 час) Действительные числа как бесконечные десятичные дроби. Числовые неравенства и их свойства. Доказательство числовых и алгебраических неравенств. Линейные неравенства с одной пере менной и их системы. Точность приближения, относительная точность. 2. Квадратичная функция(20 ч, в том числе контрольная работа-1 час) Функция у = ax2 + bх + с и ее график. Свойства квадратичной функции: возрастание и убывание, сохранение знака на проме жутке, наибольшее (наименьшее) значение. Решение неравенств второй степени с одной переменной. 3. Уравнения и системы уравнений (25ч, в том числе контрольные работы-2 час) Рациональные выражения. Допустимые значения переменных, входящих в алгебраические выражения. Тождество, доказательство тождеств. Решение целых и дробных уравнений с одной переменной. Примеры решения нелинейных систем уравнений двумя переменными. Решение текстовых задач. Графическая интерпретация решения уравнений и систем уравнений. 4. Арифметическая и геометрическая прогрессии (17ч, в том числе контрольная работа-1 час) Арифметическая и геометрическая прогрессии. Формулы п-го члена и суммы п членов арифметической и геометрической прогрессий. Простые и сложные проценты. 5.Статистические исследования (6ч) Генеральная совокупность и выборка. Ранжирование данных. Полигон частот. Интервальный ряд. Гистограмма. Выборочная дисперсия, среднее квадратичное отклонение. 6. Повторение (15ч) Геометрия 1.Векторы. (8 ч.) Понятие вектора. Равенство векторов. Сложение и вычитание векторов. Умножение вектора на число. Применение векторов при решении задач. 2. Метод координат. (10 ч, в том числе контрольная работа – 1ч) Координаты вектора. Простейшие задачи в координатах. Уравнения окружности и прямой. Применение векторов и координат при решении задач. 3.Соотношения между сторонами и углами треугольника. Скалярное произведение векторов. (11ч, в том числе контрольная работа -1ч) Синус, косинус, тангенс угла. Теоремы синусов и косинусов. Решение треугольников. Скалярное произведение векторов и его применение в геометрических задачах. 4. Длина окружности и площадь круга (12ч, в том числе контрольная работа-1ч) Правильные многоугольники. Окружности, описанная около правильного многоугольника и вписанная в него. Построение правильных многоугольников. Длина окружности. Площадь круга. 5. Движения (8ч, в том числе контрольная работа – 1ч) Отображение плоскости на себя. Понятие движения. Осевая и центральная симметрии. Параллельный перенос. Поворот. Наложения и движения. 6. Начальные сведения из стереометрии (8ч.) Предмет стереометрии. Геометрические тела и поверхности. Многогранники: призма, параллелепипед, пирамида, формулы для вычисления их объемов. Тела и поверхности вращения: цилиндр, сфера, шар, конус, формулы для вычисления их площадей и объемов 7. Об аксиомах планиметрии (2ч ) 8. Итоговое повторение. (9ч ) 8 класс Алгебра 1. Алгебраические дроби (23 ч, в том числе контрольная работа -1час ) Алгебраическая дробь. Основное свойство алгебраической дро би. Сокращение дробей. Сложение, вычитание, умножение и деление алгебраических дробей. Степень с целым показателем и ее свойства. Выделение множителя — степени десяти — в записи числа. 2. Квадратные корни (17ч, в том числе контрольная работа-1ч) Квадратный корень из числа. Понятие об иррациональном числе. Десятичные приближения квадратного корня. Свойства арифметического квадратного корня и их применение к пре образованию выражений. Корень третьей степени, понятие о корне n-ой-степени из числа. Нахождение приближенного значения корня с помощью калькулятора. Графики зависимостей 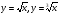 . .3. Квадратные уравнения (20ч, в том числе контрольная работа-1ч) Квадратное уравнение. Формулы корней квадратного уравнения. |Решение текстовых задач составлением квадратных уравнений. Теорема Виета. Разложение на множители квадратного трехчлена. 4. Системы уравнений (18ч, в том числе контрольная работа-1ч) Уравнение с двумя переменными. Линейное уравнение с дву мя переменными и его график. Примеры решения уравнений в целых числах. Система уравнений; решение систем двух линей ных уравнений с двумя переменными, графическая интерпрета ция. Примеры решения нелинейных систем. Решение текстовых задач составлением систем уравнений. Уравнение с несколькими переменными. 5. Функции (14ч, в том числе контрольная работа-1ч) Функция. Область определения и область значений функции. График функции. Возрастание и убывание функции, сохранение знака на промежутке, нули функции. Функции у = kx, у = kx + l, 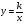 — и их графики. Примеры графических зависимостей, отражающих реальные процессы. — и их графики. Примеры графических зависимостей, отражающих реальные процессы.6. Вероятность и статистика (6ч, в том числе контрольная работа-1ч) Статистические характеристики ряда данных, медиана, сред нее арифметическое, размах. Таблица частот. Вероятность равновозможных событий. Классическая формула вычисления ве роятности события и условия ее применения. Представление о геометрической вероятности. 7. Повторение (7ч) Геометрия 1. Четырехугольники (14 ч, в том числе контрольная работа-1ч) Многоугольник, Выпуклый многоугольник, четырехугольник. Параллелограмм, его свойства и признаки. Трапеция. Прямоугольник, ромб, квадрат, их свойства. Осевая и центральная симметрии. 2. Площадь (14ч, в том числе контрольная работа – 1ч) Понятие площади. Площадь прямоугольника, параллелограмма, треугольника, трапеции. Теорема Пифагора. 3. Подобные треугольники (19ч, в том числе контрольные работы – 2ч) Подобные треугольники. Признаки подобия треугольников. Применение подобия к доказательству теорем и решению задач. Синус, косинус, тангенс острого угла прямоугольного треугольника. 4. Окружность (17ч, в том числе контрольная работа – 1ч) Взаимное расположение прямой и окружности. Касательная к окружности, ее свойство признак. Центральные и вписанные углы. Четыре замечательные точки треугольника. Вписанная и описанная окружности. 5. Повторение (6ч) 7 класс Алгебра 1. Дроби и проценты (16 часов, из них контрольная работа-1час) Обыкновенные и десятичные дроби, представление обыкновенных дробей десятичными. Сравнение рациональных чисел. Понятие степени с натуральным показателем. Решение задач на проценты. Статистические характеристики: среднее арифметическое, мода и размах. 2. Прямая и обратная пропорциональности (10 часов, контрольная работа- 1 час) Отношение, выражение отношения в процентах. Определение пропорции. Основное свойство пропорции. Прямо пропорциональная и обратно пропорциональная зависимости, формулы этих зависимостей. 3. Введение в алгебру (11 часов, из них контрольная работа-1 час) Буквенные выражения. Числовое значение буквенного выражения. Преобразование буквенных выражений: раскрытие скобок, приведение подобных слагаемых. 4. Уравнения (15 часов, из них контрольная работа-1 час) Уравнение. Корни уравнения. Линейное уравнение. Решение текстовых задач методом составления линейных уравнений. 5. Координаты и графики (12 часов, из них контрольная работа-1час) Числовые промежутки: интервал, отрезок, луч. Формула расстояния между точками координатной прямой. Множества точек на координатной плоскости. Графики зависимостей y=x, y=-x, y=x2, y=x3, y=׀x׀. Графики реальных зависимостей. 6. Свойства степени с натуральным показателем (10 часов, из них контрольная работа1 час) Произведение и частное степеней с натуральным показателем. Степень степени, произведения и дроби. Формула перестановок. 7. Многочлены (18 часов, из них контрольные работы -2часа) Одночлены и многочлены. Сложение, вычитание и умножение многочленов. Формулы квадрата суммы и разности, куб суммы и куб разности. Решение задач с помощью линейных уравнений. 8. Разложение многочленов на множители (20 часов, из них контрольная работа-1 час) Разложение многочлена на множители. Вынесение общего множителя за скобки. Способ группировки. Формула разности квадратов. Формулы разности и суммы кубов. Решение уравнений с помощью разложения на множители. 9. Частота вероятность (5 часа, из них контрольная работа-1 час) Частота случайного события. Оценка вероятности случайного события по частоте. Повторение (6часов) Геометрия 1.Начальные геометрические сведения (7часов, в том числе 1ч- контрольная работа) Начальные понятия планиметрии. Геометрические фигу ры. Понятие о равенстве фигур. Отрезок. Равенство отрезков. Длина отрезка и ее свойства. Угол. Равенство углов. Величина угла и ее свойства. Смежные и вертикальные углы и их свой ства. Перпендикулярные прямые. 2.Треугольники (14часов, в том числе 1ч- контрольная работа) Треугольник. Признаки равенства треугольников. Перпен дикуляр к прямой. Медианы, биссектрисы и высоты треуголь ника. Равнобедренный треугольник и его свойства. Основные задачи на построение с помощью циркуля и линейки. 3.Параллельные прямые (9часов, в том числе 1ч- контрольная работа) Признаки параллельности прямых. Аксиома параллельных прямых. Свойства параллельных прямых. 4.Соотношения между сторонами и углами треугольника (16часов, в том числе 1ч- контрольная работа) Сумма углов треугольника. Соотношения между сторонами и углами треугольника. Неравенство треугольника. Некоторые свойства прямоугольных треугольников. Признаки равенства прямоугольных треугольников. Расстояние от точки до прямой. Расстояние между параллельными прямыми. Задачи на пост роение. 5.Повторение. Решение задач.(6часов) ТРЕБОВАНИЯ К УРОВНЮ ПОДГОТОВКИ ВЫПУСКНИКОВ В результате изучения математики ученик должен знать/понимать
Алгебра уметь
использовать приобретенные знания и умения в практической деятельности и повседневной жизни для:
Элементы логики, комбинаторики, статистики и теории вероятностей уметь
использовать приобретенные знания и умения в практической деятельности и повседневной жизни для:
В ходе преподавания алгебры в 7-9 классах, работы над формированием у учащихся перечисленных в программе знаний и умений, следует обращать внимание на то, чтобы они овладевали умениями общеучебного характера, разнообразными способами деятельности, приобретали опыт:
Геометрия Уметь
распознавать геометрические фигуры, различать их взаимное расположение;
использовать приобретенные знания и умения в практической деятельности в повседневной жизни для
|