1. y = x 2; y = x + 2; y = x
 Скачать 15.09 Kb. Скачать 15.09 Kb.
|
 1. Из предложенных формул выберите ту формулу, которая задает функцию, представленную на графике 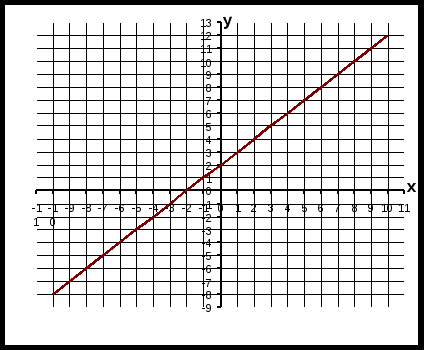 1). y = x – 2; 2). y = x + 2; 3). y = x2; 4). y = 4/x. 2. Из предложенных формул выберите ту формулу, которая задает функцию, представленную на графике 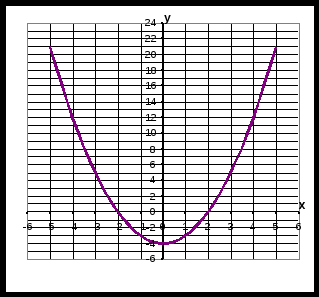 1). y = x – 2; 2). y = x2 + 2; 3). y = x2-2; 4). y = 4/x. 3. Из предложенных формул выберите ту формулу, которая задает функцию, представленную на графике 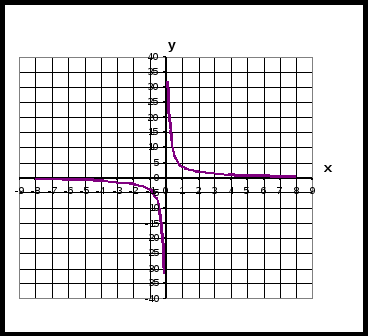 1). y = x – 2; 2). y = x2 + 2; 3). y = x2-2; 4). y = 4/x. 4. . Лыжник вышел из поселка и через t ч оказался на расстоянии S км от него. Запишите формулу, задающую зависимость S от t, если скорость лыжника была равна 10 км/ч. а) S=10t; б) S=10+t; в) S=10-t. 5. Зависимость калорийности молока от его жирности можно выразить формулой k=100a+330, где k – калорийность молока в калориях, а – процент жира в молоке. Является ли эта зависимость линейной функцией? Исходя из личного опыта, укажите, какие из предложенных множеств наиболее точно задают область определения А и область значений K функции. а) А – все положительные числа, K – все положительные числа. б) А – все числа, удовлетворяющие неравенству 0<а<10, K – все положительные числа, удовлетворяющие неравенству 330<а<1330. в) А – натуральные числа от 0 до 10, K- натуральные числа от 330 до 1330. 6. Используя формулу S=x2, где S – площадь квадрата, х – длина его стороны, определите, как изменится площадь квадрата, если его сторону увеличить в 10 раз? а) увеличится в 10 раз; б) увеличится в 20 раз; в) увеличится в 100 раз. 7. Комета удаляется от Земли по параболе, задаваемой уравнением S=100000+ t·v², где v – скорость кометы, S – расстояние от кометы до Земли, t – время. Какое расстояние будет между кометой и Землей через один месяц, если v = 10 км/с? а) 259300000 км, б) 72000000км, в) 7300000 км. 8. Для y=x3 найдите значение аргумента, соответствующее значению функции, равному 125. а) x=25; б) x=5 в) x=1. |