Учебнику «Алгебра и начала анализа» авторы: Ю. М. Колягин, Ю. В. Сидоров, М. В. Ткачева, Н. Е. Федорова, М. И. Шабунин. Тема: Первообразная. Цель урока: Ввести понятие первообразной для функции
 Скачать 47.18 Kb. Скачать 47.18 Kb.
|
| Разработка урока по алгебре и началам анализа в 11 классе (для учителей, работающих по учебнику « Алгебра и начала анализа» авторы: Ю.М. Колягин, Ю.В. Сидоров, М.В. Ткачева, Н.Е. Федорова, М.И. Шабунин). Тема: Первообразная. Цель урока:
Тип урока: Комбинированный. Оборудование: Таблицы, проектор. Обязательные результаты обучения на данном уроке:
Ход урока:
Вывод: Все известные нам действия парные, то есть имеют обратные, поэтому естественно поискать обратное действие и для дифференцирования.
И так возникла проблема: есть ли обратное действие дифференцированию, и какие задачи к нему приводят? Для этого надо вспомнить все о прямом действие – действии нахождения производной функции. Учащиеся отвечают на вопросы.
Ответ: ��=  ; ��'= ; ��'=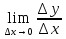 - скорость изменения функции. - скорость изменения функции.
Ответ: мгновенная скорость.
Ответ: тангенс угла наклона касательной к положительному направлению оси ОХ (на экране проецируется чертеж). А теперь сформируем обратные задачи:
Вывод: Существуют действие, обратное нахождению производной, следовательно, как любое действие оно должно иметь название и символ. Действие, обратное дифференцированию это действие нахождения первообразной и называется – интегрирование. Определение первообразной: Функция �� 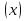 называется первообразной для функции называется первообразной для функции  на некотором промежутке, если для всех �� из этого промежутка �� на некотором промежутке, если для всех �� из этого промежутка ��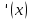 = = . .Пример: 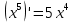 ��  - первообразная для функции - первообразная для функции 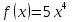 . .Функция  - первообразная для функции - первообразная для функции  , так как , так как  . .
Повторяются все правила и формулы нахождения производной.
 Вопрос: сколько первообразных можно найти в этой задаче? Все упражнения на нахождение первообразной сопровождаются проверкой по определенной производной. После решения таких задач делается предположение: в первообразной степенной функции показатель увеличивается на единицу, а в знаменателе появляется множитель, равны показателю: 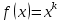 �� ��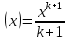 Проверяется гипотеза доказательством: ��'  Далее обращается внимание учащихся на тот факт, что первообразная не изменится, если к функции прибавить постоянную величину С, то есть ��  является первообразной для функции является первообразной для функции  , а также функция �� , а также функция ��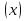 является первообразной функции является первообразной функции  на таком промежутке, на котором обе функции �� на таком промежутке, на котором обе функции ��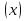 и и  определены. определены.
Понятия функции, предела, производной и интеграла является основными понятиями математического анализа. Далее краткая историческая справка. Термин «Функция» впервые был употреблен в 1692 году немецким математиком Г. Лейбницем, над этим понятием работали швейцарский математик И. Бернулли, Л. Эйлер, П. Дирихле, а также великий русский математик Н. И. Лобачевский. Первое определение предела дал английский математик Д. Валлис в 1616 году, И Ньютону принадлежит введение символа ������. Большой вклад в развитие дифференциального исчисления внесли французские ученые П. Ферма и Р. Декарт. Труды Кеплера, Кавальери служили основой теории интегрального исчисления. Развитие этой теории продолжили Эйлер и в России – П. А. Чебышев.
|
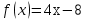 ;
; 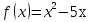 ;
; 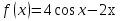
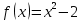
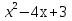 (показать на таблице) обратная задача: по построенному графику составить уравнение функции.
(показать на таблице) обратная задача: по построенному графику составить уравнение функции. , обратная задача: по найденным корням ��1=2; ��2=7 составить исходное уравнение. Для решения этих обратных задач мы использовали уравнение прямой ��=����+��, в котором по графику находили �� и ��; уравнение параболы, в котором по графику находили координаты вершины направление ветвей, точки пересечения с осями и т.д. Для решения задачи мы использовали свойства корней квадратного уравнения. А теперь сформируем две следующие задачи:
, обратная задача: по найденным корням ��1=2; ��2=7 составить исходное уравнение. Для решения этих обратных задач мы использовали уравнение прямой ��=����+��, в котором по графику находили �� и ��; уравнение параболы, в котором по графику находили координаты вершины направление ветвей, точки пересечения с осями и т.д. Для решения задачи мы использовали свойства корней квадратного уравнения. А теперь сформируем две следующие задачи: +4
+4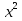 ;
; =
=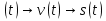
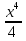 ,
,  .
. ,
, 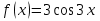 .
.