Учебникам «Алгебра 8» [aвторы: Ю. Н. Макарычев и др.] и «Геометрия 8»
 Скачать 79.92 Kb. Скачать 79.92 Kb.
|
| Спецификация работы для промежуточной аттестации по математике в 8 классе. Данный материал является спецификацией итоговой работы учащихся, обучающихся по учебникам «Алгебра 8» [aвторы: Ю. Н. Макарычев и др.] и «Геометрия 8» [aвторы: Л.С. Атанасян и др.] для общеобразовательных учреждений Назначение итоговой работы – оценить уровень овладения учащимися программным материалом, учесть полученные результаты при составлении рабочей программы, дифференцируя уровень заданий по содержательным линиям. Работа направлена на проверку достижение уровня обязательной подготовки. Работа состоит из двух частей. Первая часть содержит 20 заданий, соответствующих минимуму содержания курса «Алгебра 8» и «Геометрия 8». 10 заданий – «Алгебра», 5 заданий – «Геометрия» и 5 заданий – «Реальная математика». С помощью этих заданий проверяется умение владеть основными понятиями, знание алгоритмов при выполнении определённых процедур, а также применение изученного материала в простейших практических ситуациях. Предусмотрены две формы ответа: задания с выбором ответа из четырёх предложенных; задания с кратким ответом. Вторая часть содержит 6 заданий: 3 задания - «Алгебра» и 3 задания - «Геометрия». На выполнение работы отводится 80 минут (два урока). Задания части 1 выполняются непосредственно в бланке с текстами заданий. В заданиях с выбором ответа ученик отмечает тот ответ, который считает верным; в заданиях с кратким ответом – вписывает ответ в отведённое место. Задания части 2 выполняются на отдельном листе с полным решением. Каждое верно выполненное задание части 1 оценивается в 1 балл, а каждое верно выполненное задание части 2 оценивается в 2 балла. Задание считается выполненным, если верно обведён номер ответа, или верно записан ответ, верно приведено решение. Для оценивания результатов выполнения работ применяются отметки «2», «3», «4», «5» и рейтинг от 0 до 32 баллов. Каждое верно выполненное задание оценивается в 1 балл.
1 вариант. 1 часть. Алгебра. А1. Сравните 4√3 и √48.
А2. Вычислите √ 0,09 * 81 Ответ: ___________ А3. Решите уравнение: х2 - 9 = 0
А4. Решите неравенство: 5х + 8 ≤ 4х – 12 Ответ: ___________ А5. На каком чертеже изображён график функции у = - 3/х. 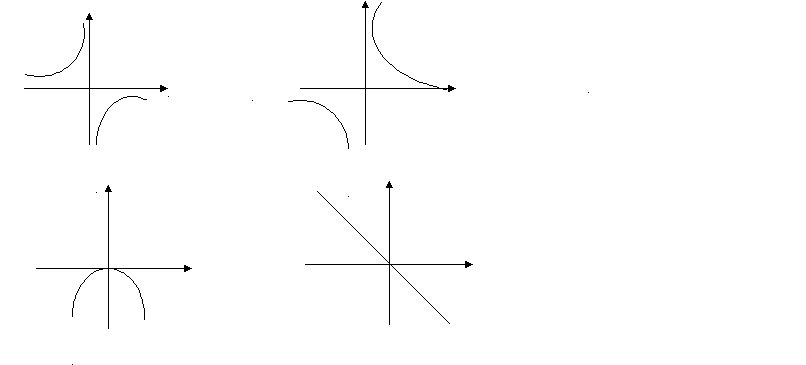 А6. Для каждого выражения из первой строки укажите тождественно равное ему выражение из нижней строки А с4 * с-4 Б (с-4)4 В с-2 /с6 1. с0 2. с4 3. с-16 4. с-8 А7. Запишите в стандартном виде число 1302. 1.130,2 * 10 2.13,02 * 102 3. 0,1302 * 104 4. 1,302 * 103 А8. Решите уравнение 3х2 + х – 4 = 0 1. -8/3; 2 2. 1; -4/3 3. -1; 4/3 4. 4; -3 А9. Сократите дробь: (а2 – 9в2)/(3а – 9в) 1. (а + 3в)/3 2. (а – 3в)/3 3. (а – в)/3 4.(3в – а)/3 А10. Выполните вычитание дробей (11а – 4)/14а – (3а – 2)/14а 1. (4а - 3)/7а 2. (4а – 1)/7а 3. (8а – 6)/7а 4. (7а – 2)/7а Геометрия. А11. Катеты прямоугольного треугольника равны 6 см и 8 см. Найдите длину гипотенузы. Ответ: _____________________ А12. Один из углов параллелограмма на 500 меньше другого. Найдите все углы параллелограмма. Ответ: _____________________ А13. Подобны ли треугольники, изображённые на рисунке? Ответ: _____________________ 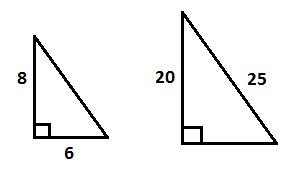 А14. Найдите высоту ромба, сторона которого равна 6,5 см, а площадь – 26 см2. Ответ: _____________________ А15. Расстояние от точки окружности до концов диаметра равны 9 см и 12 см. Найдите радиус окружности. Ответ: _____________________ Реальная математика. А16.В таблице приведены результаты забега участников соревнований. Зачёт выставлялся, если показан результат не хуже 9,5 с. Кто из участников получил зачёт?
А17. На диаграммах представлены результаты контрольной работа по алгебре в 8 классе четырёх школ. 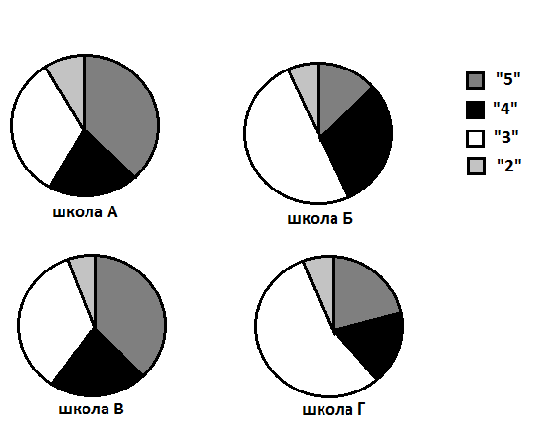 3 В какой школе процент учащихся, получивших четвёрки, больше 25% ? 1. А 2. Б 3. В 4. Г На приведённой ниже диаграмме показано изменение стоимости одной акции ОАО «Молоко» в течении 10 рабочих дней  Используя эту диаграмму, решите задачи: А18. Сколько дней курс акций бал выше 1500 рублей? 1. 1 2. 2 3. 6 4. 7 А19. В какой день был самый высокий курс акций? 1. 6 2. 8 3. 3 4. 10 Автомобильный концерн выпустил две новые модели автомобилей: модель А и модель Б. На графиках показано, как автомобили этих марок продавались в течении 2012 года. Используя график, ответьте на вопрос: 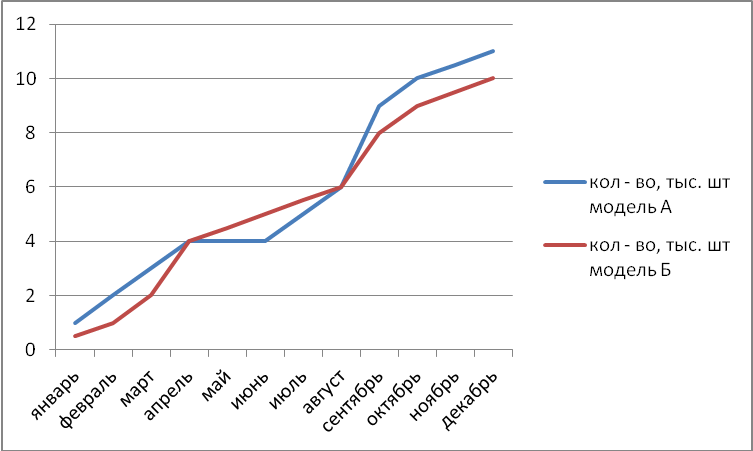 А20. Сколько автомобилей этих двух моделей было продано за последние 4 месяца года? Ответ: ______________________ 2 часть. Алгебра. В1. Один из катетов прямоугольного треугольника в 2 раза меньше другого. Найдите меньший кА тет, если гипотенуза равна 15. В2.Решите уравнение: (х2 + 4х)/(х – 3) – (4х + 9)/(х – 3) = 0 В3.Известно, что 1 ≤ х ≤ 3, 4 ≤ у ≤ 5. Оцените значение выражения х – 2у. Геометрия. В4. Периметр ромба равен 40 см, а один из его углов равен 600. Найдите длину диагонали, противолежащей этому углу. В5. Средняя линия трапеции равна 20 см. Найдите основания трапеции, если они относятся как 3:7. В6. Проекции катетов на гипотенузу прямоугольного треугольника равны 9 см и 16 см. Найдите катеты треугольника. 2 вариант. Алгебра. А1. Сравните 3√7 и √63. 1. 3√7 > √63 2. 3√7 < √63 3. 3√7 = √63 4. другой ответ А2. Вычислите √ 9 * 0,0004. Ответ: ___________ А3. Решите уравнение: х2 - 16 = 0
А4. Решите неравенство: 3х - 4 ≥ 2х + 7 Ответ: ___________ А5. На каком чертеже изображён график функции у = - 1/х. 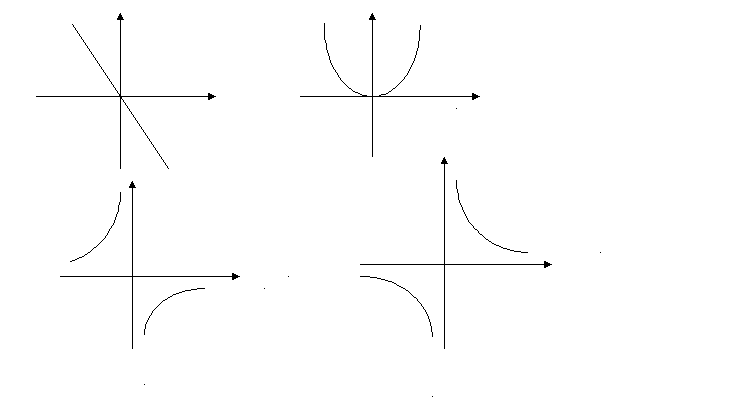 А6. Для каждого выражения из первой строки укажите тождественно равное ему выражение из нижней строки А а2 * а-10 Б (а-6)2 В а-6 /а -2 1. а-4 2. а-12 3. а-20 4. а-8 А7. Запишите в стандартном виде число 30400. 1. 30,4 * 10 2. 3,04 * 104 3. 304 * 102 4. 0,304 * 105 А8. Решите уравнение 2х2 + х - 3 = 0 1. 1; -3/2; 2. 3; -2 3. (1 + √ 7) /4; 4.(1 - √ 7) /4; А9. Сократите дробь: (х – 5)2/(2х – 10) 1. (х – 5)/2 2. (х + 5)/2 3. (5 – х)/2 4. (х – 5)/ 10 А10. Выполните вычитание дробей (m + n)/2mn – (m – n)/2mn 1. 1/m 2. 0 3. 1/n 4. 1/2mn Геометрия. А11. Гипотенуза прямоугольного треугольного треугольника равна 15 см, а один из его катетов – 12 см. Найдите длину второго катета. Ответ: _____________________ А12.Один из углов параллелограмма в 3 раза больше другого. Найдите все углы параллелограмма. Ответ: _____________________ А13. Подобны ли треугольники, изображённые на рисунке? Ответ: _____________________ 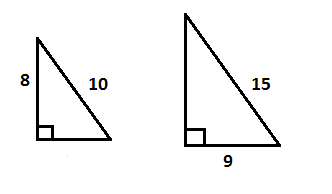 А14. Найдите сторону ромба, высота которого равна 2,4 см, а площадь – 12 см2. Ответ: _____________________ А15. Радиус окружности равен 10 см, а расстояние от одного конца диаметра до точки окружности – 16 см. Найдите расстояние от другого конца диаметра до этой точки. Ответ: _____________________ Реальная математика. А16.В таблице приведены результаты забега участников соревнований. Зачёт выставлялся, если показан результат не хуже 11,5 с. Кто из участников получил зачёт?
А17. На диаграммах представлены результаты контрольной работа по алгебре в 8 классе четырёх школ. 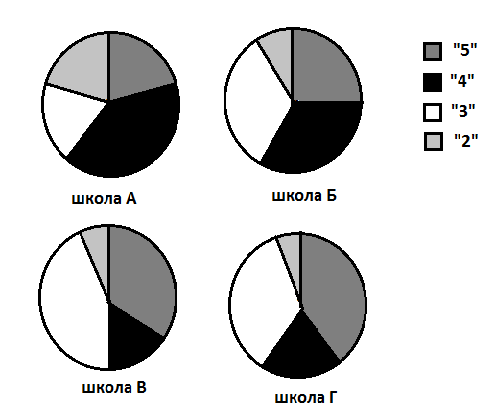 В какой школе процент учащихся, получивших тройки, меньше 25% ? 1. А 2. Б 3. В 4. Г На приведённой ниже диаграмме показано изменение стоимости одной акции ОАО «Хлеб» в течении 10 рабочих дней.  Используя эту диаграмму, решите задачи: А18. Сколько дней курс акций был ниже 1500 рублей? 1. 1 2. 5 3. 3 4. 4 А19. На сколько дороже продавались акции на 10й день, чем во второй? Ответ: __________________________ Автомобильный концерн выпустил две новые модели автомобилей: модель А и модель Б. На графиках показано, как автомобили этих марок продавались в течении 2012 года. Используя график, ответьте на вопрос: 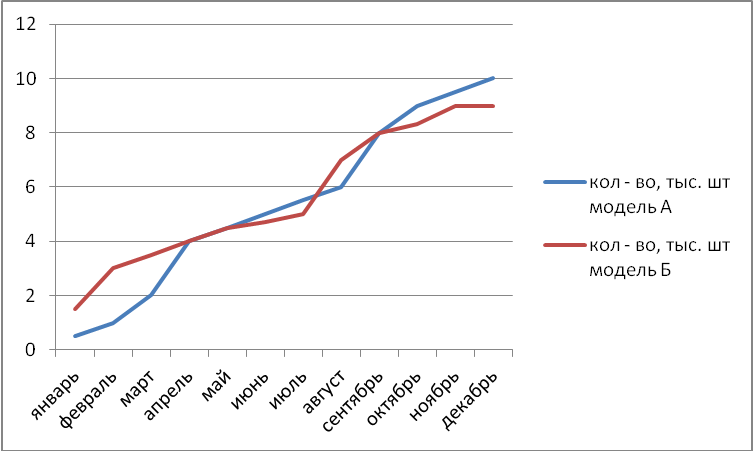 А20. Сколько автомобилей этих двух моделей было продано за последние 4 месяца года? Ответ: ______________________ 2 часть. Алгебра. В1. Решите уравнение: (2х2 – 3)/(х – 2) – (4х – 3)\(х – 2) = 0 В2. Один из катетов прямоугольного треугольника в 4 раза больше другого, а его гипотенуза равна 17. Найдите больший катет. В3. Известно, что 2 ≤ а ≤ 4, 4 ≤ в ≤ 5. Оцените значение выражения а – 3в. Геометрия. В4. Один из углов ромба равен 1200, а диагональ, исходящая из вершины этого угла, равна 10 см. Найдите периметр ромба. В5. Средняя линия трапеции равна 16 см. Найдите основания трапеции, если они относятся как 3:5. В6. Катеты прямоугольного треугольника равны 15 см и 20 см. Найдите их проекции на гипотенузу. |