Учебник для студентов образовательных учреждений спо/С. Г. Григорьев, С. В. Иволгина; под редакцией В. А. Гусева 10-е изд., стер. М.: Издательский центр «Академия». 2014. 416 с
 Скачать 60.25 Kb. Скачать 60.25 Kb. |
Методические указания по проведениюпрактической работы № 7Действия с матрицамиЦель работы: Используя теоретический материал и образцы решения задач, решить примеры по теме «Действия с матрицами» Перечень справочной литературы :
Краткие теоретические сведения: Матрицей называется прямоугольная таблица чисел, состоящая из m строк и n столбцов, которую записывают в следующем виде: 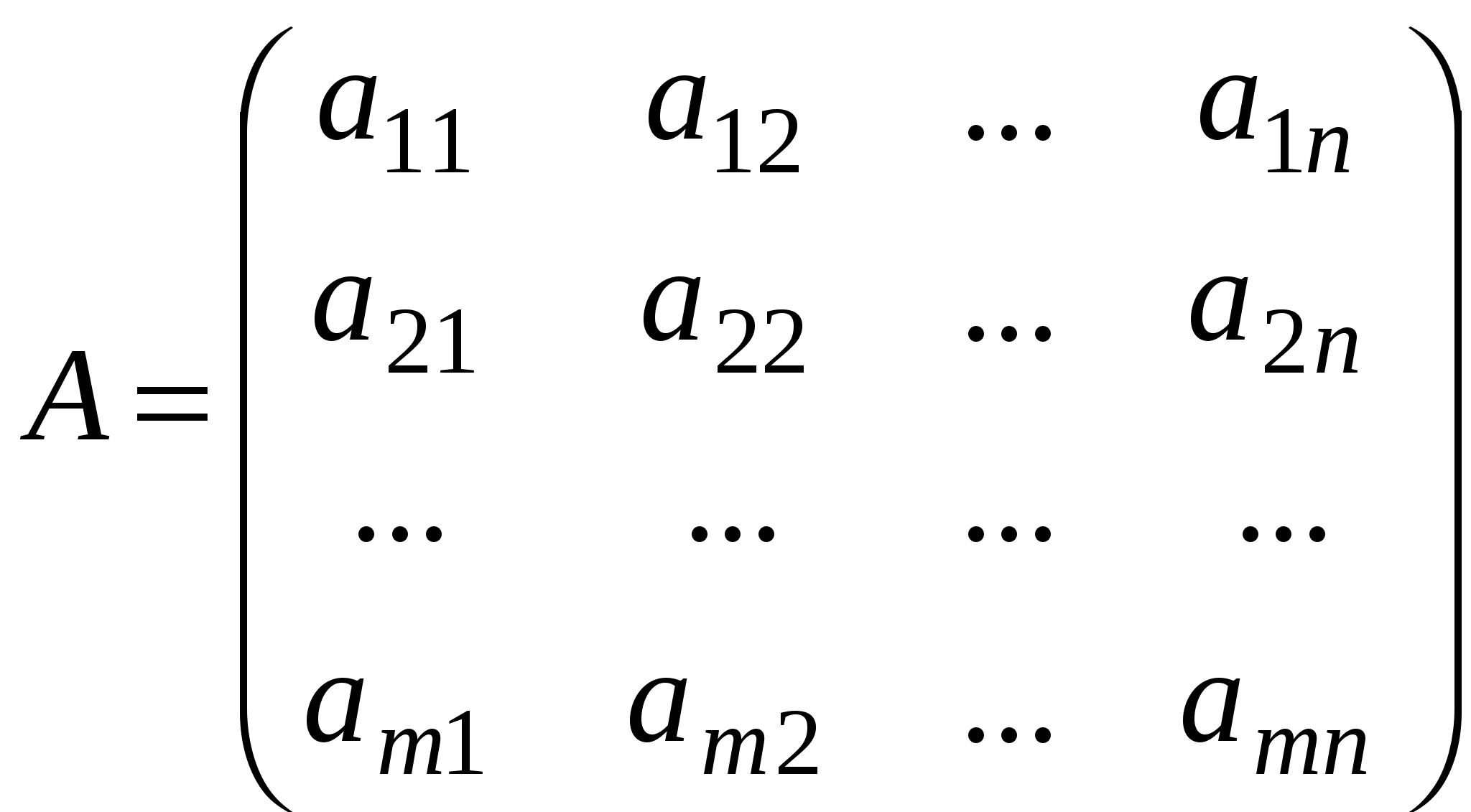 . .Для обозначения матрицы используют прописные латинские буквы, для обозначения элементов матрицы – строчные латинские буквы с указанием номера строки и столбца, на пересечении которых стоит данный элемент. Запись « матрица B имеет размер mxn» означает, что речь идет о матрице, состоящей из m строк и n столбцов. Например, матрица При ссылке на i-ю строку матрицы A используют обозначение Ai, при ссылке на j-й столбец – обозначение Aj. Матрица, у которой число строк совпадает с числом столбцов, называется квадратной. Элементы a11 , a22 ,…, ann квадратной матрицы A (размера nxn) образуют главную диагональ. Квадратная матрица, у которой отличные от нуля элементы могут стоять только на главной диагонали, называется диагональной. Диагональная матрица, у которой все элементы (главной диагонали!) равны 1, называется единичной. Наконец, квадратная матрица, у которой ниже (выше) главной диагонали находятся только нули, называется верхней (нижней) треугольной матрицей. Например, среди квадратных матриц размера 3x3 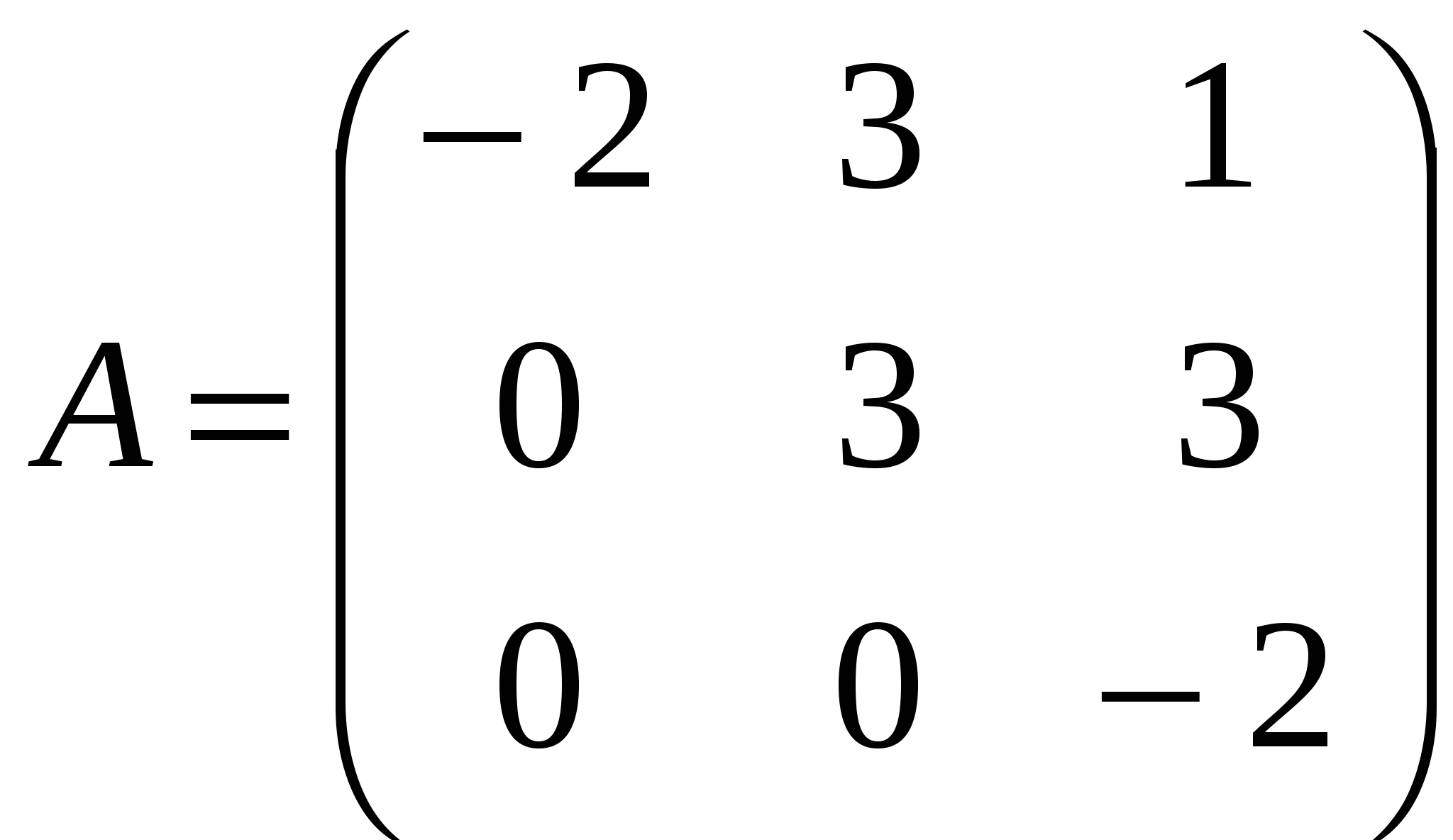 , ,  , ,  , , 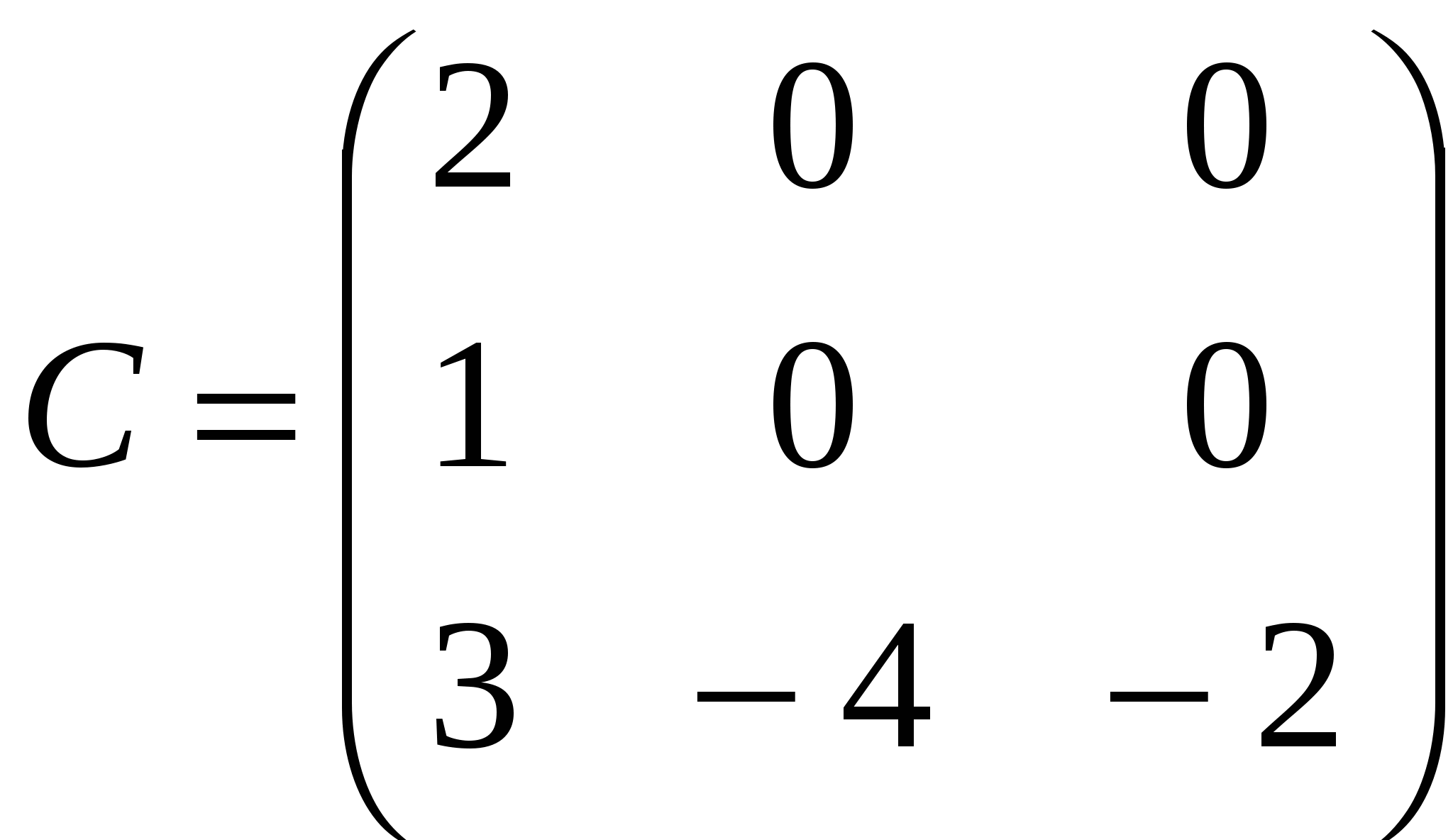 матрица A является верхней треугольной, B – диагональной, C – нижней треугольной, E – единичной. Матрицы A, B называются равными (A=B), если они имеют одинаковый размер, и их элементы, стоящие на одинаковых позициях, совпадают. Арифметические действия с матрицами. Чтобы умножить матрицу A на отличное от нуля вещественное число k, необходимо каждый элемент матрицы умножить на это число: 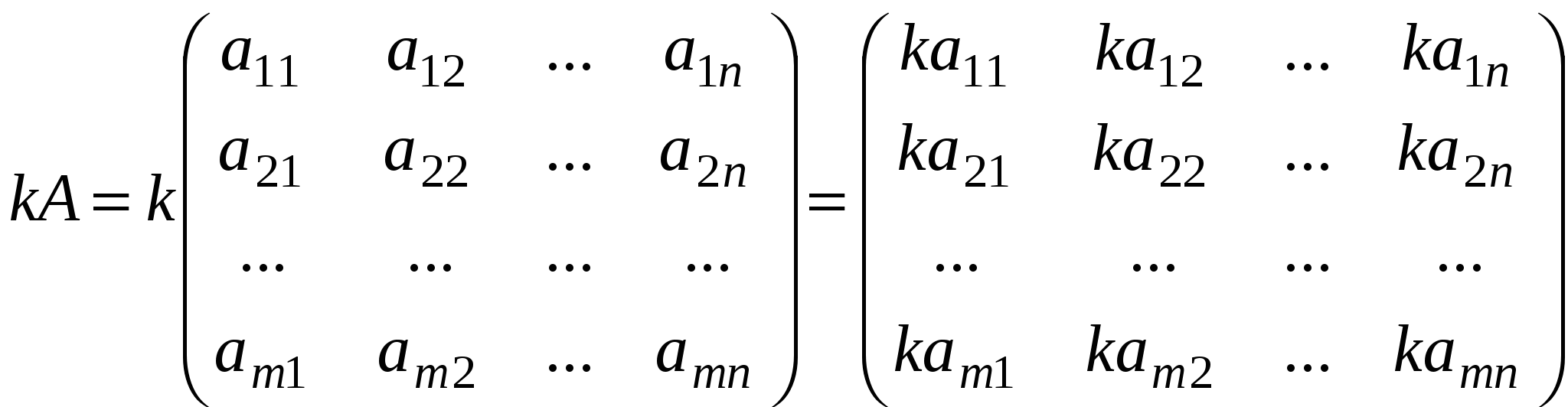 . .Чтобы найти сумму матриц A, B одной размерности, необходимо сложить элементы с одинаковыми индексами (стоящие на одинаковых местах): 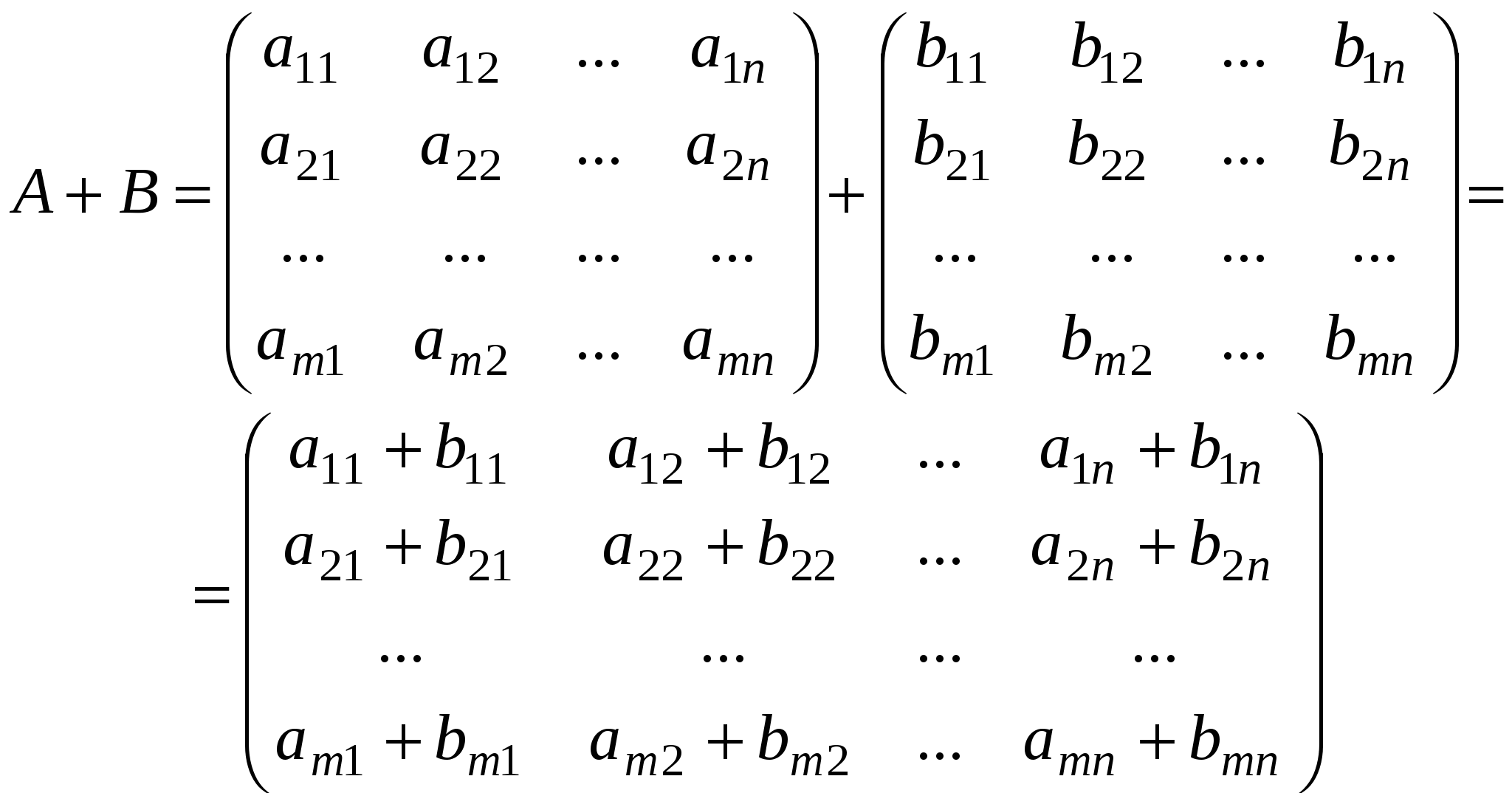 . .Пример 1. Найти 2A-B, если Решение. Сначала умножаем матрицу A на число «2», затем матрицу B на число «-1», и, наконец, находим сумму полученных матриц: Имеем: 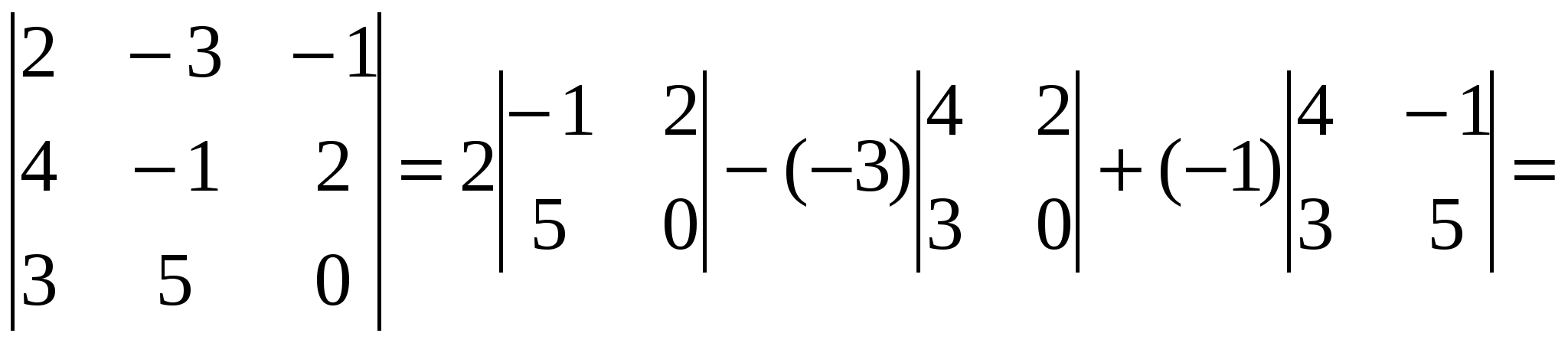 Произведение AB можно определить только для матриц A размера mxn и B размера nxp, при этом AB=C, матрица C имеет размер mxp, и ее элемент cij находится как скалярное произведение i-й строки матрицы A на j-й столбец матрицы B: Пример 2. Найти произведение матриц 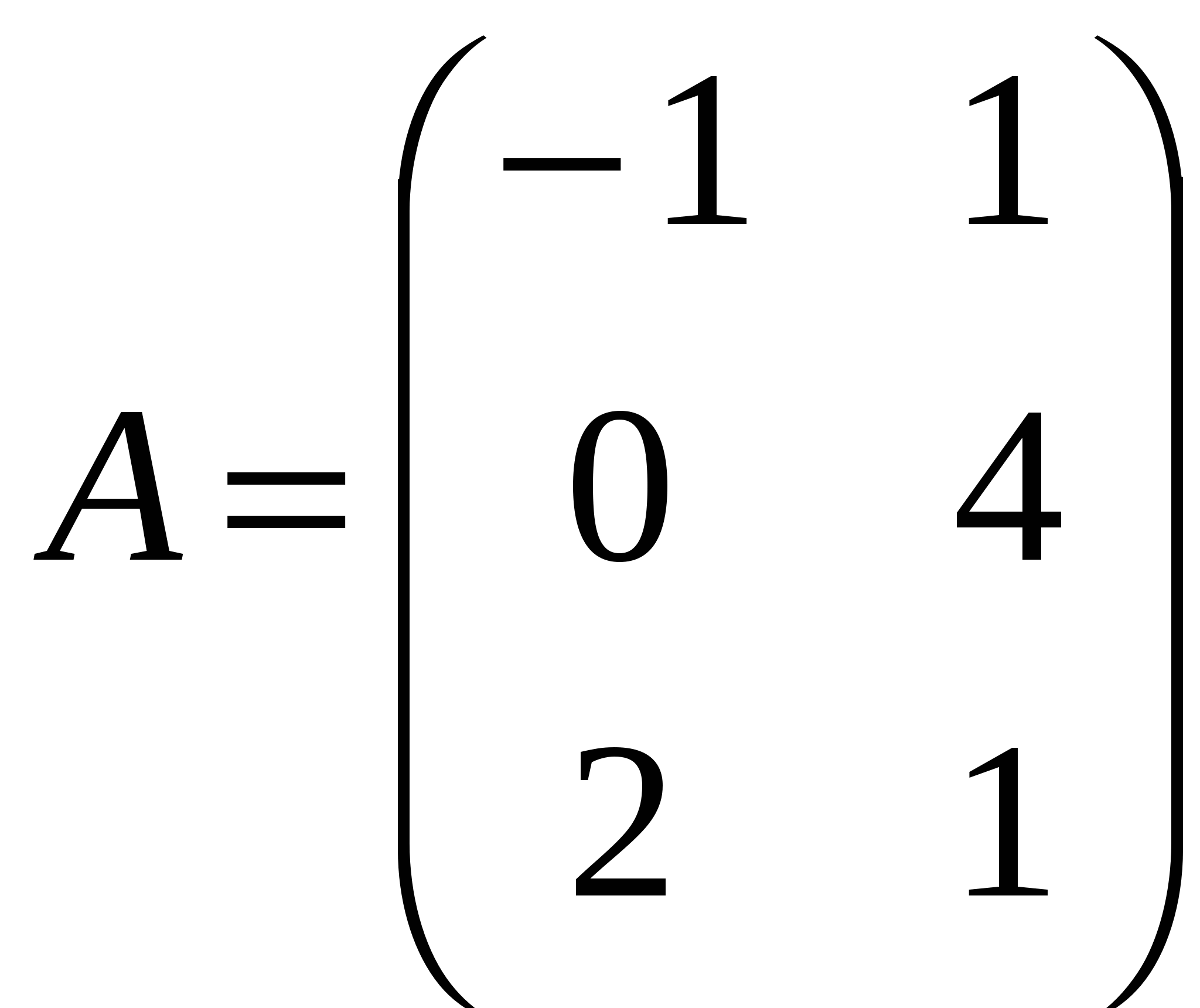 и и Решение. Размер матрицы A 3x2, матрицы В 2х2. Поэтому произведение АВ найти можно, произведение ВА – нет. Действуя по сформулированному выше правилу, получаем: 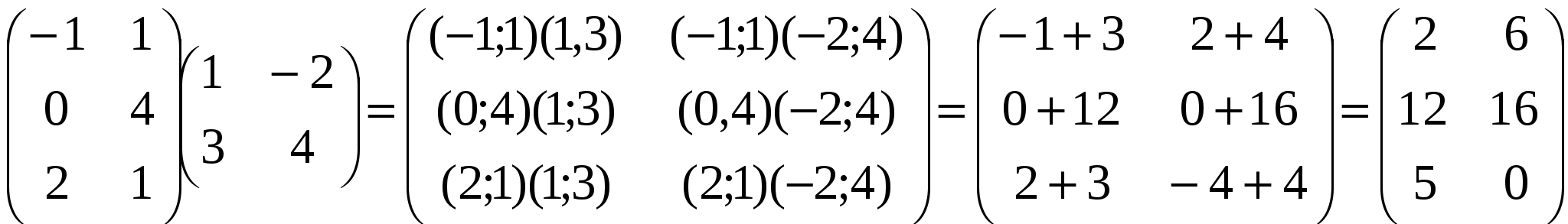 Матрицей, транспонированной к матрице A размера mxn, называется матрица AT размера nxm, строки которой являются столбцами исходной матрицы. Например, если 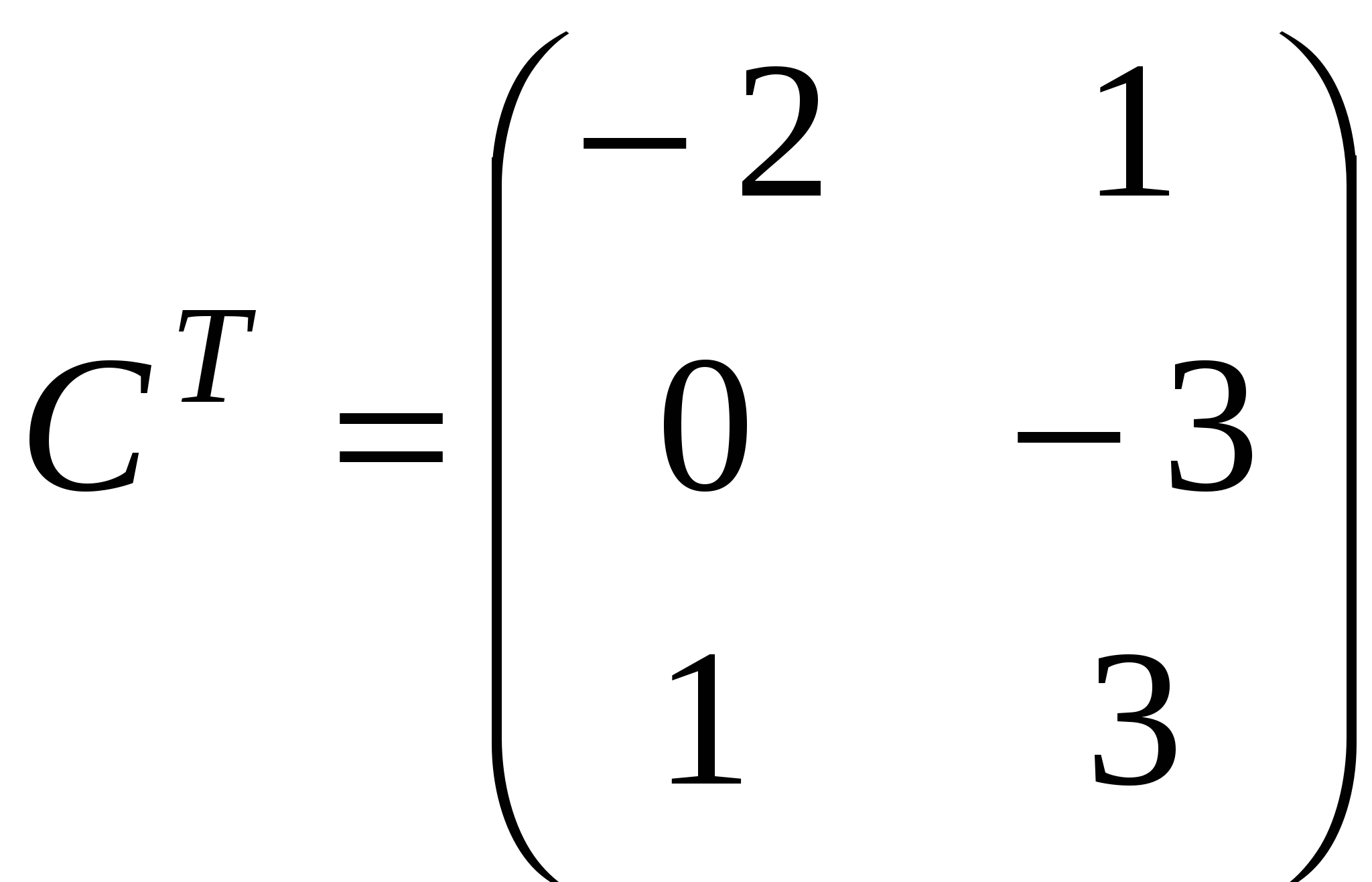 . .Пример 3. Найти 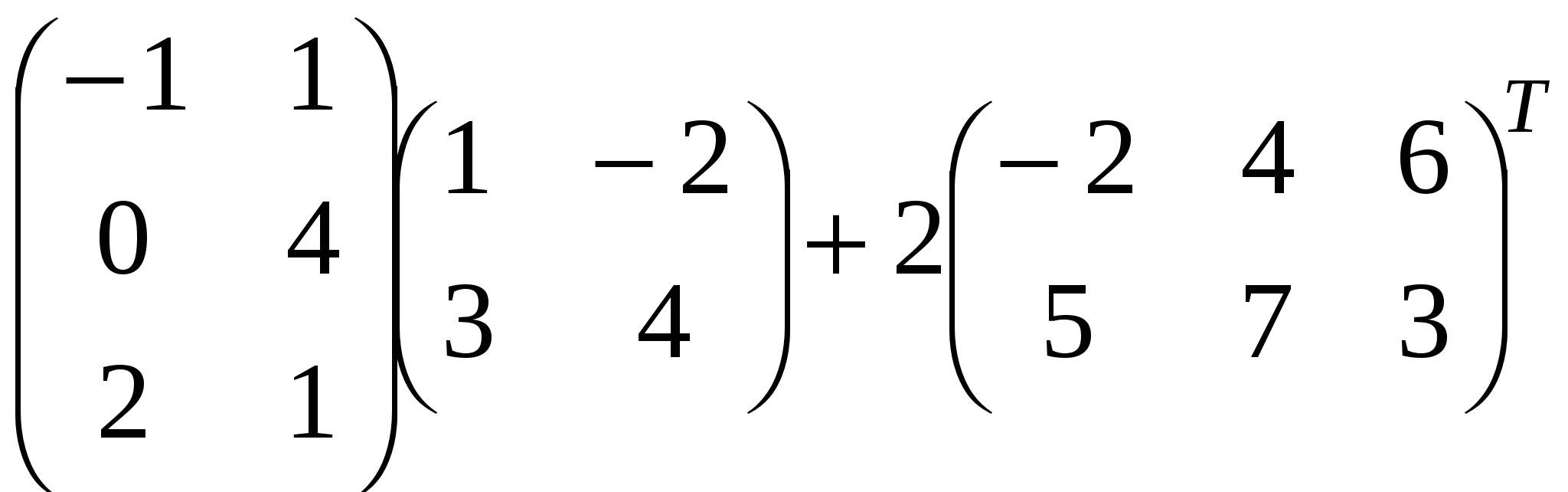 . .Решение. Воспользовавшись вычислениями, проведенными при решении примера, а также правилами умножения матрицы на число и сложения матриц, получим: 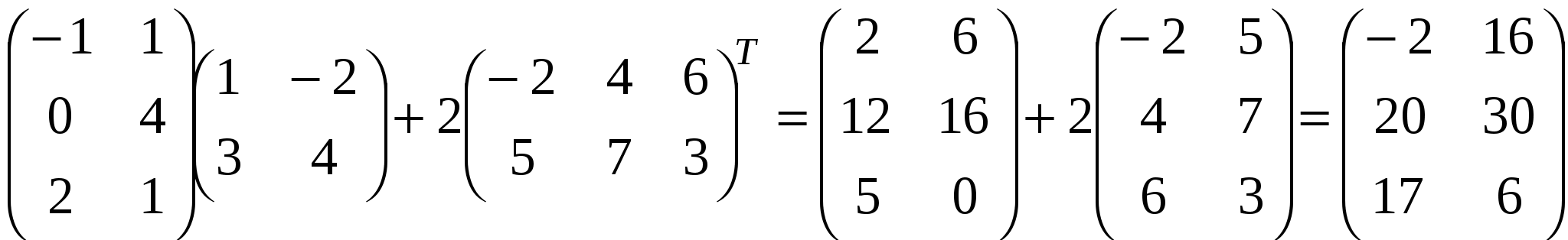 . .Матрицы A, B называются эквивалентными, если одна получена из другой путем элементарных преобразований. Рангом матрицы A в дальнейшем будем считать число строк эквивалентной ей ступенчатой матрицы, используя обозначение r(A). Так, в рассмотренном выше примере 3.4 r(A)=3, r(B)=2. Можно доказать, что ранг матрицы A (размера mxn) не может быть больше 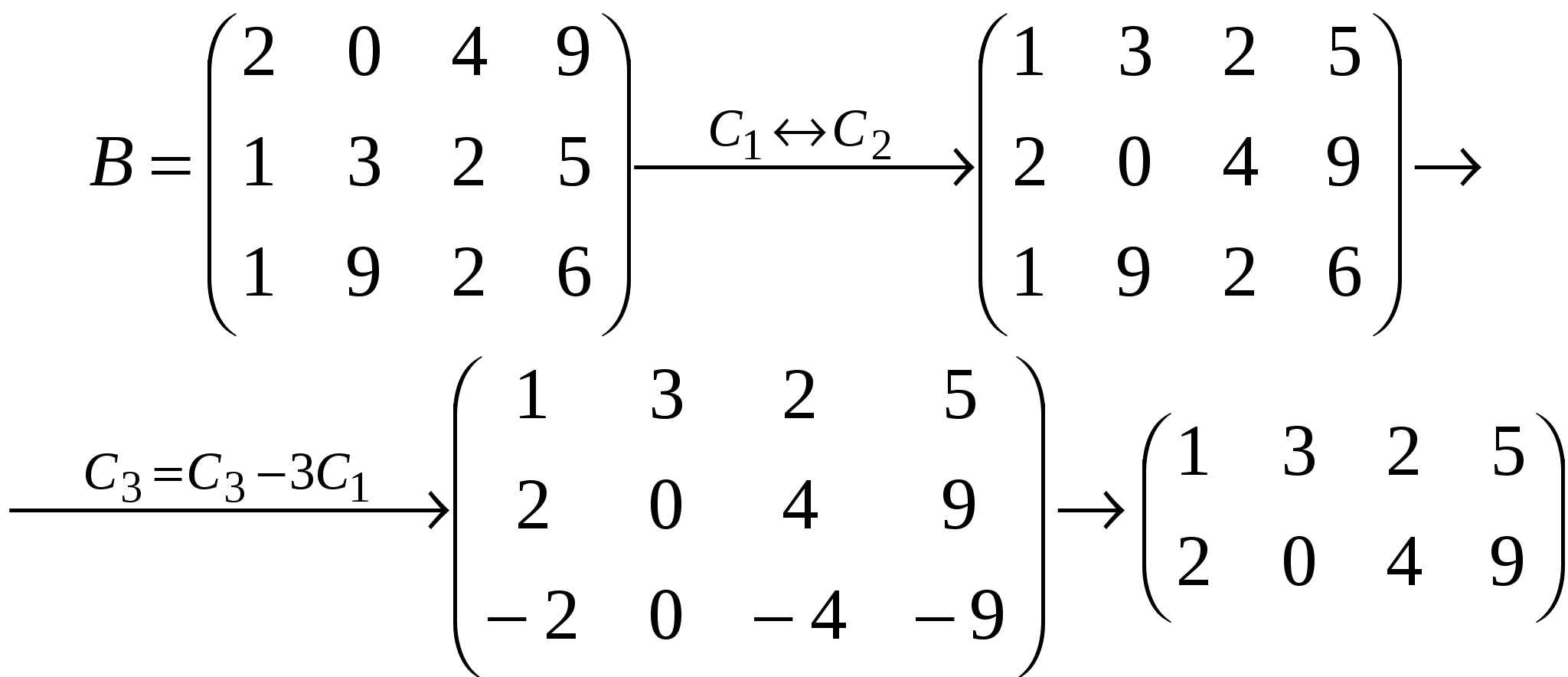 Вычисление определителей. Определитель матрицы A размера 2x2 (определитель 2-го порядка) – это число, которое можно найти по правилу: (произведение элементов, стоящих на главной диагонали матрицы, минус произведение элементов, стоящих на побочной диагонали). Определитель матрицы A размера 3x3 (определитель 3-го порядка) – число, вычисляемое по правилу «раскрытие определителя по первой строке»: 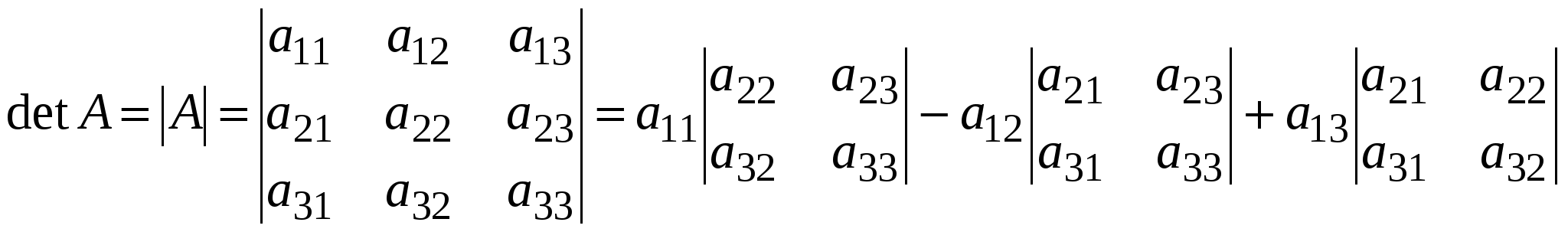 Пример 4. Найти: 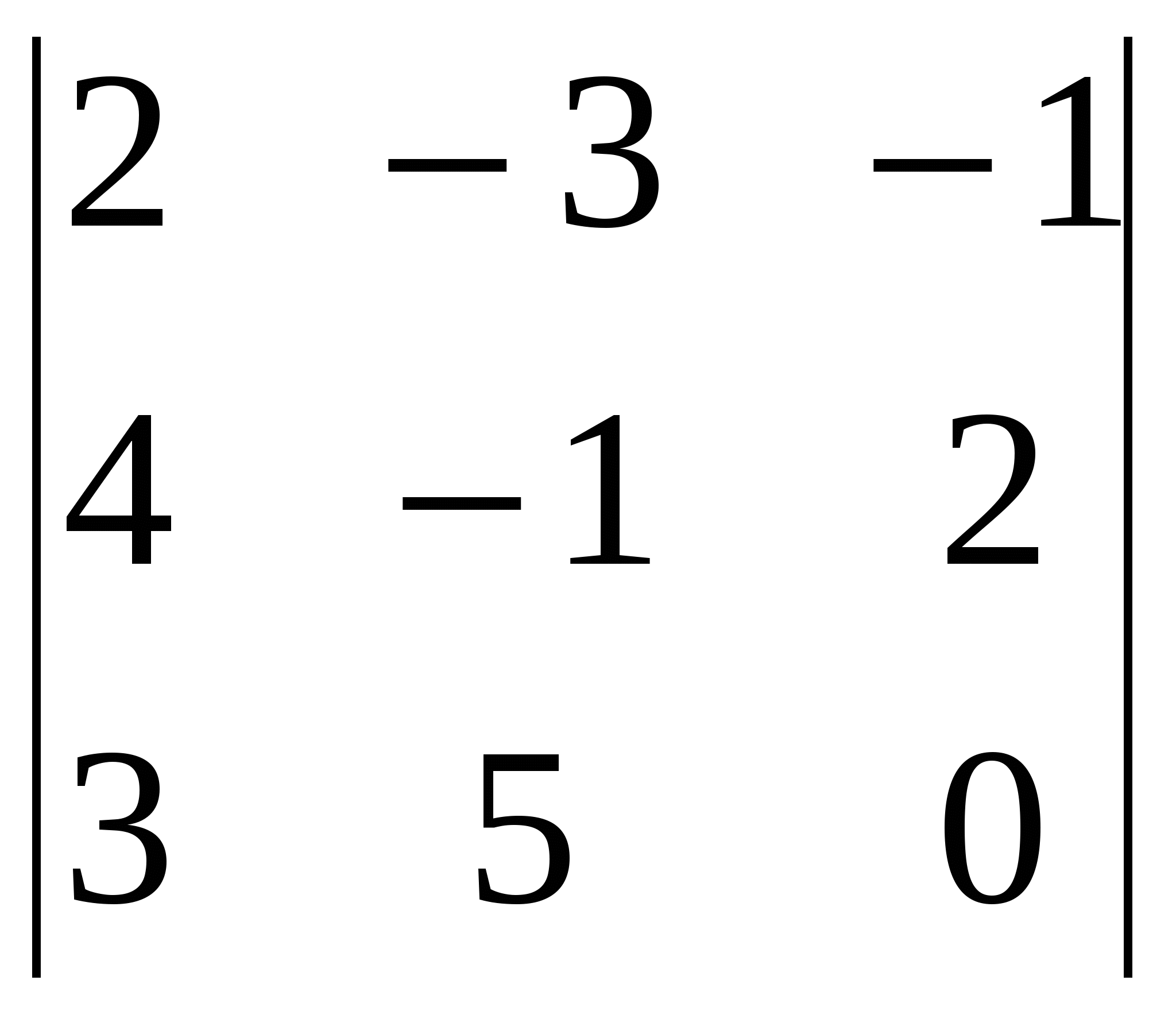 Решение. При нахождении определителя воспользуемся сначала формулой 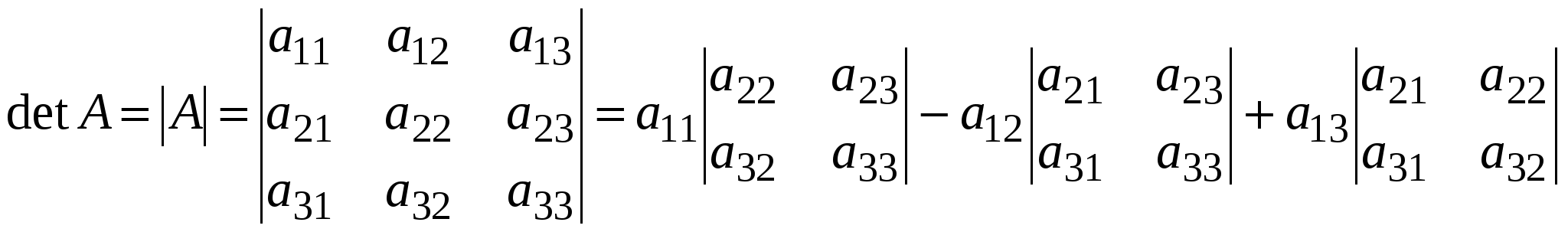 , а затем (для вычисления определителей 2-го порядка) формулой , а затем (для вычисления определителей 2-го порядка) формулой Порядок проведения работы:
Задания Задание 1. Выполнить арифметические действия с матрицами: 1)  ; ; 3) 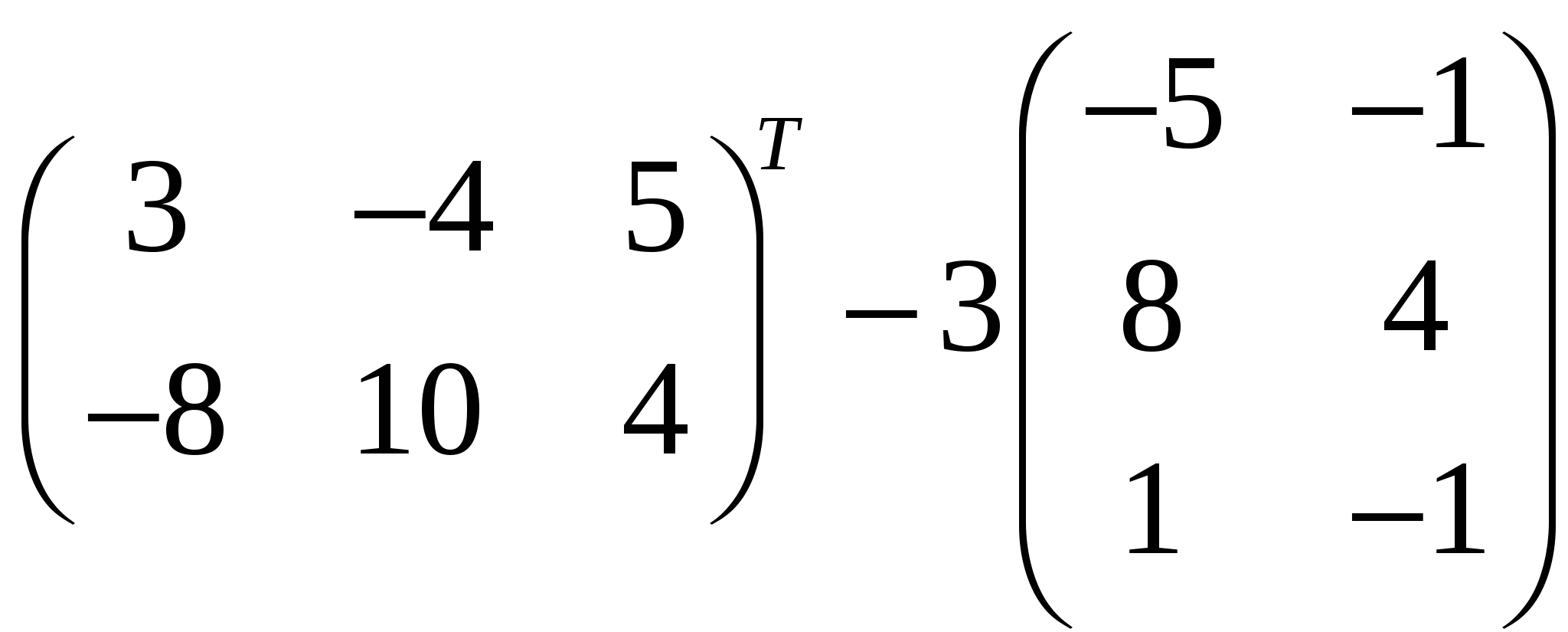 ; 4) ; 4)  ; ;5) 6)  ; ; 7) 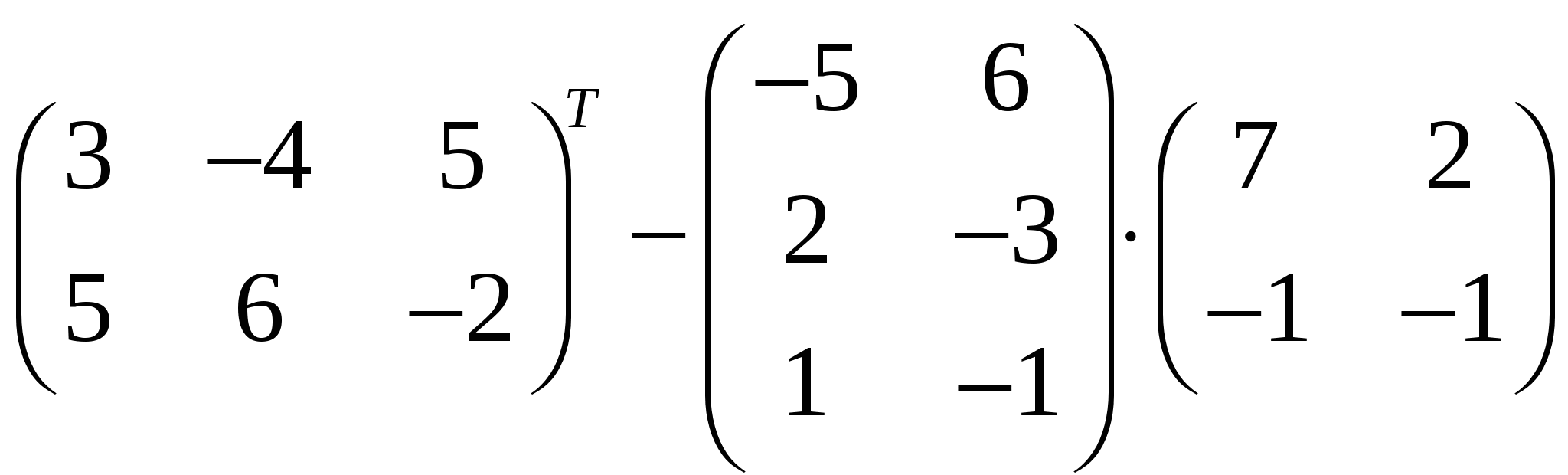 Задание 2. Доказать равенство (AB)C=A(BC) для матриц: 1) 2)  , , 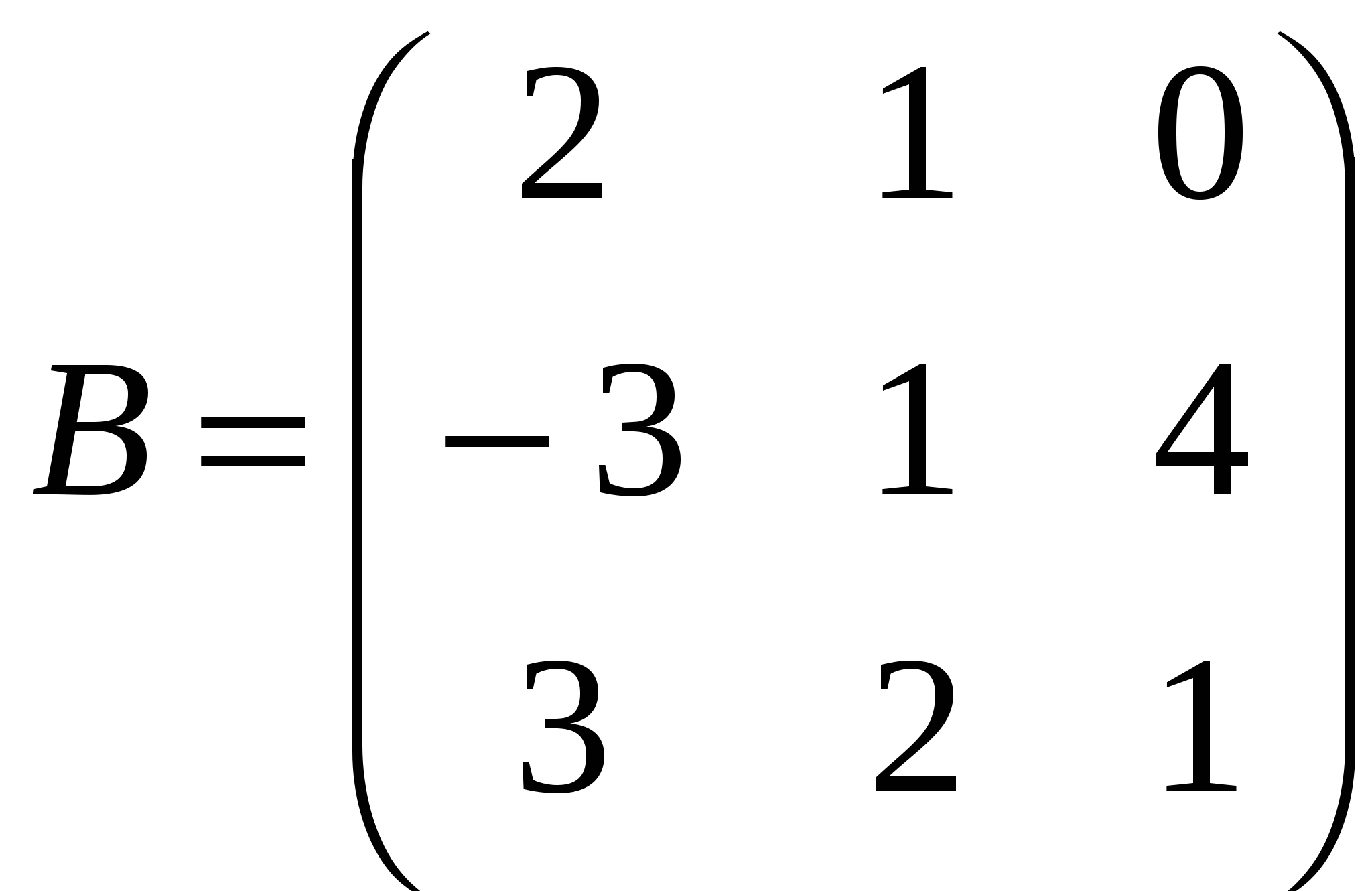 , , 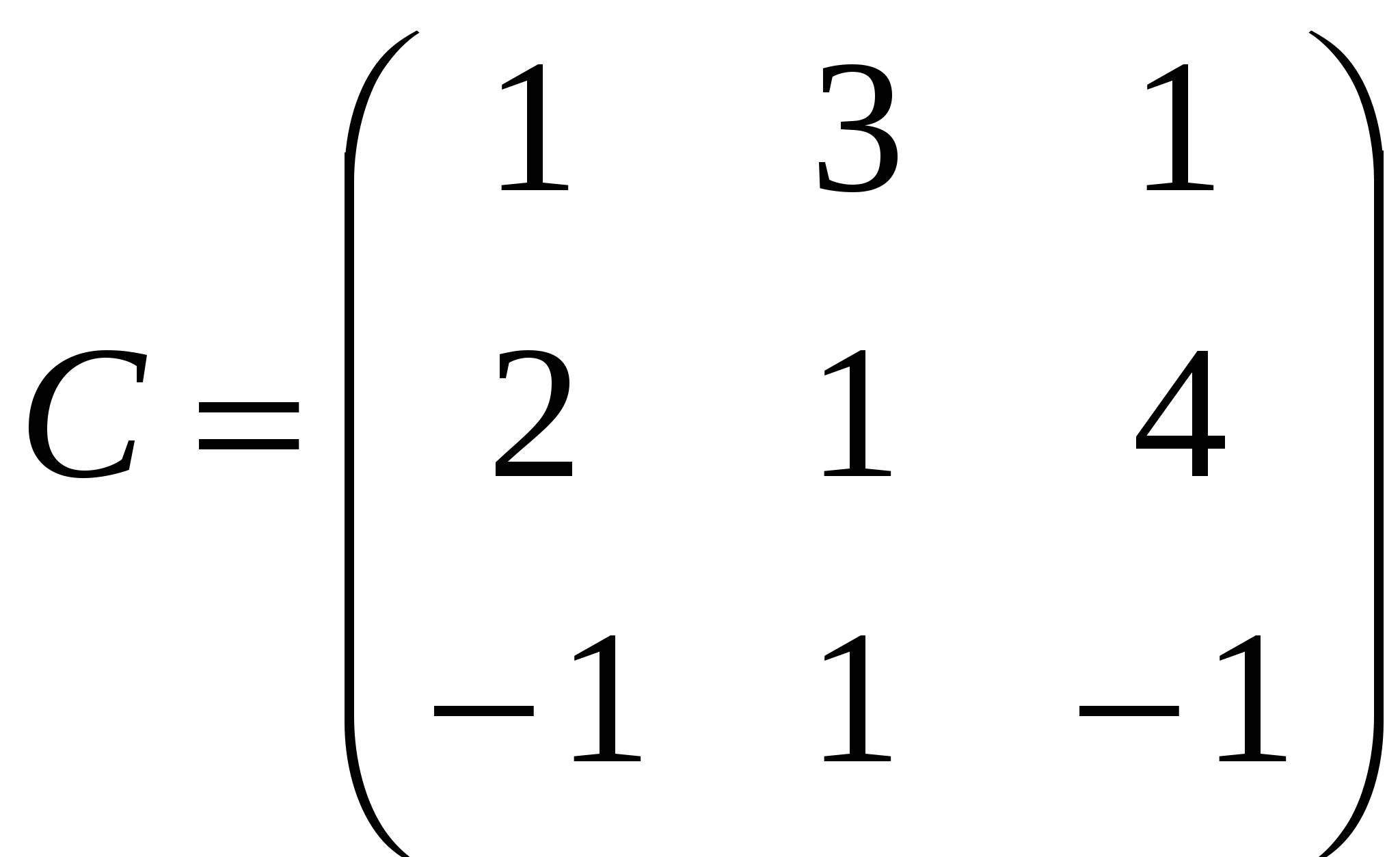 ; ;3)  , , 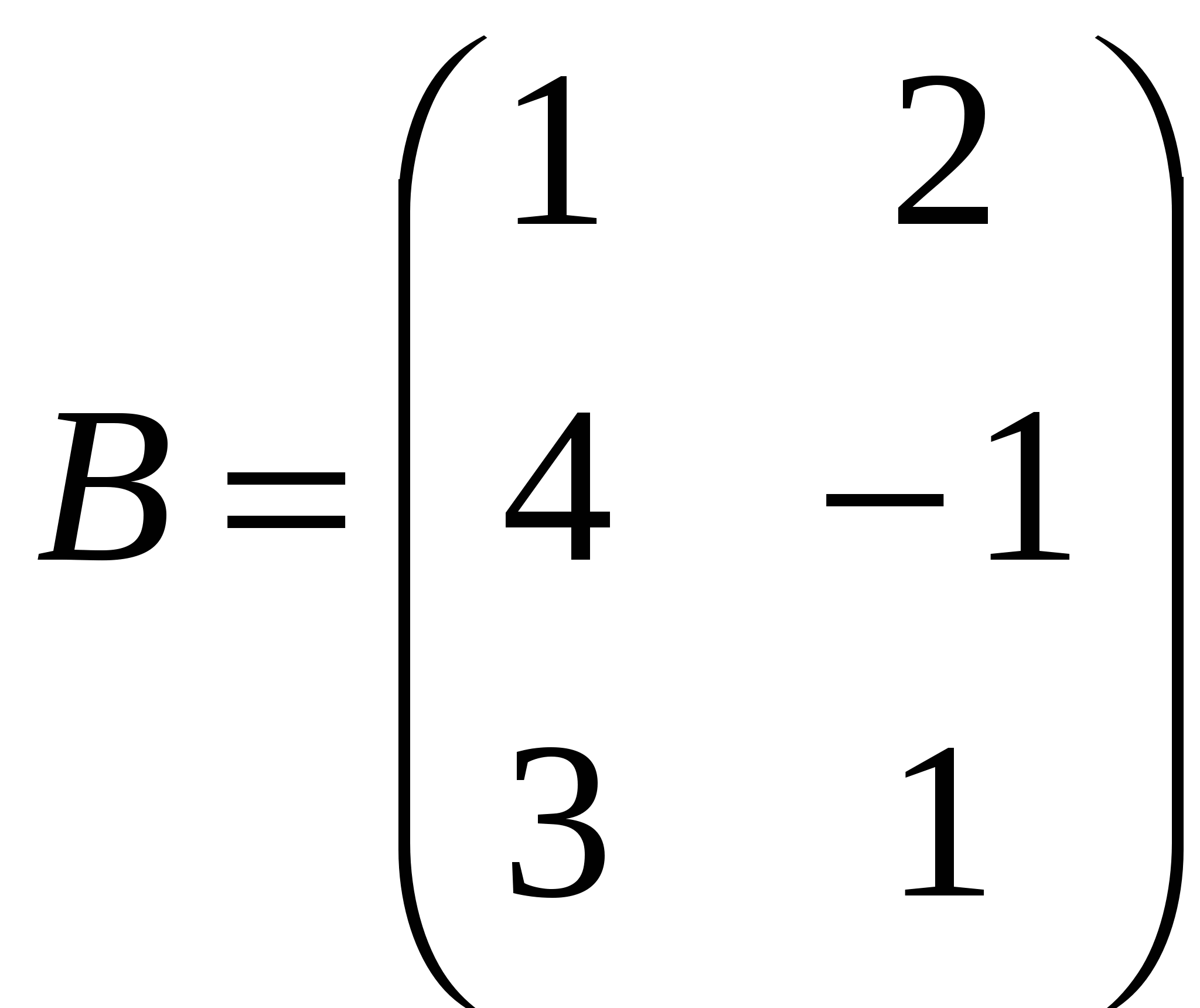 , , Задание 3. Найти: 1)  ; 2) ; 2) 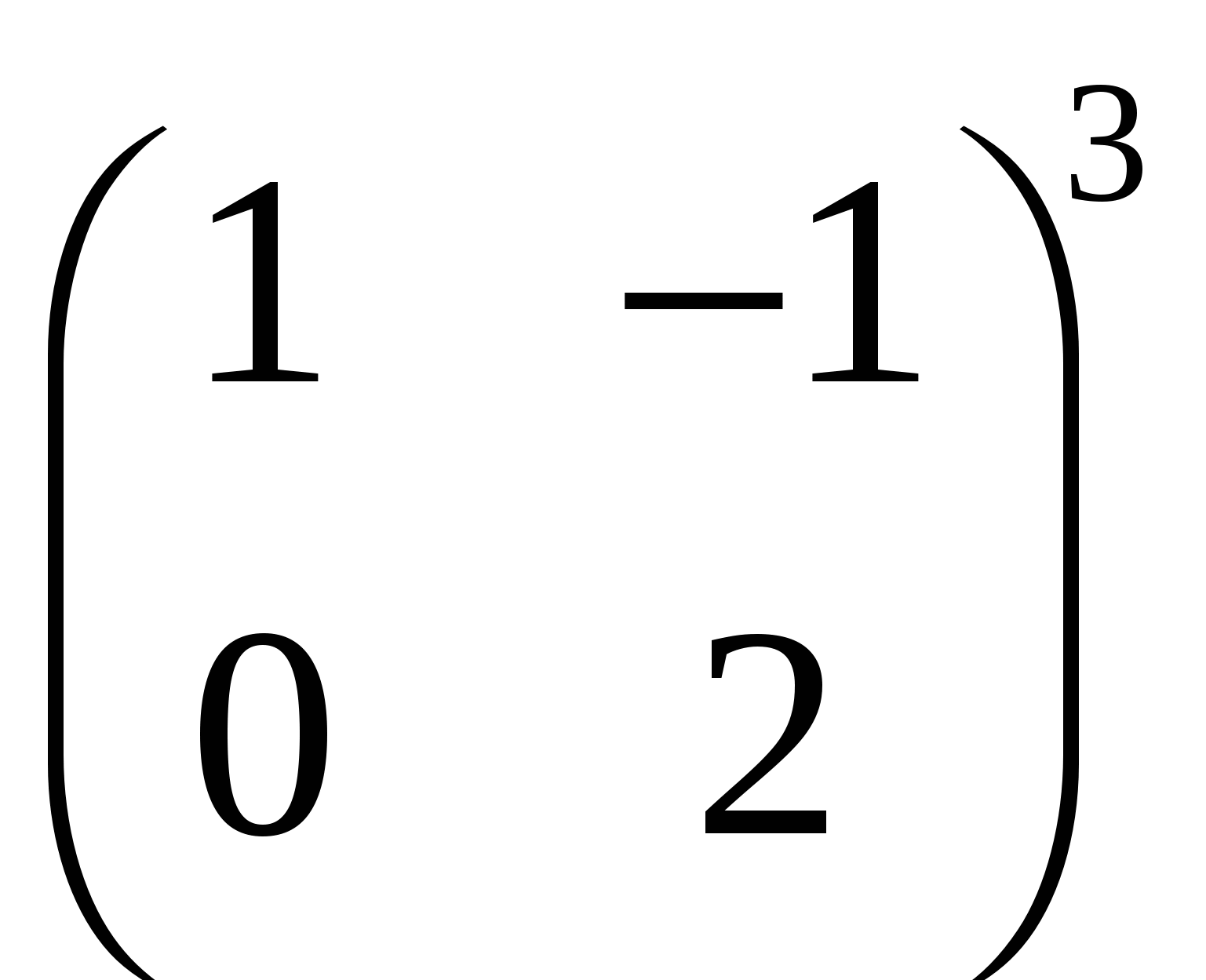 ; 3) ; 3) 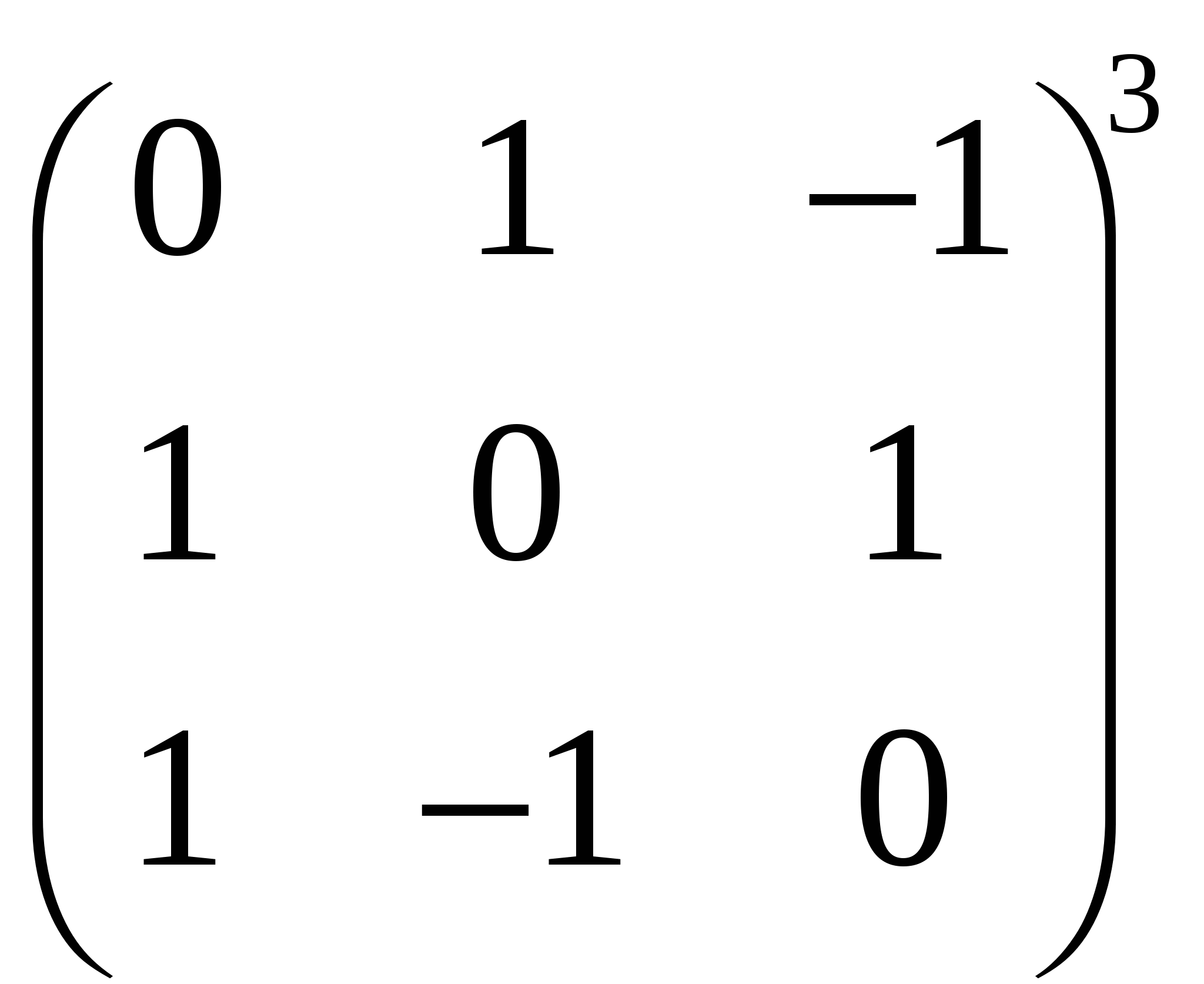 . .Задание 4. Вычислить определители:
|
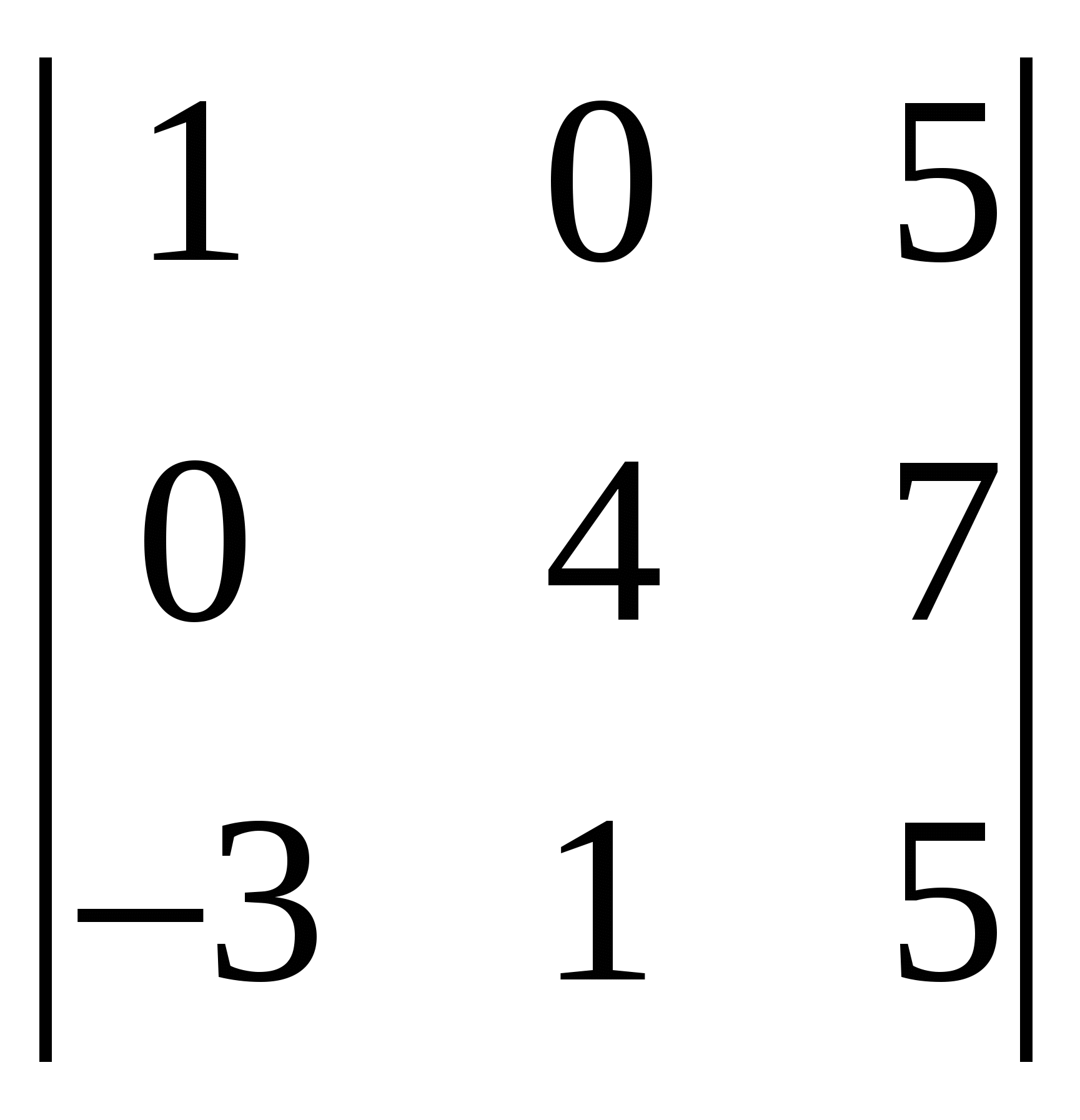
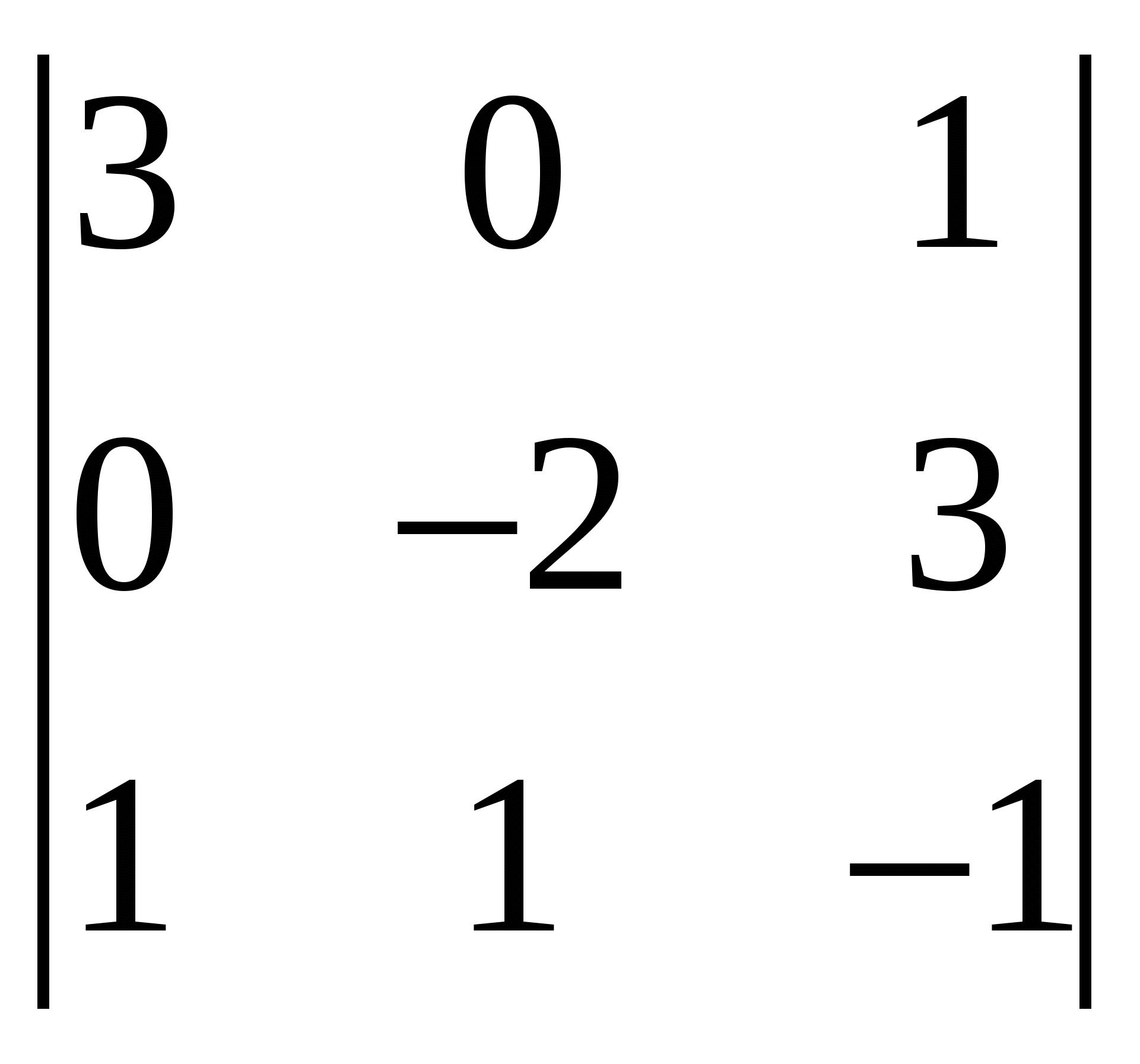 ;
;