Свойства степени с рациональным показателем
 Скачать 33.13 Kb.
|
| А-9 Декабрь 2014 г . Тема урока: Свойства степени с рациональным показателем. Цель урока: Повторить определение степени с рациональным показателем и свойства степени с рациональным показателем Ход урока: 1. Организационный момент. 2. Актуализация целей урока. Цель нашего урока - повторить определение и свойства степени с рациональным показателем, применение свойств при решении упражнений. 3. Вспомним теорию (слайд 1) .   1) Определение. Арифметическим корнем n – ой степени (n N, n 2) из неотрицательного числа a называется такое неотрицательное число, n – я степень которого равна а.   2) Определение. (слайд32) Степень с рациональным показателем   Если 3) Свойства степени с рациональным показателем (слайд 3):  При a > 0, b > 0, p и q - рациональные числа: а) ; в) ;   б) г) ;  ;д) . 4. Тренировочные упражнения (слайд 4) . 1) Базовый уровень.  №1. Вычислить.Ответ. -26,5.  №2. Найдите значение выражения. Ответ. -2.  №3. Упростите выражение. Ответ. 1. №4. Найдите значение выражения. 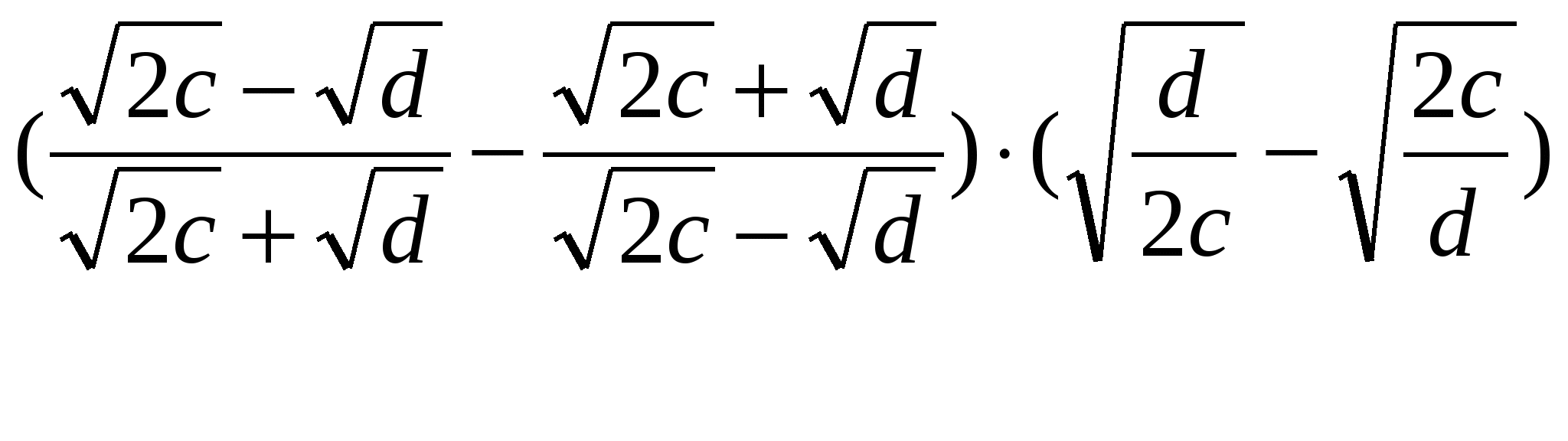 Ответ. 4.  №5. Упростить выражение  Ответ. .1) Повышенный уровень (слайд 4) .  №6. Упростить выражение Ответ. 2. Указание. Преобразовать подкоренные выражения, воспользоваться формулами сокращённого умножения (квадрат суммы и квадрат разности). 5. Задания для самостоятельной работы с последующей проверкой (слайд 5) .  Вычислить: 1) ;  2) ;   3) ;4) ;  5) ;  Упростить: 6) ; 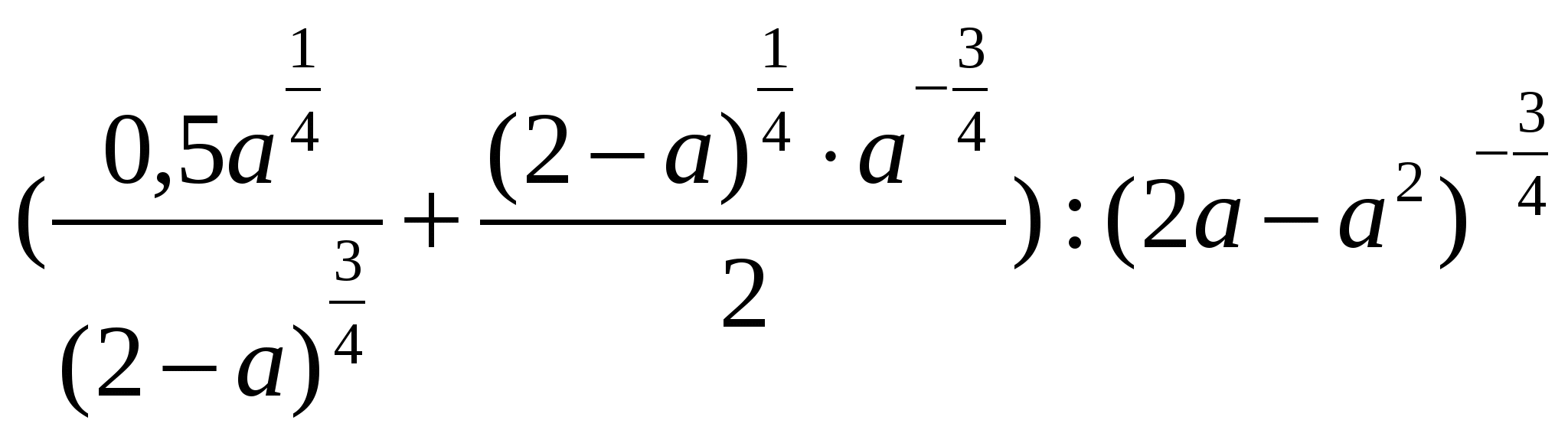 7) .   5) (слайд 8)  Указание. Использовать формулу разности кубов ;  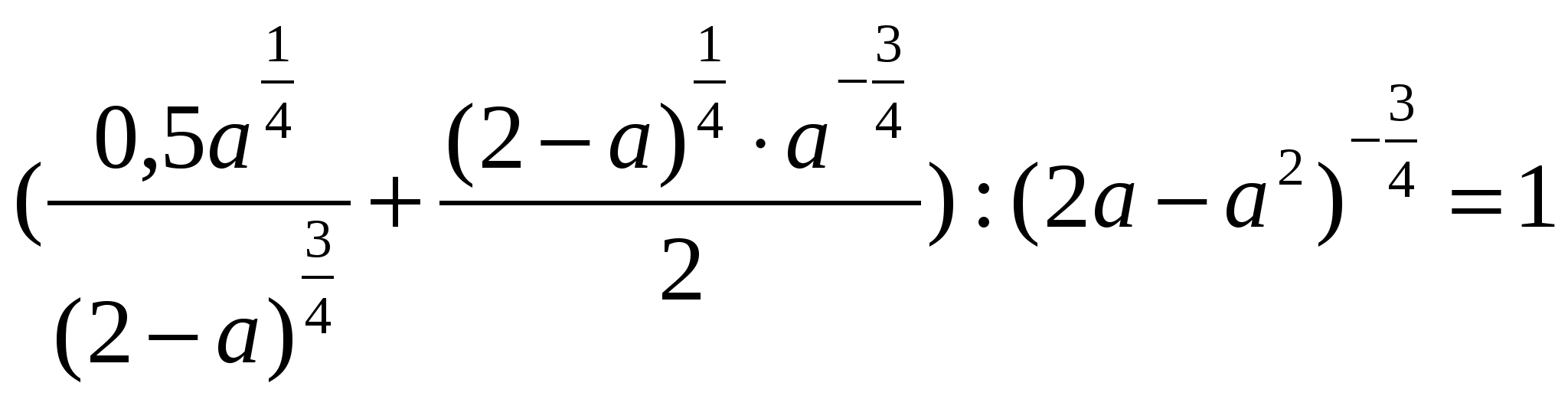6) ;  7) (слайд 5) 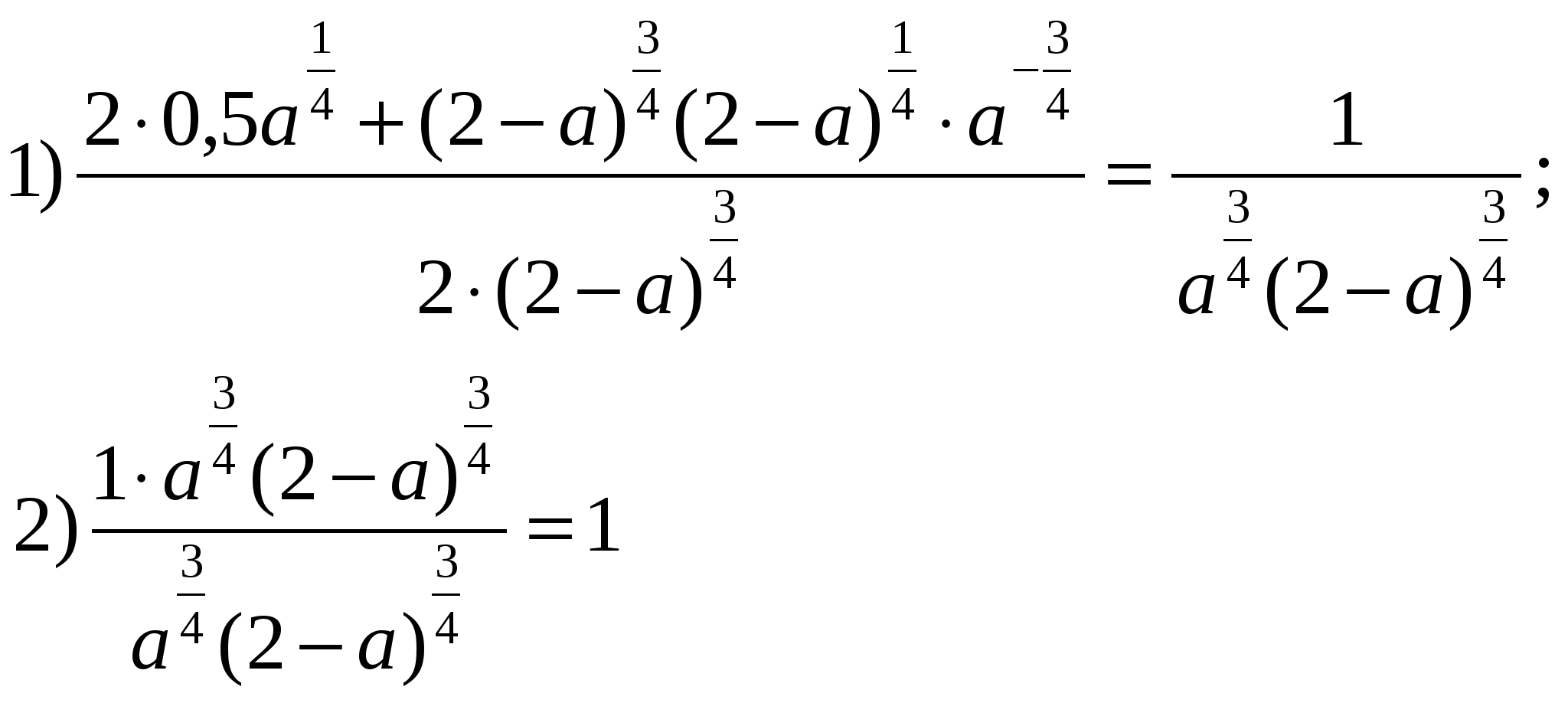 6. Подведение итогов урока. Повторение изученных свойств, выставление оценок. 7. Задание на дом. (слайд 6) Тренировочный тест по теме «Свойства степени с рациональным показателем» (поверка на следующем уроке). (слайд7) 1. Найдите значение выражения:  1) 12; 2) 6; 3) 3; 4) –3. 2. Выберите верное неравенство: 1)  2)  3)  4) 3-8 < 0.3. Среди данных чисел выберите наибольшее: 1) 5  ;  2) 5 ; 3) 5 ; 4) 5 . 4. Представьте данное выражение в виде степени:  . 1) у -3; 2) у -7,14; 3) у 3; 4) у 6. 5. Упростите выражение:  . 1)  2)  3)  4)  (слайд 8) 6. Упростите выражение: (а-1,5)  . 1) а; 2) а  ; 3) а  ; 4)  7. Найдите значение выражения:  1)  2) 1,2 3)  4)  8. Найдите значение выражения:  1) -4; 2) 9; 3) -5; 4) 5. 9. Сократите дробь:  1)  2)  3)  4)  10. Найдите значение выражения: 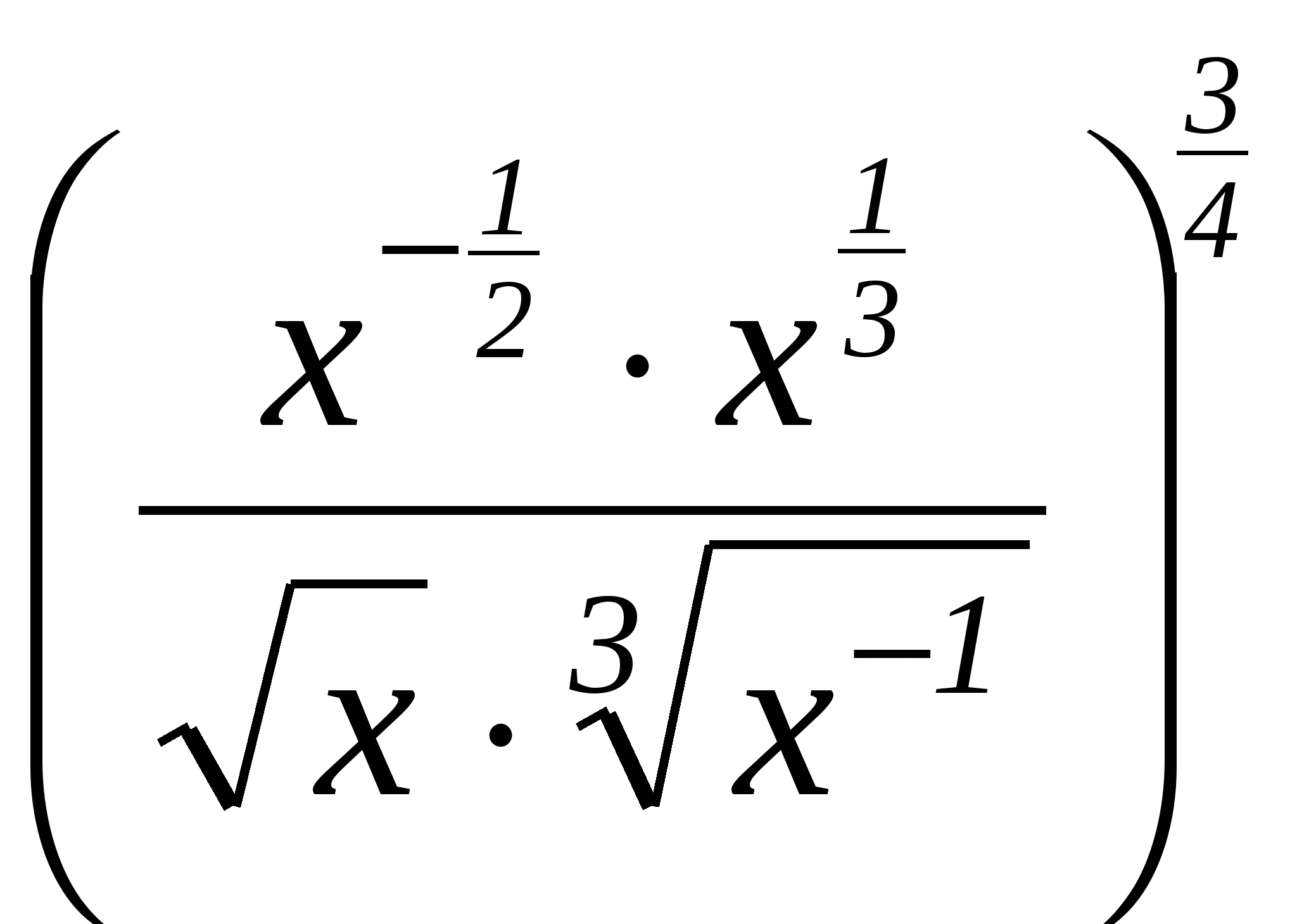 при х = 0,0625. 1) 0,5; 2) 2; 3) 4; 4) 0,25. |