Разбор задачи A5 (демо егэ 2013)
 Скачать 53.2 Kb. Скачать 53.2 Kb.
|
Разбор задачи A5 (демо ЕГЭ 2013)Автомат получает на вход два двузначных шестнадцатеричных числа. В этих числах все цифры не превосходят цифру 6 (если в числе есть цифра больше 6, автомат отказывается работать). По этим числам строится новое шестнадцатеричное число по следующим правилам.
Пример. Исходные числа: 66, 43. Поразрядные суммы: A, 9. Результат: 9A. Определите, какое из предложенных чисел может быть результатом работы автомата.
Решение: Введем обозначения:
Ограничения исходя из условия задачи:
Рассмотрим предлагаемые варианты чисел. 9F-не подходит, т.к. сумма разрядов =F, a F>C. 911-не подходит, т.к. сумма разрядов =11, a 11>C. 42-не подходит, т.к. числа записаны в порядке убывания, а не возрастания. 7A-подходит. Получили число: 7A. Разбор задачи A5 (демо ЕГЭ 2012)Время выполнения-2 мин, уровень сложности-базовый Автомат получает на вход два трехзначных числа. По этим числам строится новое число по следующим правилам. 1. Вычисляются три числа – сумма старших разрядов заданных трехзначных чисел, сумма средних разрядов этих чисел, сумма младших разрядов. 2. Полученные три числа записываются друг за другом в порядке убывания (без разделителей). Пример. Исходные трехзначные числа: 835, 196. Поразрядные суммы: 9, 12, 11. Результат: 12119 Определите, какое из следующих чисел может быть результатом работы автомата.
Решение: Рассмотрим предлагаемые варианты чисел. 151303-не подходит, т.к. сумма разрядов представлена не как "3", а как "03",т.е добавлен незначащий 0. 161410-подходит. 191615-не подходит,т.к. сумма разрядов не может быть >18. 121613-не подходит, т.к. числа не записаны в порядке убывания. Получили число: 161410. Разбор задачи A7 (демо ЕГЭ 2011)Время выполнения-2 мин, уровень сложности-базовый Лена забыла пароль для входа в Windows XP, но помнила алгоритм его получения из символов «A153B42FB4» в строке подсказки. Если последовательность символов «В4» заменить на «B52» и из получившейся строки удалить все трехзначные числа, то полученная последовательность и будет паролем:
Решение: A 1 5 3 B 4 2 F B 4 -нашли "B4". A 1 5 3 B 5 2 2 F B 5 2 - заменили "B4" на "B52". A 1 5 3 B 5 2 2 F B 5 2 - нашли трехзначные числа. A B F B 5 2 - удалили трехзначные числа. Получили пароль: A B F B 5 2. Разбор задачи B6 (демо ЕГЭ 2013)Алгоритм вычисления значения функции F(n), где n – натуральное число, задан следующими соотношениями: F(1) = 1 F(n) = F(n–1) * n, при n >1 Чему равно значение функции F(5)? В ответе запишите только натуральное число. Ответ: 120 Решение: Это задача на знание рекурсии. 1 способ F(1) = 1 F(2) = F(1)*2 F(3) = F(2)*3 F(4) = F(3)*4 F(5) = F(4)*5=F(3)*4*5=F(2)*3*4*5=F(1)*2*3*4*5=1*2*3*4*5=24*5=120 2 способ (быстрый, если разобраться) Функция F(n) - это факториал числа n, т.е. F(n)=n! Рассмотрим, почему данный алгоритм описывает поиск факториала. Рекурентная формула факториала имеет вид:  Подставляя вместо n! F(n) и учитывая, что мы начали с n=1, получим формулу: 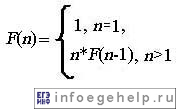 А это и есть алгоритм, приведенный в задании. Поэтому данная задача сводится к поиску факториала числа 5: 5! Факториал вычисляется следующим образом (упрощенный вид): n!=1*2*...*n. Подставляя значение 5 вместо n, получим: 5!=1*2*3*4*5=120. Получили, F(n)=120. Разбор задачи B8 (демо ЕГЭ 2011)Время выполнения-8 мин, уровень сложности-повышенный Строки (цепочки символов латинских букв) создаются по следующему правилу. Первая строка состоит из одного символа – латинской буквы «А». Каждая из последующих цепочек создается такими действиями: в очередную строку сначала записывается буква, чей порядковый номер в алфавите соответствует номеру строки (на i-м шаге пишется i-я буква алфавита), к ней слева дважды подряд приписывается предыдущая строка. Вот первые 4 строки, созданные по этому правилу: (1) A (2) AAB (3) AABAABC (4) AABAABCAABAABCD Латинский алфавит (для справки): ABCDEFGHIJKLMNOPQRSTUVWXYZ Имеется задание: «Определить символ, стоящий в n-й строке на позиции 2n–1– 5, считая от левого края цепочки». Выполните это задание для n = 8. Ответ: С Решение: Определим позицию искомого символа: 2n–1– 5=28-1-5=27-5=128-5=123. Введем обозначение: "AABAABCAABAABCD"-(). Распишем, какие будут созданы строки с 5-го по 8-й шаг. (5) ()()E (6)()()E ()()E F (7) ()()E()()EF ()()E()()EF G (8) ()()E()()EF()()E()()EFG ()()E()()EF()()E()()EFG H Чтобы определить позиции символов, нужно определить сколько символов образуется на каждом шаге. Количество символов определяется по формуле: Ni=2i-1, где i-шаг. На 7-м шаге образуется N7=27-1=127 символа: (7) ()()E()()EF ()()E()()EF G127 На 8-м шаге образуется N8= 28-1=255 символов. Нам нужно найти 123 позицию. До 127 позиции символов на 7-м и 8-м шаге одинаковы: (7) ()()E()()EF ()()E()()EF G (8) ()()E()()EF()()E()()EFG ()()E()()EF()()E()()EFG H Поэтому будем смотреть по 7-му шагу. Так проще,т.к. там меньше элементов. Определим позиции элементов, близкие к искомому: (7) ()()E()()EF ()()E()()E125F126 G127 Получается,что элемент в позиции 123 нужно смотреть в (): (4) AABAABCAABAABC123D124 Получили:С. Разбор задачи B8 (демо ЕГЭ 2010)Уровень сложности-повышенный Строки (цепочки латинских букв) создаются по следующему правилу. Первая строка состоит из одного символа – латинской буквы «А». Каждая из последующих цепочек создается такими действиями: в очередную строку сначала записывается буква, чей порядковый номер в алфавите соответствует номеру строки (на i-м шаге пишется «i»-я буква алфавита), к ней слева дважды подряд приписывается предыдущая строка. Вот первые 4 строки, созданные по этому правилу: (1)A (2)AAB (3)AABAABC (4)AABAABCAABAABCD Латинский алфавит (для справки): ABCDEFGHIJKLMNOPQRSTUVWXYZ Запишите шесть символов подряд, стоящие в седьмой строке со 117-го по 122-е место (считая слева направо). Ответ: AABAAB Решение: Введем обозначение: "AABAABCAABAABCD"-(). Распишем, какие будут созданы строки с 5-го по 7-й шаг. (5) ()()E (6)()()E ()()E F (7) ()()E()()EF ()()E()()EF G Чтобы определить позиции символов, нужно определить сколько символов образуется на каждом шаге. Количество символов определяется по формуле: Ni=2i-1, где i-шаг. На 6-м шаге образуется N6=26-1=63 символа: (6)()()E ()()E F63 На 7-м шаге образуется N7= 27-1=127 символов. Нам нужно найти позиции от 117-й по 122-й. Проставим позиции, близкие к искомым: (7) ()()E()()EF()()E()()E125F126 G127 Получается,что элементы в позициях от 117-й по 122-й нужно смотреть в (): (4)AABAABCA117A118B119A120A121B122C123D124 Получили:AABAAB. Разбор задачи B8 (демо ЕГЭ 2009)Время выполнения-10 мин, уровень сложности-повышенный Строки (цепочки символов латинских букв) создаются по следующему правилу. Первая строка состоит из одного символа – латинской буквы «А». Каждая из последующих цепочек создается такими действиями: в очередную строку сначала записывается буква, чей порядковый номер в алфавите соответствует номеру строки (на i-м шаге пишется «i»-я буква алфавита), к ней справа дважды подряд приписывается предыдущая строка. Вот первые 4 строки, созданные по этому правилу: (1) A (2) BAA (3) CBAABAA (4) DCBAABAACBAABAA Латинский алфавит (для справки): ABCDEFGHIJKLMNOPQRSTUVWXYZ Запишите семь символов подряд, стоящие в восьмой строке со 126-го по 132-е место (считая слева направо). Ответ: BAAGFED Решение: Введем обозначение: "DCBAABAACBAABAA"-(). Распишем, какие будут созданы строки с 5-го по 8-й шаг. (5) E()() (6) F E()() E()() (7) G FE()()E()() FE()()E()() (8) H GFE()()E()()FE()()E()() GFE()()E()()FE()()E()() Чтобы определить позиции символов, нужно определить сколько символов образуется на каждом шаге. Количество символов определяется по формуле: Ni=2i-1, где i-шаг. На 7-м шаге образуется N7=27-1=127 символов: (7) G FE()()E()() FE()()E()()127 На 8-м шаге образуется N8= 28-1=255 символов.Перед вторым символ "G" элемент находится в позиции:1+N7=128: (8) H1 GFE()()E()()FE()()E()()128 GFE()()E()()FE()()E()() Нам нужно найти позиции от 126-и до 132-х. Расставим позиции: (8) H1 GFE()()E()()FE()()E()()128 G129F130E131()()E()()FE()()E()(). Элементы в позициях 126, 127,128, 132 нужно смотреть в (): D132CBAABAACBAAB126A127A128. Получили:BAAGFED. |