Вариант №1
1) Основание АD трапеции АВСD лежит в плоскости  . Через точки В и С . Через точки В и С
проведены параллельные прямые, пересекающие плоскость  в точках Е и F соответственно. в точках Е и F соответственно.
а) Каково взаимное расположение прямых ЕF и АВ?
б) Чему равен угол между прямыми ЕF и АВ, если 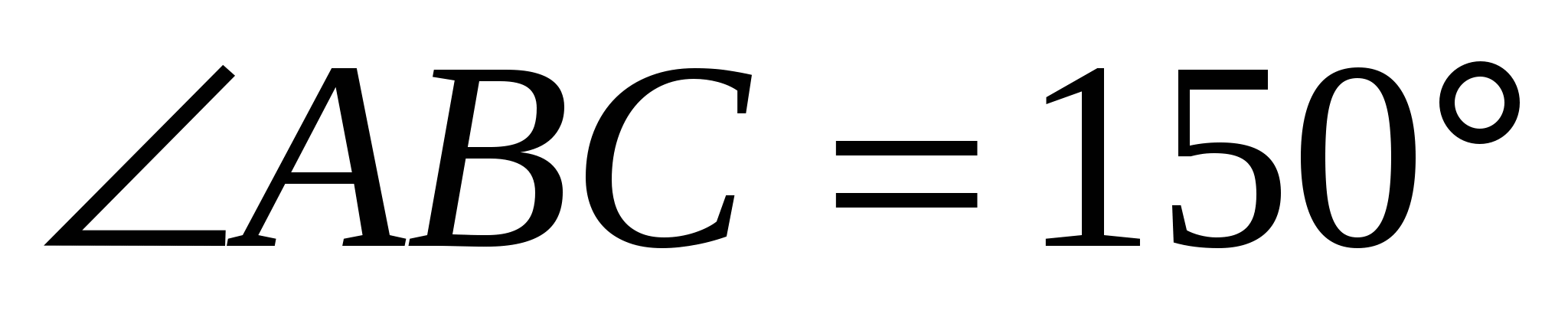 ? Ответ обоснуйте. ? Ответ обоснуйте.
2) Дан пространственный четырёхугольник АВСD, в котором диагонали АС и ВD равны. Середины сторон этого четырёхугольника соединены последовательно отрезками.
а) Выполните рисунок к задаче.
б) Докажите, что полученный четырёхугольник – ромб.
Вариант №2
1) Треугольники АВС и АDС лежат в разных плоскостях и имеют общую
сторону АС. Точка Р – середина стороны АD, точка К – середина DС.
а) Каково взаимное расположение прямых РК и АВ?
б) Чему равен угол между прямыми РК и АВ, если 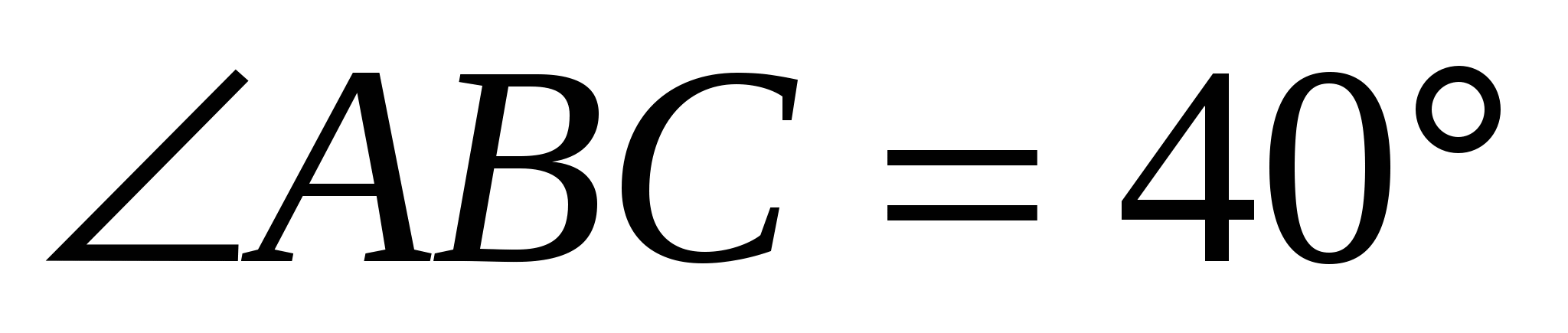 и и 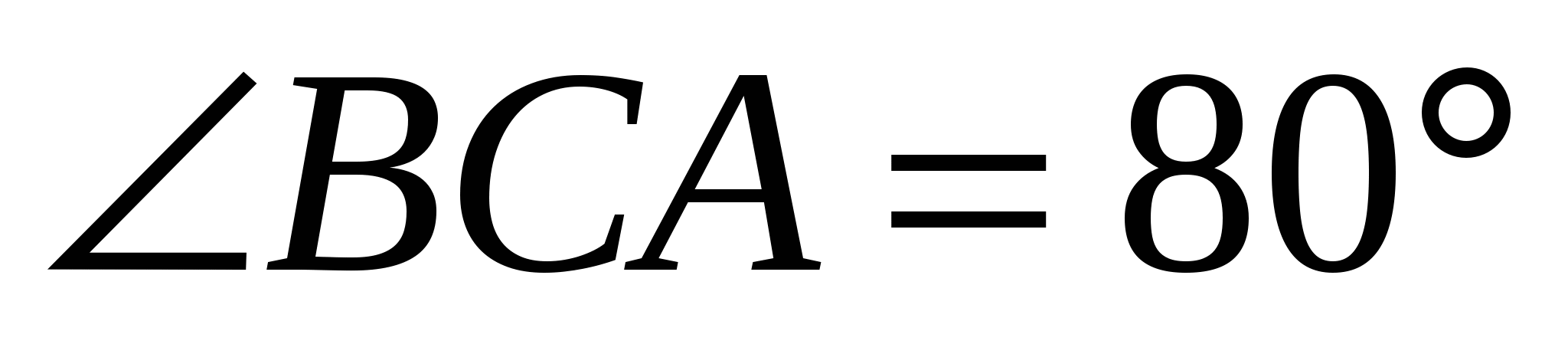 ? Ответ обоснуйте. ? Ответ обоснуйте.
2) Дан пространственный четырёхугольник АВСD, М и N середины сторон АВ и ВС соответственно, 
а) Выполните рисунок к задаче.
б) Докажите, что полученный четырёхугольник МNЕК – трапеция.
КОНТРОЛЬНАЯ РАБОТА № 2 «Параллельность прямых и плоскостей»
Вариант №1
1) Прямые a и b лежат в параллельных плоскостях  и и 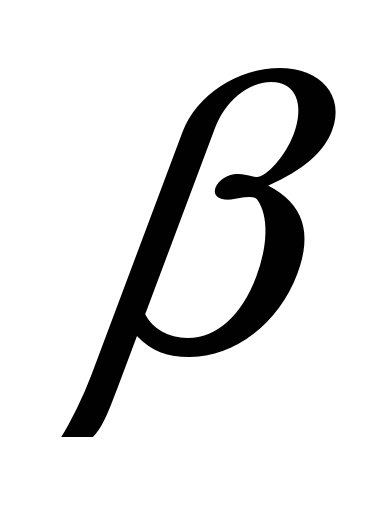 . Могут ли эти прямые быть параллельными; скрещивающимися? Сделайте рисунок для каждого возможного случая. . Могут ли эти прямые быть параллельными; скрещивающимися? Сделайте рисунок для каждого возможного случая.
2) Через точку О, лежащую между параллельными плоскостями  и и 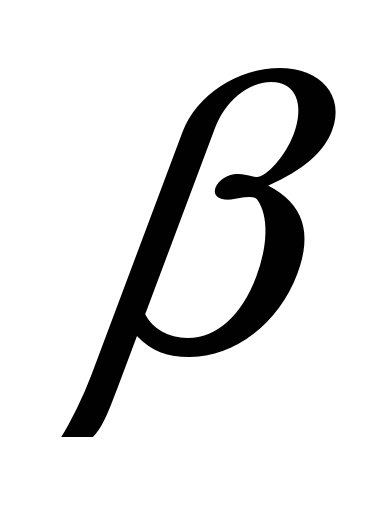 , проведены прямые l и m. Прямая l пересекает плоскости , проведены прямые l и m. Прямая l пересекает плоскости  и и 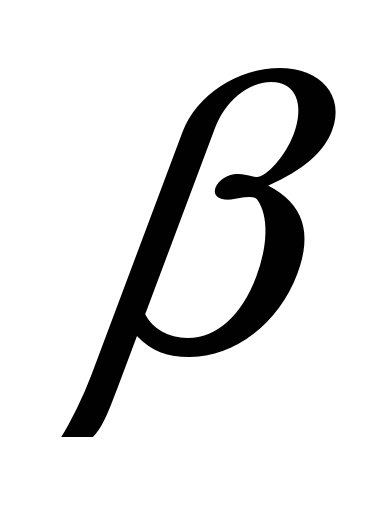 в точках A1 и A2 соответственно, прямая m – в точках В1 и В2. Найдите длину отрезка A2В2, если в точках A1 и A2 соответственно, прямая m – в точках В1 и В2. Найдите длину отрезка A2В2, если 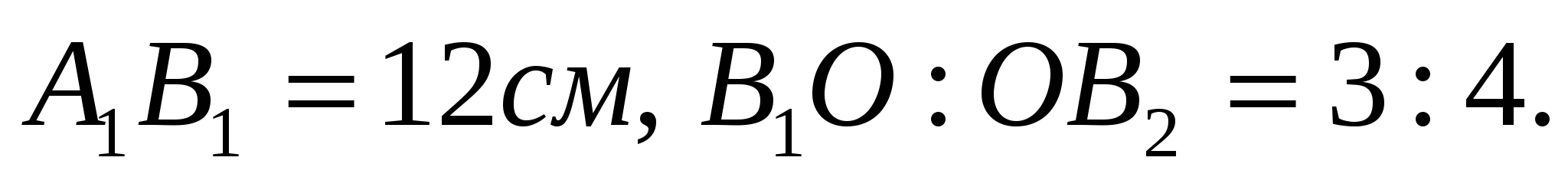
3) Дан параллелепипед АВСDA1B1C1D1. Постройте сечение параллелепипеда плоскостью, проходящей через точки М, N и К, являющиеся серединами рёбер АВ, ВС и DD1.
Вариант №2
1) Прямые a и b лежат в пересекающихся плоскостях  и и 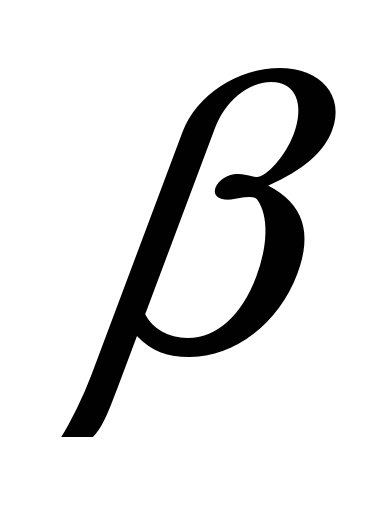 . Могут ли эти прямые быть параллельными; скрещивающимися? Сделайте рисунок для каждого возможного случая. . Могут ли эти прямые быть параллельными; скрещивающимися? Сделайте рисунок для каждого возможного случая.
2) Через точку О, не лежащую между параллельными плоскостями  и и 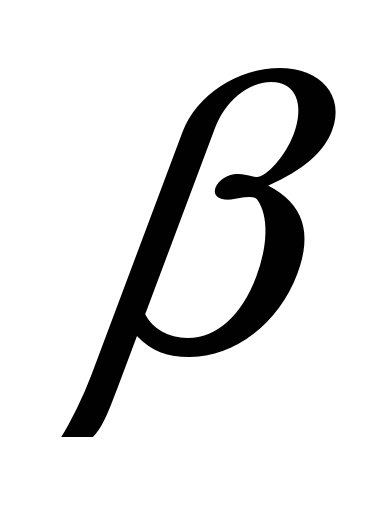 , проведены прямые l и m. Прямая l пересекает плоскости , проведены прямые l и m. Прямая l пересекает плоскости  и и 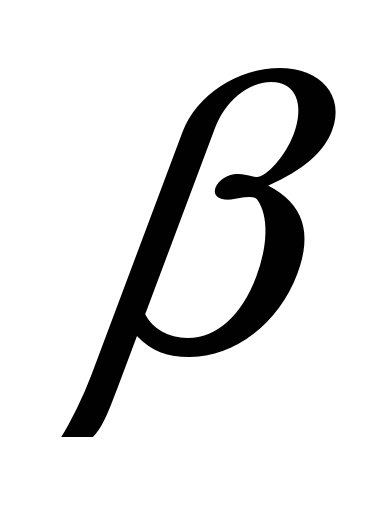 в точках A1 и A2 соответственно, прямая m – в точках В1 и В2. Найдите длину отрезка A1В1, если в точках A1 и A2 соответственно, прямая m – в точках В1 и В2. Найдите длину отрезка A1В1, если 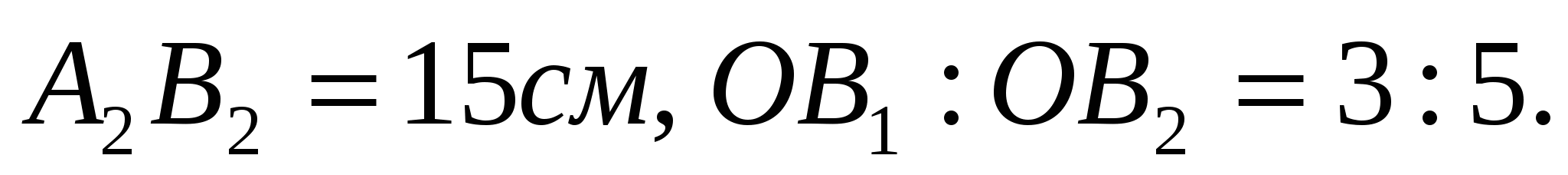
3) Дан тетраэдр DABC. Постройте сечение тетраэдра плоскостью, проходящей через точки М и N, являющиеся серединами рёбер DС и ВС, и точку К, такую, что 
КОНТРОЛЬНАЯ РАБОТА № 3 «Перпендикулярность прямых и плоскостей»
Вариант №1.
1) Диагональ куба равна 6см. Найдите:
а) Ребро куба.
б) Косинус угла между диагональю куба и плоскостью одной из его граней.
2) Сторона АВ ромба АВСD равна р, а один из углов ромба равен  . Через . Через
сторону АВ проведена плоскость  на расстоянии р/2 от точки D. на расстоянии р/2 от точки D.
а) Найдите расстояние от точки С до плоскости  . .
б) Покажите на рисунке линейный угол двугранного угла DАВМ, 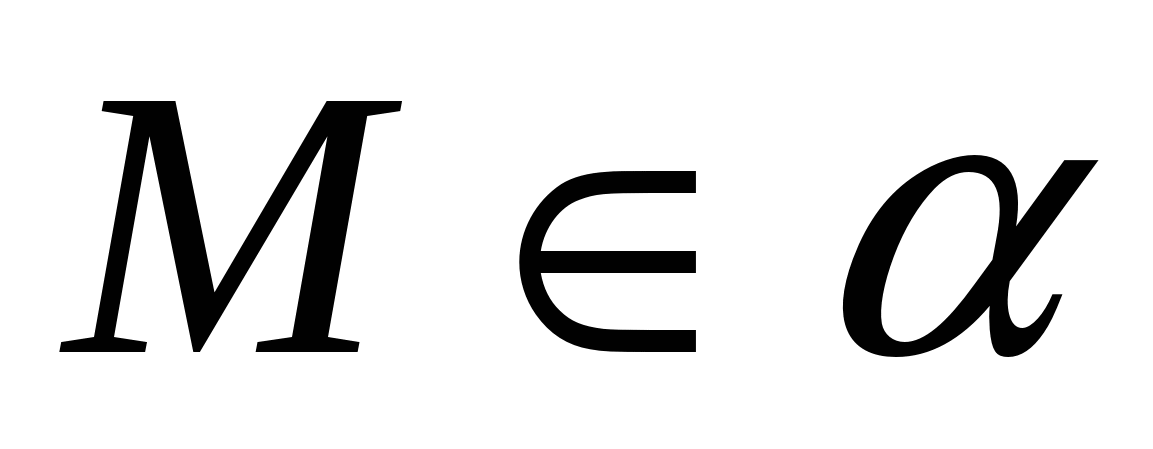 . .
в) Найдите синус угла между плоскостью ромба и плоскостью  . .
Вариант №2.
1) Основанием прямоугольного параллелепипеда служит квадрат, диагональ параллелепипеда равна 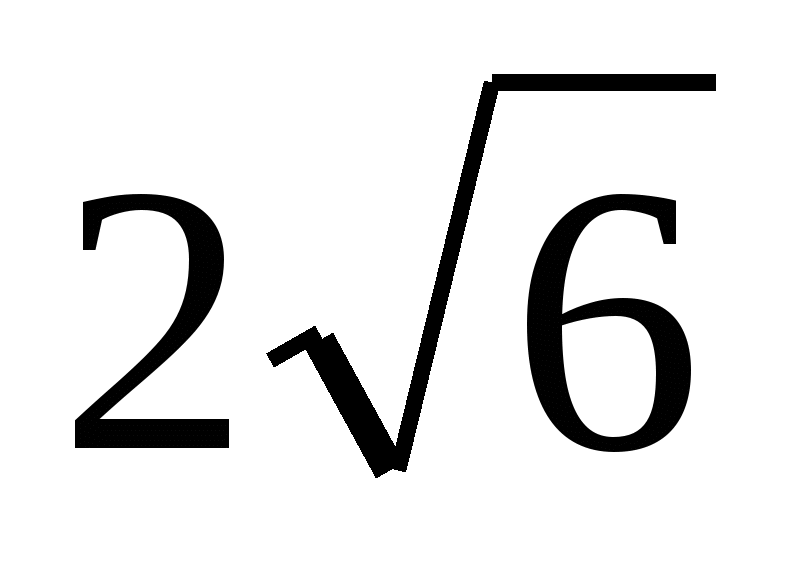 , а его измерения относятся как 1:1:2. Найдите: , а его измерения относятся как 1:1:2. Найдите:
а) Измерения параллелепипеда.
б) Синус угла между диагональю параллелепипеда и плоскостью его основания.
2) Сторона квадрата АВСD равна р. Через сторону АD проведена плоскость
 на расстоянии р/2 от точки В. на расстоянии р/2 от точки В.
а) Найдите расстояние от точки С до плоскости  . .
б) Покажите на рисунке линейный угол двугранного угла ВАDМ, 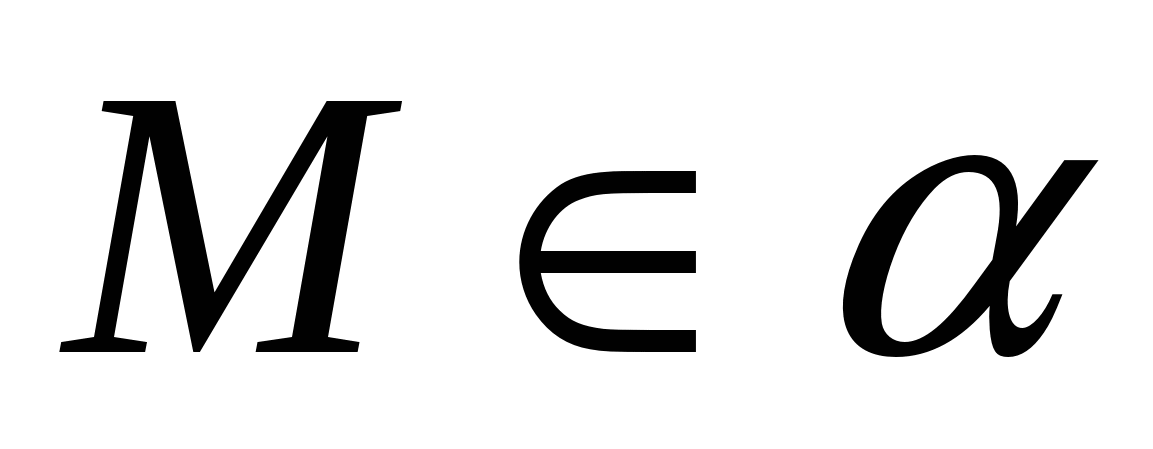 . .
в) Найдите угол между плоскостью квадрата и плоскостью  . .
КОНТРОЛЬНАЯ РАБОТА № 4 «Многогранники»
Вариант №1.
1) Основанием пирамиды DАВС является правильный треугольник АВС, сторона которого равна р. Ребро DА перпендикулярно к плоскости АВС, а плоскость DВС составляет с плоскостью АВС угол  . Найдите площадь боковой и площадь полной поверхности пирамиды. . Найдите площадь боковой и площадь полной поверхности пирамиды.
2) Основанием прямого параллелепипеда АВСDА1В1С1D1 является ромб АВСD сторона которого равна р и угол равен  . Плоскость АD1С1 составляет с плоскостью основания угол . Плоскость АD1С1 составляет с плоскостью основания угол  . Найдите: . Найдите:
а) Высоту ромба.
б) Высоту параллелепипеда.
в) Площадь боковой поверхности параллелепипеда.
г) Площадь поверхности параллелепипеда.
Вариант №2.
1) Основанием пирамиды МАВСD является квадрат АВСD. Ребро МD перпендикулярно к плоскости основания, АD = DМ = р. Найдите площадь боковой и площадь полной поверхности пирамиды.
2) Основанием прямого параллелепипеда АВСDА1В1С1D1 является параллелограмм АВСD, стороны которого равна р и 2р, острый угол равен и 2р, острый угол равен 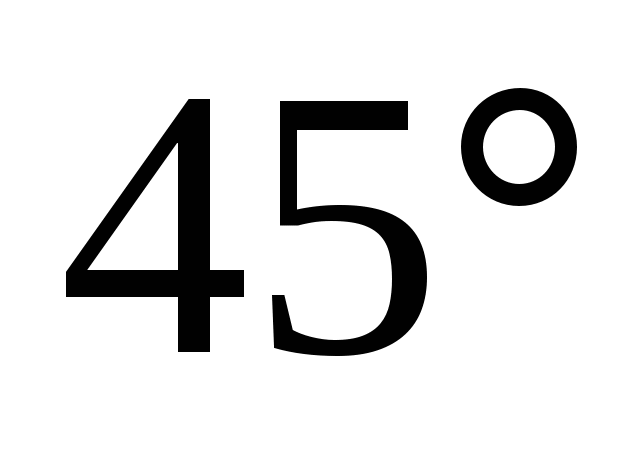 . Высота параллелепипеда равна меньшей высоте параллелограмма. Найдите: . Высота параллелепипеда равна меньшей высоте параллелограмма. Найдите:
а) Меньшую высоту параллелограмма.
б) Угол между плоскостью АВС1 и плоскостью основания.
в) Площадь боковой поверхности параллелепипеда.
г) Площадь поверхности параллелепипеда
Оценка устных ответов учащихся по математике
Ответ оценивается отметкой «5», если ученик:
полно раскрыл содержание материала в объеме, предусмотренном программой и учебником,
изложил материал грамотным языком в определенной логической последовательности, точно используя математическую терминологию и символику;
правильно выполнил рисунки, чертежи, графики, сопутствующие ответу;
показал умение иллюстрировать теоретические положения конкретными примерами, применять их в новой ситуации при выполнении практического задания;
продемонстрировал усвоение ранее изученных сопутствующих вопросов, сформированность и устойчивость используемых при отработке умений и навыков;
отвечал самостоятельно без наводящих вопросов учителя. Возможны одна - две неточности при освещении второстепенных вопросов или в выкладках, которые ученик легко исправил по замечанию учителя.
Ответ оценивается отметкой «4», если он удовлетворяет в основном требованиям на оценку «5», но при этом имеет один из недостатков:
допущены один – два недочета при освещении основного содержания ответа, исправленные по замечанию учителя;
допущены ошибка или более двух недочетов при освещении второстепенных вопросов или в выкладках, легко исправленные по замечанию учителя.
Отметка «3» ставится в следующих случаях:
неполно или непоследовательно раскрыто содержание материала, но показано общее понимание вопроса и продемонстрированы умения, достаточные для дальнейшего усвоения программного материала (определенные «Требованиями к математической подготовке учащихся»);
имелись затруднения или допущены ошибки в определении понятий, использовании математической терминологии, чертежах, выкладках, исправленные после нескольких наводящих вопросов учителя;
ученик не справился с применением теории в новой ситуации при выполнении практического задания, но выполнил задания обязательного уровня сложности по данной теме;
при знании теоретического материала выявлена недостаточная сформированность основных умений и навыков.
Отметка «2» ставится в следующих случаях:
не раскрыто основное содержание учебного материала;
обнаружено незнание или непонимание учеником большей или наиболее важной части учебного материала;
допущены ошибки в определении понятий, при использовании математической терминологии, в рисунках, чертежах или графиках, в выкладках, которые не исправлены после нескольких наводящих вопросов учителя.
Отметка «1» ставится, если:
ученик обнаружил полное незнание и непонимание изучаемого учебного материала или не смог ответить ни на один из поставленных вопросов по изучаемому материалу.
Оценка письменных контрольных работ учащихся по математике
Отметка «5» ставится, если:
работа выполнена полностью;
в логических рассуждениях и обосновании решения нет пробелов и ошибок;
в решении нет математических ошибок (возможна одна неточность, описка, не являющаяся следствием незнания или непонимания учебного материала).
Отметка «4» ставится, если:
работа выполнена полностью, но обоснования шагов решения недостаточны (если умение обосновывать рассуждения не являлось специальным объектом проверки);
допущена одна ошибка или два-три недочета в выкладках, рисунках, чертежах или графиках (если эти виды работы не являлись специальным объектом проверки).
Отметка «3» ставится, если:
допущены более одной ошибки или более двух-трех недочетов в выкладках, чертежах или графиках, но учащийся владеет обязательными умениями по проверяемой теме.
Отметка «2» ставится, если:
допущены существенные ошибки, показавшие, что учащийся не владеет обязательными умениями по данной теме в полной мере.
Отметка «1» ставится, если:
работа показала полное отсутствие у учащегося обязательных знаний и умений по проверяемой теме или значительная часть работы выполнена не самостоятельно.
Общая классификация ошибок
Грубыми считаются ошибки:
незнание определения основных понятий, законов, правил, основных положений теории, незнание формул, общепринятых символов обозначений величин, единиц их измерения;
незнание наименований единиц измерения;
неумение выделить в ответе главное;
неумение применять знания, алгоритмы для решения задач;
неумение делать выводы и обобщения;
неумение читать и строить графики;
потеря корня или сохранение постороннего корня;
отбрасывание без объяснений одного из них;
равнозначные им ошибки;
вычислительные ошибки, если они не являются опиской;
логические ошибки.
К негрубым ошибкам следует отнести:
неточность формулировок, определений, понятий, теорий, вызванная неполнотой охвата основных признаков определяемого понятия или заменой одного - двух из этих признаков второстепенными;
неточность графика;
нерациональный метод решения задачи или недостаточно продуманный план ответа (нарушение логики, подмена отдельных основных вопросов второстепенными);
нерациональные методы работы со справочной и другой литературой;
неумение решать задачи, выполнять задания в общем виде.
Недочетами являются:
нерациональные приемы вычислений и преобразований;
небрежное выполнение записей, чертежей, схем, графиков.
Материально-техническое обеспечение учебного предмета геометрии в 10 классе
ИНФОРМАЦИОННО-КОММУНИКАЦИОННЫЕ СРЕДСТВА
Мультимедийные обучающие программы и учебники
Справочные материалы по искусству и МХК
Электронная библиотека.
ТЕХНИЧЕСКИЕ СРЕДСТВА ОБУЧЕНИЯ (ТСО)
Мультимедийный компьютер
Технические требования: графическая операционная система, привод для чтения-записи компакт дисков, аудио-видео входы/выходы, возможность выхода в Интернет. Оснащен акустическими колонками, микрофоном и наушниками. С пакетом прикладных программ (текстовых, табличных, графических, презентационных, художественных и музыкальных)
Аудиторная доска с магнитной поверхностью и набором приспособлений для крепления таблиц, репродукций
Видеомагнитофон
Экран ( навесной)
Мультимедийный проектор
Сканер
Копировальный аппарат
Ссылки из Интернета
Единая коллекция - https://collection.cross-edu.ru/catalog/rubr/f544b3b7-f1f4-5b76-f453-552f31d9b164
Российский общеобразовательный портал - https://mat.edu.ru/
Детские электронные книги и презентации - https://viki.rdf.ru/
Список научно-методического обеспечения.
Атанасян Л. С. Геометрия. Учебник для 10-11 классов общеобразовательных учреждений. М., «Просвещение», 2006.
Дорофеев Г. В. и др. Оценка качества подготовки выпускников средней (полной) школы по математике. М., «Дрофа», 2002.
Концепция модернизации российского образования на период до 2010// «Вестник образования» -2002- № 6 - с.11-40.
Концепция математического образования (проект)//Математика в школе.- 2000. – № 2. – с.13-18.
Кузнецова Г.М., Миндюк Н.Г. Программы для общеобразовательных школ, гимназий, лицеев. Математика 5 – 11 классы. М., «Дрофа», 2003.
Федеральный компонент государственного стандарта среднего (полного) общего образования по математике //«Вестник образования» -2004 - № 14 - с.107-119.
Зив. Б.Г., Мейлер В.М., Баханский А.Г. Задачи по геометрии для 7-11 классов. М., 1991;
Кукарцева Г.И. Сборник задач по геометрии в рисунках и тестах, 10-11 класс. М.1999;
Звавич Л.И. Контрольные и проверочные работы по геометрии 10-11 класс. М., 2001;
Лысенко Ф.Ф. Математика ЕГЭ – 2008 . Вступительные экзамены
М. Рабинович «Геометрия 10-11. Задачи и упражнения на готовых чертежах», М.; Илекса. 2008.
Дорофеев Г.В., Муравин Г.К., Седова Е.А. Сборник заданий для подготовки и проведения письменного экзамена по математике (курс А) и алгебре и началам анализа (курс В) за курс средней школы. 11 кл. М.,Дрофа, 2004.
Энциклопедия для детей. Т. 11, Математика, М., 1999
CD – диски. Виртуальная школа Кирилла и Мифодия. Уроки геометрии.
CD- диски. Математика7-11. TeachPro.
|
 Скачать 0.57 Mb.
Скачать 0.57 Mb.