«Графический способ решения систем уравнений»

Скачать 49.45 Kb. Название «Графический способ решения систем уравнений» Дата 12.02.2016 Размер 49.45 Kb. Тип Самостоятельная работа

Урок по алгебре в 7 классе Тема: «Графический способ решения систем уравнений». Цели: Научить решать системы линейных уравнений с двумя переменными графическим способом. Развитие исследовательских способностей учащихся, самоконтроля, речи. Воспитание культуры общения, аккуратности. Методы: Диалог Проверка по готовым ответам Исследование Формы: Фронтальный опрос Самостоятельная работа Работа в парах Работа с презентацией и интерактивными средствами. Ход урока: Сообщение темы урока, постановка целей урока. (в тетради записать число, тему) Устный счет. Является ли решением системы уравнений х+7=у пара чисел (0;0); (2;-2); (8;1); (0;3); (6;0),(-4,3). 3х+4у=0 Является ли линейным уравнение с двумя переменными: 5ху+3=0; у-х=13; 3у-х2=1; х2-х(х+5)+4у=3. Выразите переменную у через х из уравнения х+у=1; 3х-у=2. Решите уравнение х=6; 2,5х=0; 0х=5; 0х=0. При каком значении k график линейной функции у=kх-6: Параллелен графику у=3х+1? Пересекает график функции у=3х+1? Совпадает с графиком функции у=-2х-6?. Логическая задача «Определить профессию». В отделении банка работают кассир, контролер и заведующий. Их фамилии Борисов, Иванов и Сидоров. Кассир не имеет ни братьев, ни сестер и меньше всех ростом. Сидоров женат на сестре Борисова и ростом выше контролёра. Назовите фамилии контролера и заведующего. Борисов Иванов Сидоров Кассир - + - Контролёр + - - Заведующий - - + Ответ: Актуализация знаний. Работа по понятиям. Определение линейного уравнения с двумя переменными. Что называется решением линейного уравнения с двумя переменными? Что называется графиком линейного уравнения с двумя переменными? Что является графиком линейного уравнения с двумя переменными? Сколько точек определяет прямую? Что значит решить систему уравнений? Что называется решением системы линейных уравнений с двумя переменными? Когда две прямые на плоскости пересекаются? Когда две прямые на плоскости параллельны? Когда две прямые на плоскости совпадают? Изучение нового материала. Как вы понимаете выражение «графический способ решения систем уравнений?» Вы уже умеете строить график линейного уравнения, это самое главное умение, которое нужно для решения систем уравнений графическим способом. Для того, чтобы научиться решать системы уравнений графическим способом, вам нужен алгоритм решения. Алгоритм у вас на партах. Следуя четким указаниям алгоритма, вы сами научитесь решать системы уравнений графическим способом, это первая ваша задача на уроке и вторая задача - выяснить, исследовать, сколько решений может иметь система линейных уравнений? (Разбить на три группы Алёна и Паша и Юля, Настя и Чечин С. ,Щукин С. и Коля, ). Каждой группе задания на листочках. 1 группе. Решить систему уравнений графическим способом, используя алгоритм. 2х+у=8 2х-у=0 Как расположены прямые на плоскости? Сколько общих точек? Сколько решений имеет система уравнений? Сделайте общий вывод. (Ответ: 1 решение, (2,4)) 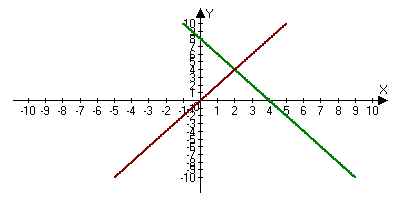2 группе. Решить систему уравнений графическим способом, используя алгоритм. 3х+у=2 -6х-2у=-4 Как расположены прямые на плоскости? Сколько общих точек? Сколько решений имеет система уравнений? Сделайте общий вывод. (Ответ: прямые совпали, множество решений). 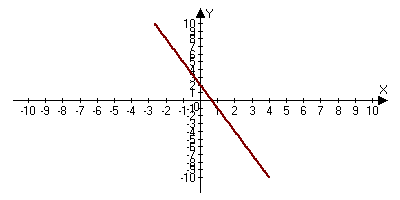3 группе. Решить систему уравнений графическим способом, используя алгоритм. 2х-3у=4 4х-6у=-2 Как расположены прямые на плоскости? Сколько общих точек? Сколько решений имеет система уравнений? Сделайте общий вывод. (Ответ: прямые параллельны, нет решений). 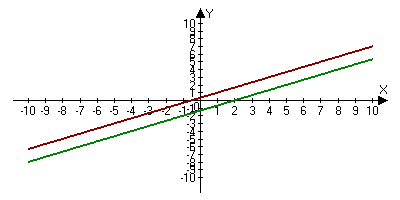Физминутка для глаз (презентация). После выполнения работы, каждой группе предоставить слово для формулировки выводов. Сделать общий вывод :(схема, раздаю каждому ребенку) Если угловые коэффициенты прямых различны, то система имеет единственное решение. Если угловые коэффициенты прямых одинаковы, то система не имеет решений. Если угловые коэффициенты прямых и коэффициент b одинаковы, то система имеет бесконечно много решений. (Закрепление решить у доски №1124 (б)) Вводный контроль. Самостоятельно решить систему уравнений графическим способом. (интерактивное средство на двух сторонах, сразу проверить). х-у=1 3х+3у=9 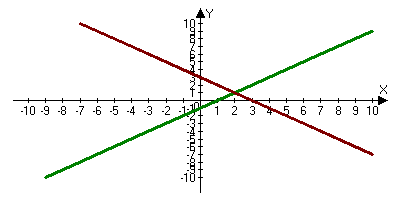Ответ: (2,1) Дополнительное задание задача на слайде (№721, ответ: 9 км.) х/12=х/18+15/60, х-расстояние АВ. х/12- х/18=1/4 (3х-2х)/36=1/4 Х=9 км. Задача на смеси ( карточка) Подвести итоги (оценки). Рефлексия. Повторим алгоритм решения систем лин. уравнений графическим способом. Сколько решений может иметь система уравнений? Кто научился решать системы линейных уравнений графическим способом? Кто не научился? Кто ещё сомневается? Поднимите руки, кому урок понравился? Кому нет? Кто равнодушен? (программа) IX. Домашнее задание: написать заранее на доске Всем п. 41, Коле и Паше №1124 (а),№1122, Остальным №1124(в, г),№1123 Алгоритм построения графика линейного уравнения с двумя переменными. Выразить переменную у через х. «Взять» две точки, определяющие прямую. Построить график уравнения (прямую). Алгоритм решения системы линейных уравнений с двумя переменными графическим способом. Построить графики каждого из уравнений системы. Найти координаты точки пересечения прямых. Записать ответ. Задача на смеси. Смешали 200 гр. 20% раствора кислоты и 300 гр. 40 % раствора кислоты. Определите массу кислоты и ее процентное содержание в полученном растворе. ( Ответ: 500гр., 32%.) решение:20% от 200гр.-0,2*200=40гр., 40%от 300 гр.- 0,4*300=120 гр. Кислоты. Раствор 500гр-100%,а кислоты 40+120=160 гр, 160-х%. х=16000:500=32%.