«Вычисление объемов тел с помощью определенного интеграла»
 Скачать 66.8 Kb.
|
Группа № 1 Объем наклонной призмы.  В папке – кейс содержатся следующие материалы
«Вычисление объемов тел с помощью определенного интеграла».
Задание № 1. Выведите формулу для нахождения объема наклонной призмы, используя метод интегрирования. Теорема. Объем пирамиды равен одной трети произведения площади основания на высоту. План доказательства:
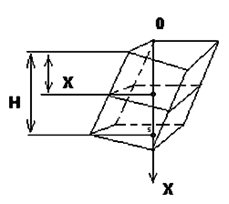
Существует другой способ нахождения объема наклонной призмы (через перпендикулярное сечение) . Задание № 2 Решите задачи
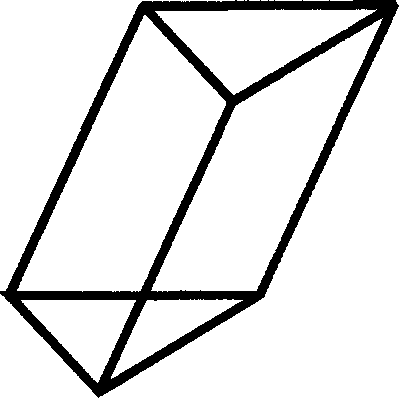
. Задание № 3 Защита вывода формулы объема наклонной призмы, решение стандартных задач. Распределить между членами группы выполнение заданий для компактного представления материала. Задание № 4. Придумайте или найдите задачи на нахождения объема призмы, задачи с использованием формулы объема призмы для учащихся других групп (Из различных источников). Найдите задачи, решите их самостоятельно, оформите их для представления учащимся других групп и затем будьте экспертами при решении ими задач (каждой группе по 2 задачи) Задание № 5 Задачи практического содержания
Нео куб был придуман в США в 2008 году, а популярность ему принесли видеоролики выложенные на You Tube. Неокуб считается отличным средством снятия стресса и развития мелкой моторики. Основа неокуба маленький магнитный шарик (классический магнит неодим-железо-бор) покрытый никелем для защиты от механических повреждений. Неодим практически не размагничивается, поэтому волноваться за потерю магнитных свойств не надо. Количество шариков - 216 шт. Диаметр шариков - 7 мм. Какой она имеет объем как наклонная призма?  
Испанские башни-близнецы Пуэрта-де-Эуропа пережили финансовый скандал, а теперь похоже бросают вызов закону всемирного тяготения нависая над Пасео-де-Кастельяна. Стены зданий наклонены под углом в 15 градусов от вертикали, их высота 115 метров, в основании площадки квадратной формы. Какой объем в пространстве они занимают? Интересное о призмах Термин “призма” греческого происхождения и буквально означает “отпиленное” (тело). История создания призмы. Еще в древности существовали два пути определения геометрических понятий. Первый вел от фигур высшего порядка к фигурам низшего. Такой точки зрения придерживался, в частности, Евклид, определяющий поверхность как границу тела, линию - как границу поверхности, концы же линии - как точки. Второй путь ведет, наоборот, от фигур низшего измерения к фигурам высшего: движением точки образуется линия, аналогично из линий составляется поверхность и т. д. Одним из первых, который соединил обе эти точки зрения, был Герон Александрийский, писавший, что тело ограничивается поверхностью и вместе с этим может быть рассмотрено как образованное движением поверхности. В появившихся позже на протяжении веков учебниках геометрии принималась за основу то одна, то другая, а иногда и обе вместе точки зрения. Подобно тому, как треугольник в понимании Евклида не являются пустым, т. е. представляет собой часть плоскости, ограниченную тремя неконкурентными (т. е. не пересекающимися в одной точке) отрезками, так и многогранник у него не пустой, не полый, а чем-то заполненный (по-нашему - частью пространства). В античной математике, однако, понятия отвлеченного пространства еще не было. Евклид определяет призму как телесную фигуру, заключенную между двумя равными и параллельными плоскостями (основаниями) и с боковыми гранями - параллелограммами. Для того чтобы это определение было вполне корректным, следовало бы, однако, доказать, что плоскости, проходящие через пары непараллельных сторон оснований, пересекаются по параллельным прямым. Евклид употребляет термин “плоскость” как в широком смысле (рассматривая ее неограниченно продолженной во все направления), так и в смысле конечной, ограниченной ее части, в ч  астности грани, аналогично применению им термина “прямая” (в широком смысле - бесконечная прямая и в узком - отрезок). В XVIII в. Тейлор дал такое определение призмы: это многогранник, у которого все грани, кроме двух, параллельны одной прямой. В памятниках вавилонской и древнеегипетской архитектуры встречаются такие геометрические фигуры, как куб, параллелепипед, призма. Важнейшей задачей египетской и вавилонской геометрии было определение объема различных пространственных фигур. Эта задача отвечала необходимости строить дома, дворцы, храмы и другие сооружения. Стереометрия возникла позже, чем планиметрия. Евклид дает следующее определение призмы: “Призма есть телесная (т.е. пространственная) фигура, заключенная между плоскостями, из которых две противоположные равны и параллельны, остальные же - параллелограммы”. Тут, как и во многих других местах, Евклид употребляет термин “плоскость” не в смысле безгранично продолженной плоскости, а в смысле ограниченной ее части, грани, подобно тому как “прямая” означает у него и отрезок прямой. Жемчужина Невьянска – наклонная башня высотой 57,5 м с отклонением от вертикали на 1,8 м. Наклон очень заметен – не только со стороны, но и при подъеме на башню: порой кажется, что она реально «заваливается» куда-то в бок и лестница уходит из под ног. Это, однако, только видимость и кажимость – на самом деле башня никуда не падает, и ее наклон уже давно не изменяется. С  уществует куча версий, почему башня наклонная. Авторам этих версий почему-то хочется думать, что ее строили такой специально (например, чтобы указывать направление на Тулу – родину Демидовых). Скорее всего, однако, она просто накренилась в процессе строительства. Основание башни буквально пронизано железными связями – у меня создалось впечатление, что только поэтому башня не рухнула, несмотря на сильный наклон. Демидов был очень предусмотрителен… |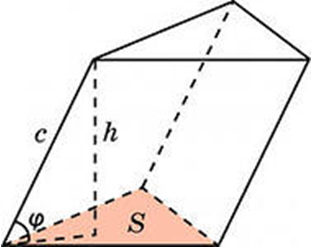
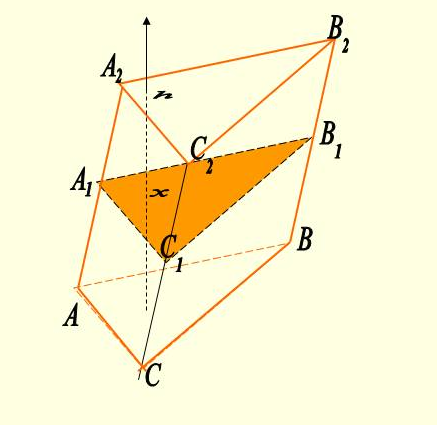начала докажите теорему для треугольной призмы.
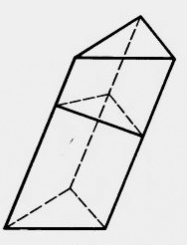наклонной призме боковое ребро равно 7 см, перпендикулярное сечение - прямоугольный треугольник с катетами: 4 см и 3 см. Найдите объем призмы.
адрид часто называют городом тысячи лиц, это название отражает разнообразие архитектурных стилей Мадрида. Здесь есть помпезные и богато украшенные здания, расположенные на границах Старого Мадрида вокруг Главной площади и Пласа-де-ла-Вилья. В эпоху Бурбонов архитекторы отошли от старых форм, создав новый стиль архитектуры барокко. В середине XVIII в. со вступлением на престол Карлоса III в моду вошел более строгий стиль – неоклассицизм. По мере того, как город рос и расширялся, росло и пристрастие мадридцев к новым архитектурным стилям. Сегодня архитекторы Мадрида продолжают экспериментировать с самыми смелыми строительными