|
Решение заданий, содержащих уравнения и неравенства с параметрами|
ИТОГОВОЕ ПОВТОРЕНИЕ СЕМИНАРЫ 7-8
Задание С5. Решение заданий, содержащих уравнения и неравенства с параметрами.
Необходимые навыки: вариативные действия в зависимости от значений параметра при алгебраическом решении уравнений и неравенств; навыки создания графических иллюстраций в осях хОу, анализ расположения однопараметрических семейств кривых (сдвиги и растяжения); навыки создания графических иллюстраций в осях переменная-параметр, навыки чтения графиков и определения количества и качества решений уравнения; работа с основными свойствами функций – монотонность, выпуклость, ограниченность, четность-нечетность; использование симметрий в множестве решений.
ОЧЕНЬ желательные навыки, помогающие облегчить решение: владение техникой перехода к равносильной системе или совокупности условий, в том числе в задачах с модулями; умение строить графики и анализировать уравнения и неравенства с модулями; владение понятием кусочно-заданной функции, в особенности составленной из квадратичных и линейных фрагментов; нахождение точек экстремума( в том числе без производной) или конструирование нужной комбинации отрезков квадратичных или линейных функций по заданным условиям на экстремумы; умение работать с квадратичной функцией, в том числе применять теоремы о расположении корней квадратного трехчлена.
Советы:
1) Построение графика в осях хОу удобно прочитывается в условии. Но требует аккуратности при перемещении линий, зависящих от параметра – сдвигах и вращениях. Работа в осях переменная – параметр дает стабильную картинку, но требует большей предварительной работы. Что выбрать – дело вкуса. Кроме того, в каждой конкретной задаче смотрите, какой способ графического решения (если оно вам симпатично) лучше выбрать, то есть под какой способ сделана задача.
2) Обращайте внимание на ВСЕ слова в условии. Это может помочь.
3) Пробуйте найти ВСЕ варианты взаимного расположения фигур. Может быть, Вы что-то не заметили… Все рассмотренные случаи могут дать некоторое количество баллов.
4) Вовремя сделанная замена переменной сильно облегчает решение.
5) Обращайте внимание на симметричность условия.
6) Умение работать со сложной функцией входит в необходимый набор знаний. Обращайте внимание на ограниченность множества значений функции.
7) Свойства входящих в условие функций могут помочь в неочевидных случаях.
8) Обычно задачи сводятся к рассмотрению хорошо известных функций и типов уравнений и неравенств. Поэтому повторите свойства линейной и квадратичной функций. И, конечно, поучитесь заранее работать с кусочно-заданными функциями.
Характеристика блоков заданий:
Блок 1 – Подготовка к выполнению задач уровня С3. Основные приемы в заданиях весьма умеренного уровня сложности.
Блок 2 – Работа на занятии. Задания немного более высокого уровня, или более комплексные, включающие различные приемы. Заданий достаточно много, преподаватель имеет возможность выбрать, какие примеры надо в первую очередь разобрать на семинарах. Всем, даже хорошо решающим, есть, чем заняться.
Блок 3 – Домашнее задание. Большая практика решения задач - большая вероятность успеха на экзамене!
Внимание! Задания не всегда расположены в порядке возрастания сложности!
Примеры для разбора на занятии:
Задание
|
Ответ
|
|
Блок 1. (обязательный минимум-подготовка к задачам ЕГЭ)
|
|
При каждом значении а решите неравенство 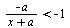 . .
|
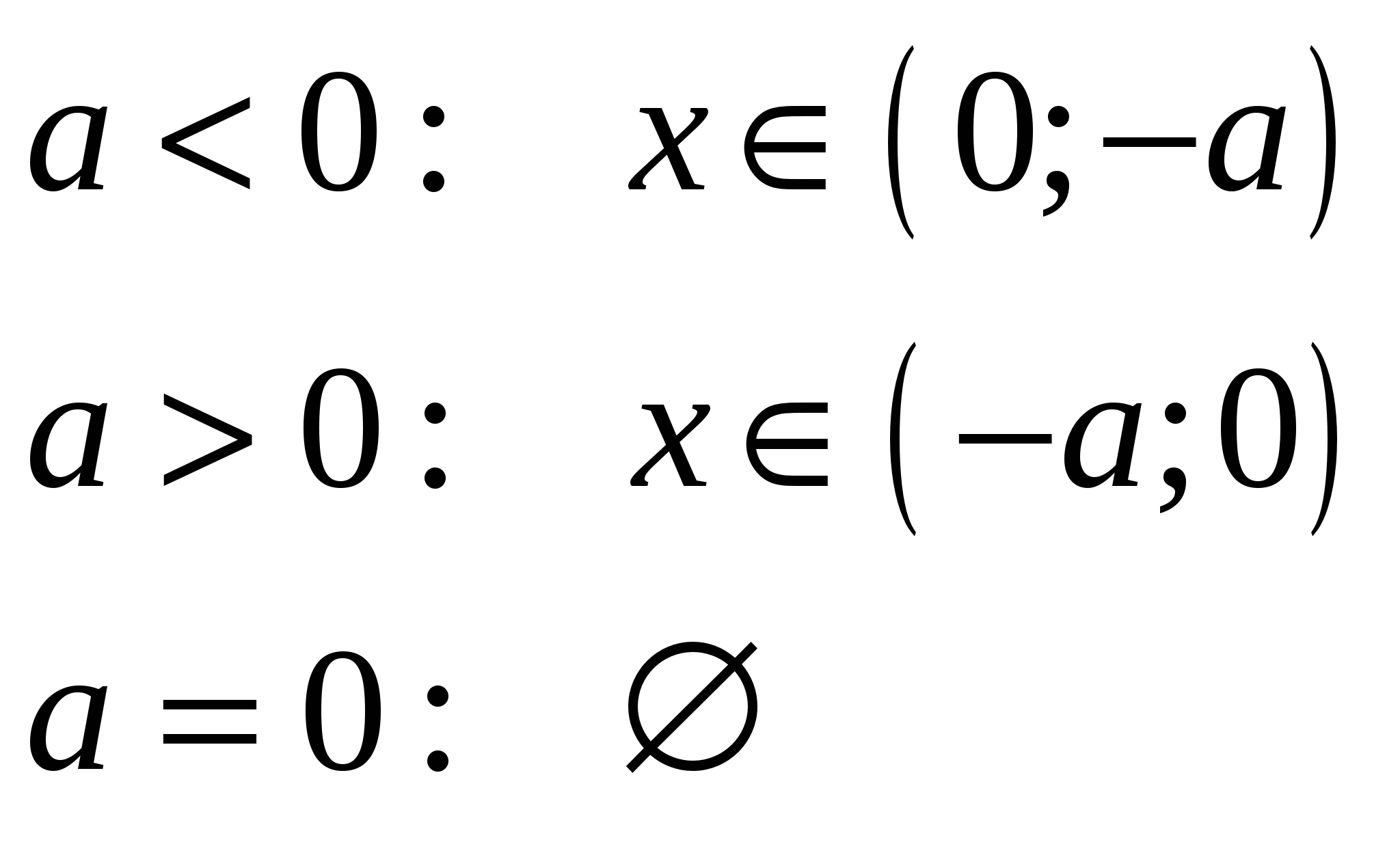
|
Найдите все значения параметра  , при каждом из которых график функции , при каждом из которых график функции 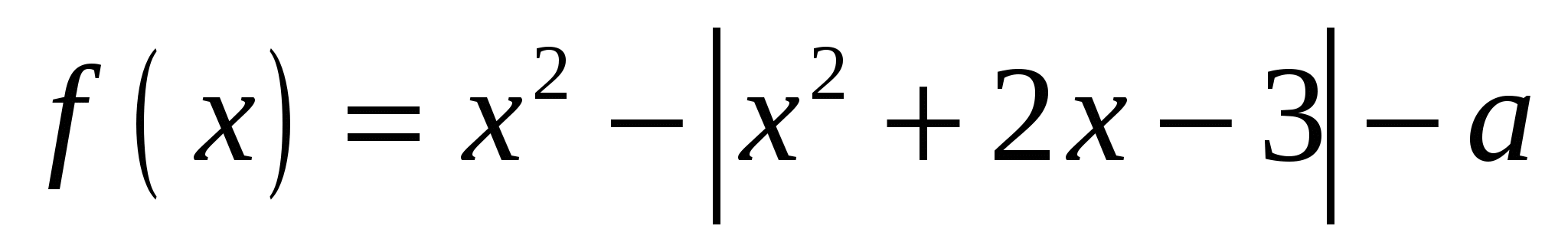 пересекает ось абсцисс более чем в двух различных точках. пересекает ось абсцисс более чем в двух различных точках.
|
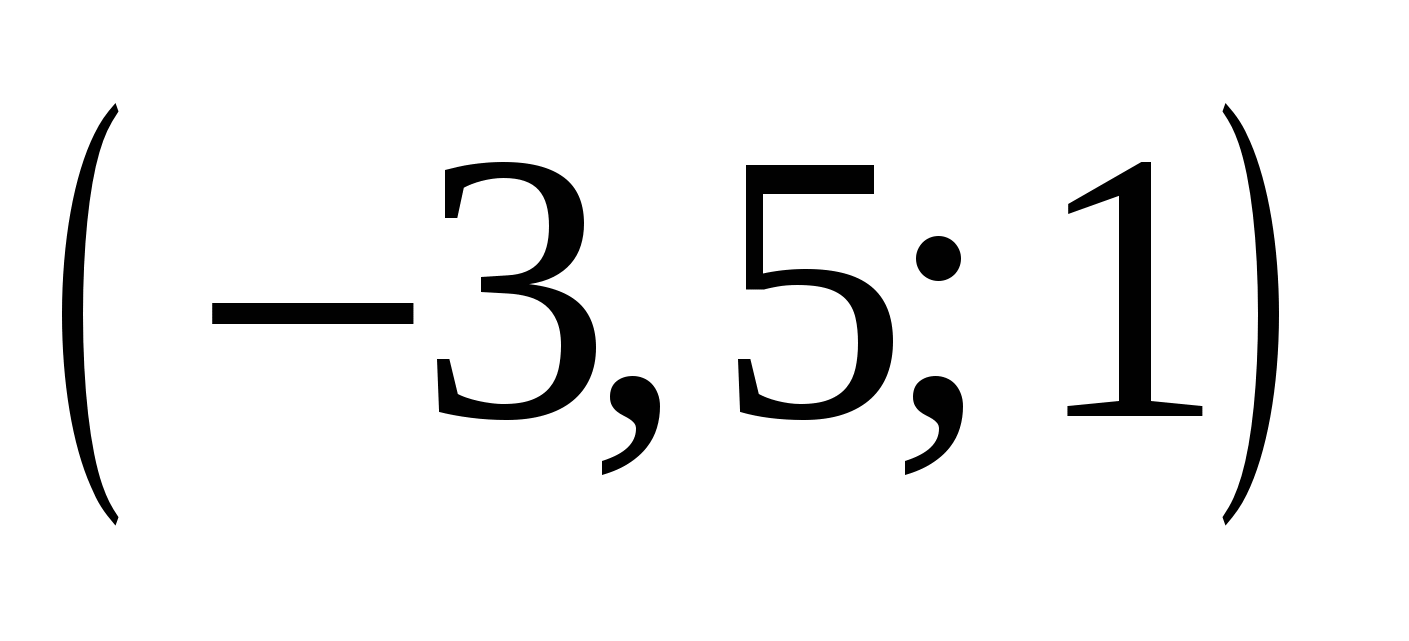
|
Найдите все значения параметра  , при каждом из которых неравенство , при каждом из которых неравенство 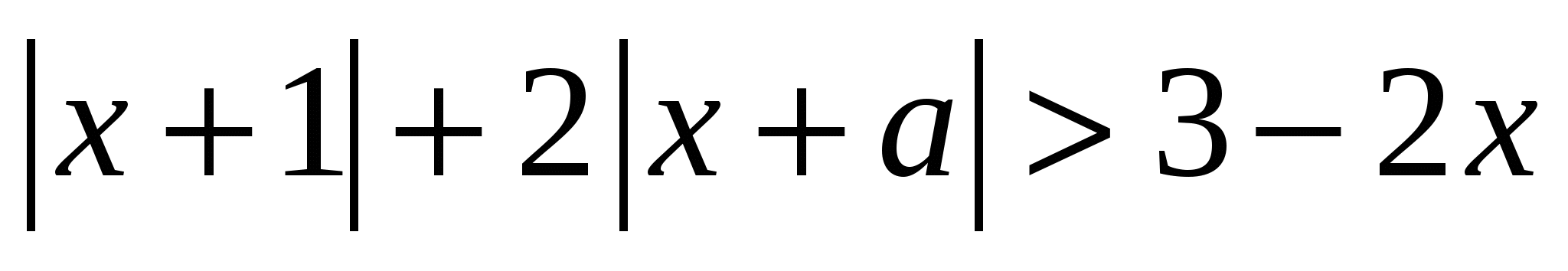 выполняется для любого выполняется для любого 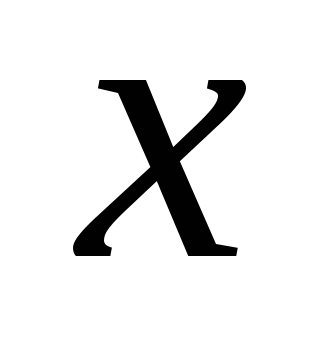 . .
|
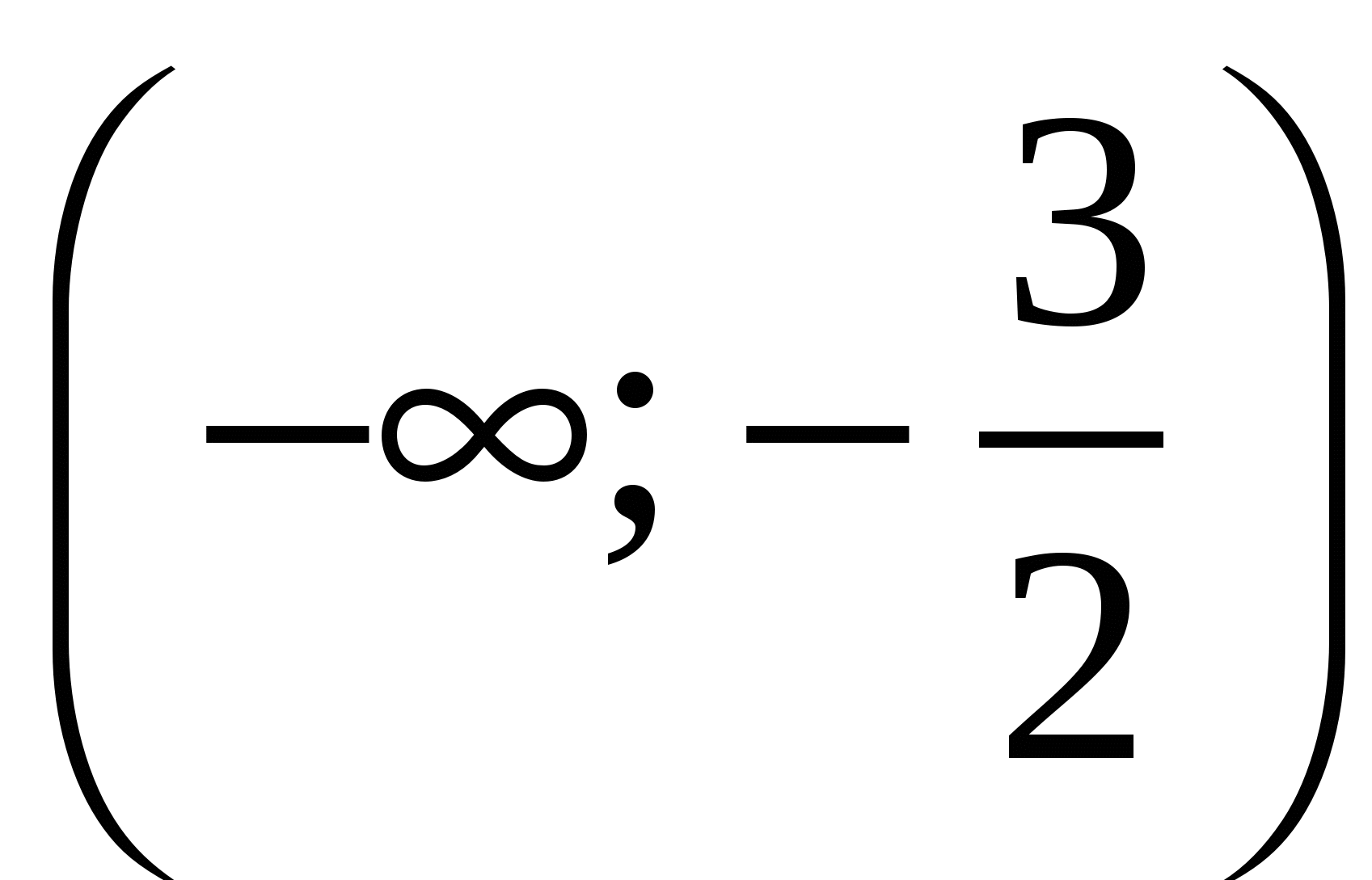
|
Найдите все значения параметра a, при которых система уравнений 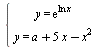 имеет два решения. имеет два решения.
|
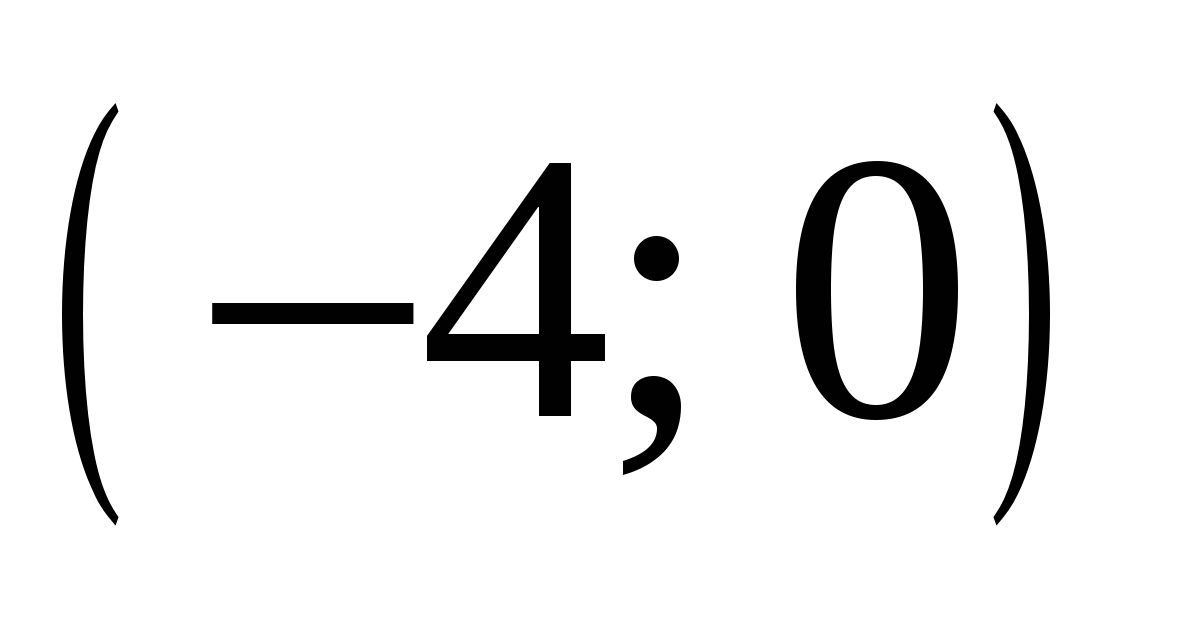
|
Найдите все значения параметра а, при каждом из которых система уравнений 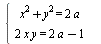 имеет ровно два решения. имеет ровно два решения.
|
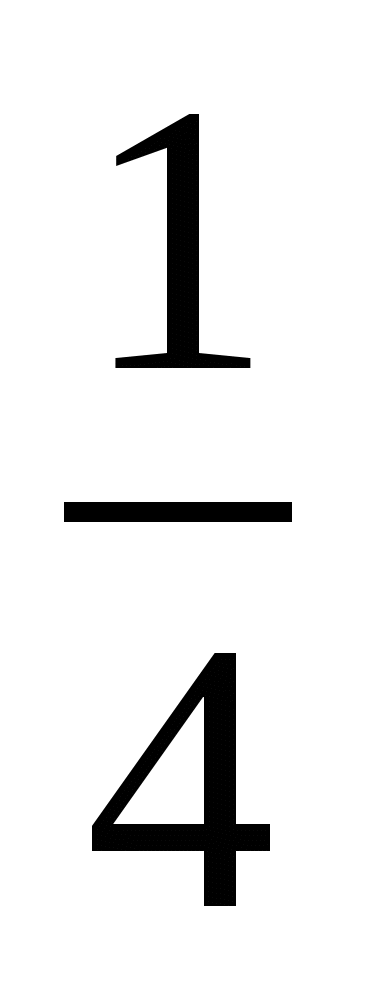
|
Блок 2. (задания уровня ЕГЭ)
|
Найдите все значения  , при каждом из которых уравнение , при каждом из которых уравнение 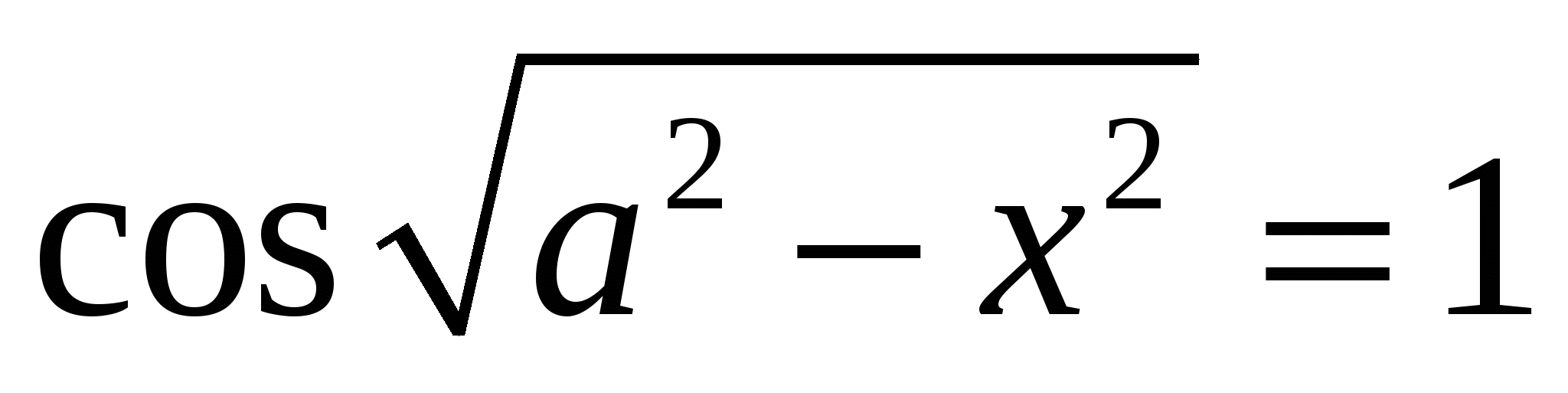 имеет ровно 8 решений. имеет ровно 8 решений.
|
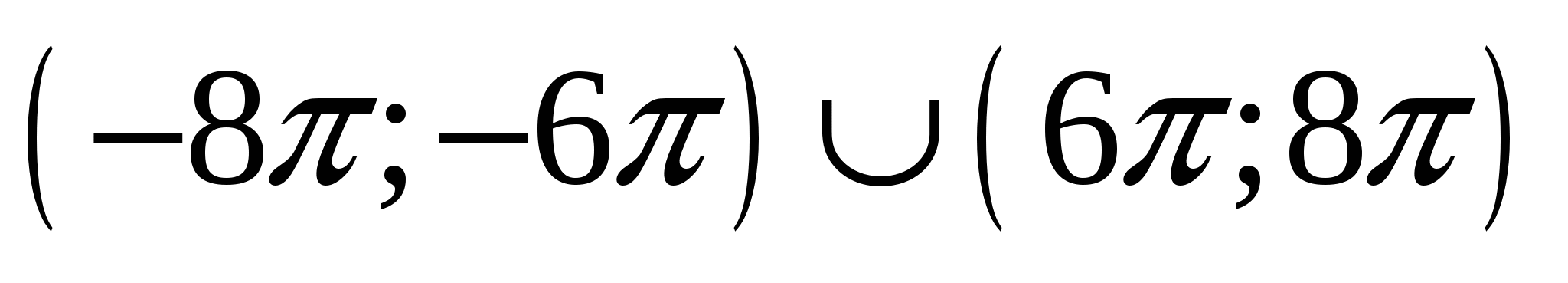
|
Найдите все значения параметра b , при каждом из которых корни уравнения 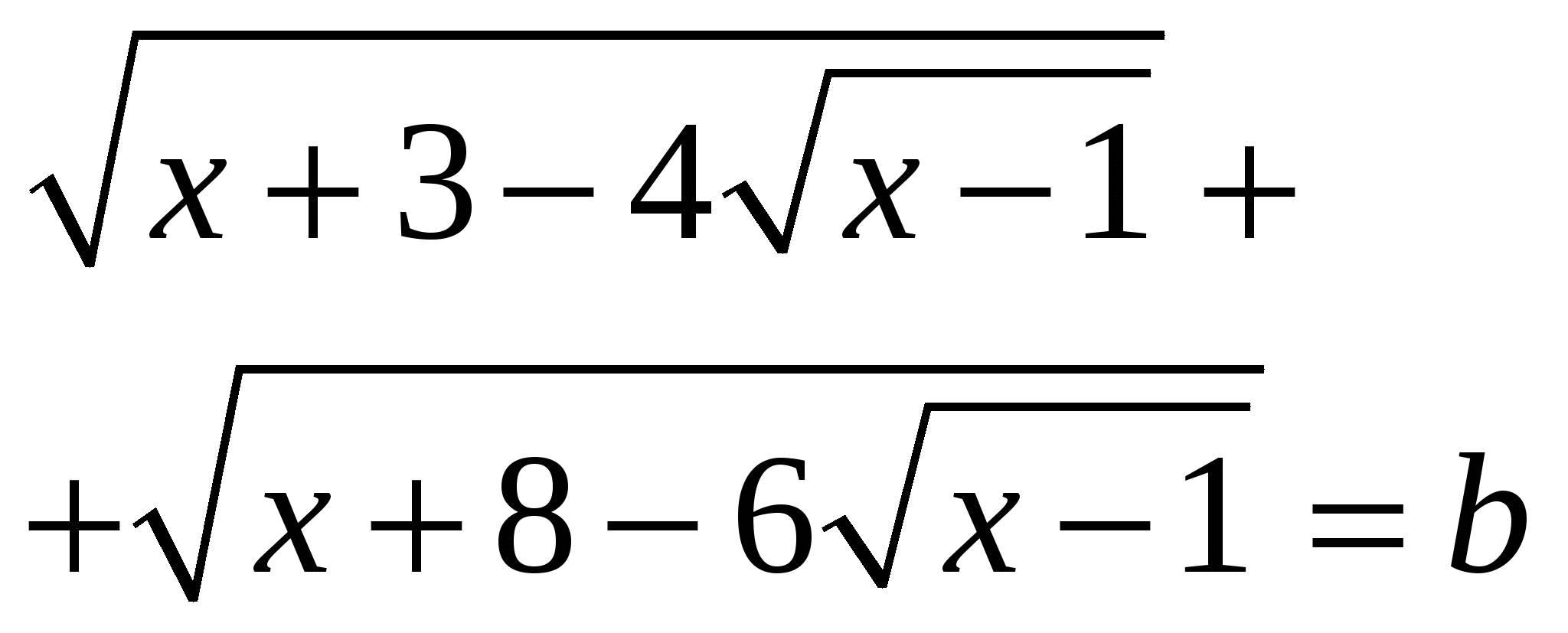 существуют и принадлежат отрезку |2;17]. существуют и принадлежат отрезку |2;17].
|
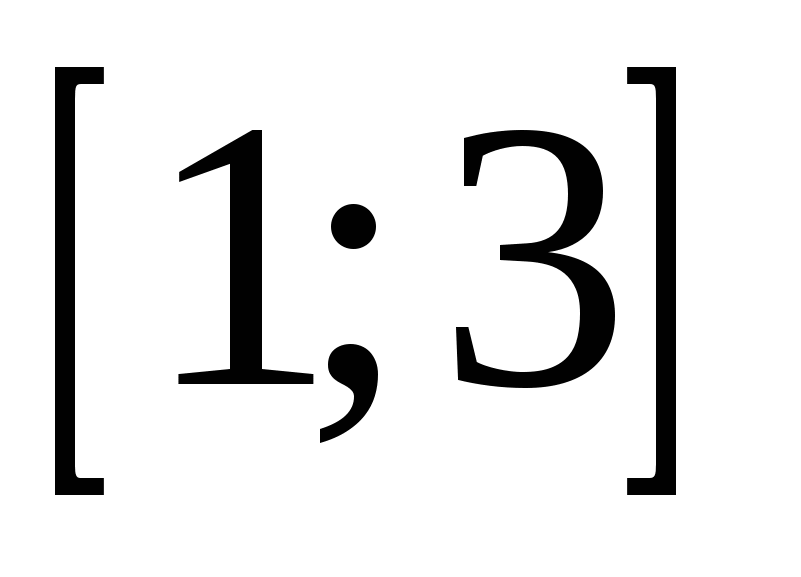
|
Найдите все значения а, при каждом из которых система 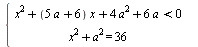 имеет решения. имеет решения.
|
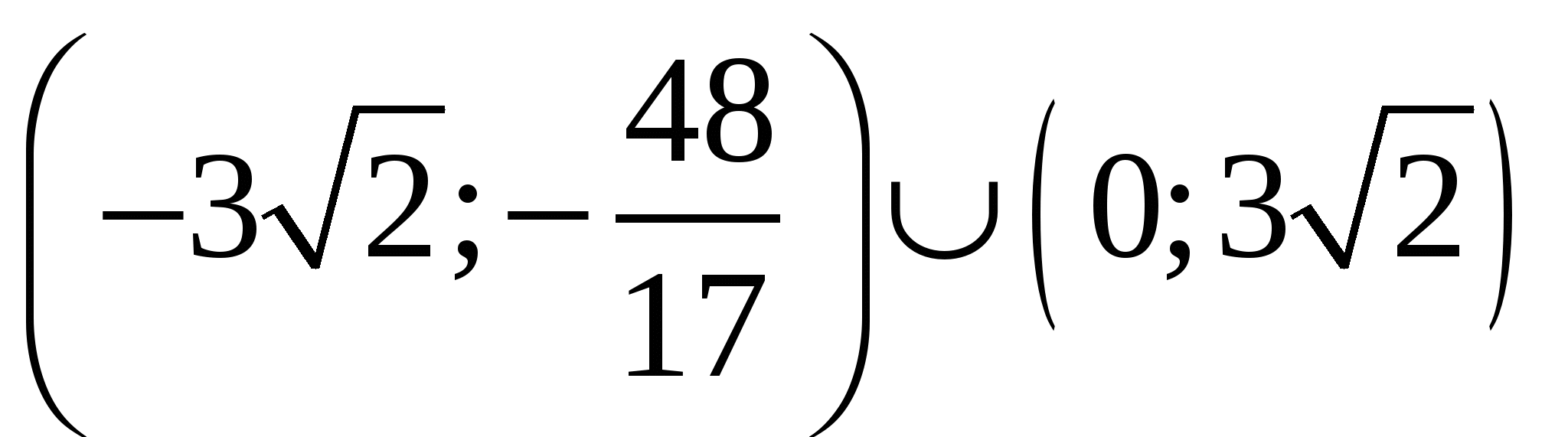
|
Найдите все значения а, при каждом из которых множество значений функции 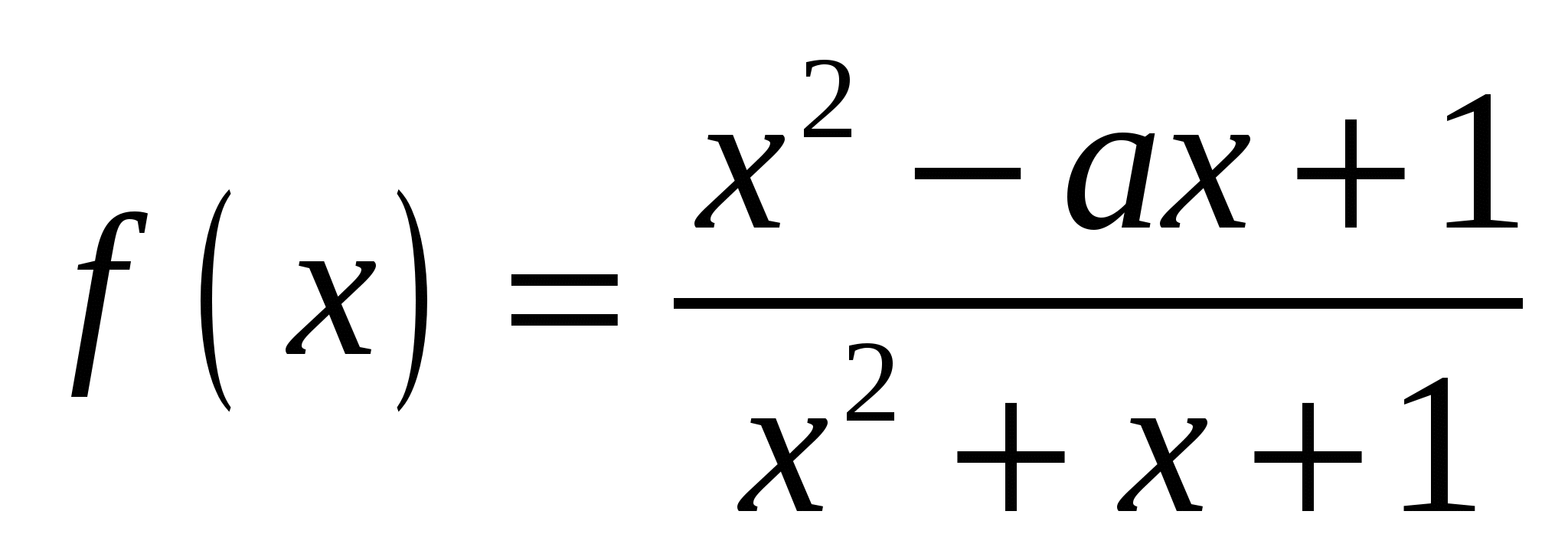 лежит в интервале лежит в интервале 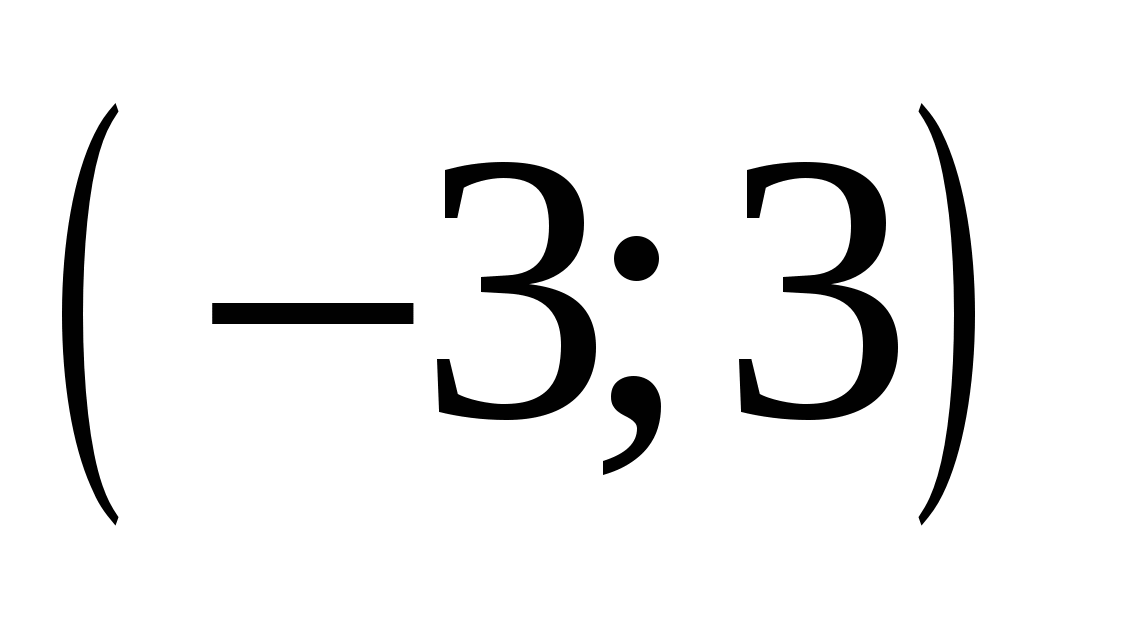 . .
|
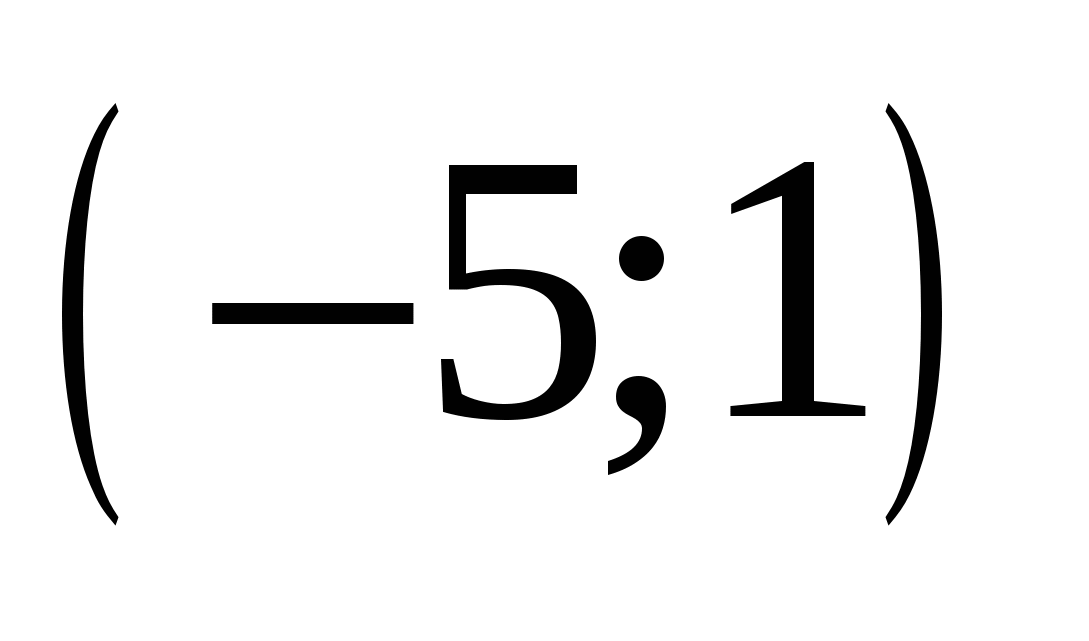
|
При каких значениях параметра С уравнение 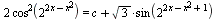 имеет решения ? имеет решения ?
|
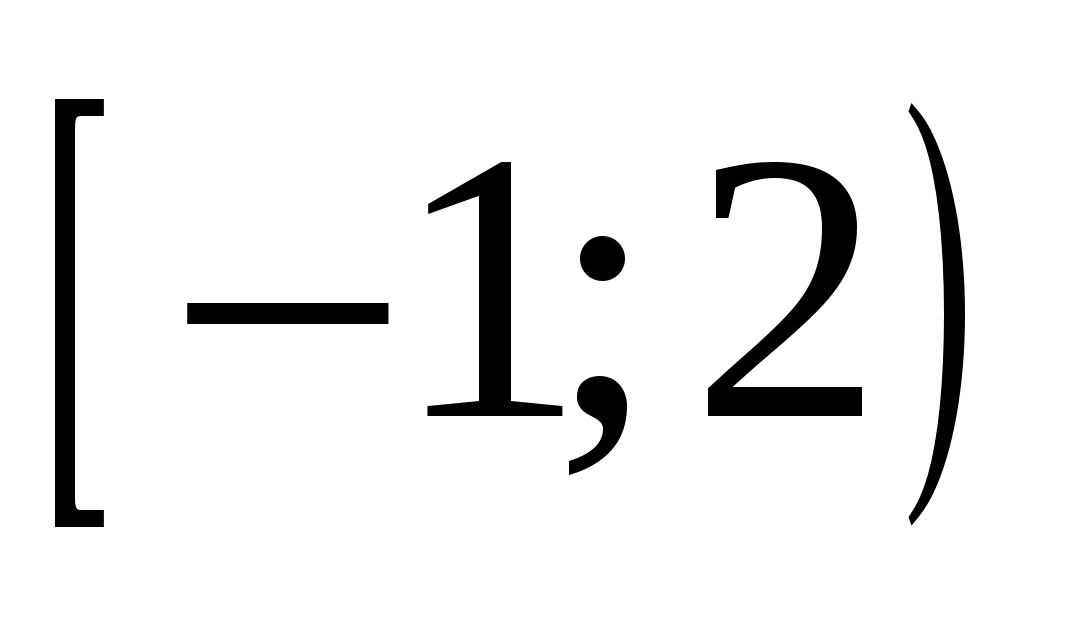
|
Найдите все значения а, при которых система 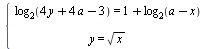 имеет решения. имеет решения.
|
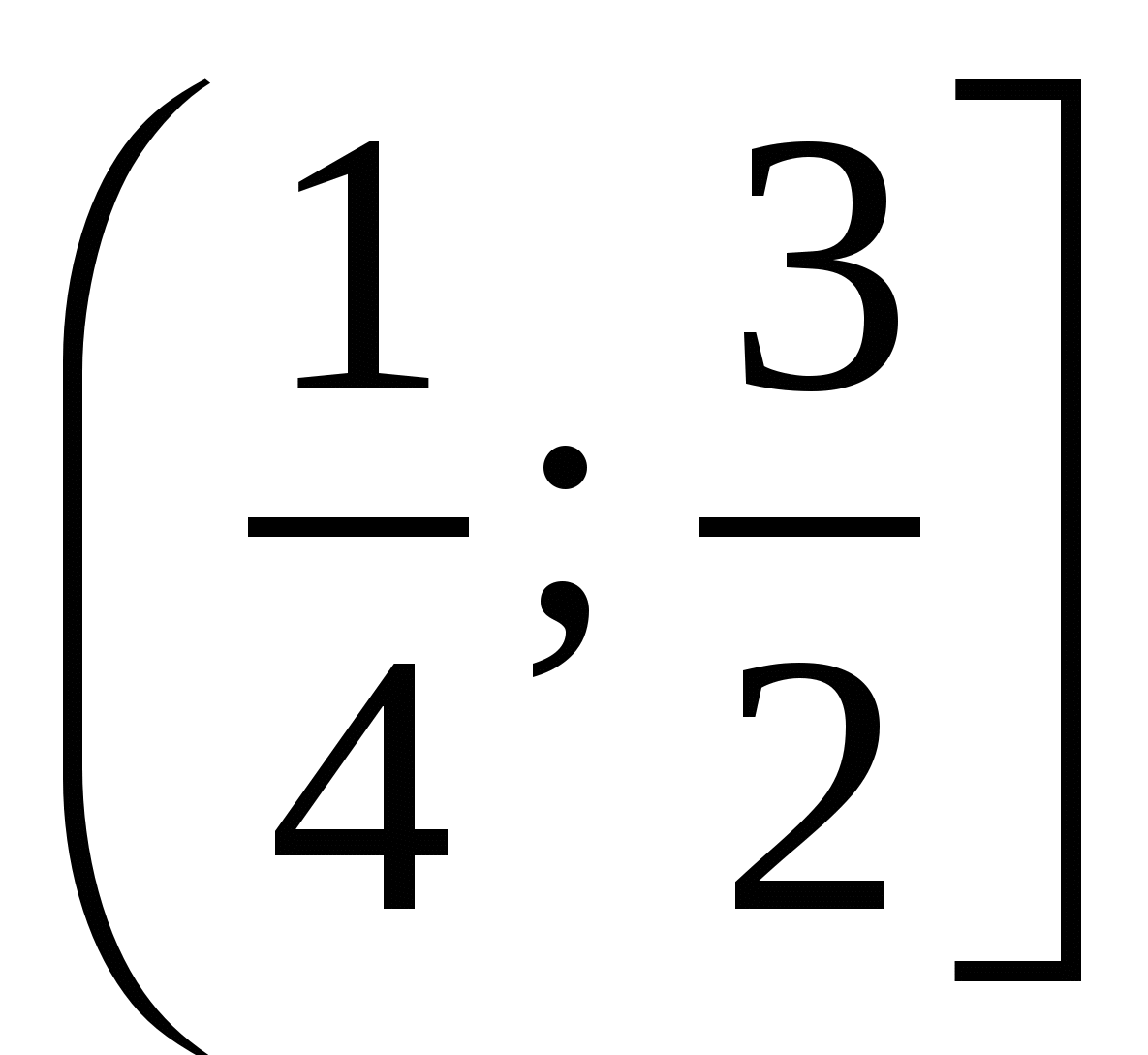
|
Найдите все положительные значения а, при каждом из которых система 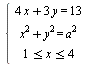 имеет единственное решение. имеет единственное решение.
|
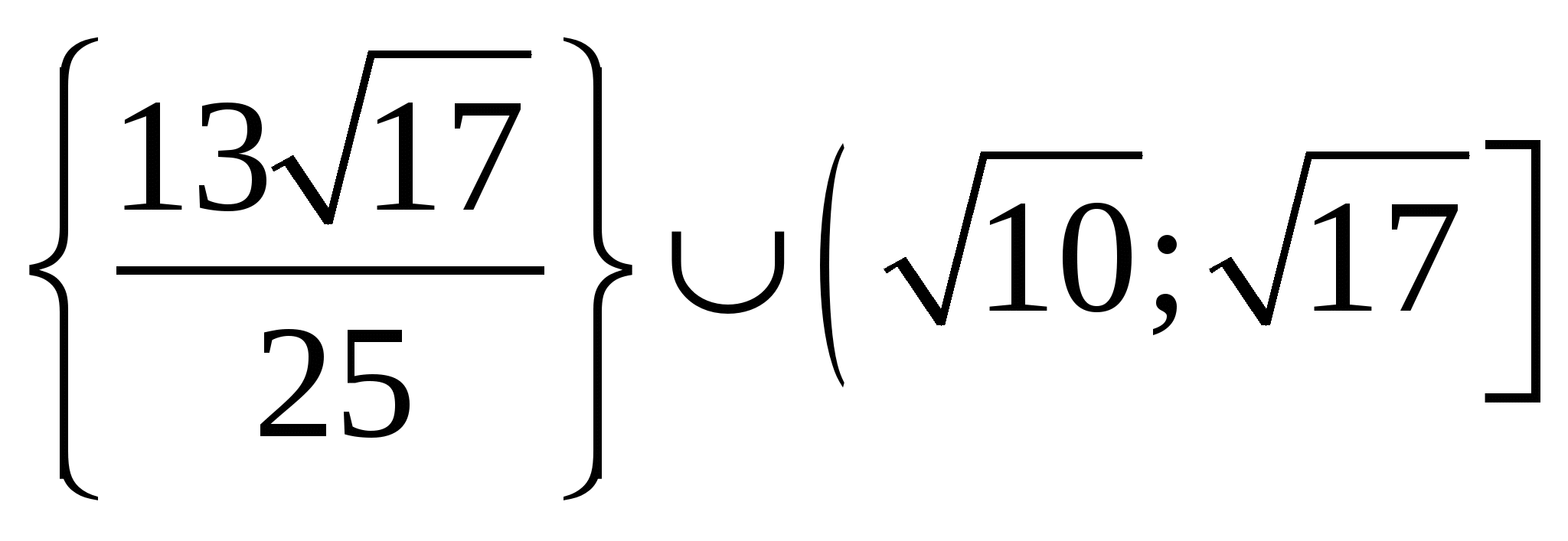
|
Найдите все значения а и b такие, что система 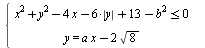 имеет ровно 2 различных решения. имеет ровно 2 различных решения.
|
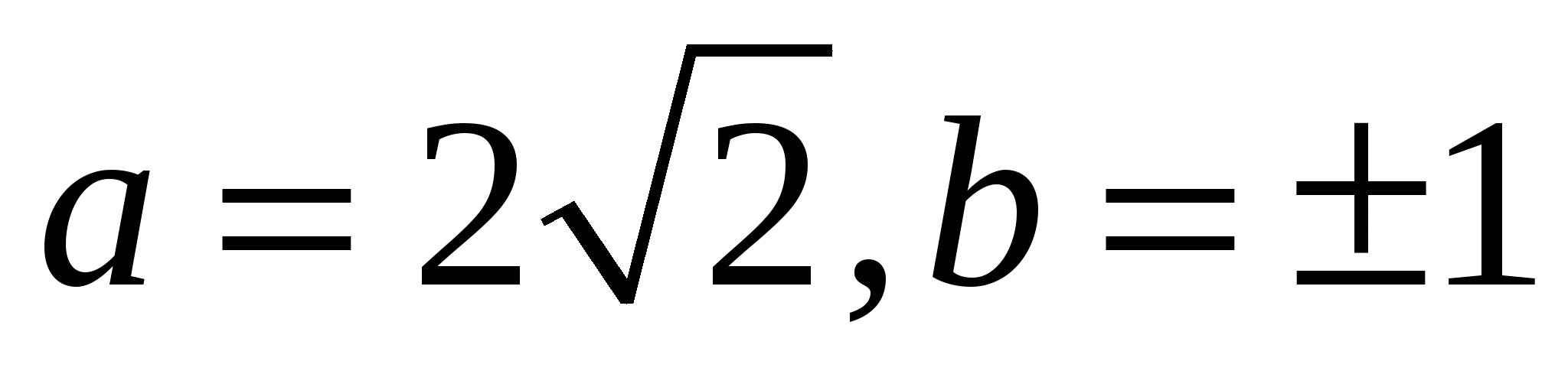
|
Найдите все значения a, при каждом из которых функция 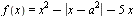 имеет более двух точек экстремума. имеет более двух точек экстремума.
|
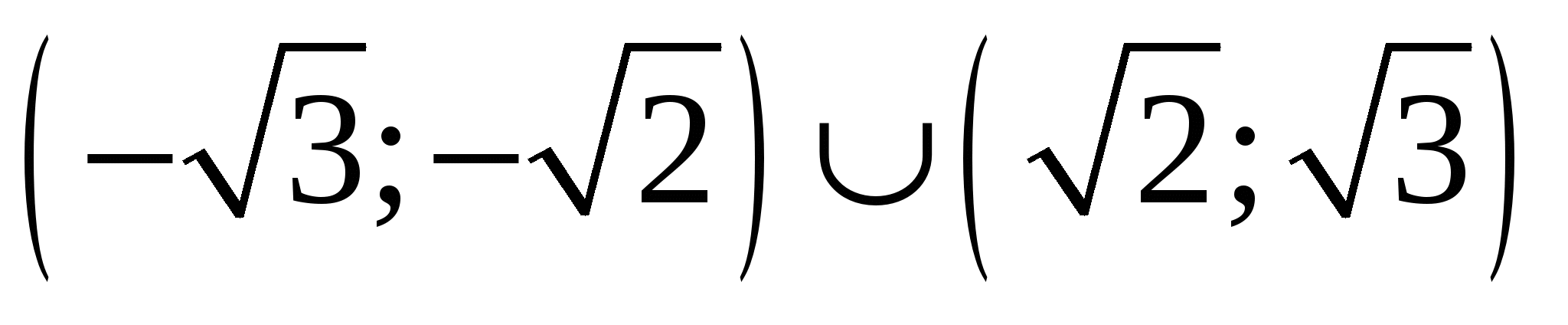
|
Найдите все значения a, при каждом из которых наименьшее значение функции 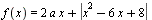 меньше 1. меньше 1.
|
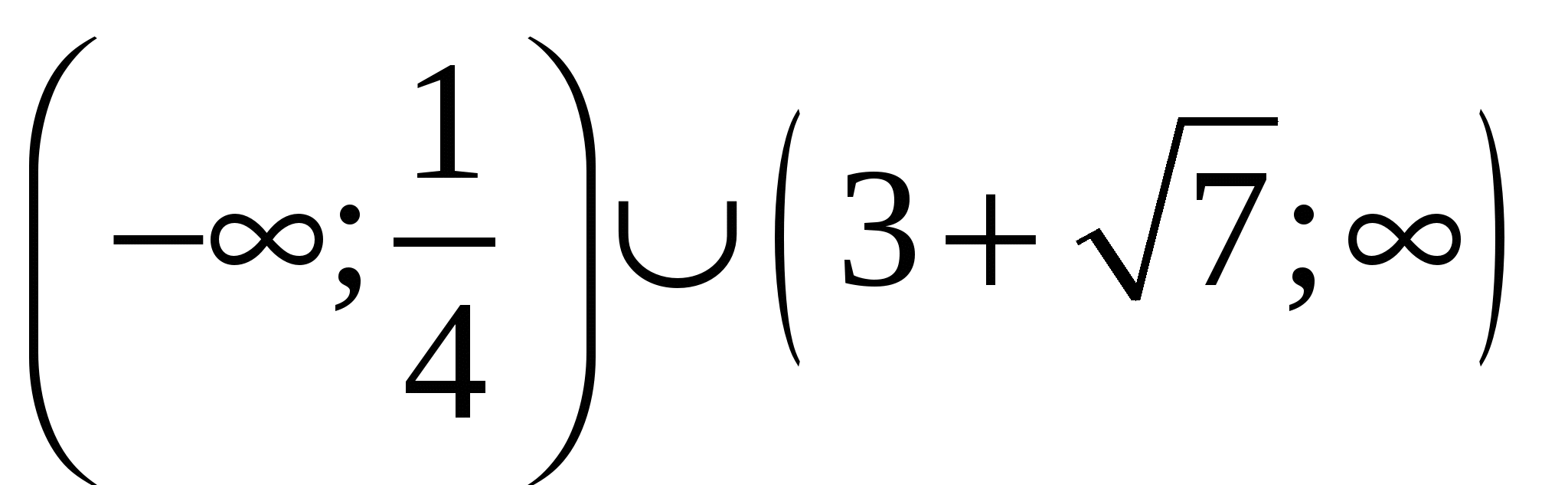
|
Найдите все значения a, при каждом из которых все решения неравенства 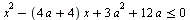 удовлетворяют неравенству удовлетворяют неравенству 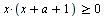 . .
|
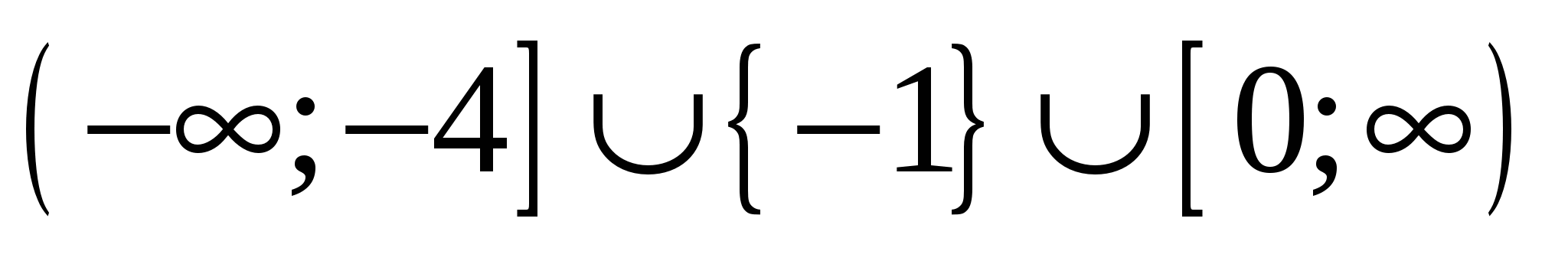
|
Найдите наибольшее значение параметра a, при котором функция 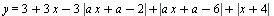 является неубывающей на всей числовой прямой. является неубывающей на всей числовой прямой.
|
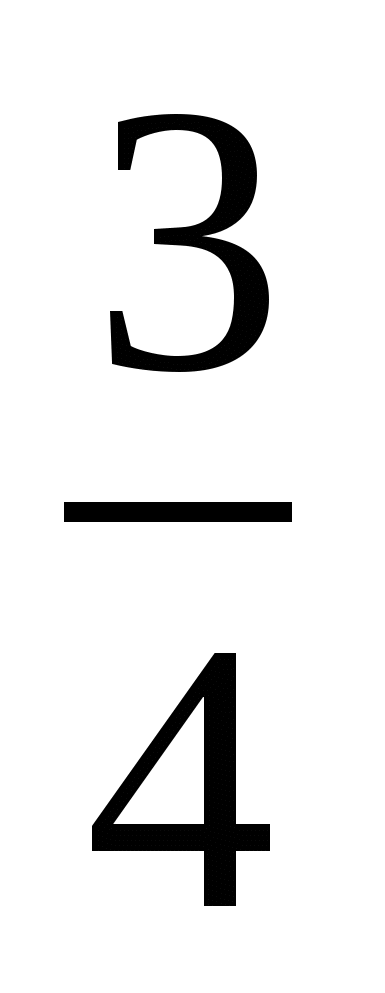
|
Найдите все значения a, при каждом из которых уравнение 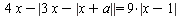 имеет хотя бы один корень. имеет хотя бы один корень.
|
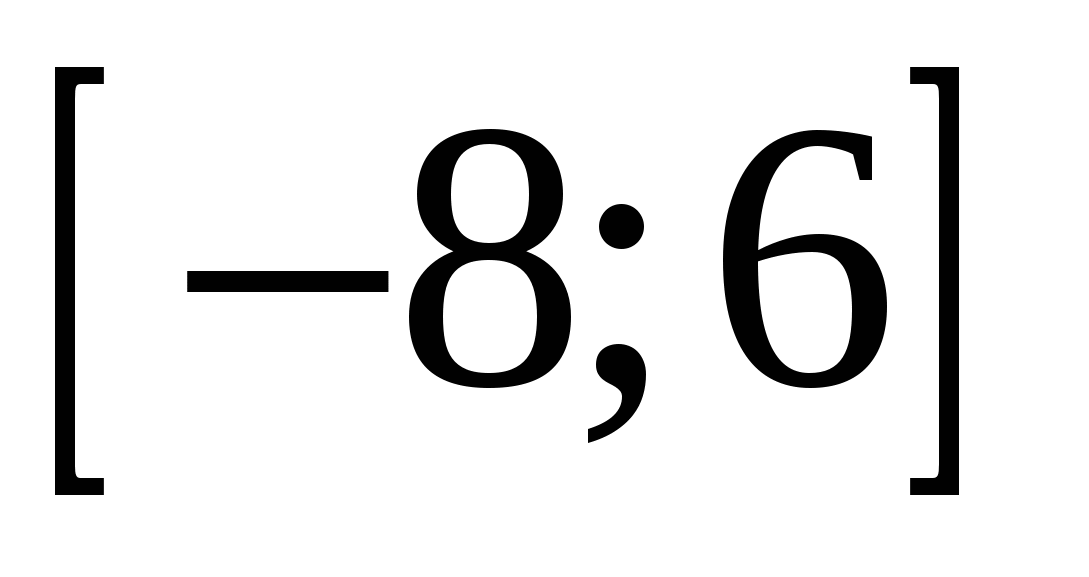
|
Найдите все значения параметра а, при каждом из которых система 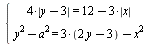 имеет ровно 4 решения. имеет ровно 4 решения.
|
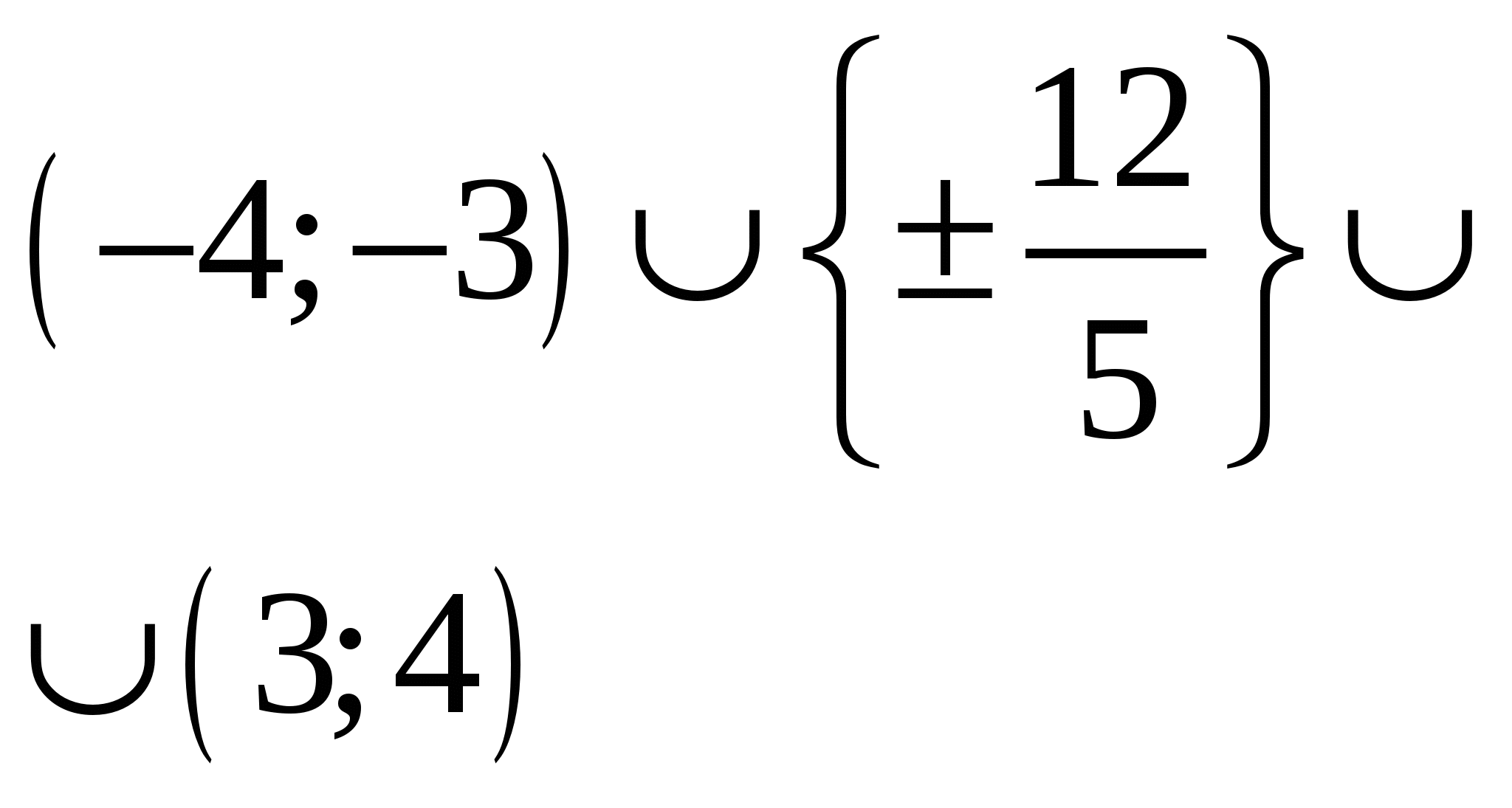
|
Найдите все значения параметра а, при которых система 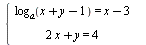 имеет единственное решение. имеет единственное решение.
|
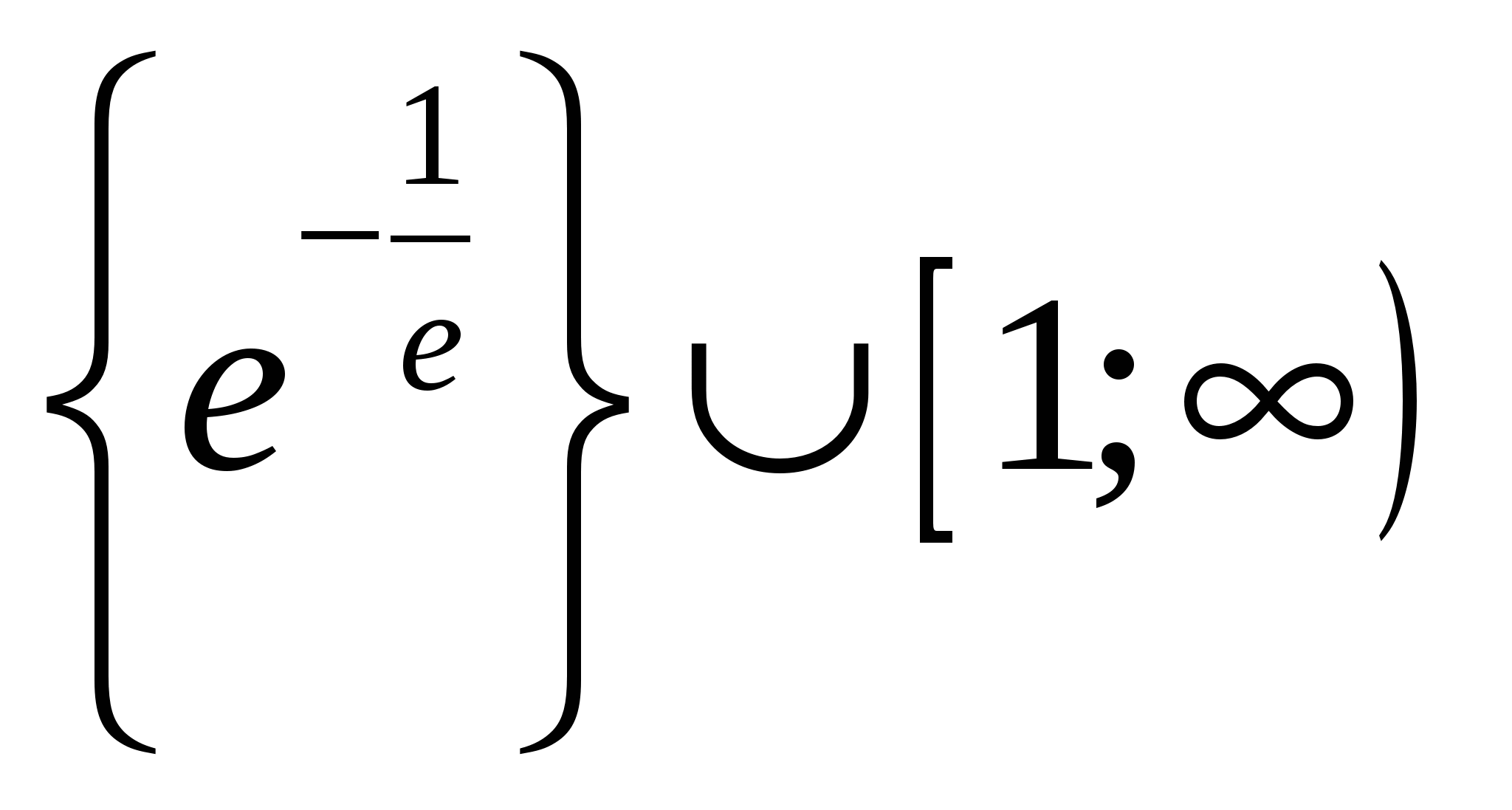
|
Для каждого значения 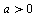 найдите уравнения всех прямых, проходящих через начало координат и имеющих ровно две общие точки с графиком функции найдите уравнения всех прямых, проходящих через начало координат и имеющих ровно две общие точки с графиком функции 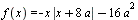 . .
|
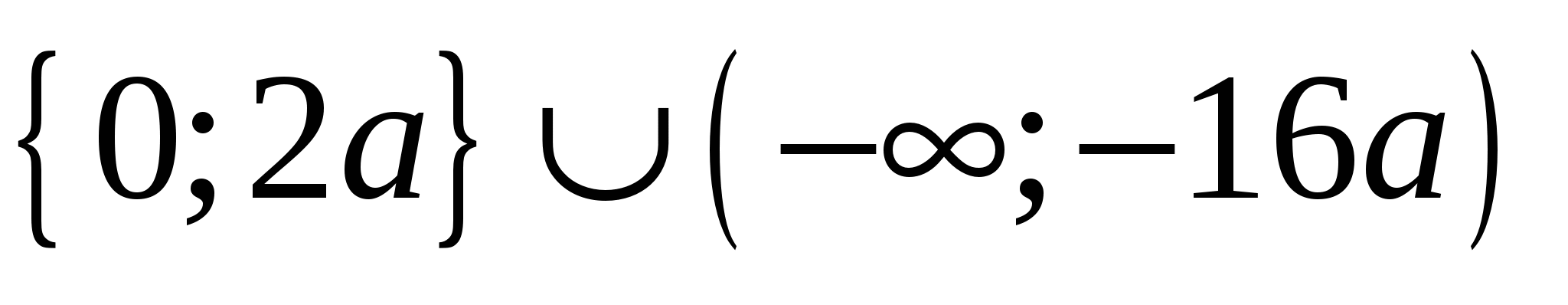
|
Известно, что значение параметра a таково, что система уравнений 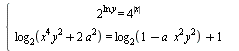 имеет единственное решение. Найдите это значение параметра a и решите систему при найденном значении параметра. имеет единственное решение. Найдите это значение параметра a и решите систему при найденном значении параметра.
|
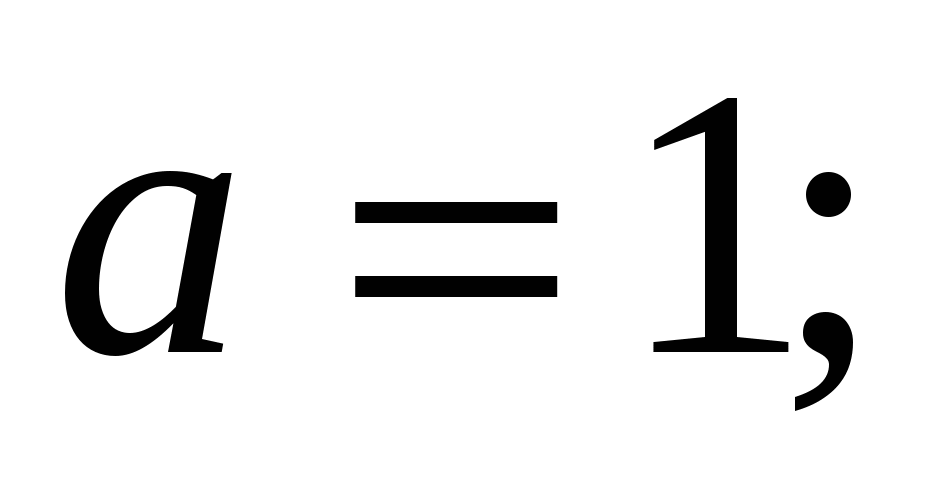 решение решение 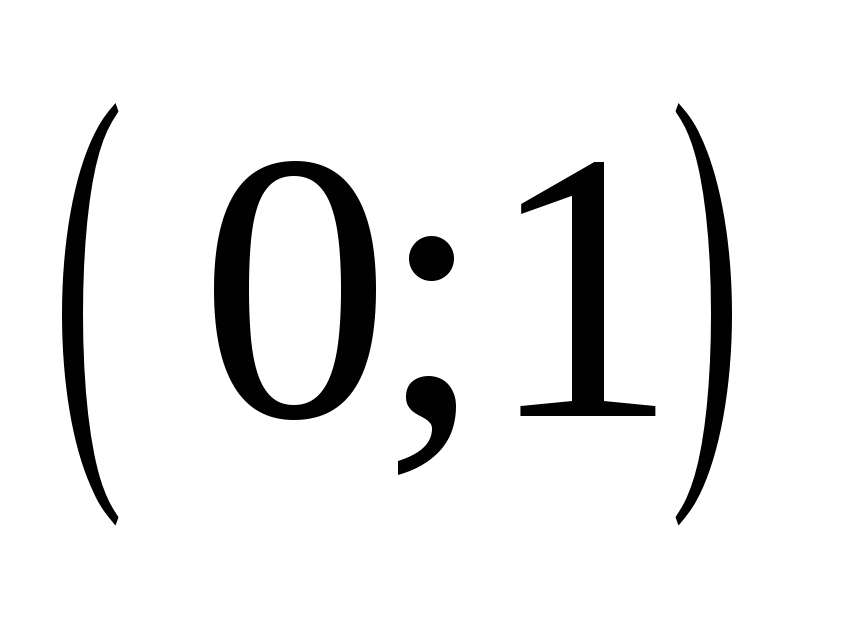
|
Определить, при каких значениях параметра b для любых значений параметра a система уравнений 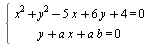 имеет ровно два различных решения (x ; y ) . имеет ровно два различных решения (x ; y ) .
|
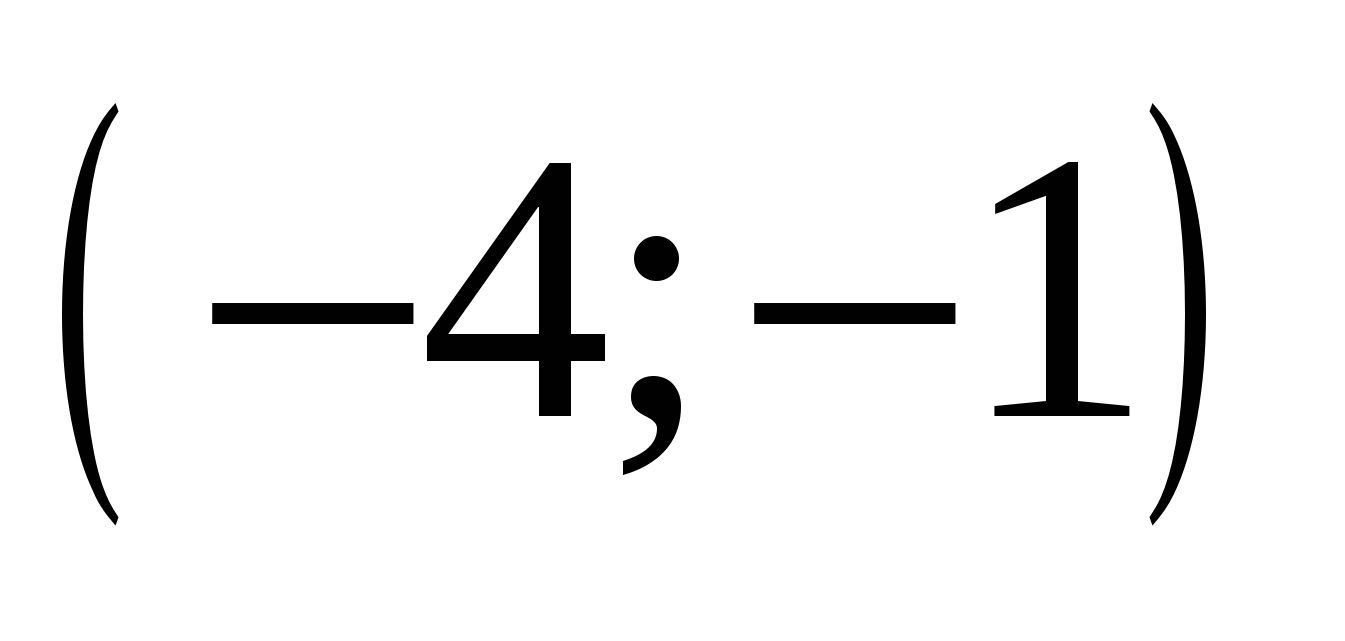
|
Найдите все значения параметра а, при которых общие решения неравенств 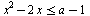 и и 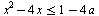 образуют на числовой оси отрезок длины единица. образуют на числовой оси отрезок длины единица.
|
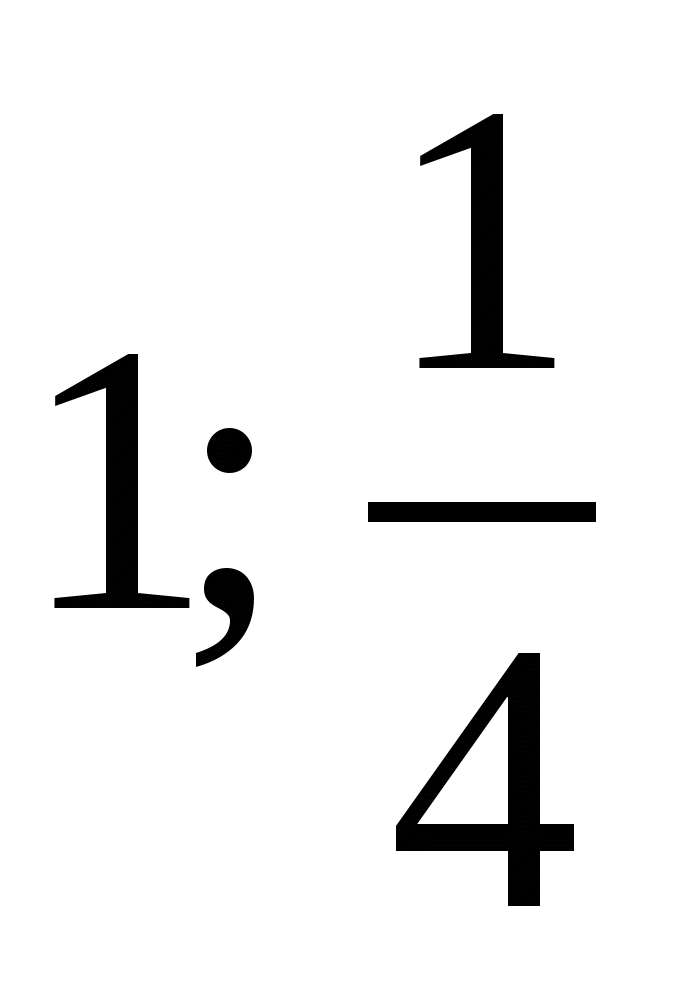
|
Найдите все значения а, при каждом из которых любая прямая, перпендикулярная оси ординат, имеет нечетное число общих точек с графиком функции 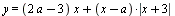 . .
|
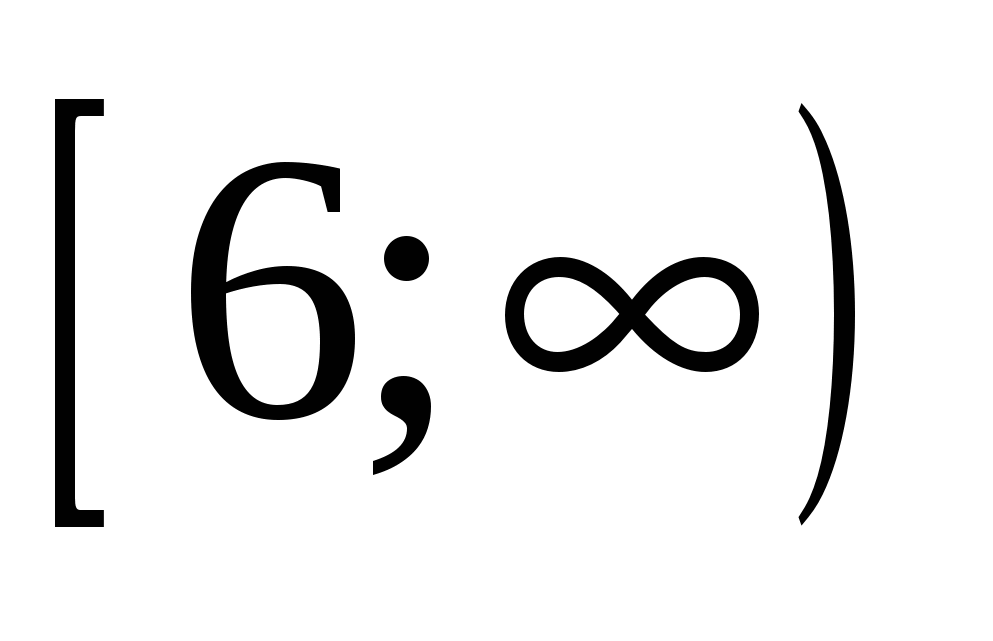
|
Найдите все значения а , при каждом из которых существует прямая, перпендикулярная оси ординат и имеющая четное число общих точек с графиком функции 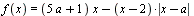 . .
|
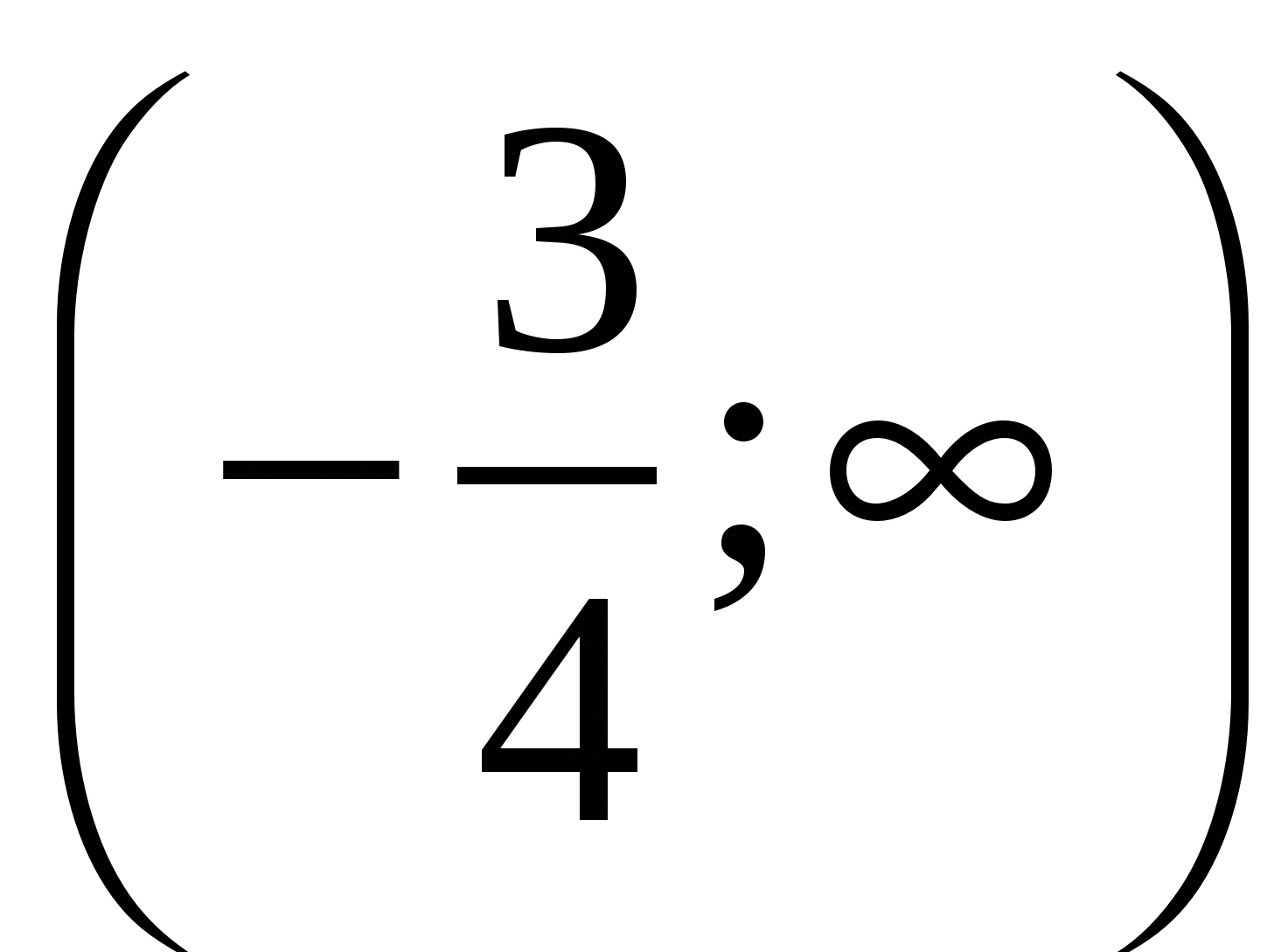
|
Найти все значения а, для которых при каждом х из промежутка [−2;−1) значение выражения 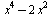 не равно значению выражения не равно значению выражения 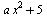 . .
|
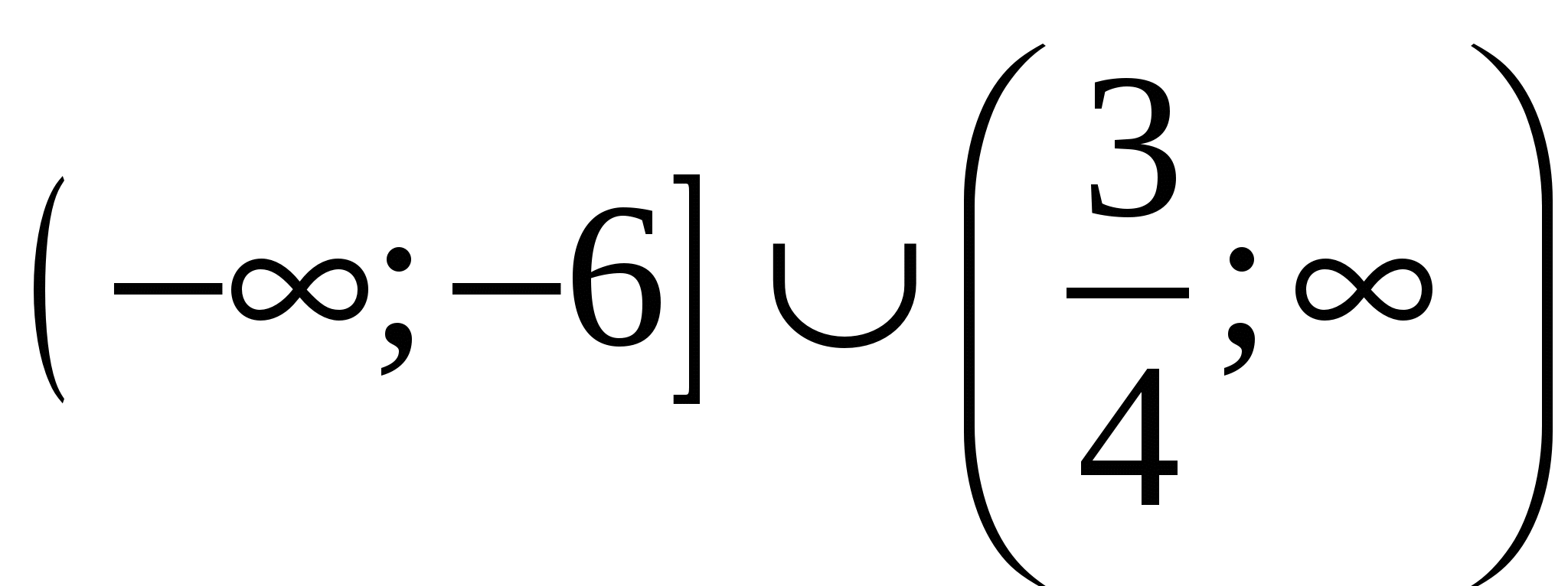
|
Найдите все значения параметра а, при которых система 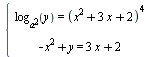 имеет ровно два решения. имеет ровно два решения.
|
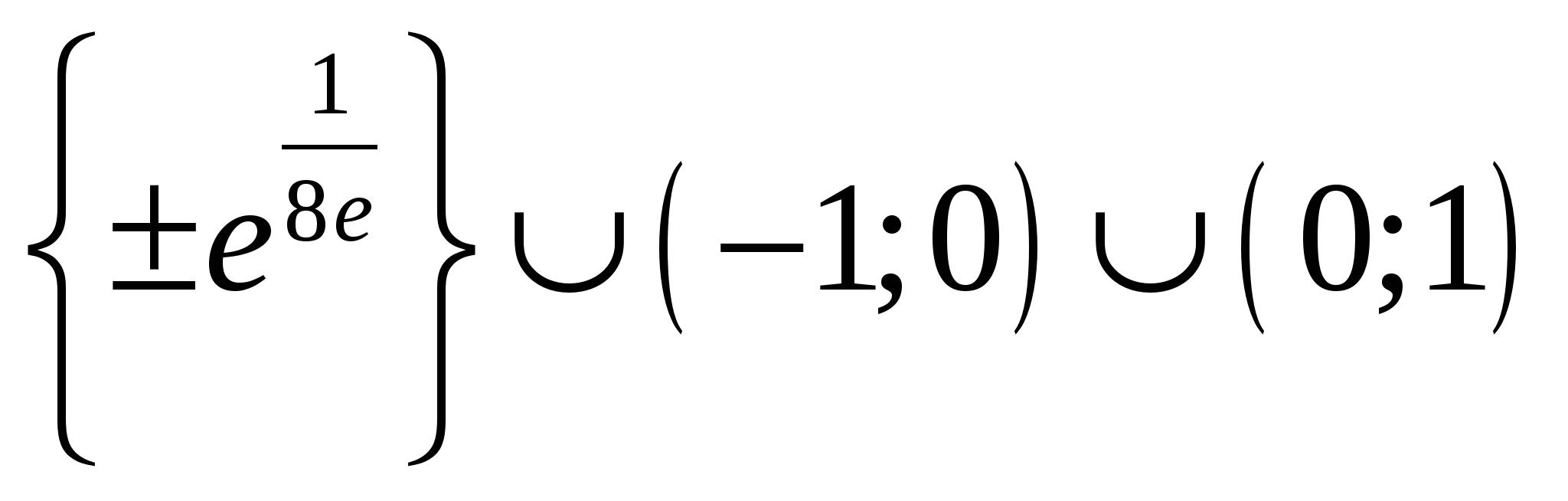
|
Найдите все значения параметра p, при каждом из которых уравнение 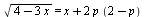 имеет ровно р корней. имеет ровно р корней.
|
1
|
Найдите все значения параметра а, при которых система 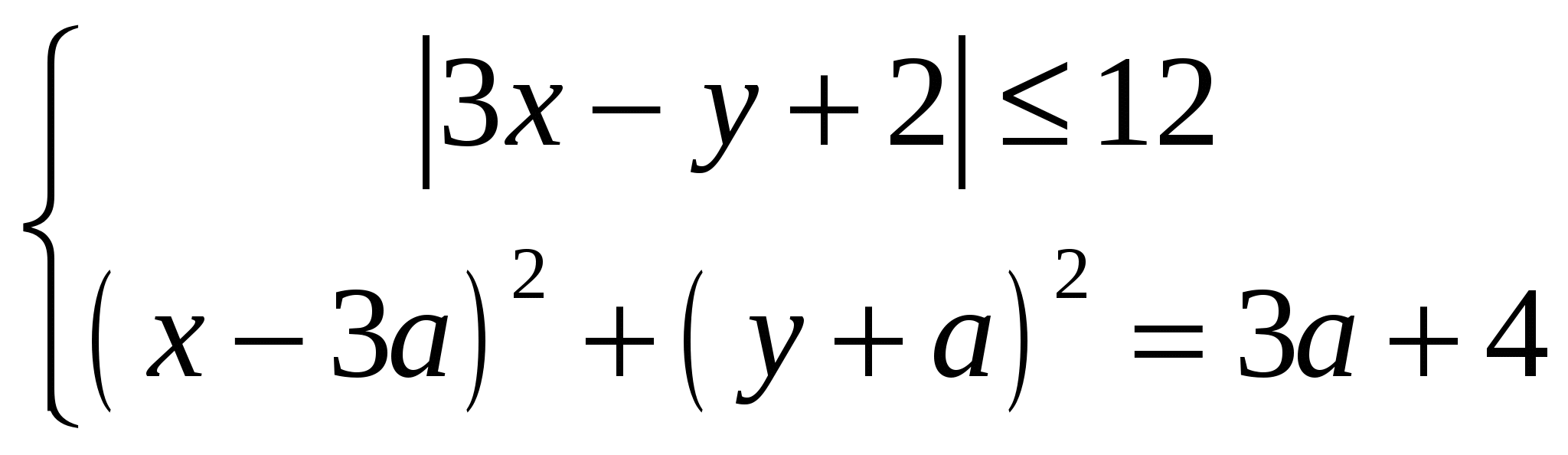 имеет единственное решение. имеет единственное решение.
|
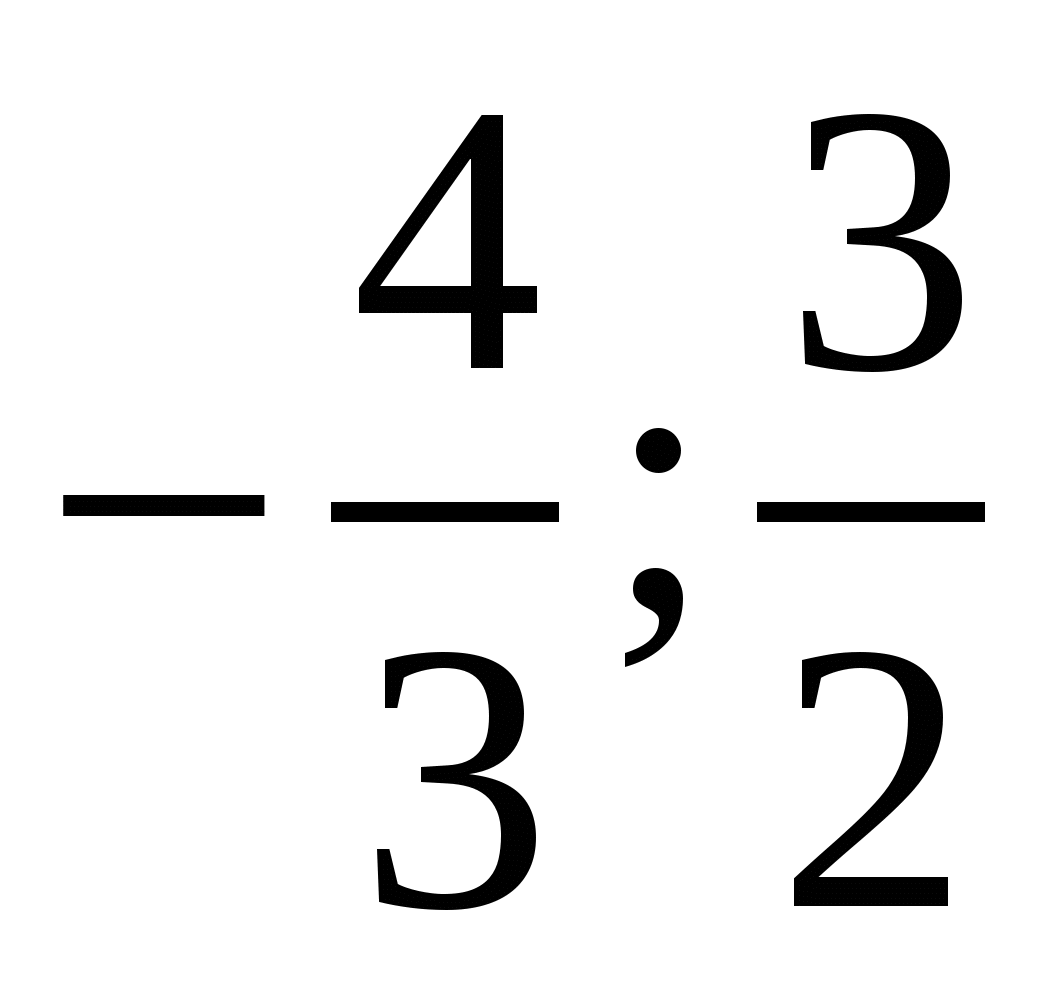
|
Пусть А - множество тех значений параметра а, для которых выполнено условие 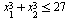 , где , где 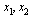 - действительные, различные корни уравнения - действительные, различные корни уравнения 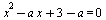 . Найдите множество значений, которое при этих условиях принимает величина . Найдите множество значений, которое при этих условиях принимает величина 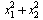 . .
|
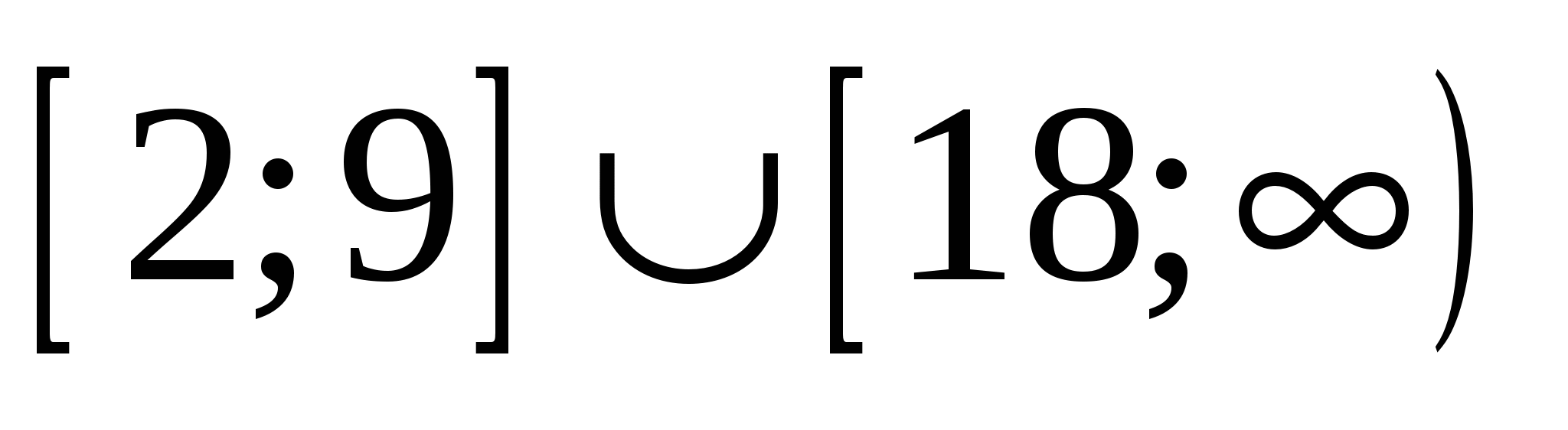
|
При каких значениях параметра  множество решений неравенства множество решений неравенства 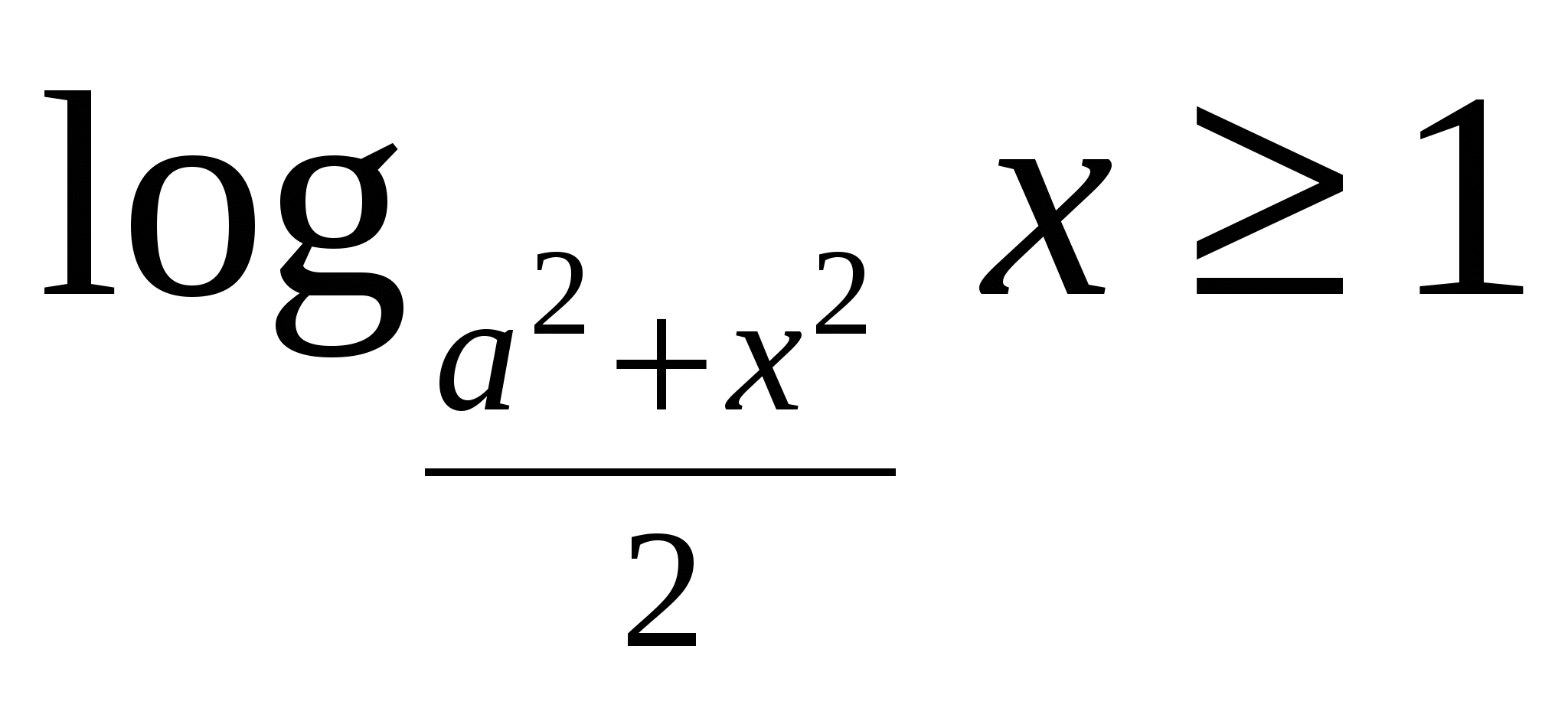 содержит не менее двух решений уравнения содержит не менее двух решений уравнения 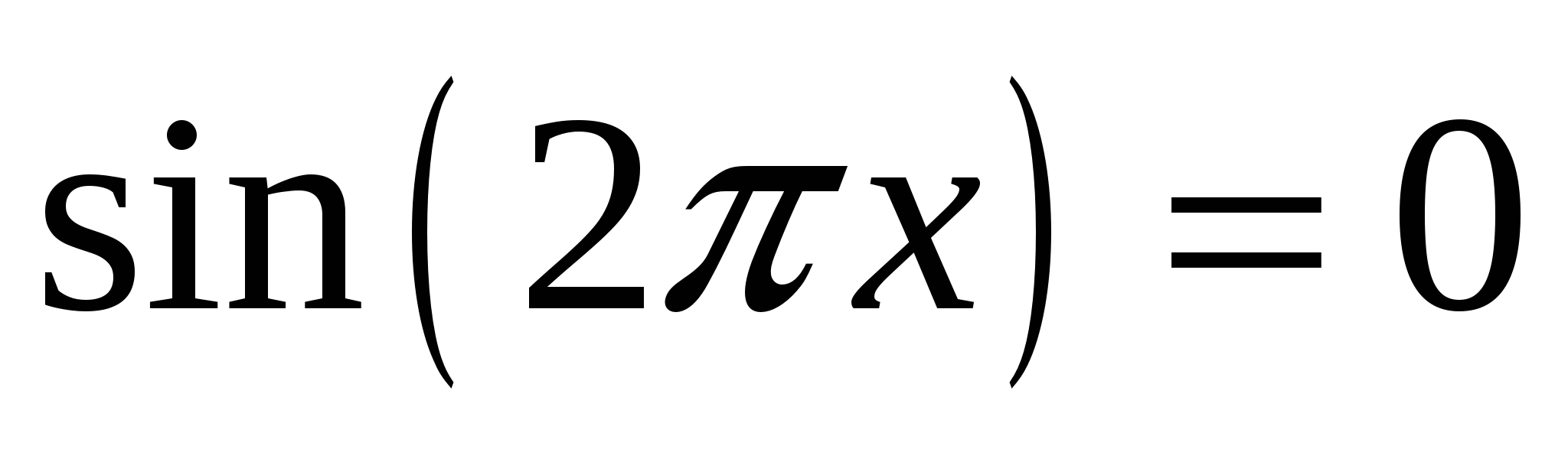 ? ?
|
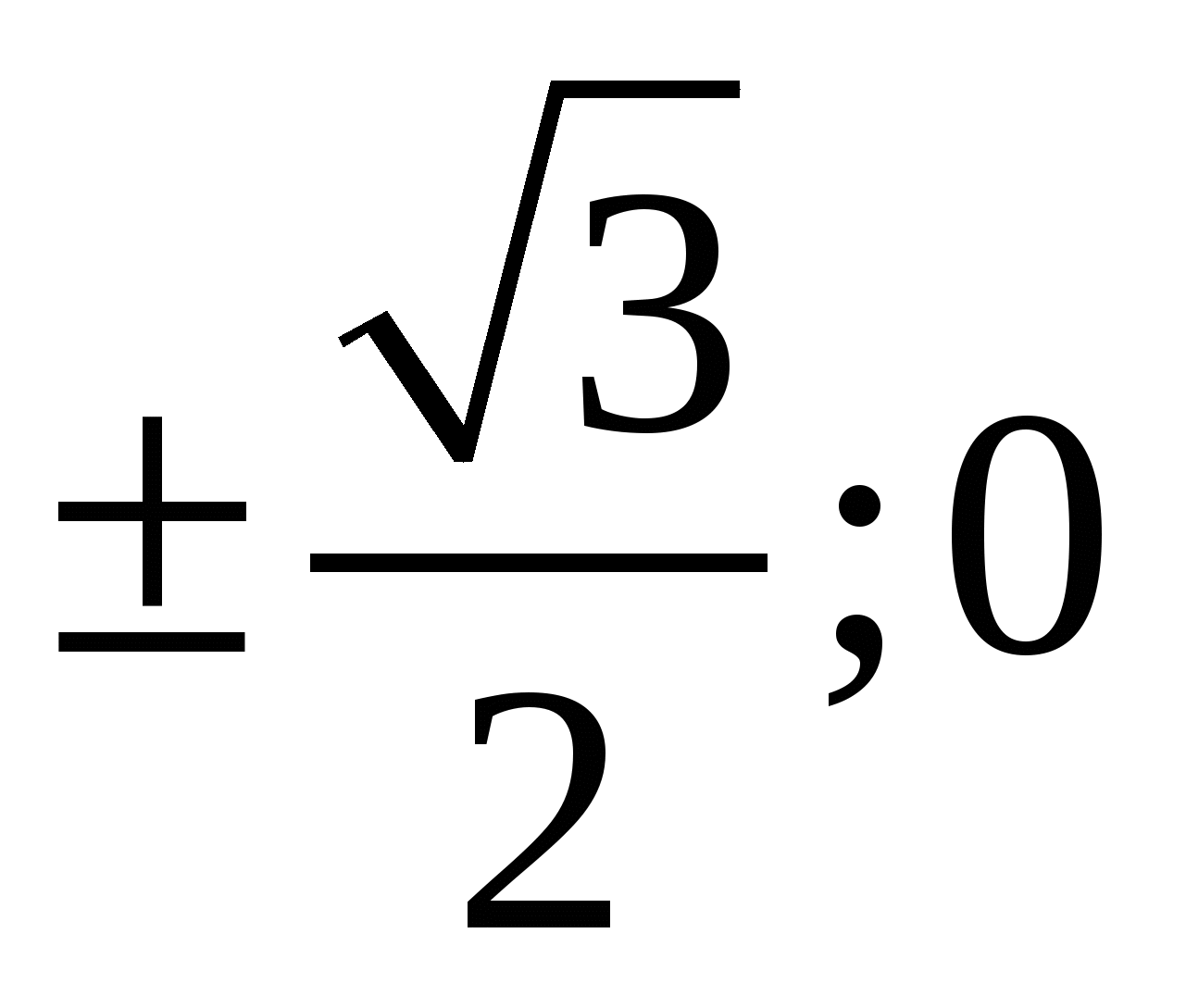
|
Найдите все значения параметра  , при каждом из которых множеством решений неравенства , при каждом из которых множеством решений неравенства 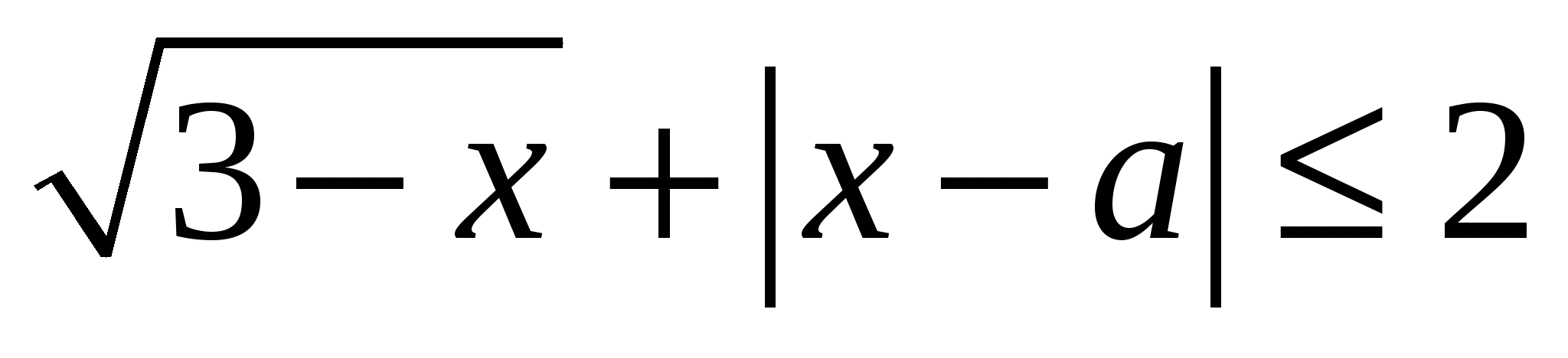 является отрезок. является отрезок.
|
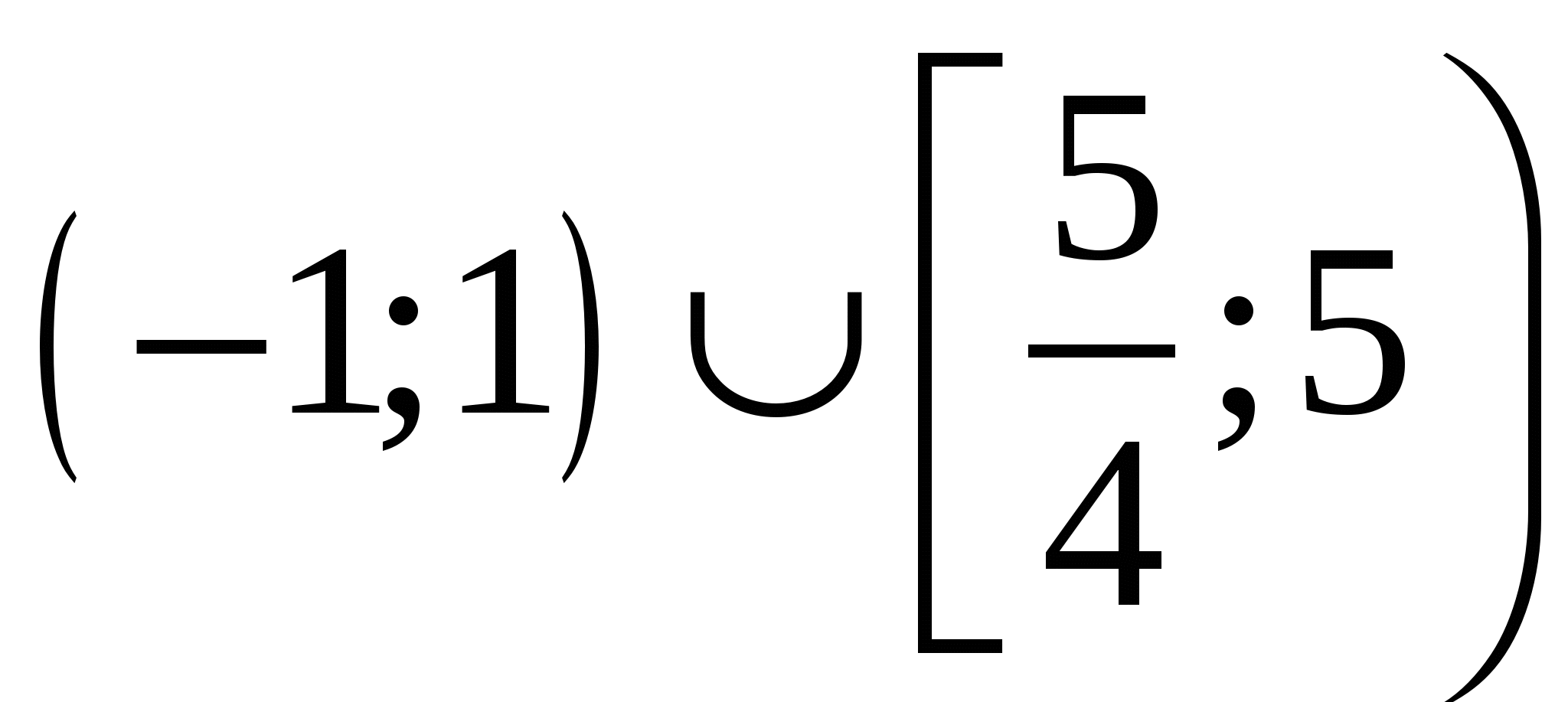
|
Блок 3. (домашнее задание)
|
Найдите все значения  , при каждом из которых уравнение , при каждом из которых уравнение 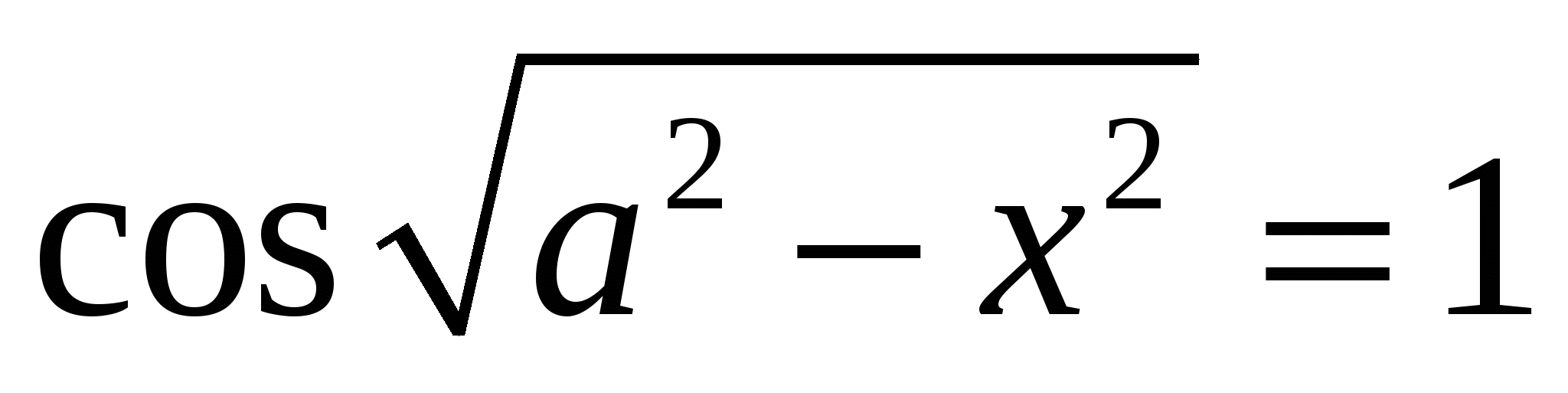 имеет ровно 6 решений. имеет ровно 6 решений.
|
|
Найдите все значения  , при каждом из которых уравнение , при каждом из которых уравнение 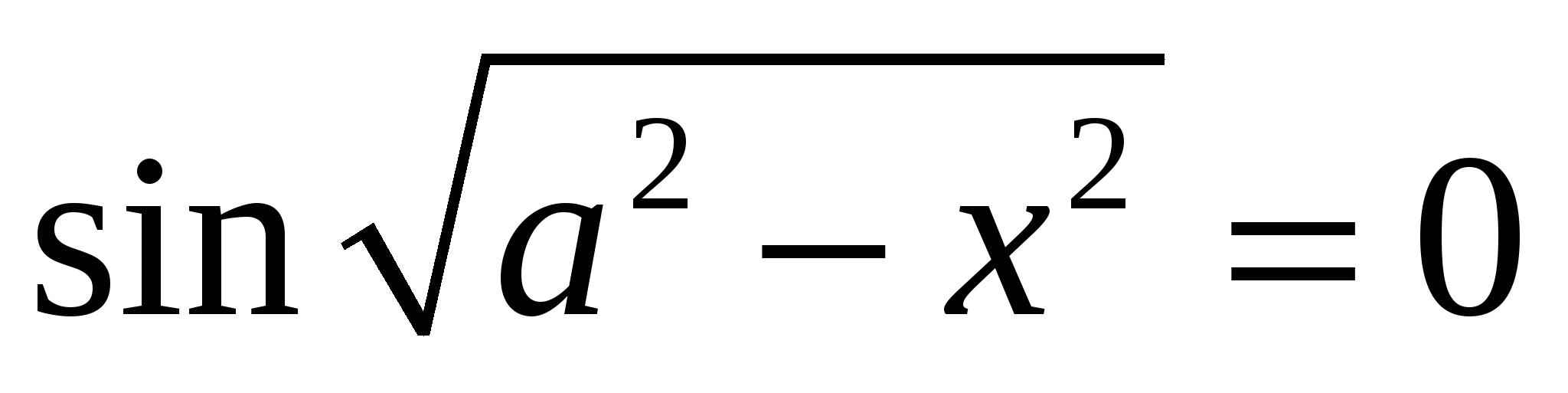 имеет ровно 10 решений. имеет ровно 10 решений.
|
|
Найдите все значения а, при каждом из которых система 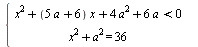 имеет решения. имеет решения.
|
|
Найдите все значения а, при каждом из которых система 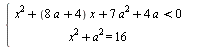 имеет решения. имеет решения.
|
|
Найдите все значения параметра а, при которых функция 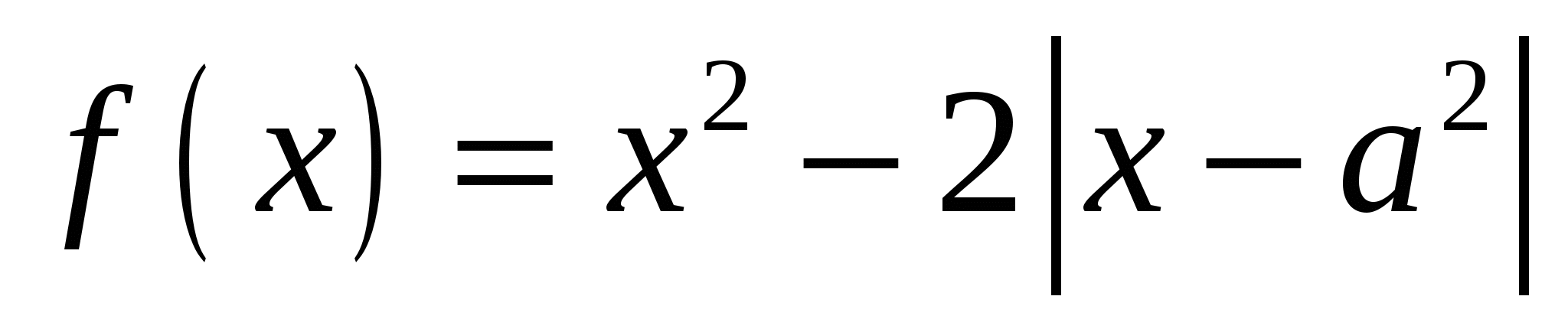 имеет хотя бы одну точку максимума. имеет хотя бы одну точку максимума.
|
|
Найдите все значения а, при которых система 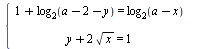 имеет решения. имеет решения.
|
|
Найдите все положительные значения а, при каждом из которых система 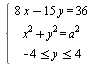 имеет единственное решение. имеет единственное решение.
|
|
Найдите все значения параметра a , при которых система уравнений 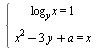 имеет два решения. имеет два решения.
|
|
Найдите все значения a, при каждом из которых функция 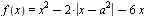 имеет более двух точек экстремума. имеет более двух точек экстремума.
|
|
Найдите все значения a, при каждом из которых наименьшее значение функции 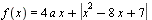 меньше 1. меньше 1.
|
|
Найдите все значения a, при каждом из которых наименьшее значение функции 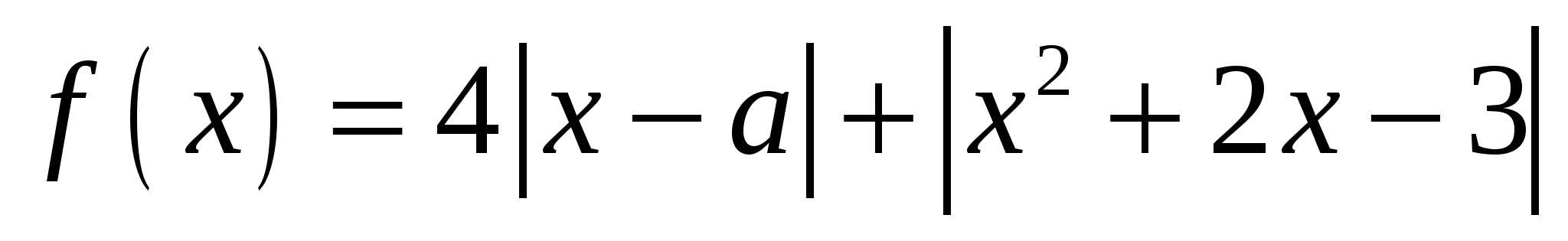 меньше 4. меньше 4.
|
|
Найдите все значения а, при каждом из которых ровно одно решение неравенства 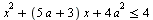 удовлетворяет неравенству удовлетворяет неравенству 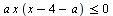 . .
|
|
Найдите наименьшее значение параметра a, при котором функция 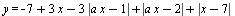 является неубывающей на всей числовой прямой. является неубывающей на всей числовой прямой.
|
|
Найдите все значения параметра а, при каждом из которых система 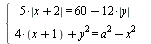 имеет ровно 8 решения. имеет ровно 8 решения.
|
|
Найдите все значения параметра а, при каждом из которых система 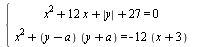 имеет ровно 4 решения. имеет ровно 4 решения.
|
|
Найдите все значения параметра а, при каждом из которых система 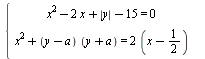 имеет ровно 6 решений. имеет ровно 6 решений.
|
|
Найдите все значения а, при каждом из которых любая прямая, перпендикулярная оси ординат, имеет нечетное число общих точек с графиком функции 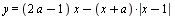 . .
|
|
Найдите все значения параметра а, при которых система 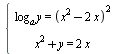 имеет ровно два решения. имеет ровно два решения.
|
|
Найдите все значения параметра а, при которых система 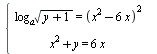 имеет ровно два решения. имеет ровно два решения.
|
|
Найдите все значения параметра а, при которых система неравенств 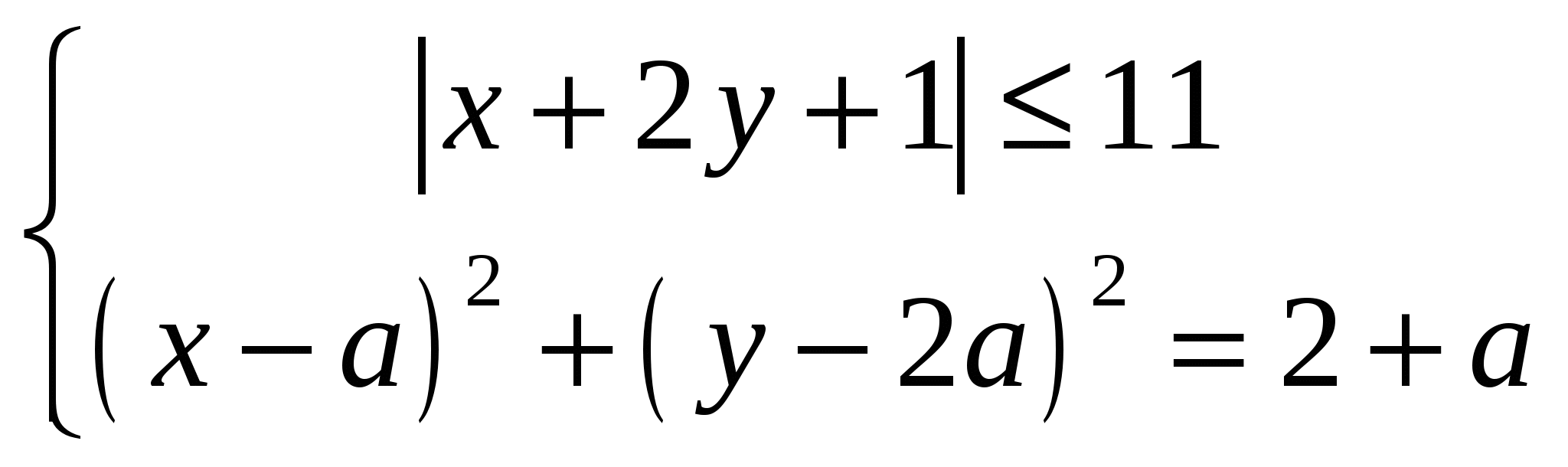 имеет единственное решение. имеет единственное решение.
|
|
Найдите все значения параметра а, при каждом из которых система 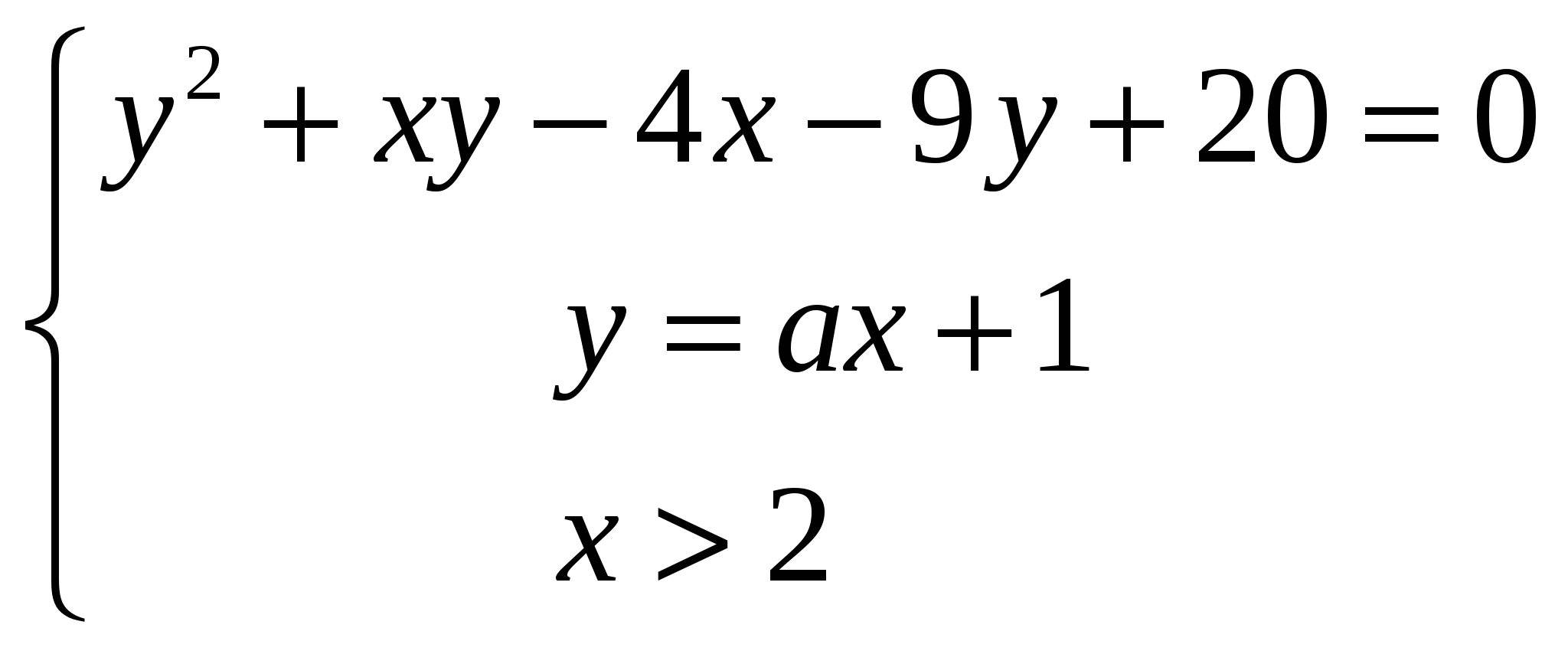 имеет единственное решение. имеет единственное решение.
|
|
Найдите все значения параметра а, при которых система 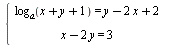 имеет единственное решение. имеет единственное решение.
|
|
При каких значениях параметра  множество решений неравенства множество решений неравенства 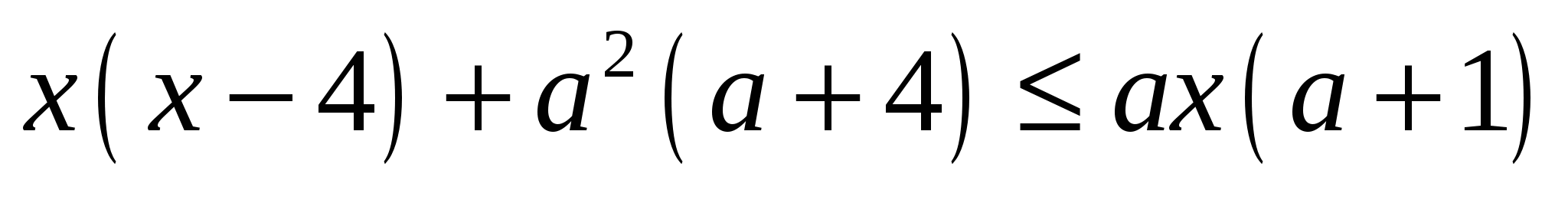 содержит не более четырех целых значений содержит не более четырех целых значений 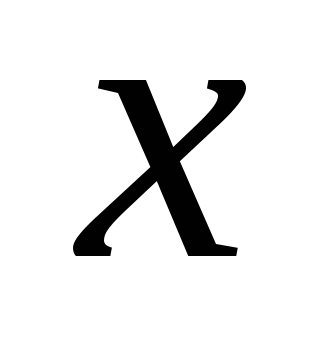 ? ?
|
|
Найдите все значения параметра  , при каждом из которых множеством решений неравенства , при каждом из которых множеством решений неравенства 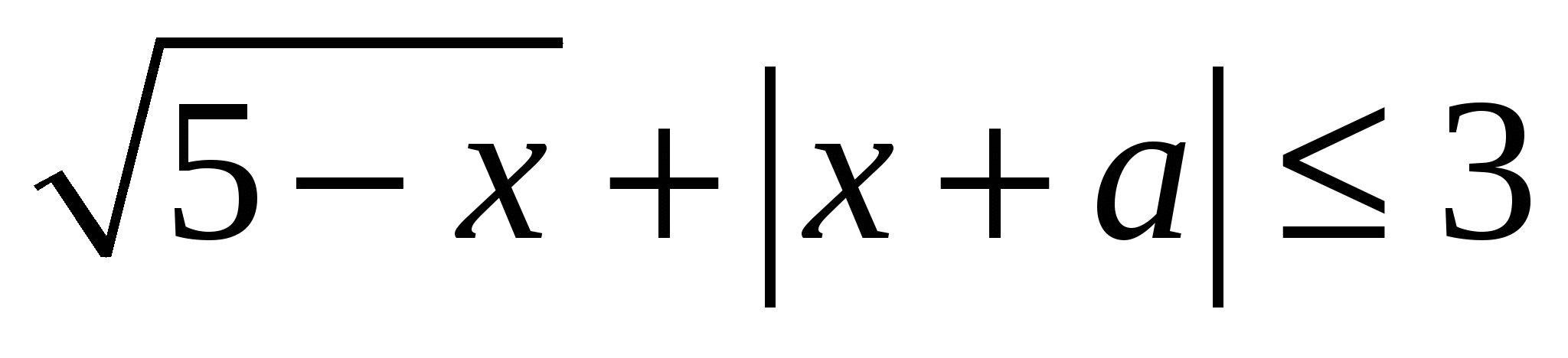 является отрезок. является отрезок.
|
|
Найдите все значения параметра а, при которых система 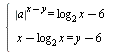 имеет ровно два решения. имеет ровно два решения.
|
| |
|
|
 Скачать 103.43 Kb.
Скачать 103.43 Kb.
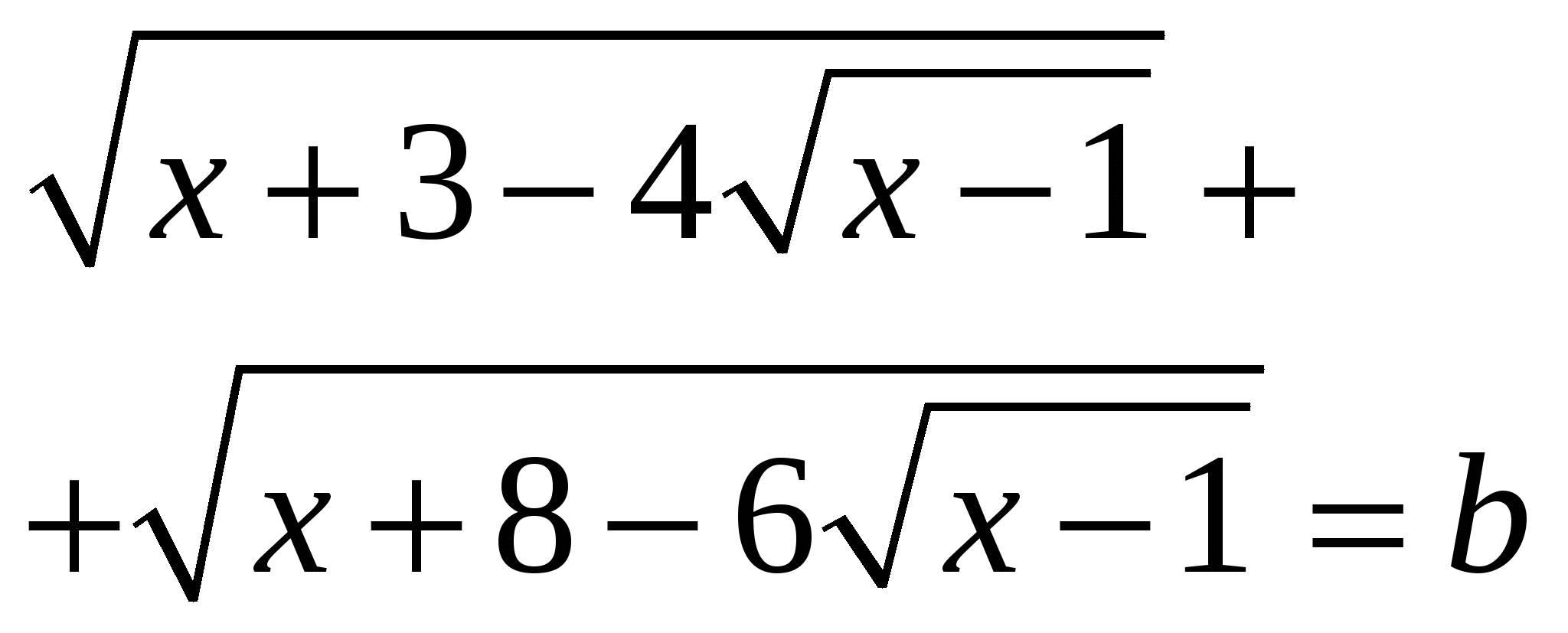 существуют и принадлежат отрезку |2;17].
существуют и принадлежат отрезку |2;17]. 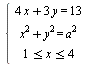 имеет единственное решение.
имеет единственное решение. 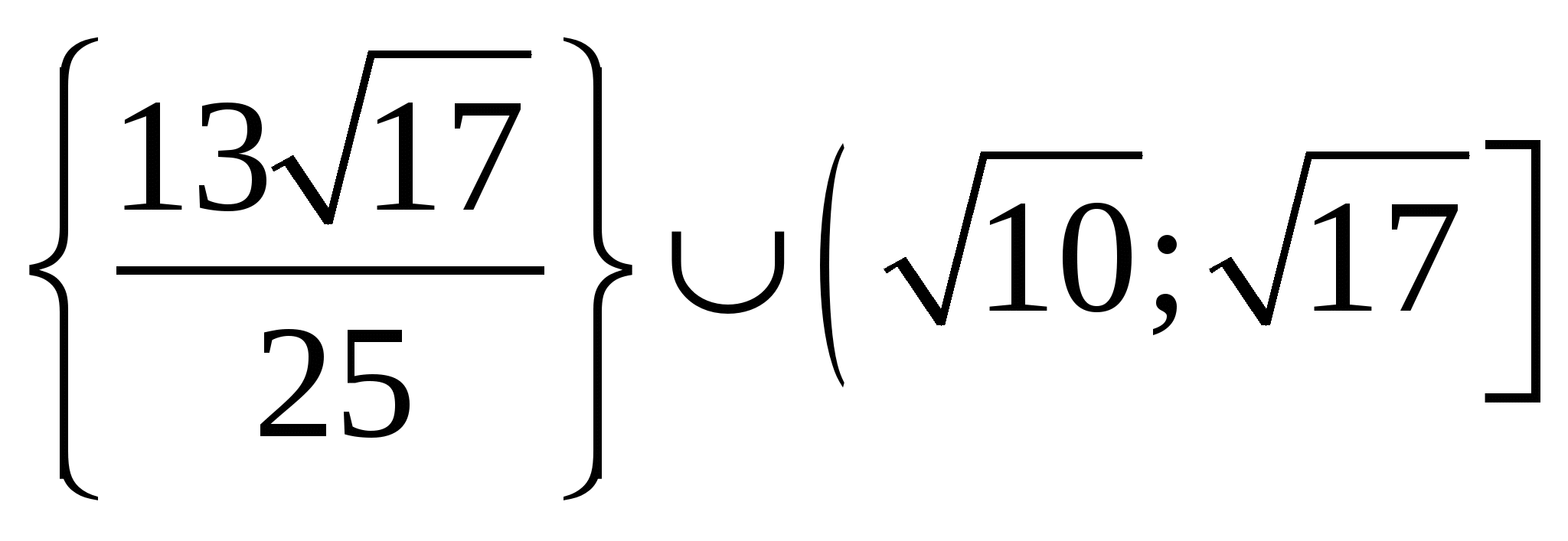
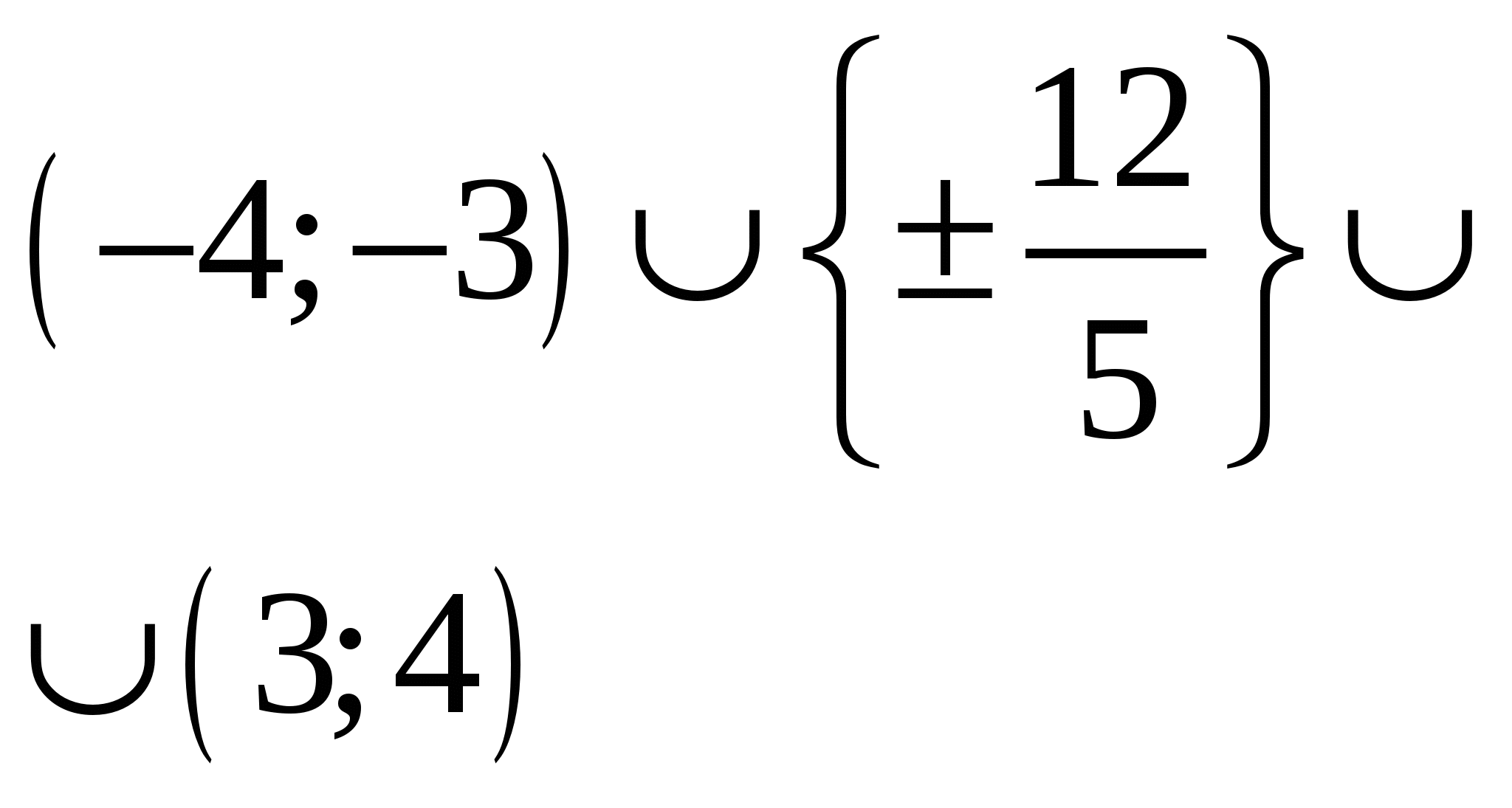
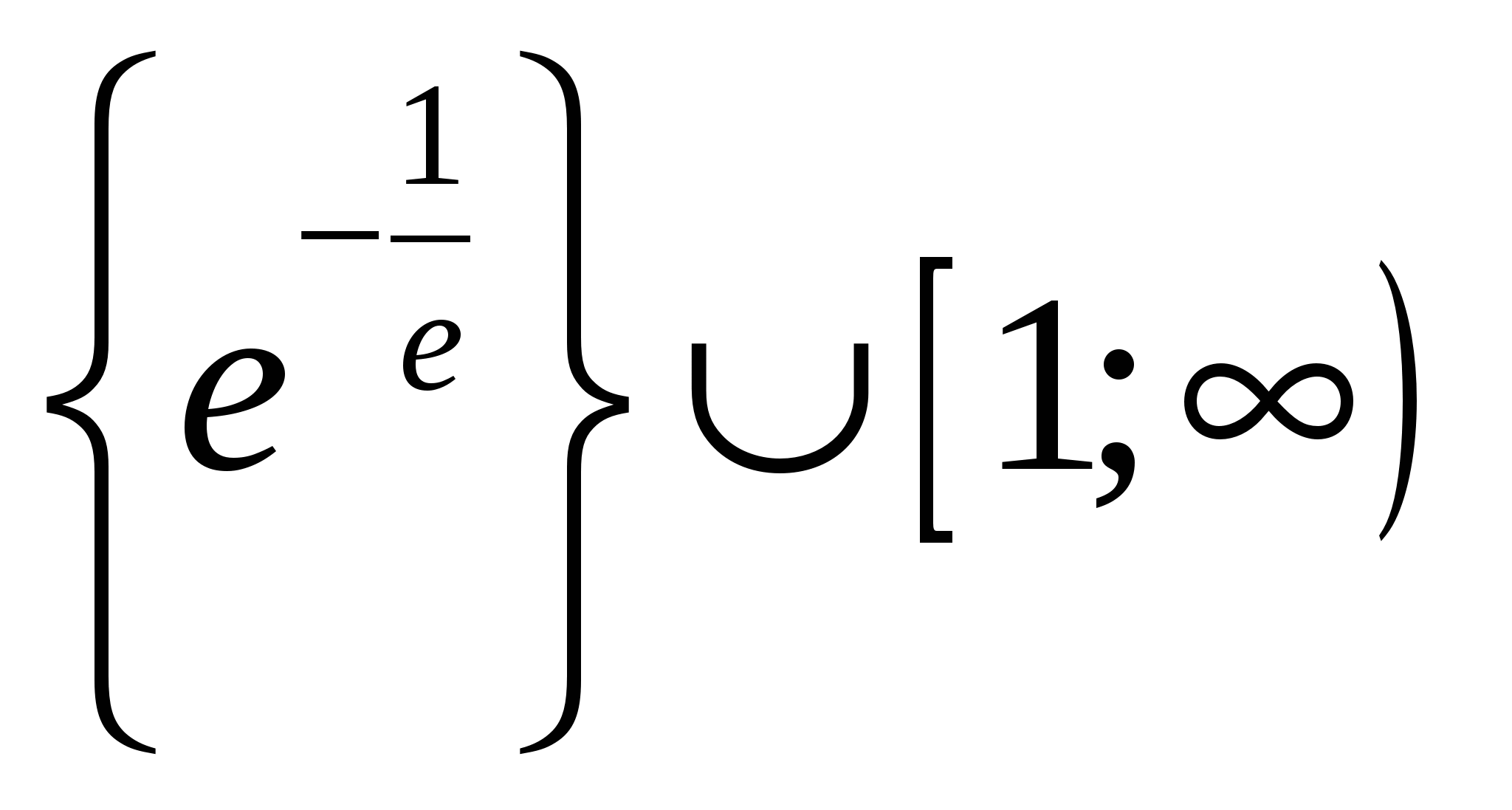
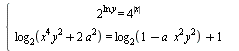 имеет единственное решение. Найдите это значение параметра a и решите систему при найденном значении параметра.
имеет единственное решение. Найдите это значение параметра a и решите систему при найденном значении параметра. 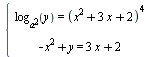 имеет ровно два решения.
имеет ровно два решения. 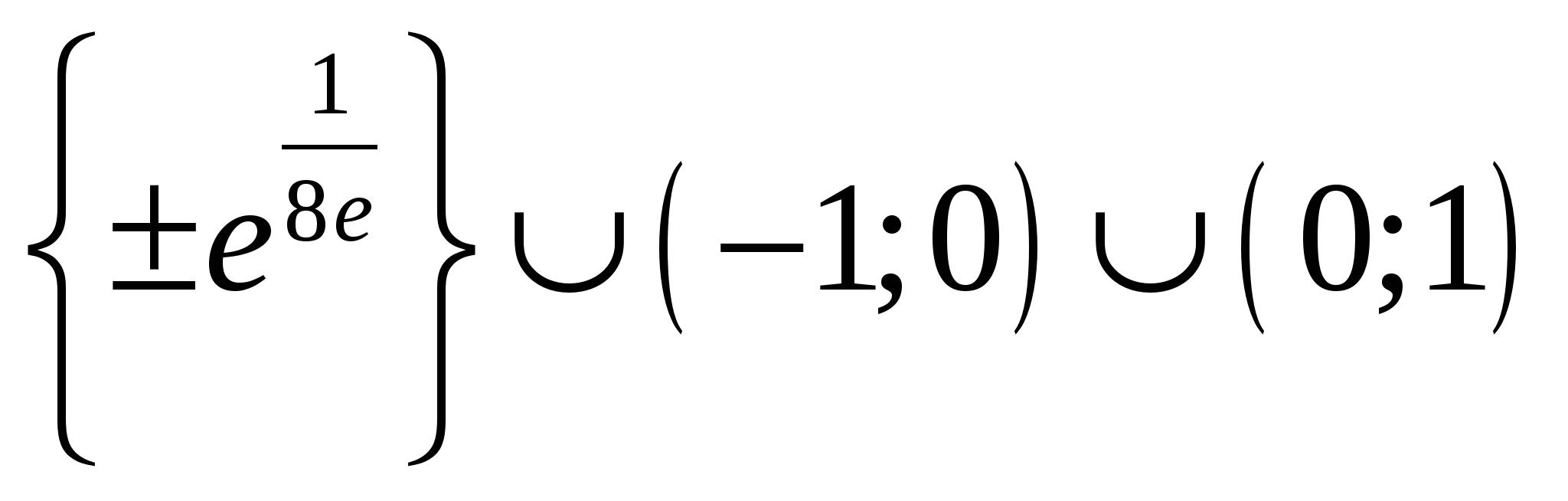
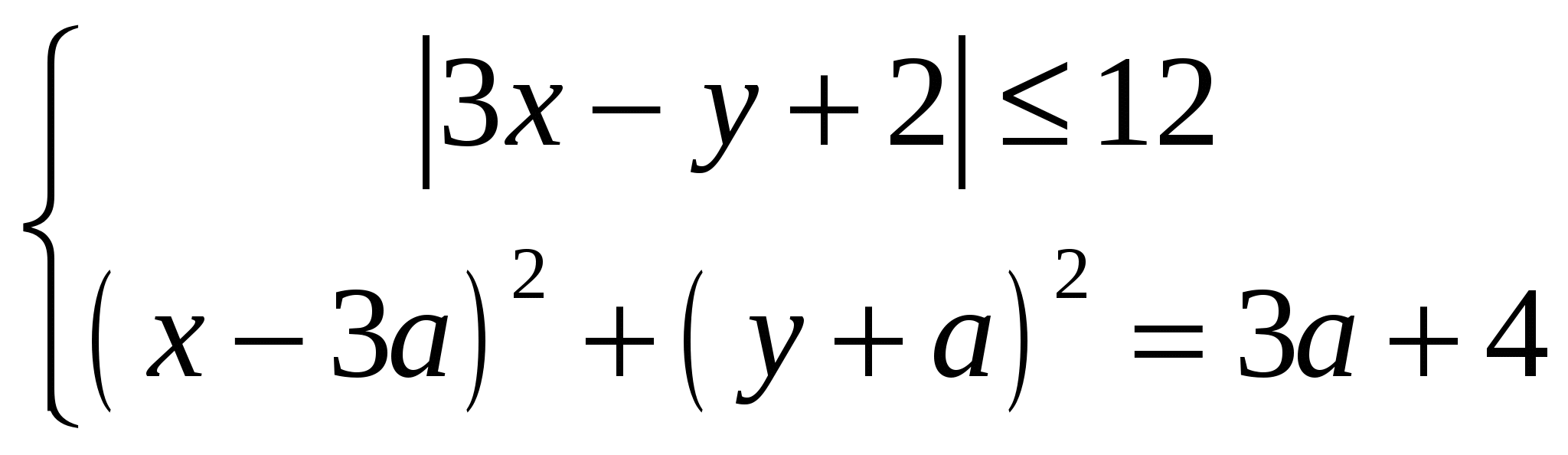 имеет единственное решение.
имеет единственное решение.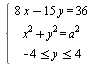 имеет единственное решение.
имеет единственное решение. 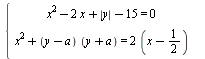 имеет ровно 6 решений.
имеет ровно 6 решений. 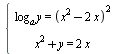 имеет ровно два решения.
имеет ровно два решения. 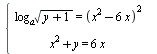 имеет ровно два решения.
имеет ровно два решения.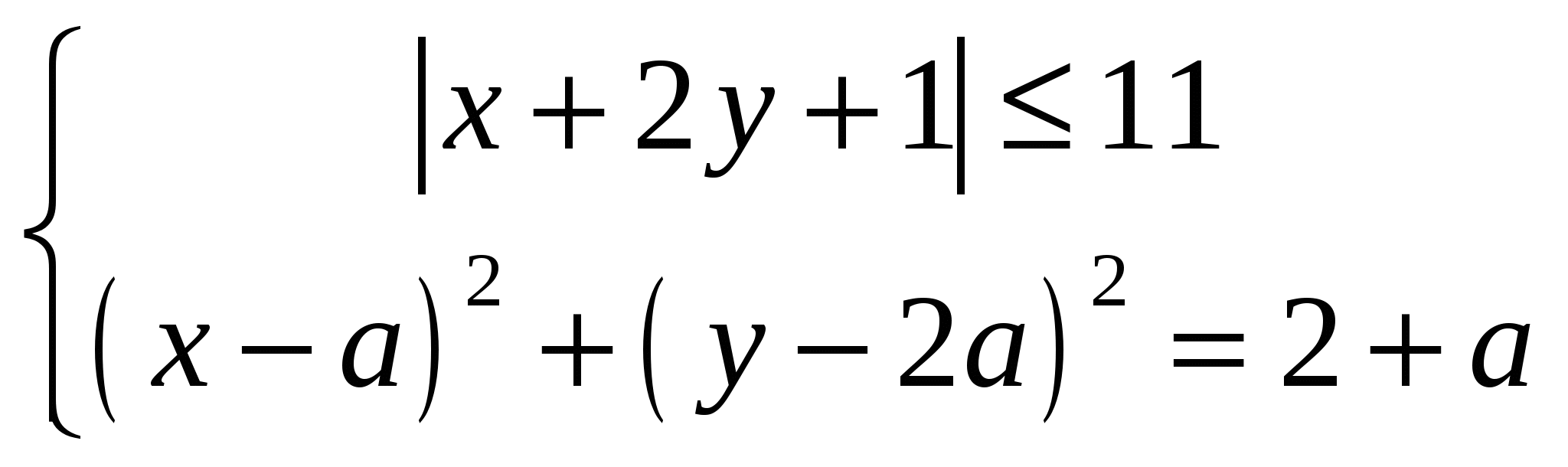 имеет единственное решение.
имеет единственное решение.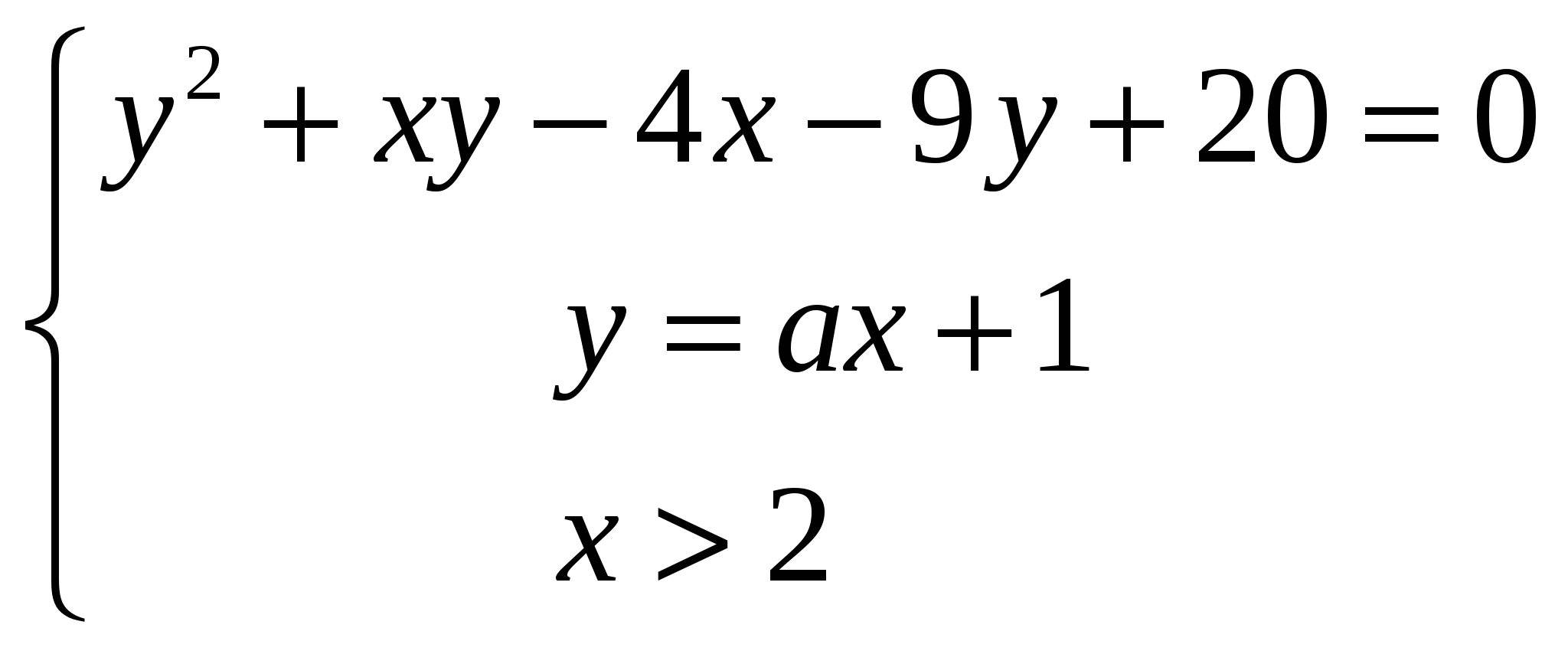 имеет единственное решение.
имеет единственное решение.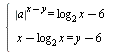 имеет ровно два решения.
имеет ровно два решения.