Задание
|
Комментарии
|
Ответ
|
Блок 1. (обязательный минимум-подготовка к задачам ЕГЭ)
|
При каждом значении а решите неравенство 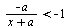 . .
|
Проще всего построить график неравенства в осях переменная-параметр. Не забывайте про пунктирные границы!
|
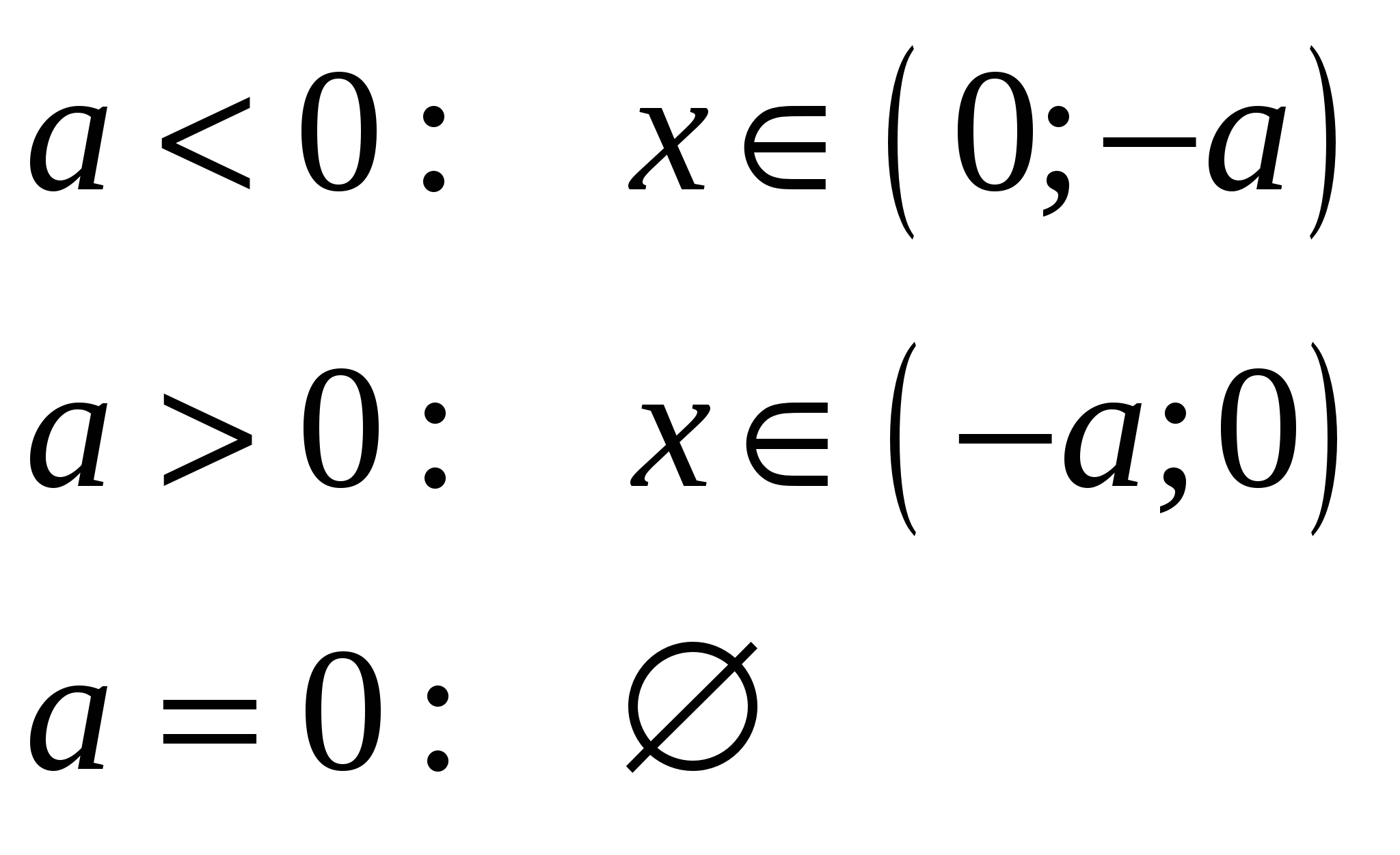
|
Найдите все значения параметра  , при каждом из которых график функции , при каждом из которых график функции 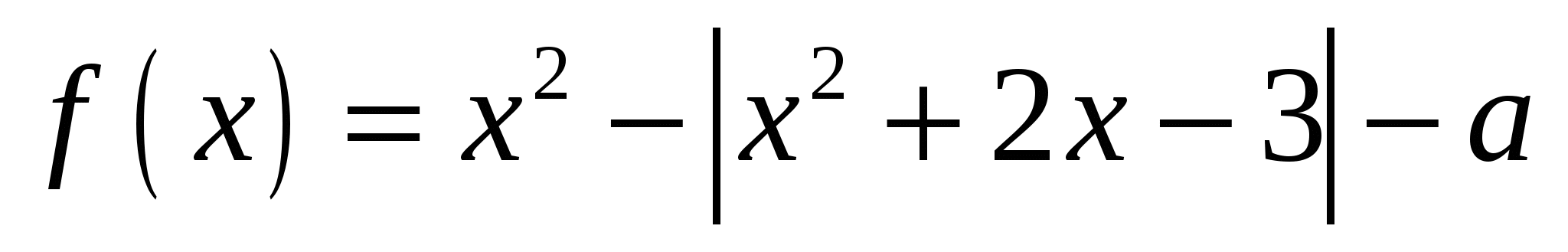 пересекает ось абсцисс более чем в двух различных точках. пересекает ось абсцисс более чем в двух различных точках.
|
В уравнении 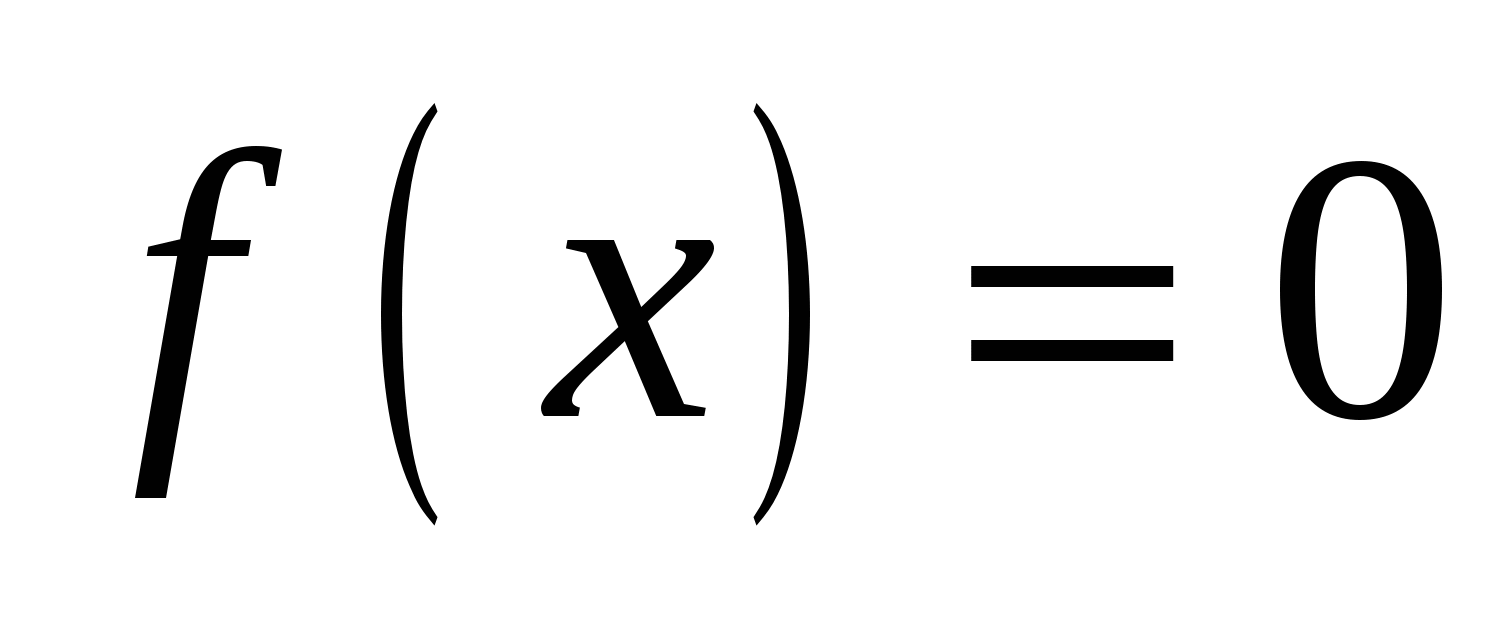 выразим параметр и построим график выразим параметр и построим график 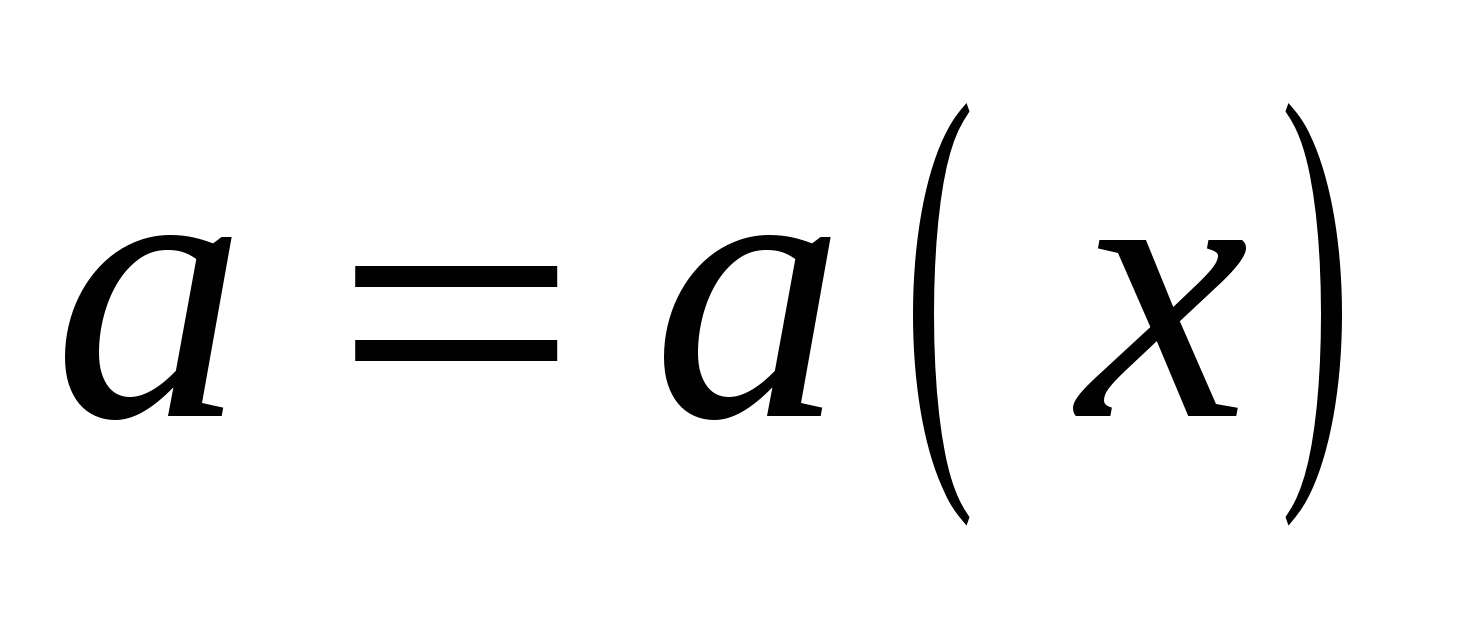 , после чего можно давать ответ. , после чего можно давать ответ.
|
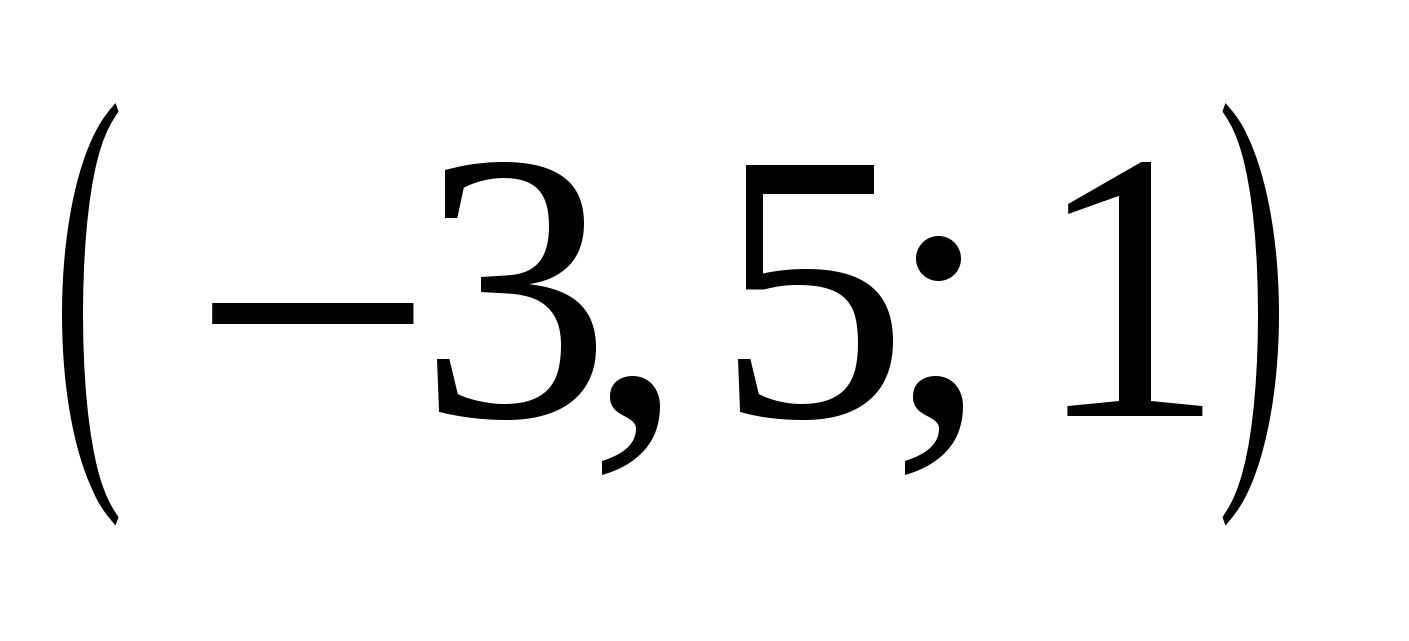
|
Найдите все значения параметра  , при каждом из которых неравенство , при каждом из которых неравенство 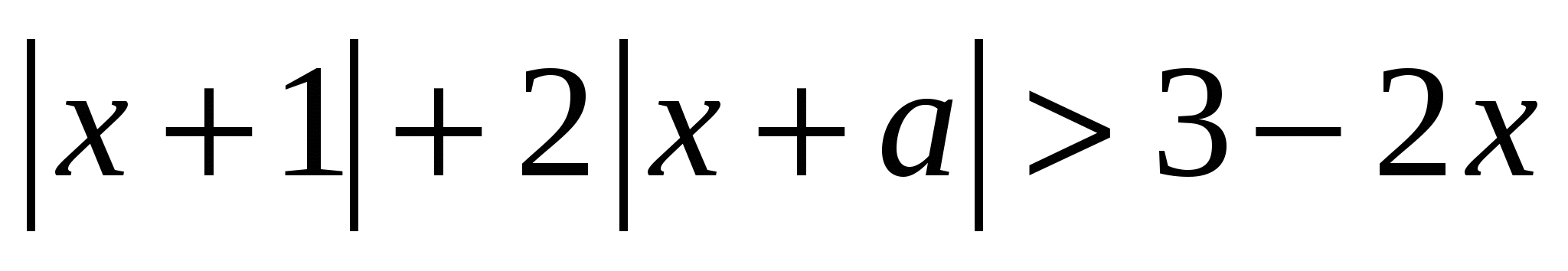 выполняется для любого выполняется для любого 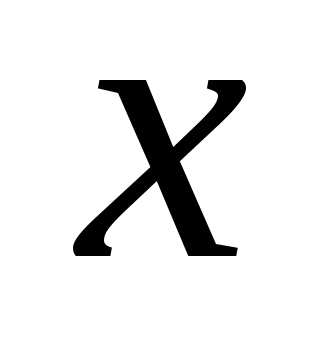 . .
|
Один из эффективных способов решения – рассмотреть разность левой и правой части, убедиться, что наименьшее значение кусочно-линейной функции (график – ломаная) с убывающим левым и возрастающим правым звеном может достигаться только в точках «стыка». На значения в них и ставим условия.
Другой хороший способ – оставить слагаемое с модулем, содержащим параметр, в одной части, а остальное перенести в другую. После строим графики обеих частей. Придется подвигать «галочку».
Полезно решить задачу двумя способами.
|
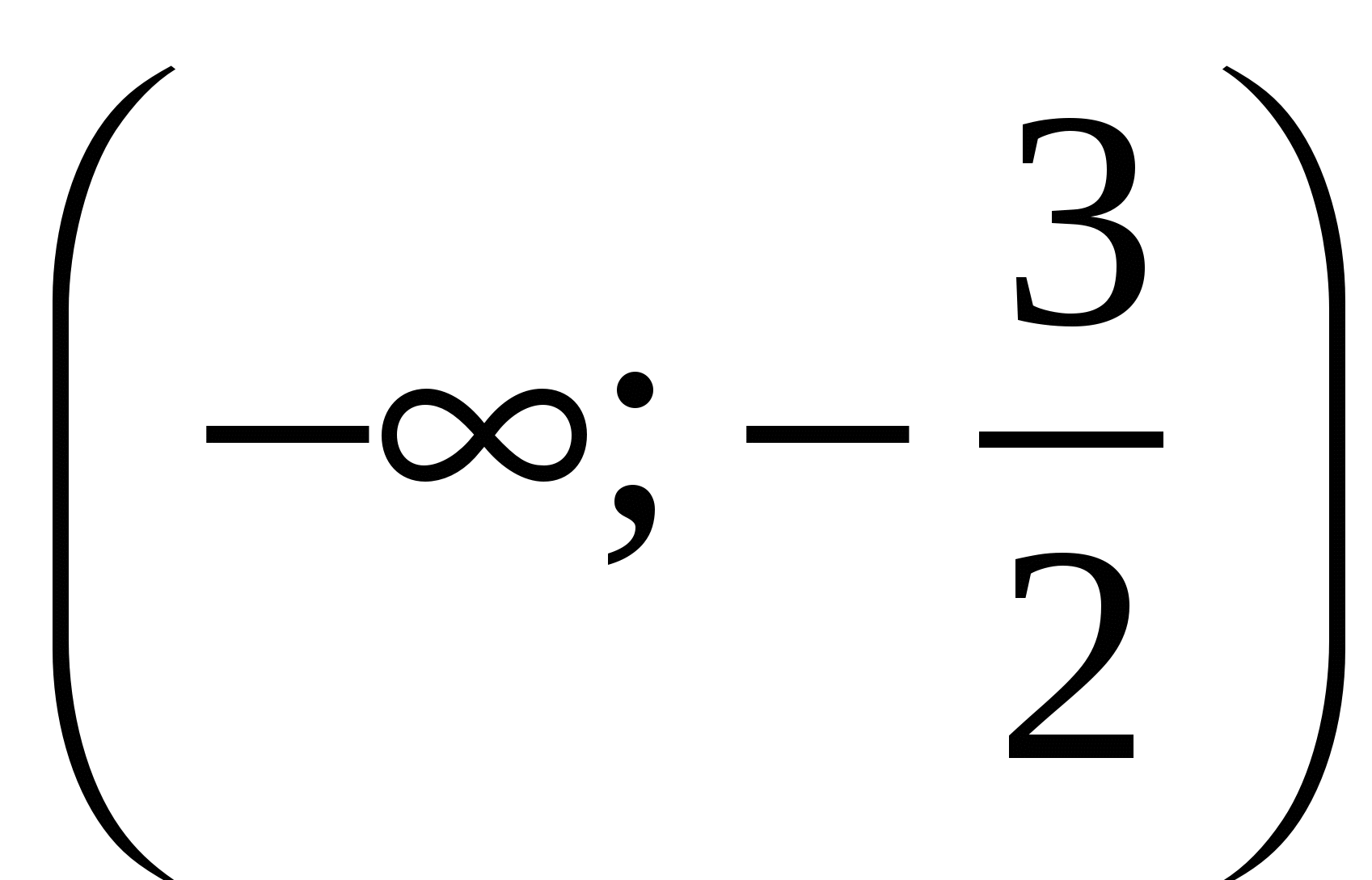
|
Найдите все значения параметра a, при которых система уравнений 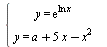 имеет два решения. имеет два решения.
|
Не забываем ограничение на переменную! Для этого дана такая первая строка в системе. Потом строим график в осях переменная-параметр. Списываем с чертежа ответ!
|
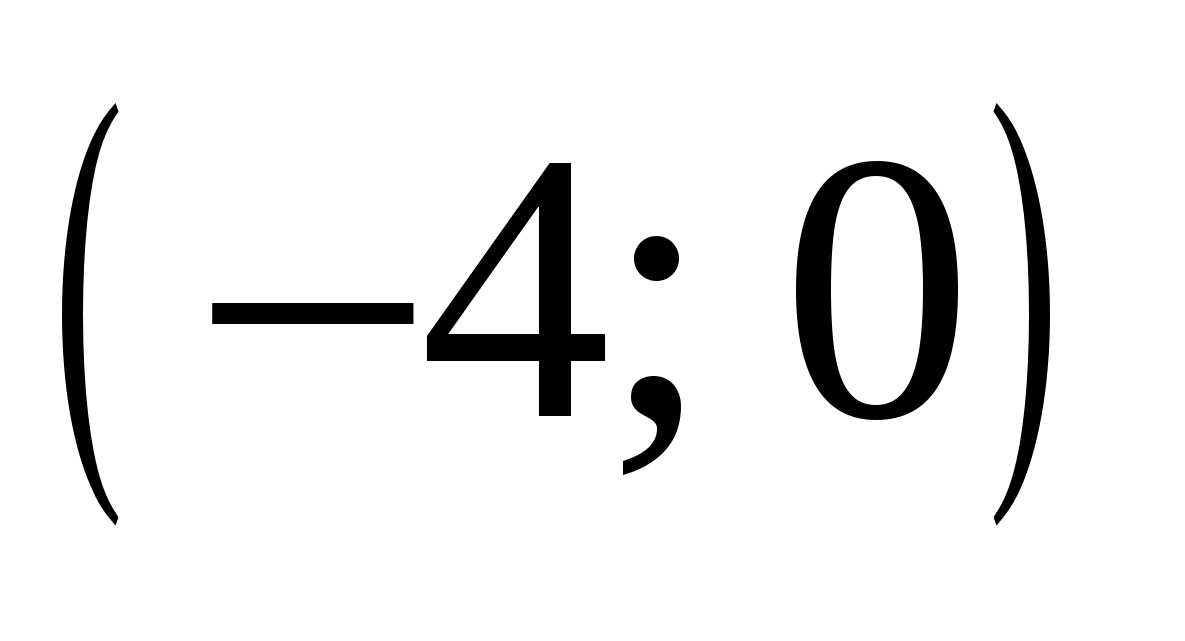
|
Найдите все значения параметра а, при каждом из которых система уравнений 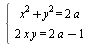 имеет ровно два решения. имеет ровно два решения.
|
Одно из уравнений системы заменяем на разность уравнений, после чего параметр остается лишь в одной строке. Работаем с «пульсирующей окружностью».
|
|
Блок 2. (задания уровня ЕГЭ)
|
Найдите все значения  , при каждом из которых уравнение , при каждом из которых уравнение 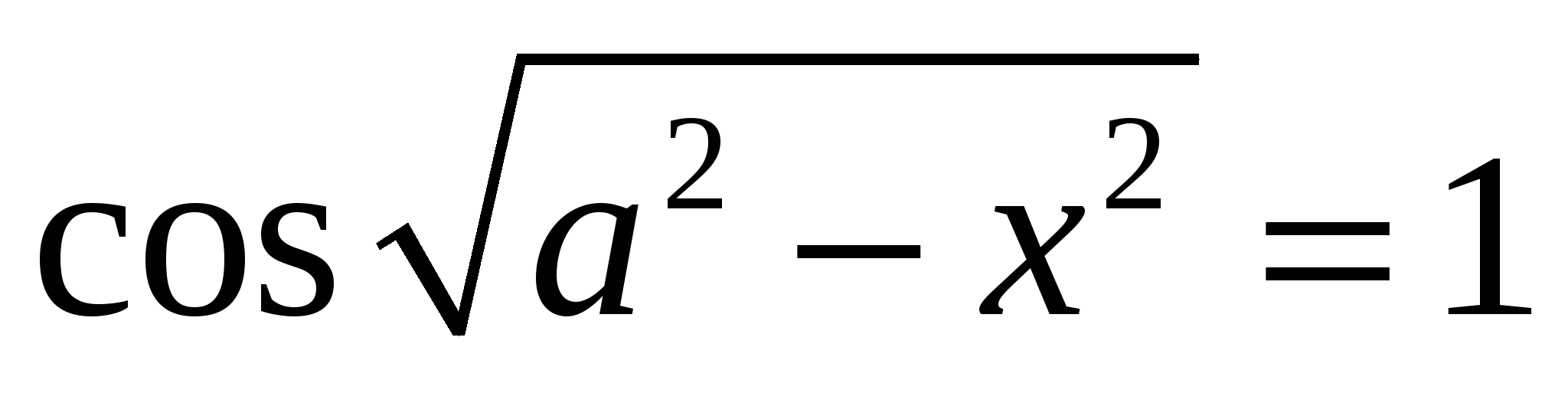 имеет ровно 8 решений. имеет ровно 8 решений.
|
Наиболее разумным представляется решение простейшего тригонометрического уравнения и построение графиков обеих частей полученной серии уравнений в системе координат хОу, далее ставим условие на количество горизонтальных прямых, которые должны пересекаться «пульсирующей» полуокружностью радиуса  . Какую по счету прямую надо пересечь, а до какой полуокружность «не дотягивается». . Какую по счету прямую надо пересечь, а до какой полуокружность «не дотягивается».
Возможно и алгебраическое решение, но оно дольше.
|
|
Найдите все значения параметра b , при каждом из которых корни уравнения 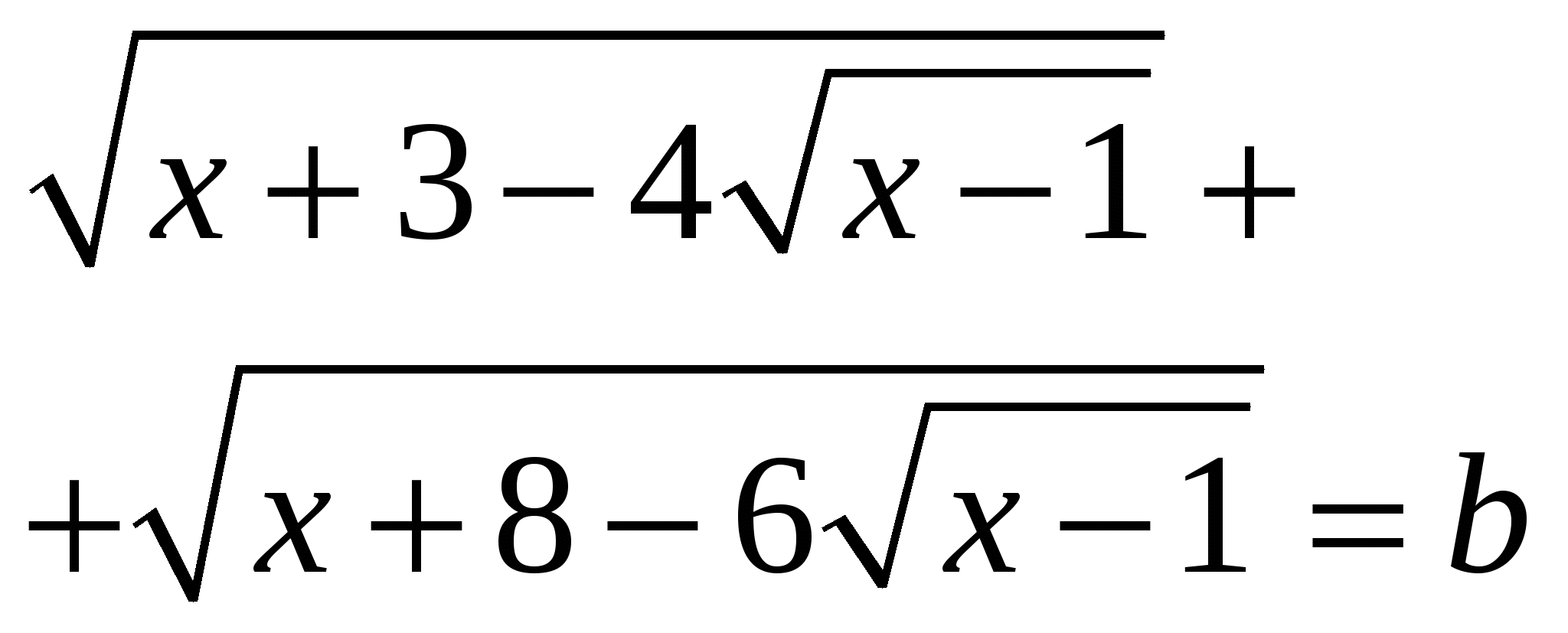 существуют и принадлежат отрезку |2;17]. существуют и принадлежат отрезку |2;17].
|
Первым действием заменяем переменную. Важно, что одно решение по переменной 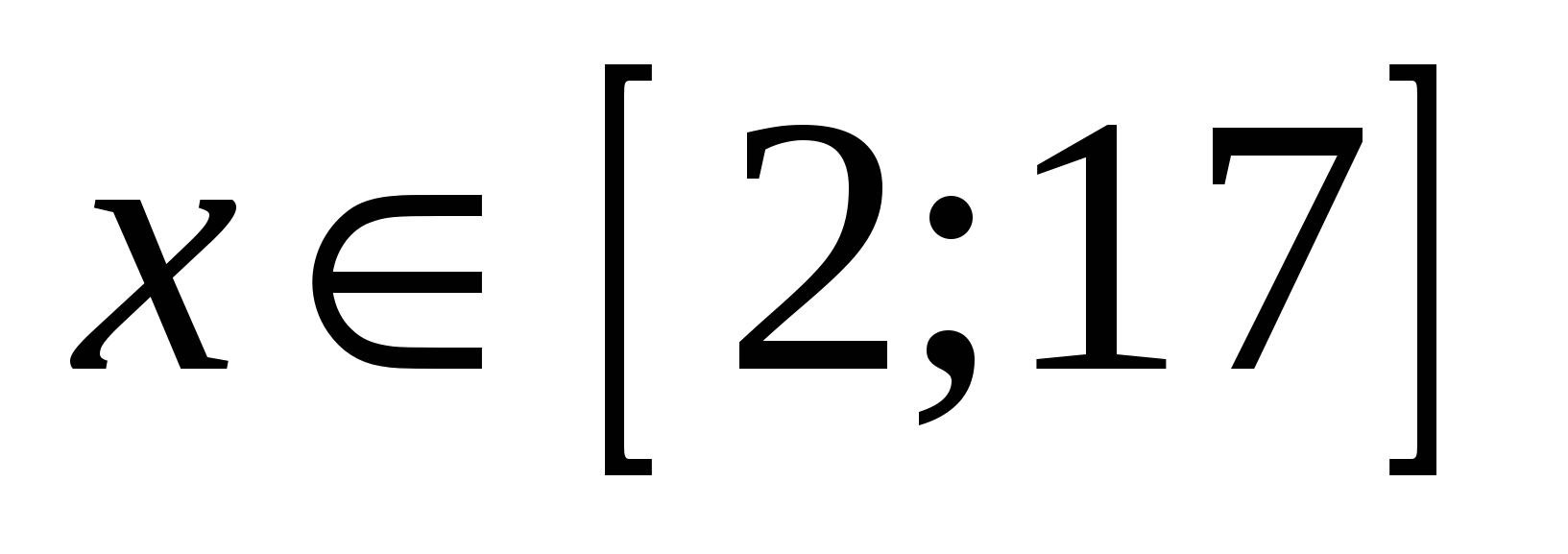 исходного уравнения соответствует одному решению нового уравнения с модулями относительно новой переменной исходного уравнения соответствует одному решению нового уравнения с модулями относительно новой переменной 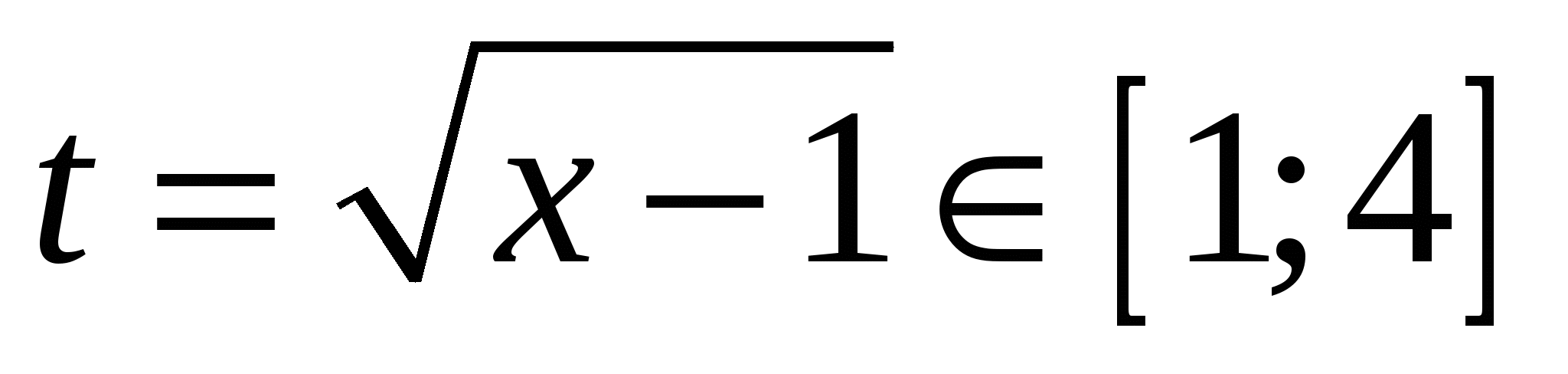 . Далее строим график в осях . Далее строим график в осях 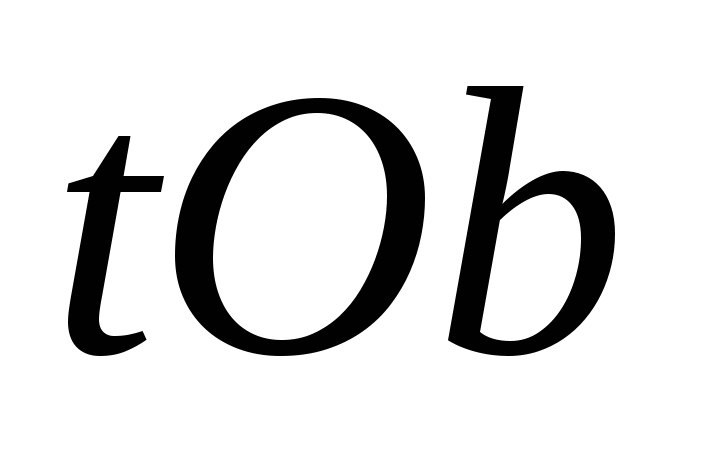 , и мы готовы дать ответ на любой вопрос о количестве и качестве решений исходного уравнения. , и мы готовы дать ответ на любой вопрос о количестве и качестве решений исходного уравнения.
|
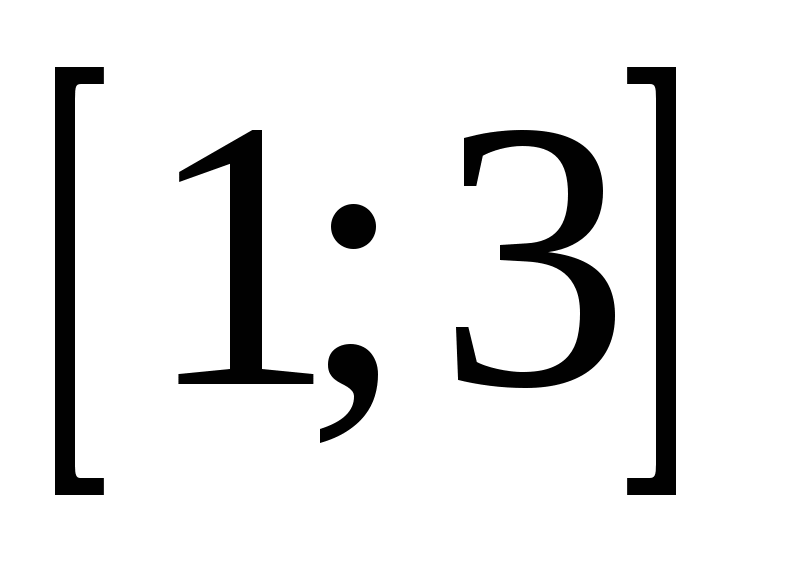
|
Найдите все значения а, при каждом из которых система 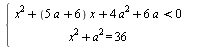
имеет решения.
|
Работаем в осях переменная-параметр. Разложив левую часть верхней строки на множители, видим два вертикальных кгла без границ, которые высекают на окружности две дуги (тоже без границ). Найдя соответствующие концам дуг значения параметра, пишем ответ.
|
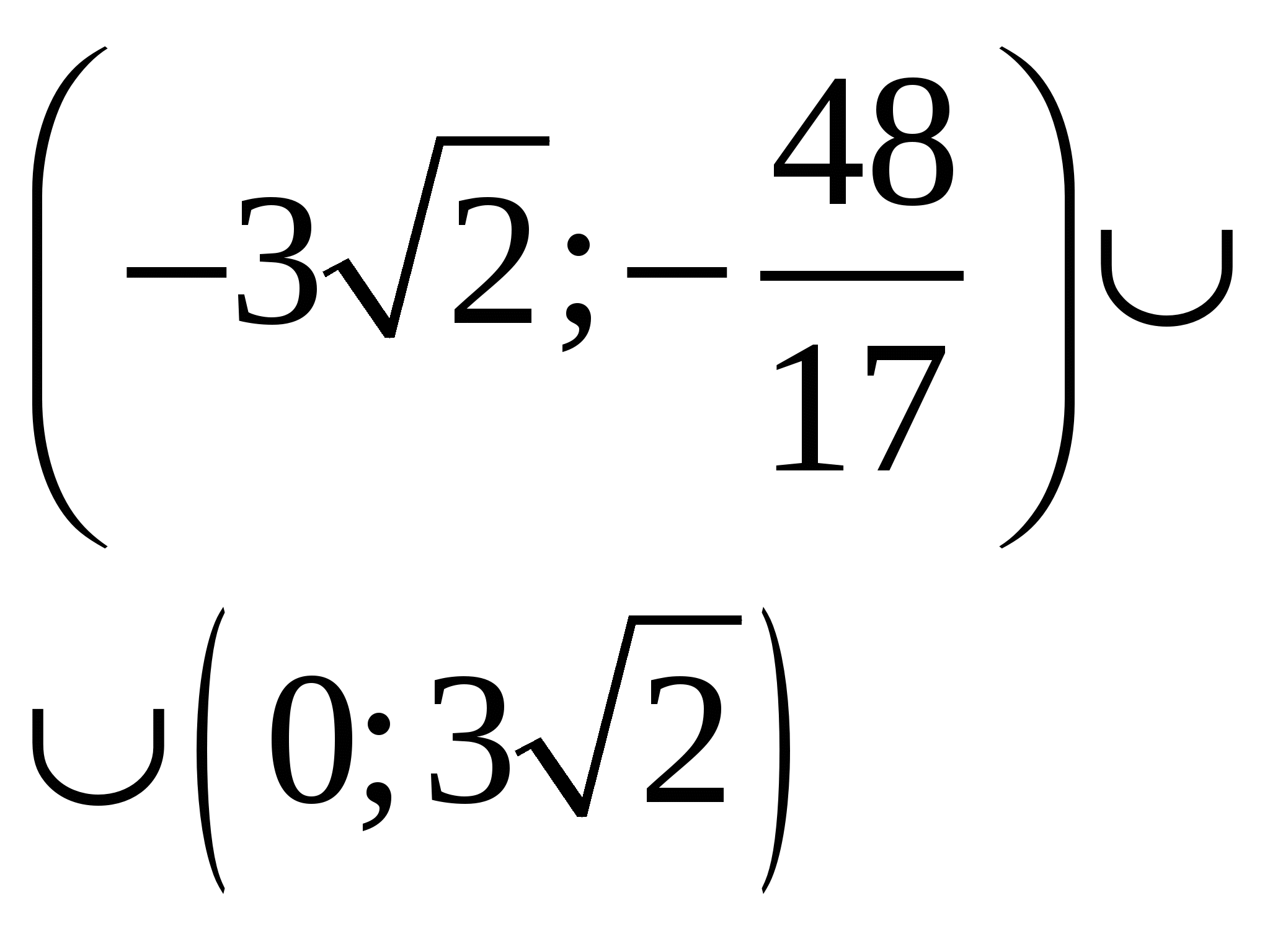
|
Найдите все значения а, при каждом из которых множество значений функции 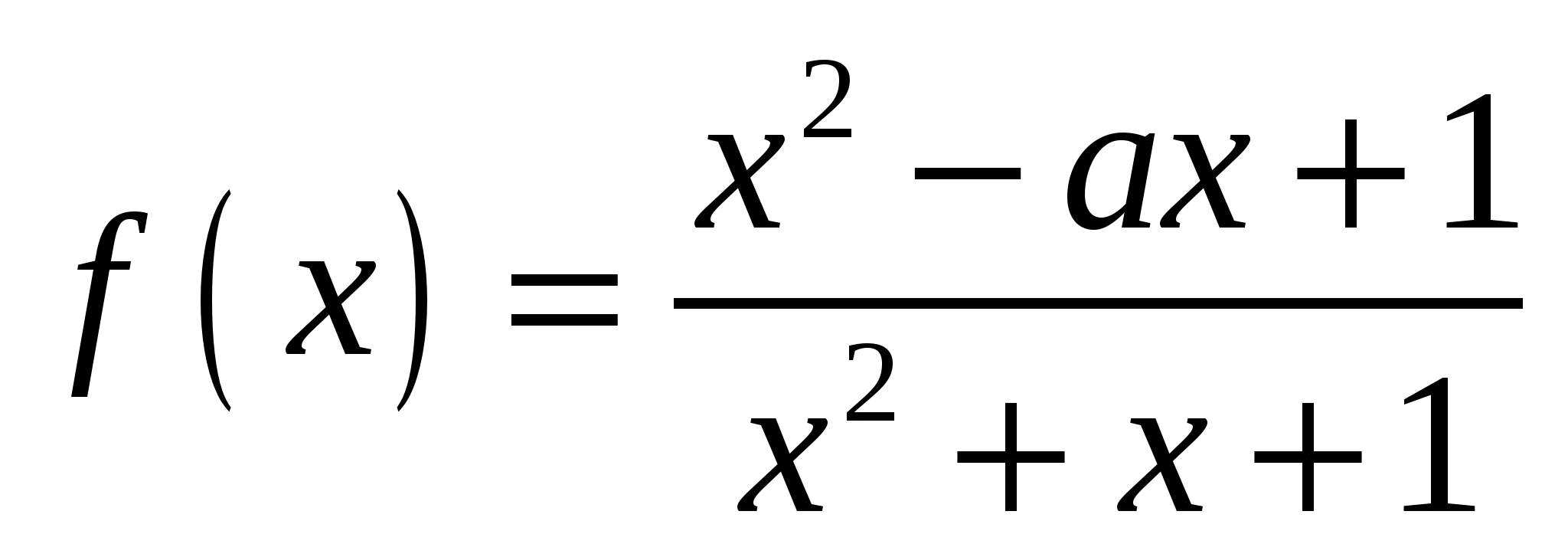 лежит в интервале лежит в интервале 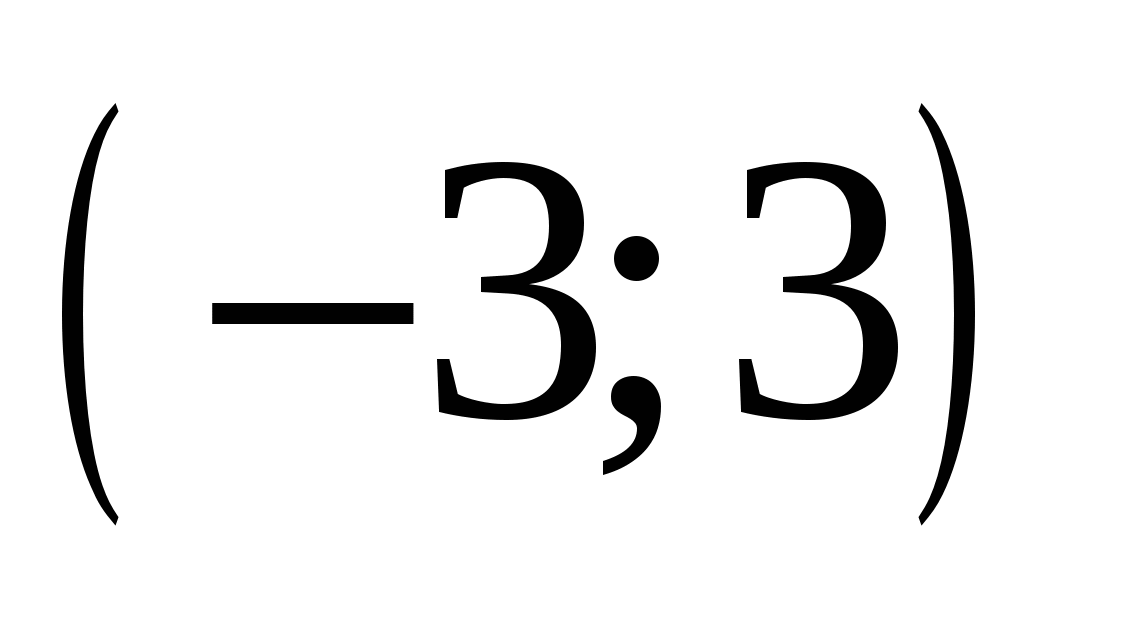 . .
|
Обращаем внимание на то, что знаменатель положителен при всех 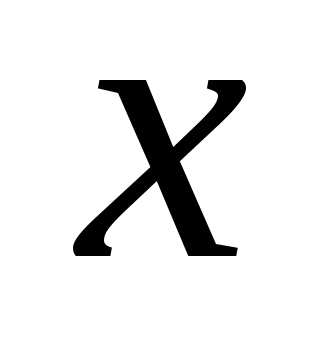 , то есть на него можно домножать. Получаем систему двух неравенств, каждое из которых (!) должно выполняться при всех значениях переменной. Работа только с дискриминантами. Дело техники. , то есть на него можно домножать. Получаем систему двух неравенств, каждое из которых (!) должно выполняться при всех значениях переменной. Работа только с дискриминантами. Дело техники.
|
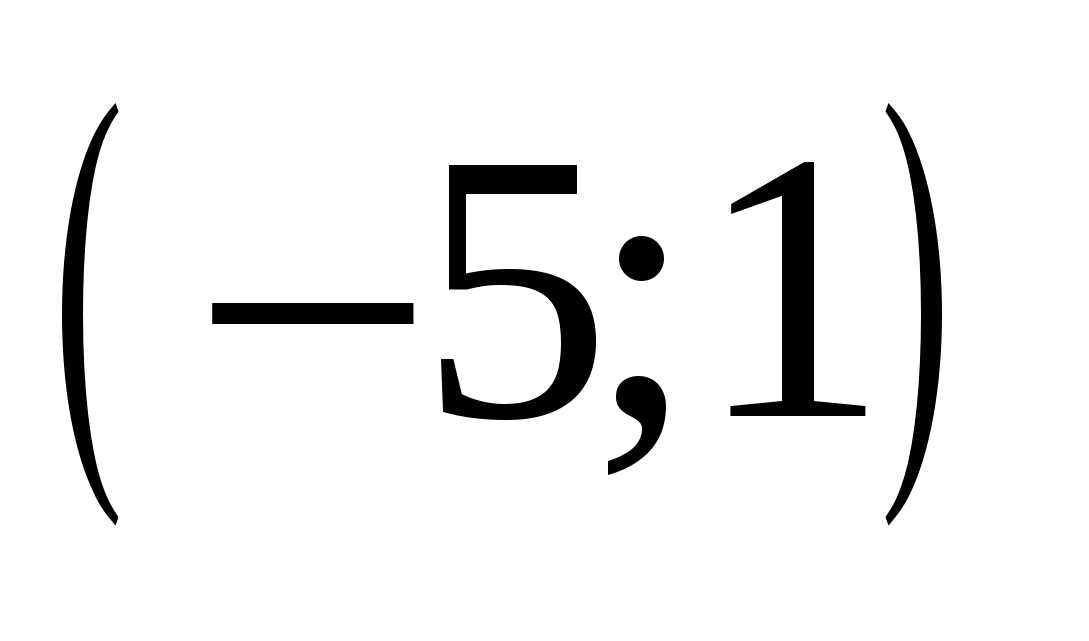
|
При каких значениях параметра С уравнение 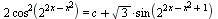 имеет решения ? имеет решения ?
|
Очень хорошая задача на множество значений сложной(!) функции. Попутно надо увидеть возможность введения вспомогательного аргумента, а далее придется найти все значения внутренней (показательной с квадратичным аргументом) функции и определить взаимное расположение чисел на тригонометрической окружности.
|
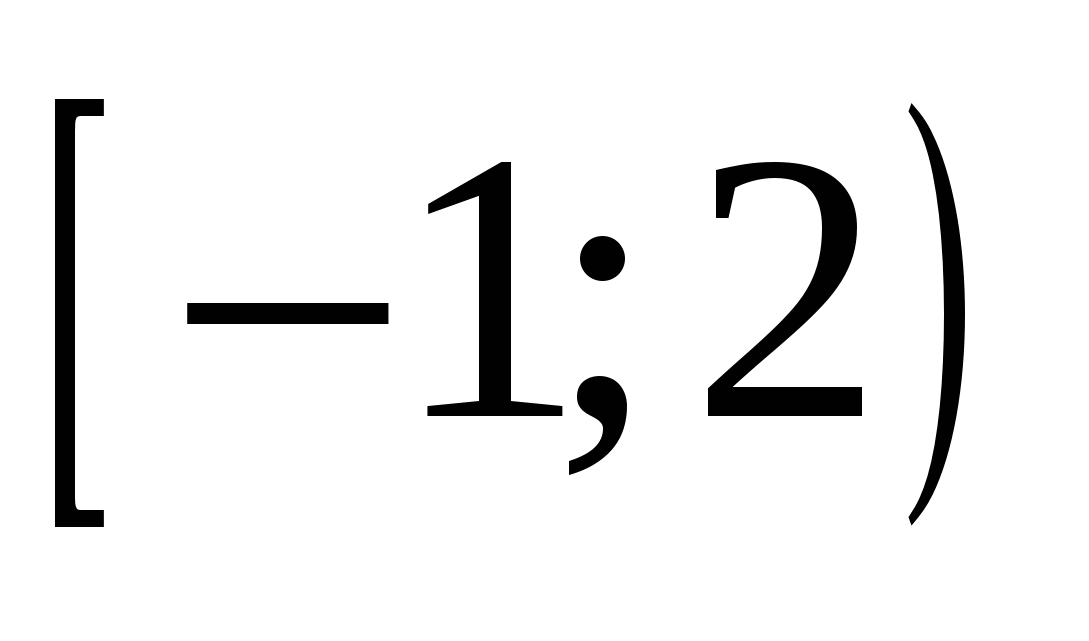
|
Найдите все значения а, при которых система 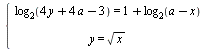 имеет решения. имеет решения.
|
Проанализировав связь количества решений исходной системы и уравнения относительно 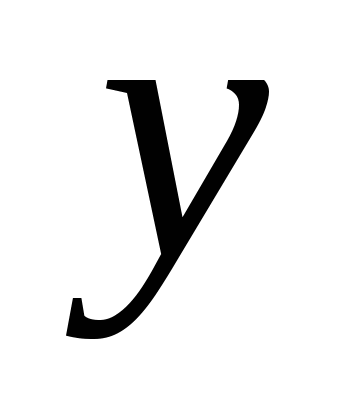 с параметром с параметром  , изображаем график в осях , изображаем график в осях 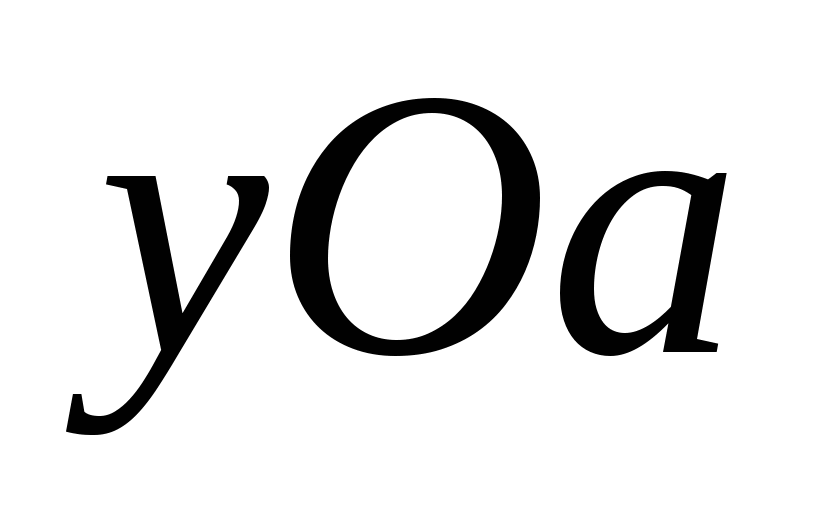 . Учитывая все нужные ограничения, получаем ответ. . Учитывая все нужные ограничения, получаем ответ.
|
|
Найдите все положительные значения а, при каждом из которых система 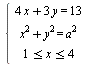 имеет единственное решение. имеет единственное решение.
|
Задача сводится к исследованию отрезка квадратичной функции. Некоторое количество вычислений…
|
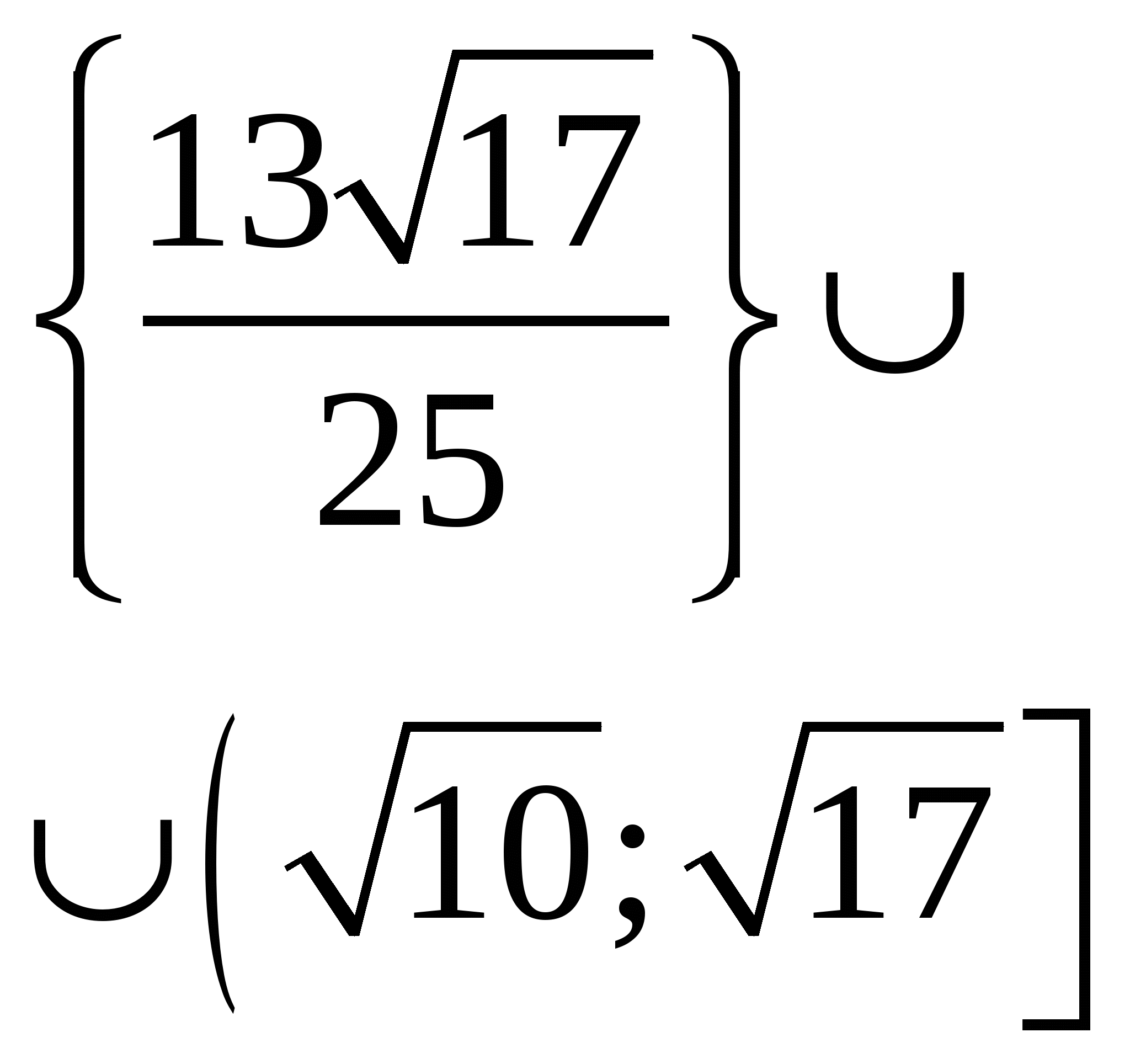
|
Найдите все значения а и b такие, что система 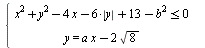 имеет ровно 2 различных решения. имеет ровно 2 различных решения.
|
Анализ геометрической ситуации. Приходим к выводу, что окружности (модуль!) не должны сливаться, а прямая должна касаться обеих окружностей. Геометрия помогает получить ответ.
|
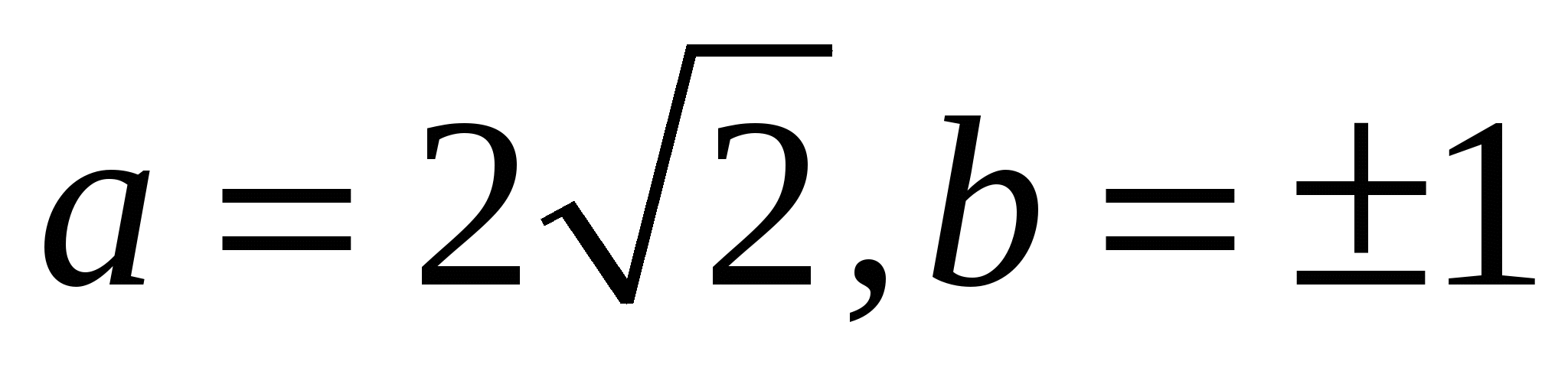
|
Найдите все значения a, при каждом из которых функция 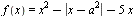 имеет более двух точек экстремума. имеет более двух точек экстремума.
|
Конструируем кусочно- квадратичную функцию так, чтобы выполнялось условие задачи. Смотрим, где должны быть вершины частей.
|
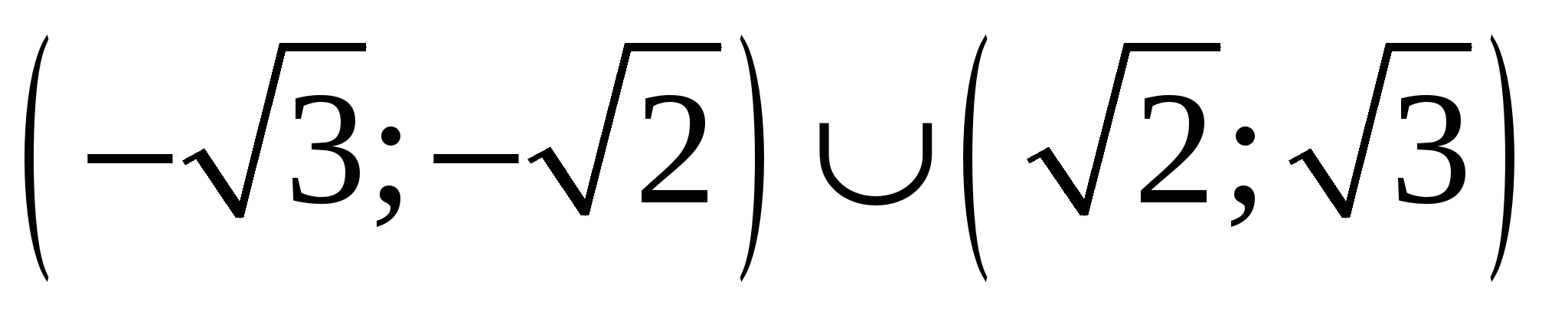
|
Найдите все значения a, при каждом из которых наименьшее значение функции 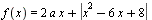 меньше 1. меньше 1.
|
Красивое логическое действие: наименьшее значение функции (если оно есть) меньше числа тогда и только тогда, когда хоть какое-нибудь значение меньше этого числа. Наибольшее значение меньше числа, когда все значения меньше. Наименьшее больше – когда все больше. Наибольшее больше- когда хоть какое-нибудь больше.
Далее строим неподвижный график, и. вращая прямую вокруг фиксированной точки, добиваемся выполнения поставленного условия.
|
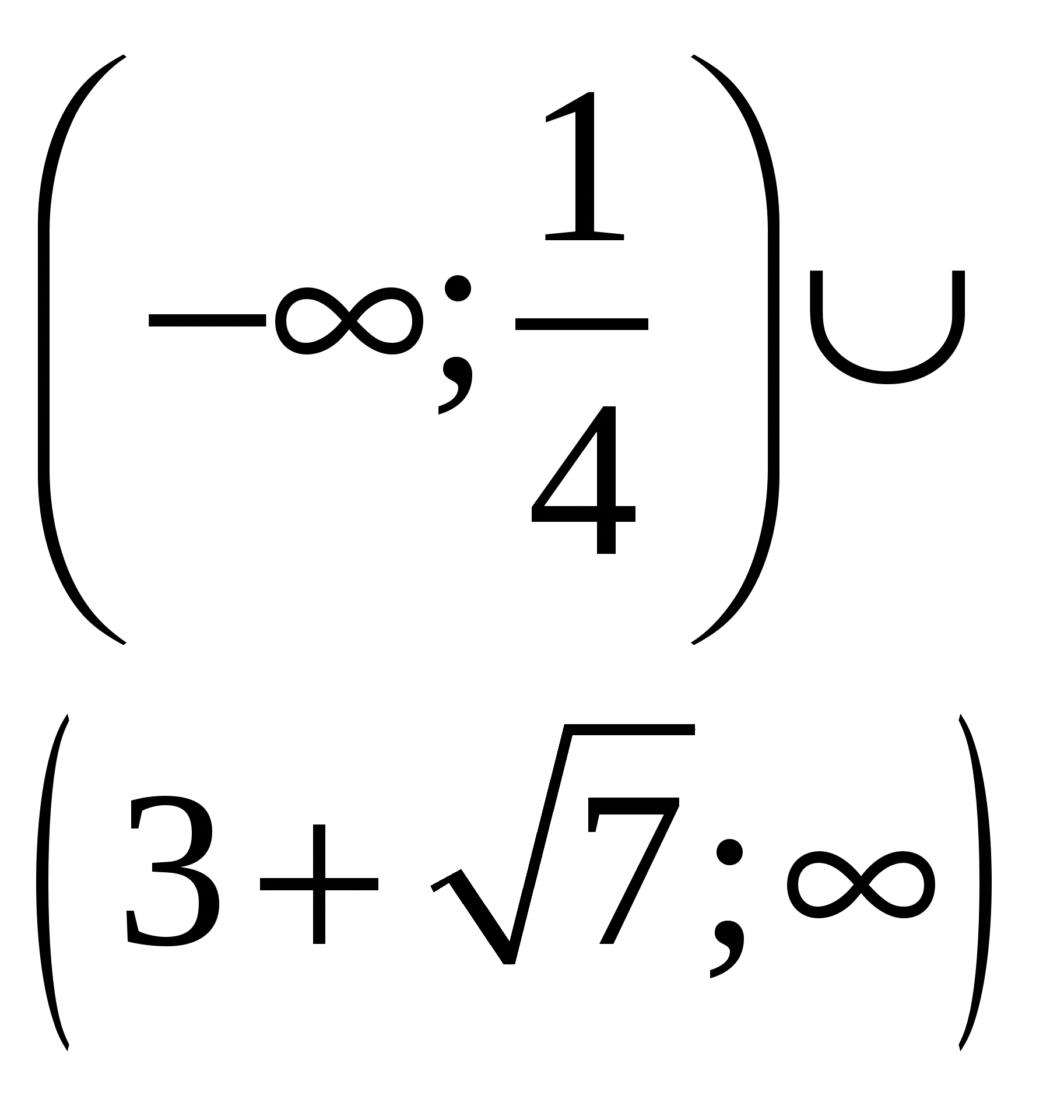
|
Найдите все значения a, при каждом из которых все решения неравенства 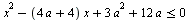 удовлетворяют неравенству удовлетворяют неравенству 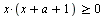 . .
|
Разложение на множители, построение графиков неравенств методом областей и анализ взаимного расположения графиков. Найдя соответствующие границам значения параметра, пишем ответ.
|
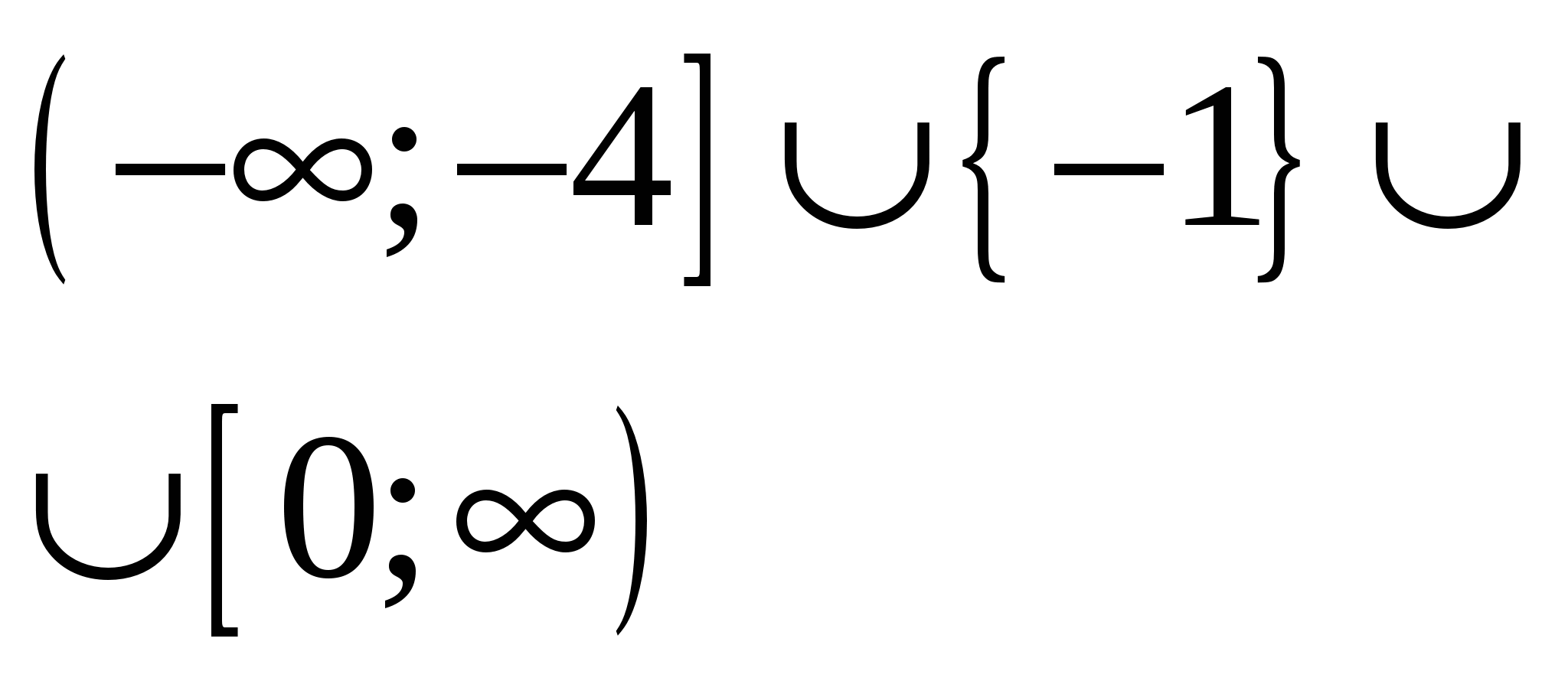
|
Найдите наибольшее значение параметра a, при котором функция 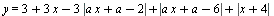 является неубывающей на всей числовой прямой. является неубывающей на всей числовой прямой.
|
Во-первых, ищем положительное значение параметра. Если положительные есть, то наибольшее – среди них! Далее удобно взять не переменную 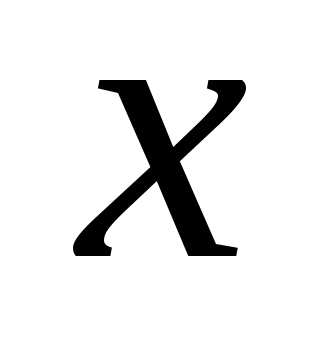 , а переменную , а переменную 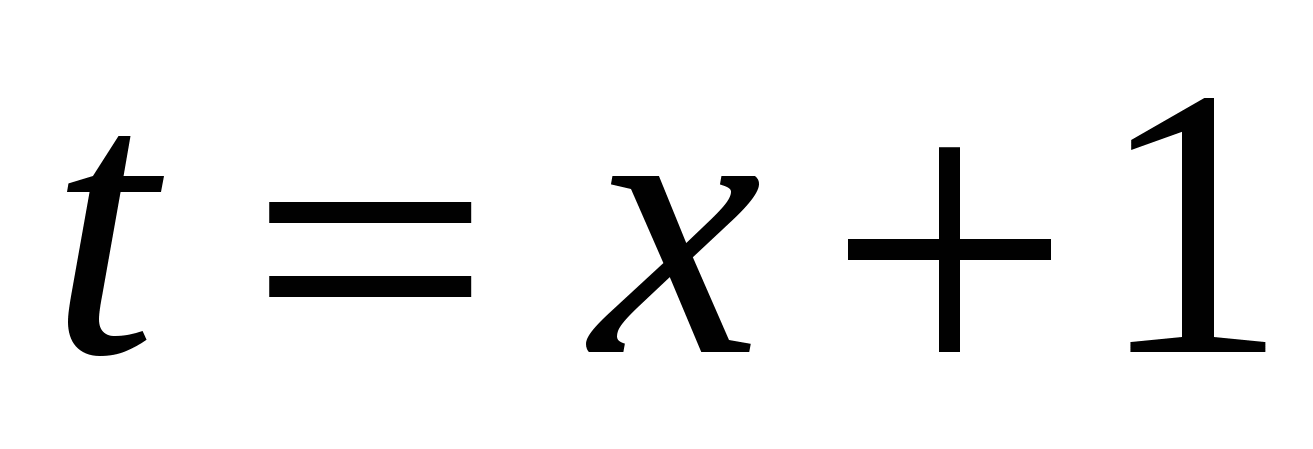 . Монотонность от этого не меняется. График – ломаная. Найдя пределы на бесконечности, определяем взаимное расположение экстремумов. . Монотонность от этого не меняется. График – ломаная. Найдя пределы на бесконечности, определяем взаимное расположение экстремумов.
|
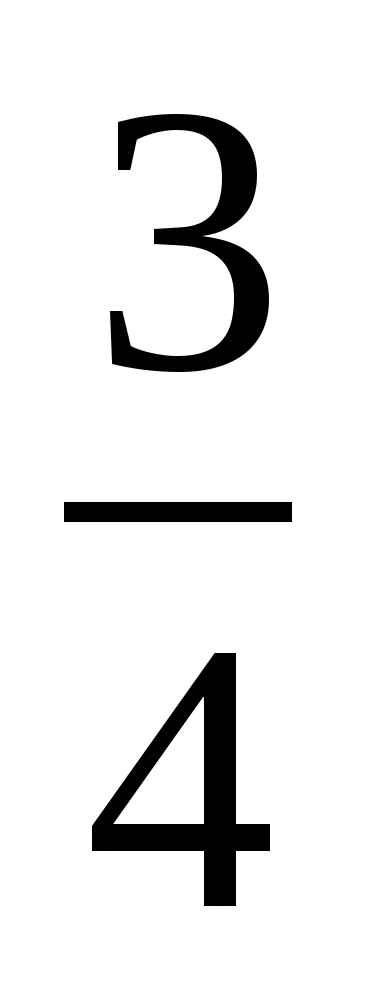
|
Найдите все значения a, при каждом из которых уравнение 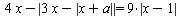 имеет хотя бы один корень. имеет хотя бы один корень.
|
Нужно понимать, что график функции в левой части представляет собой ломаную, то есть функция непрерывна; пределы на бесконечности равны 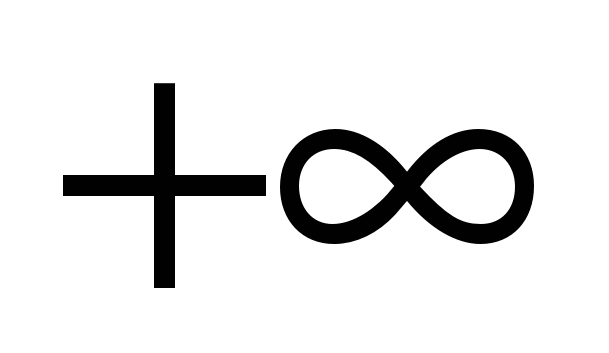 . Проверьте коэффициенты при . Проверьте коэффициенты при 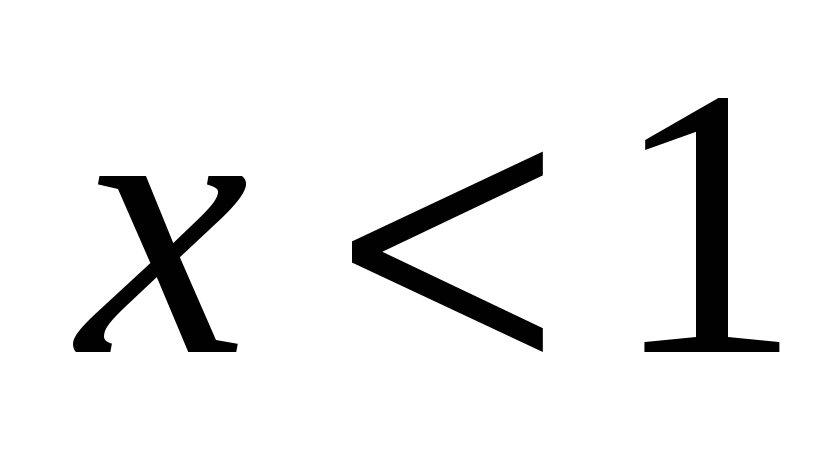 и при и при 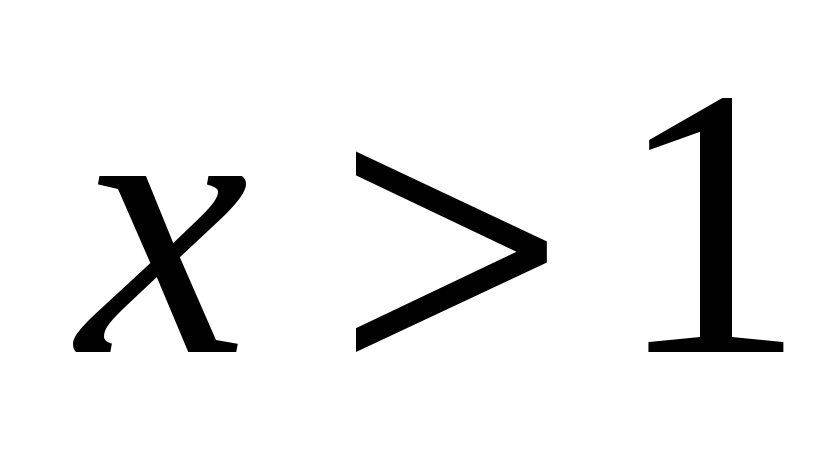 и сделайте вывод об экстремуме, дающем наименьшее значение. Далее решение задачи даст техника решения неравенств с модулями. и сделайте вывод об экстремуме, дающем наименьшее значение. Далее решение задачи даст техника решения неравенств с модулями.
Возможно другое решение – бесхитростное построение графика в осях переменная-параметр, но оно требует значительно большего времени. Довольно трудоемко, но надежно. Можно даже… сам график не строить, а указать на его особенности и просчитать значения в точках «стыка».
|
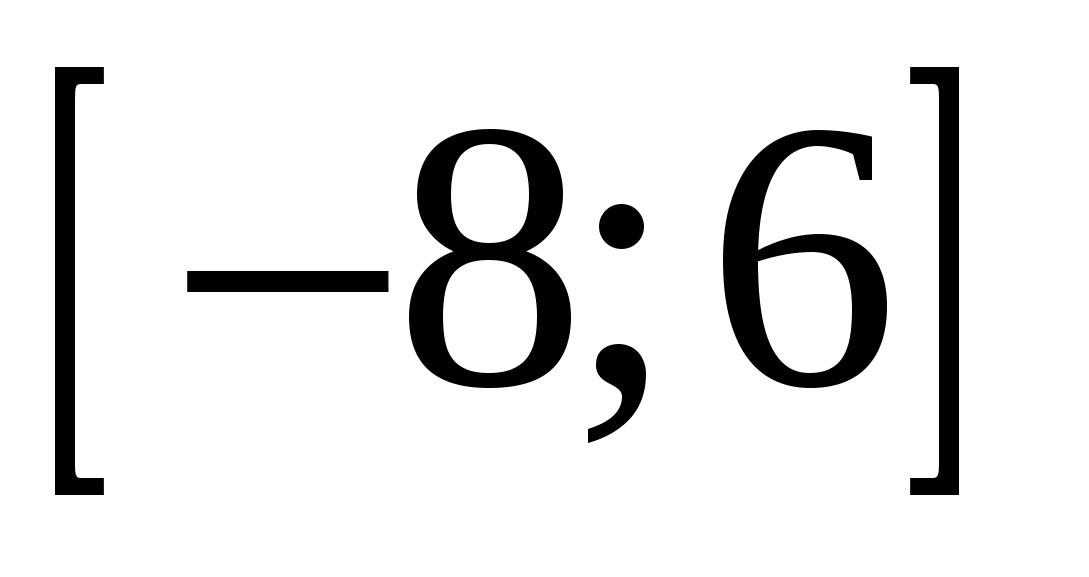
|
Найдите все значения параметра а, при каждом из которых система 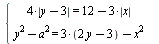 имеет ровно 4 решения. имеет ровно 4 решения.
|
Элементарные навыки построения графиков с модулями, плюс исследование «пульсирующей окружности». Да, еще умение вычислять высоту прямоугольного треугольника.
|
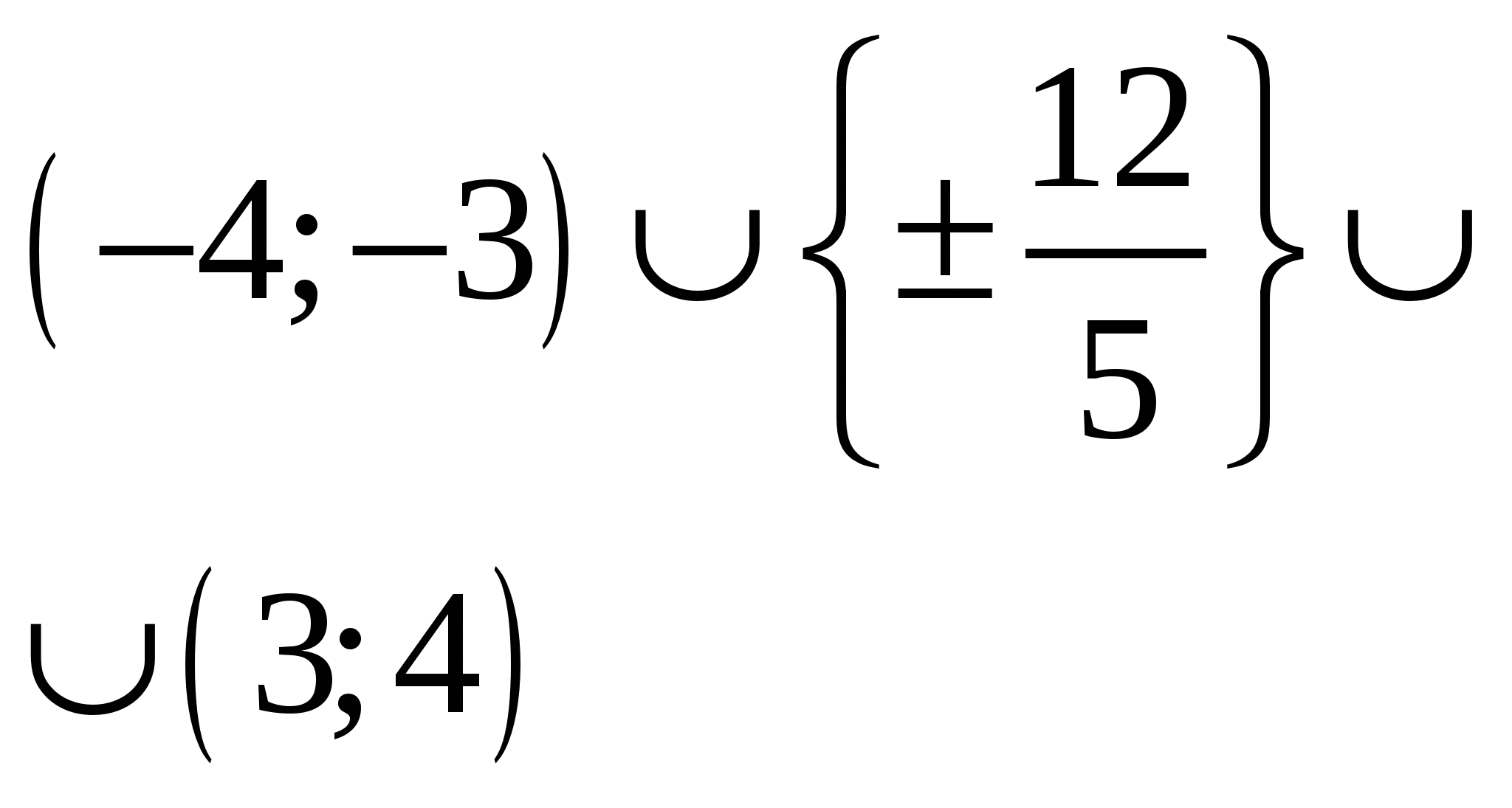
|
Найдите все значения параметра а, при которых система 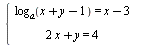 имеет единственное решение. имеет единственное решение.
|
Придется аккуратно решить классический вопрос о единственности решения уравнения с помощью исследования графика функции, связанной с логарифмами. Применяем математический анализ.
|
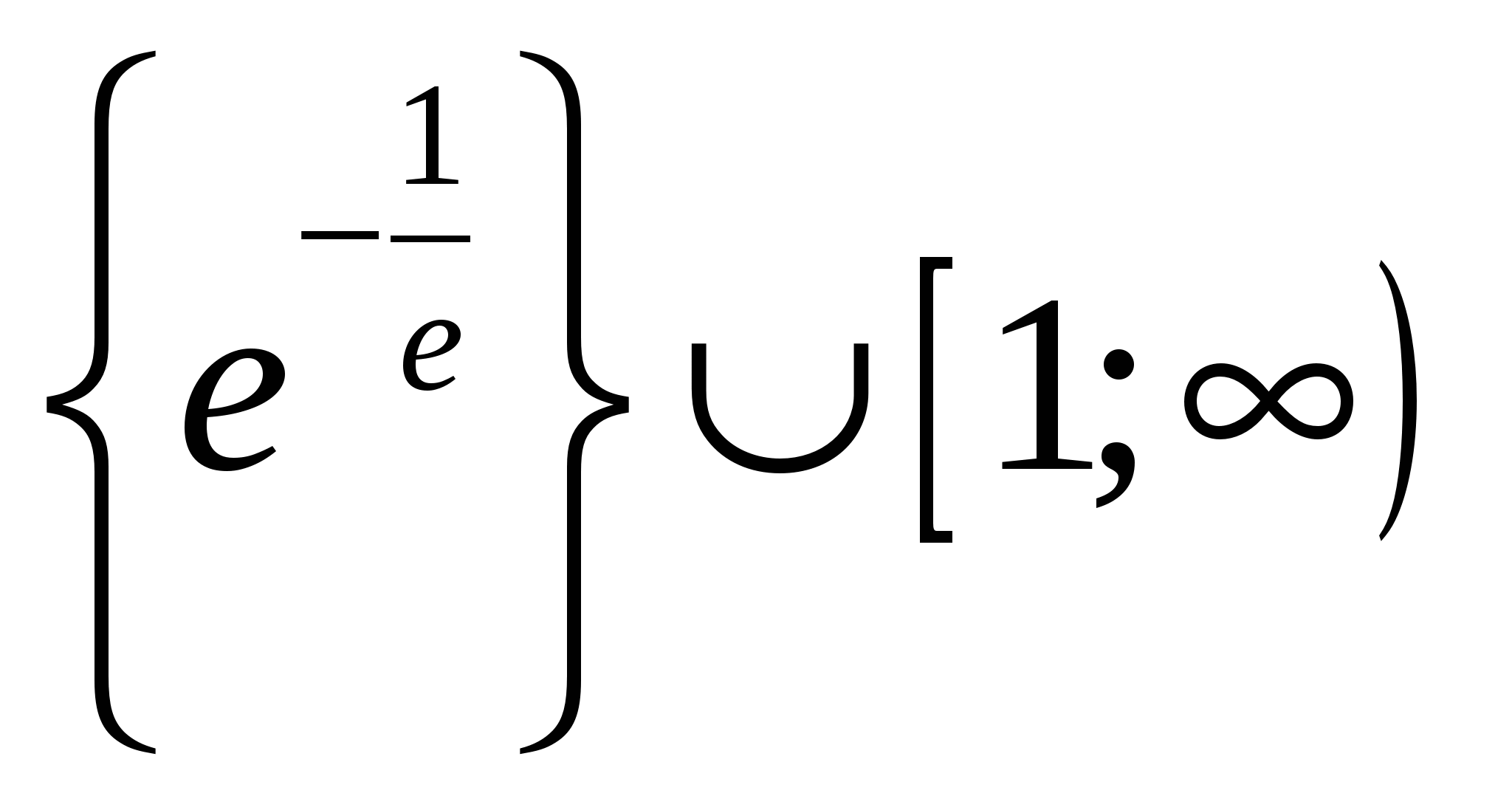
|
Для каждого значения 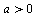 найдите уравнения всех прямых, проходящих через начало координат и имеющих ровно две общие точки с графиком функции найдите уравнения всех прямых, проходящих через начало координат и имеющих ровно две общие точки с графиком функции 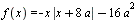 . .
|
График, зависящий от параметра, правда, его форма определена четко. Далее вращаем прямую вокруг начала координат. Попутно придется найти касательную. Аккуратнее с количеством пересечений прямой с ветвью параболы! Здесь могут быть ошибки.
|
|
Известно, что значение параметра a таково, что система уравнений  имеет единственное решение. Найдите это значение параметра a и решите систему при найденном значении параметра. имеет единственное решение. Найдите это значение параметра a и решите систему при найденном значении параметра.
|
Используется симметрия множества решений, связанная с четностью функций по 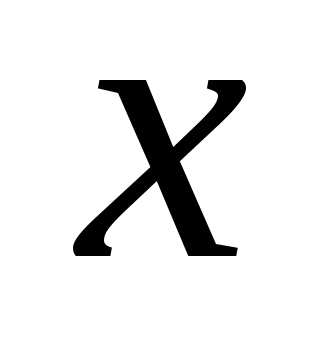 . С помощью этой симметрии получаем необходимое (но не достаточное) условие единственности решения. Далее придется проверить каждое из найденных значений параметра. . С помощью этой симметрии получаем необходимое (но не достаточное) условие единственности решения. Далее придется проверить каждое из найденных значений параметра.
|
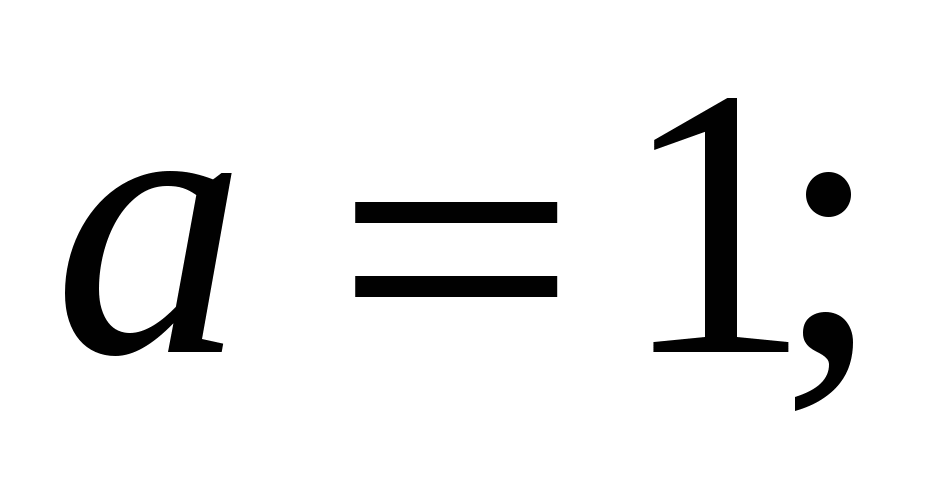 решение решение 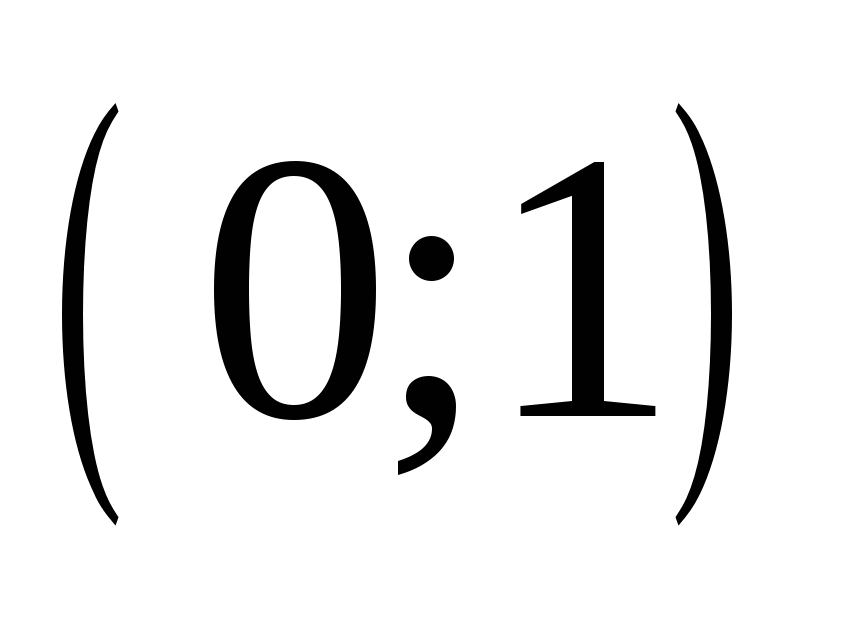
|
Определить, при каких значениях параметра b для любых значений параметра a система уравнений 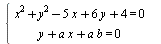 имеет ровно два различных решения ( x ; y ) . имеет ровно два различных решения ( x ; y ) .
|
Задача содержит два параметра, но очевидным образом проглядывается основной мотив: гарантировать два пересечения прямой с окружностью может только нахождение фиксированной точки прямой внутри окружности. Далее немного геометрии.
|
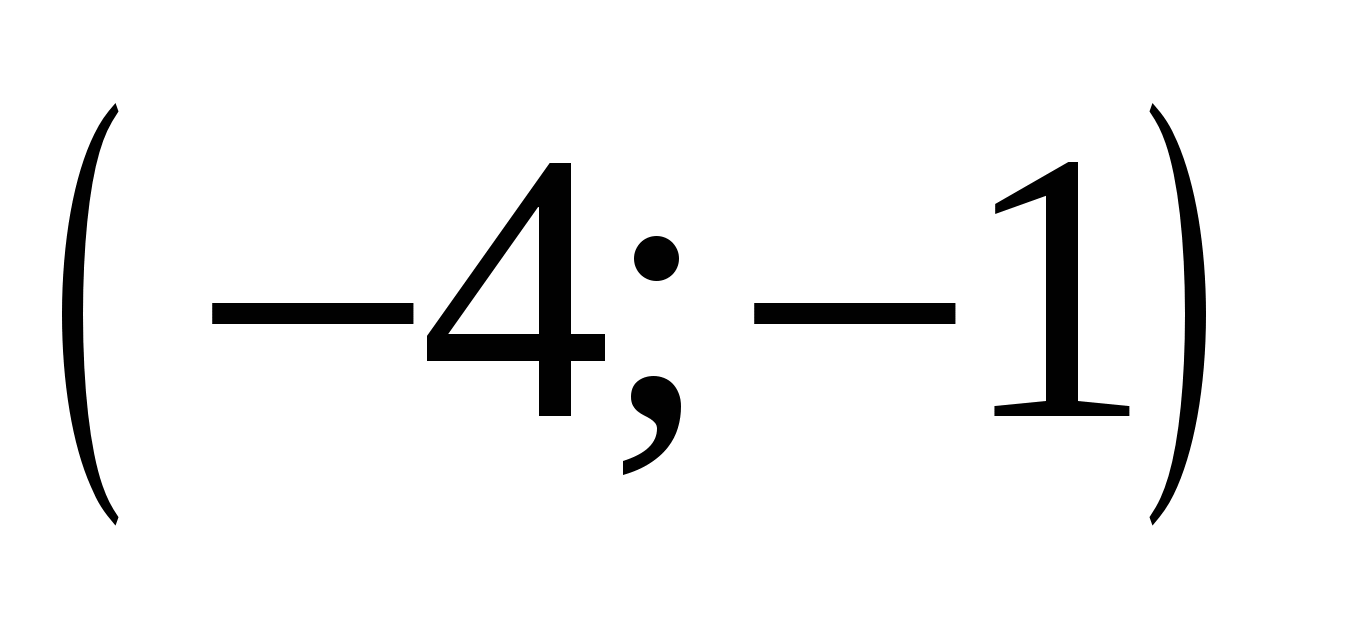
|
Найдите все значения параметра а, при которых общие решения неравенств 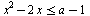 и и 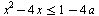 образуют на числовой оси отрезок длины единица. образуют на числовой оси отрезок длины единица.
|
Пересечение внутренних областей двух парабол с различным направлением ветвей может заключать горизонтальный отрезок длины 1 в трех разных случаях…. Вот их-то и надо внимательно рассмотреть. Придется порешать неболшие иррациональные уравнения и посравнивать числа, содержащие иррациональности.
|
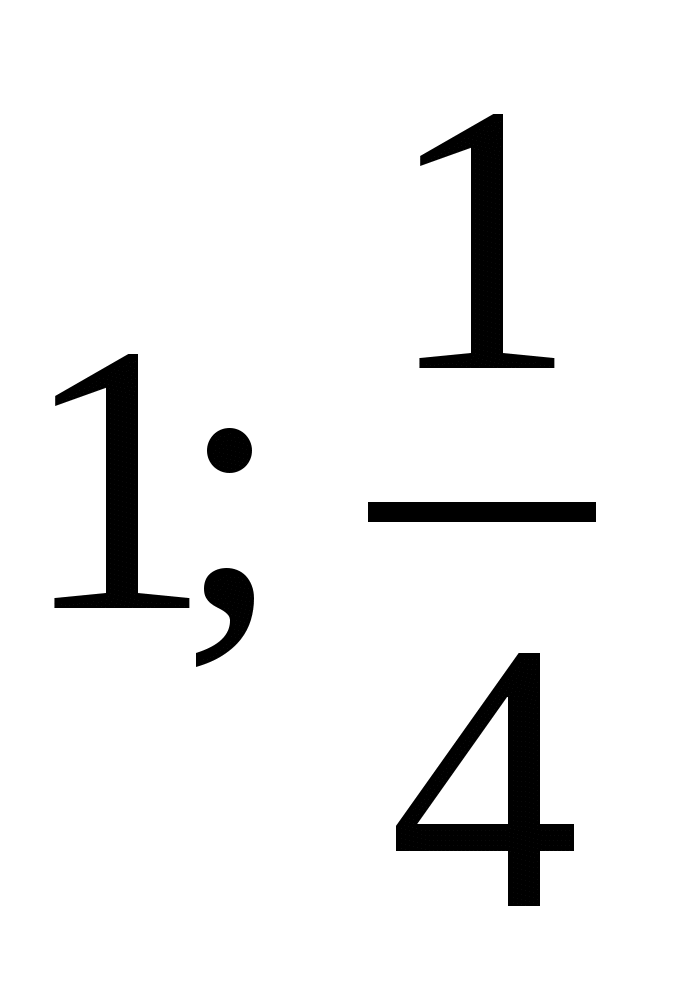
|
Найдите все значения а, при каждом из которых любая прямая, перпендикулярная оси ординат, имеет нечетное число общих точек с графиком функции 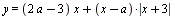 . .
|
Анализ монотонности кусочно-квадратичной функции сводится к локализации вершин парабол.
|
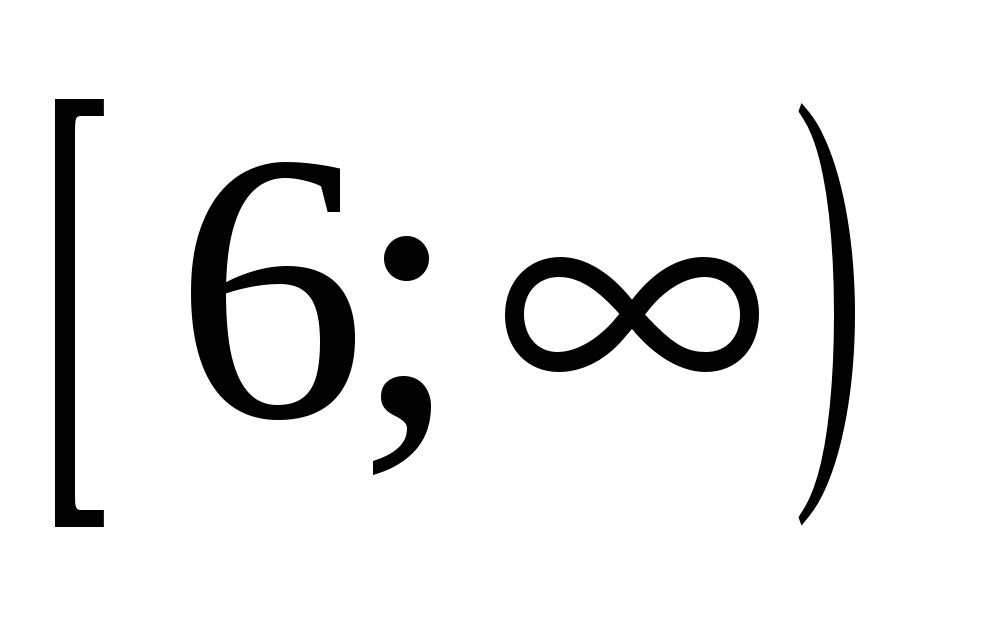
|
Найдите все значения а , при каждом из которых существует прямая, перпендикулярная оси ординат и имеющая четное число общих точек с графиком функции 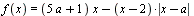 . .
|
Задача аналогична предыдущей, но немного поменяли вопрос и поставили ограничение, связанное с параметром. Решается так же. Нужен хотя бы один экстремум.
|
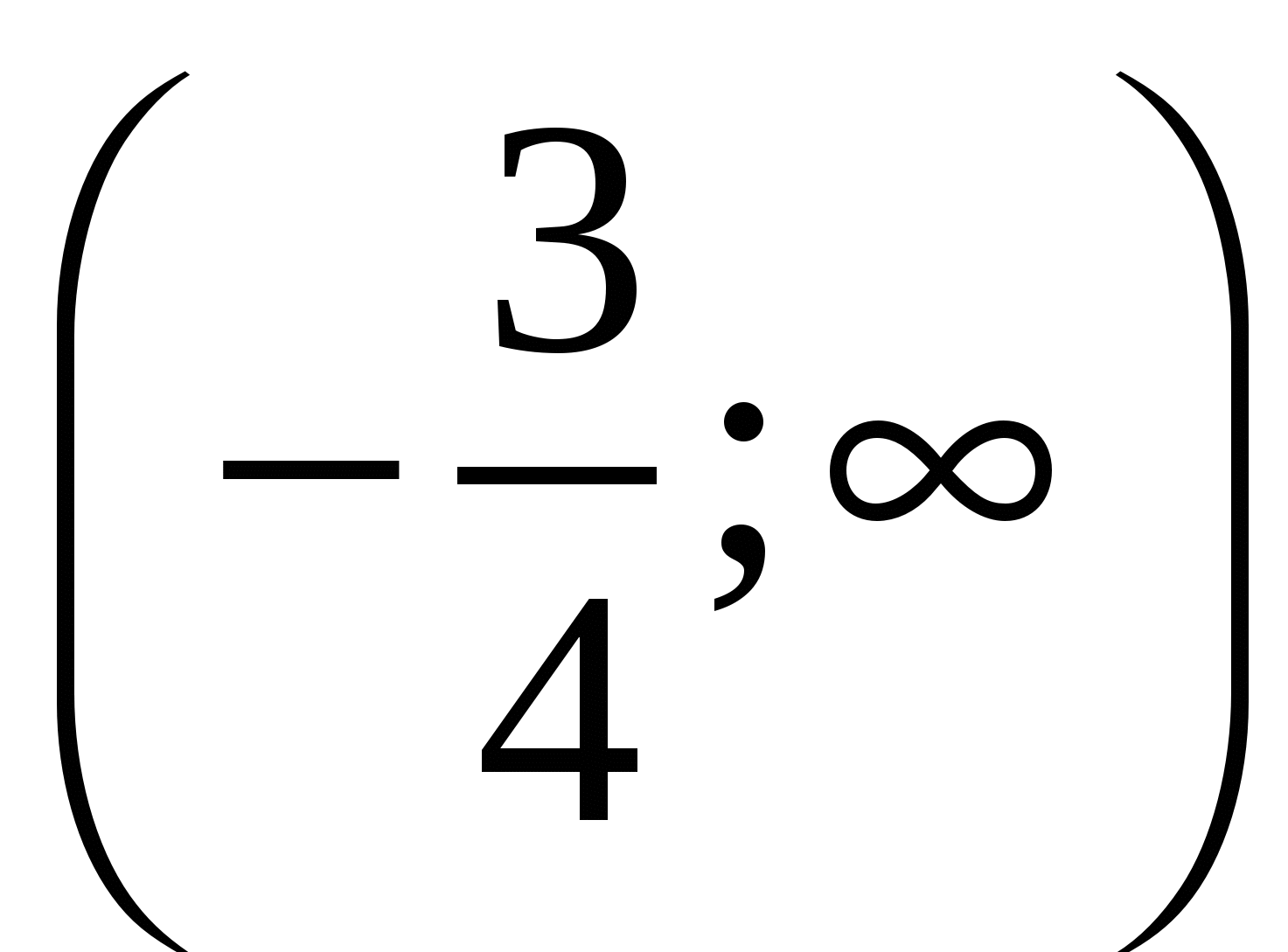
|
Найти все значения а, для которых при каждом х из промежутка [−2;−1) значение выражения 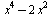 не равно значению выражения не равно значению выражения 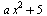 . .
|
Замена переменной и расположение корней квадратного трехчлена. Четыре случая расположения параболы. Внимательно! Реализуются два.
|
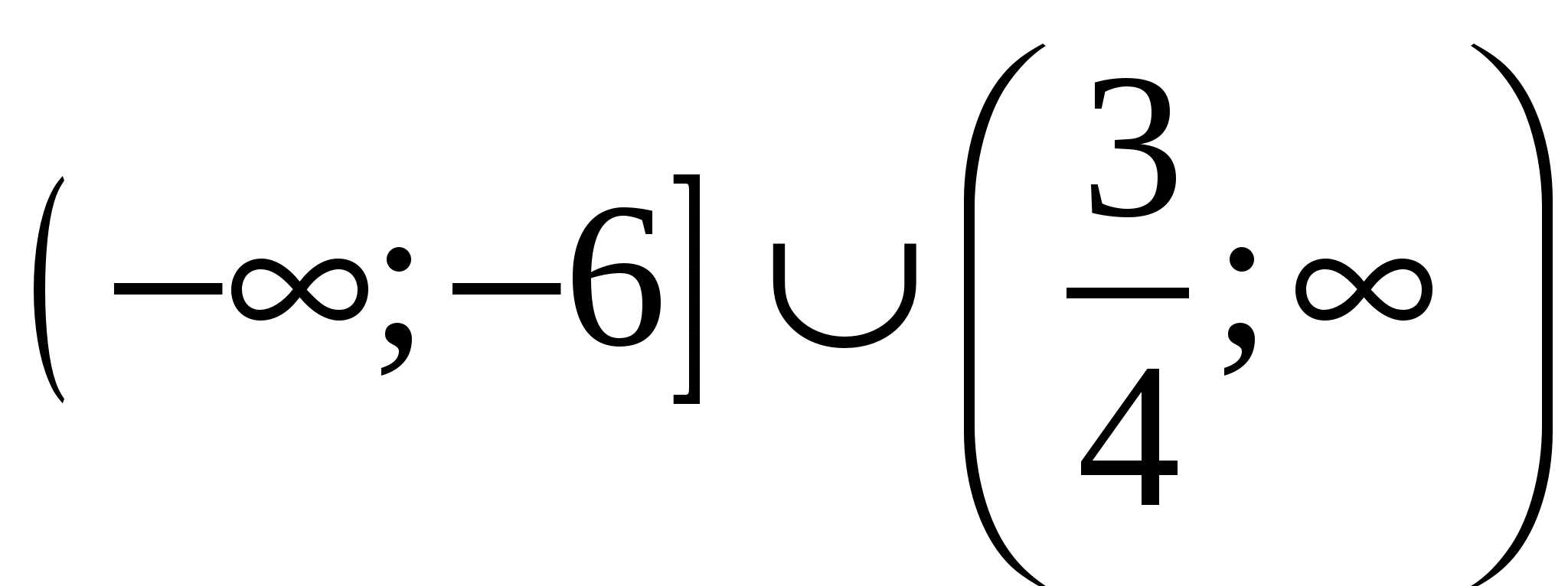
|
Найдите все значения параметра а, при которых система 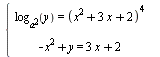 имеет ровно два решения. имеет ровно два решения.
|
Сравнение расположения графиков степенной и логарифмической функции. Потребуется применить математический анализ. Например, чтобы найти касание. Не забудьте случай убывающего логарифма!
|
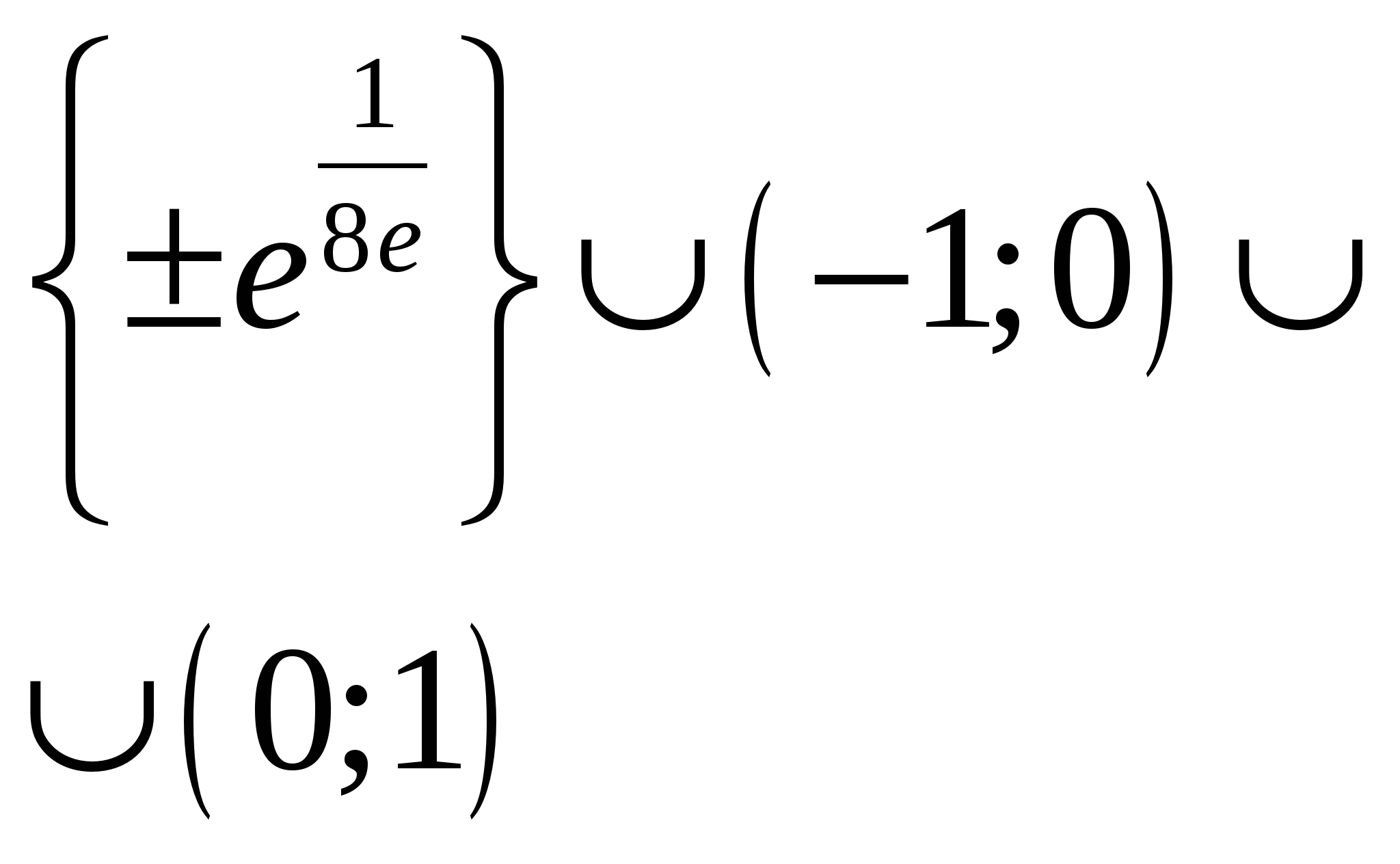
|
Найдите все значения параметра p, при каждом из которых уравнение 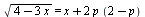 имеет ровно р корней. имеет ровно р корней.
|
Уравнение – хорошего типа: с различной монотонностью частей; следовательно, решений либо нет, либо одно. Рассмотрим две задачи уже без параметров, и найдем, нужное ли количество решений в каждом случае!
|
1
|
Найдите все значения параметра а, при которых система 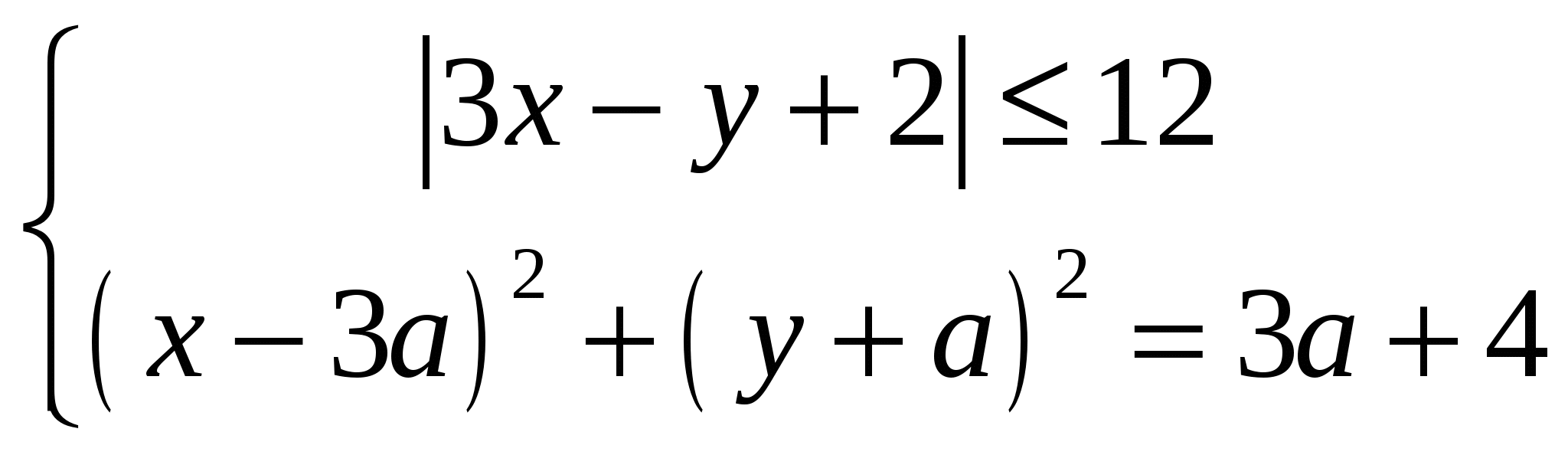 имеет единственное решение. имеет единственное решение.
|
Пересечение полосы и окружности, центр которой «бегает» по фиксированной прямой ( к счастью, прямая перпендикулярна границам полосы), а радиус зависит от параметра. Возможны два случая: либо окружность «стянулась» в точку, либо имеет место касание полосы внешним образом. Дальше дело техники….
|
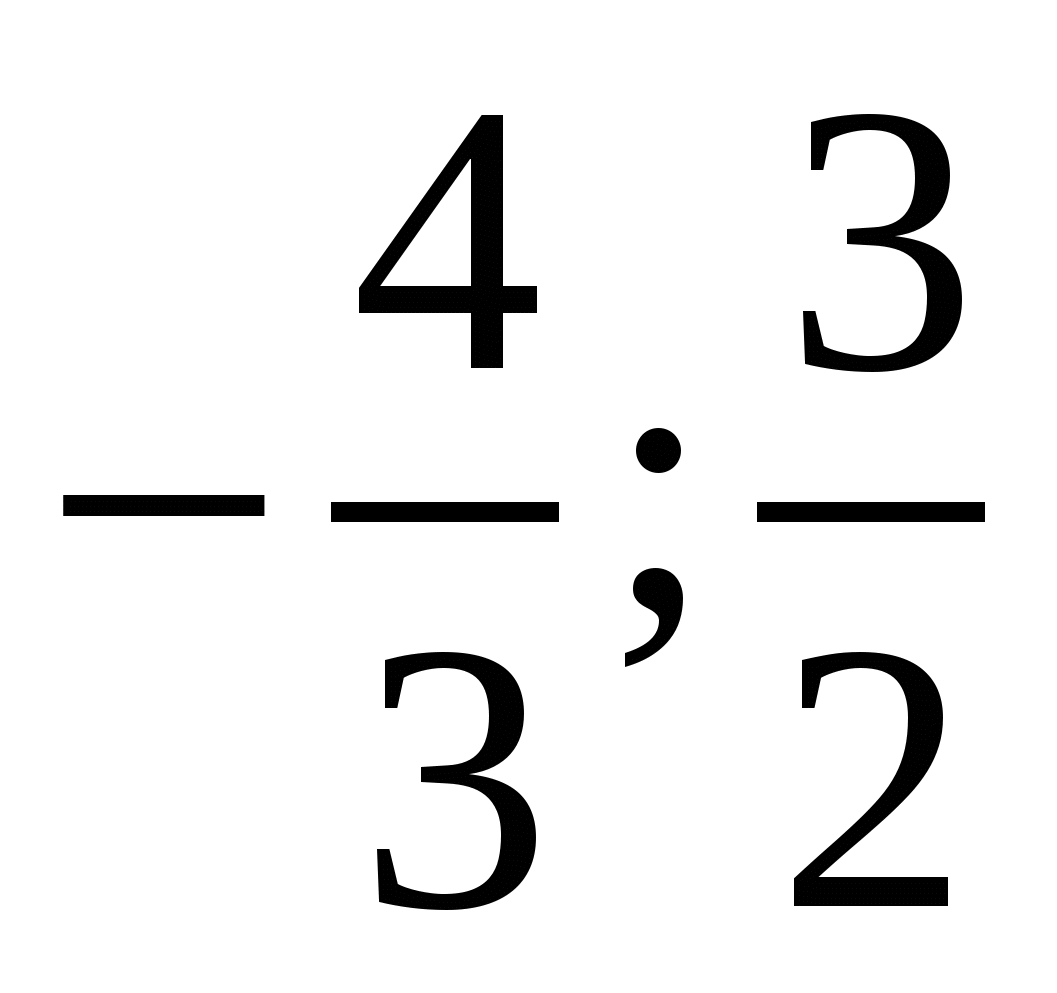
|
Пусть А - множество тех значений параметра а, для которых выполнено условие 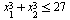 , где , где 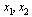 - действительные, различные корни уравнения - действительные, различные корни уравнения 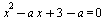 . Найдите множество значений, которое при этих условиях принимает величина . Найдите множество значений, которое при этих условиях принимает величина 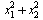 . .
|
Теорема Виета. Только надо учесть, что она работает только при наличии корней! График может помочь при решении, но он не является необходимостью.
|
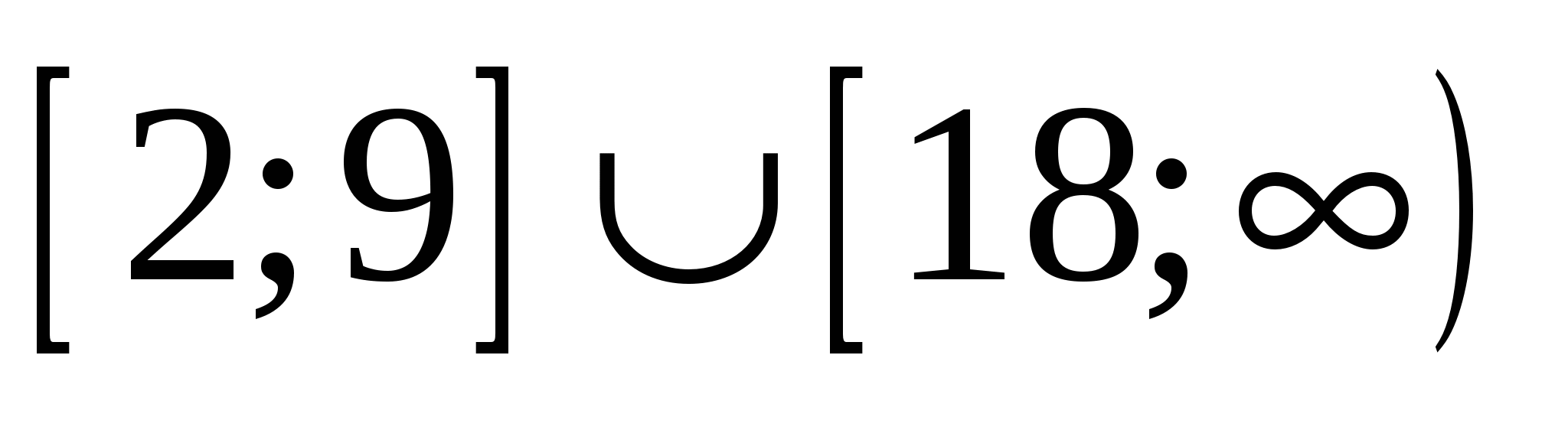
|
При каких значениях параметра  множество решений неравенства множество решений неравенства 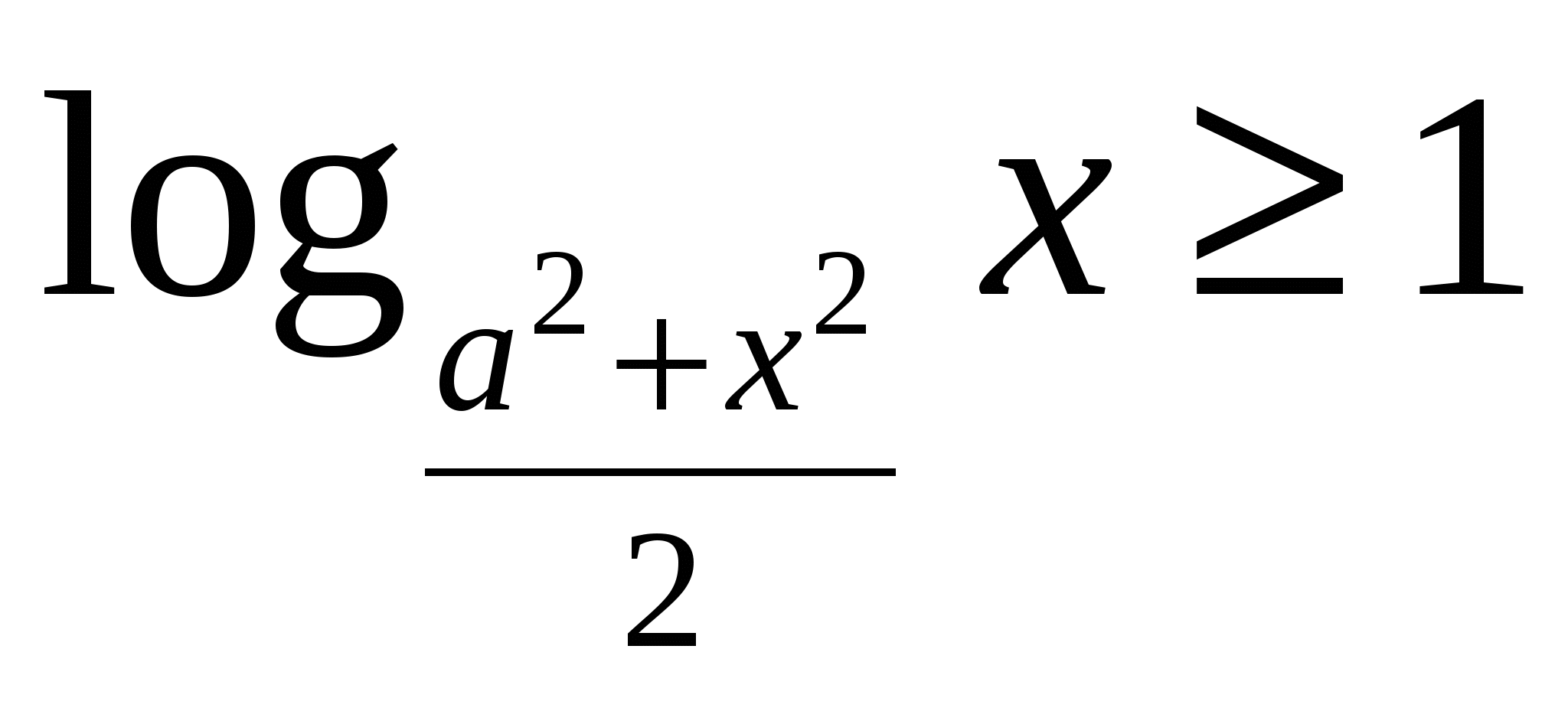 содержит не менее двух решений уравнения содержит не менее двух решений уравнения 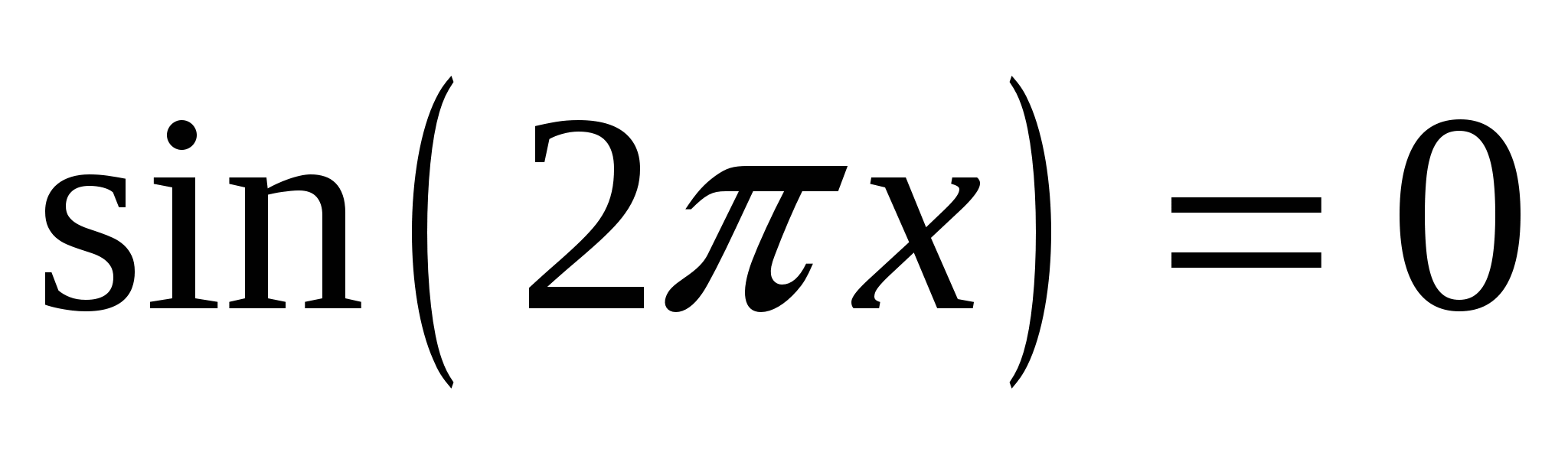 ? ?
|
Переходим к равносильной системе, строим график в осях переменная-параметр. Чем точнее он построен, тем легче увидеть отрезки вертикальных прямых по полуцелым точкам, получаемых из второго уравнения.
|
|
Найдите все значения параметра  , при каждом из которых множеством решений неравенства , при каждом из которых множеством решений неравенства 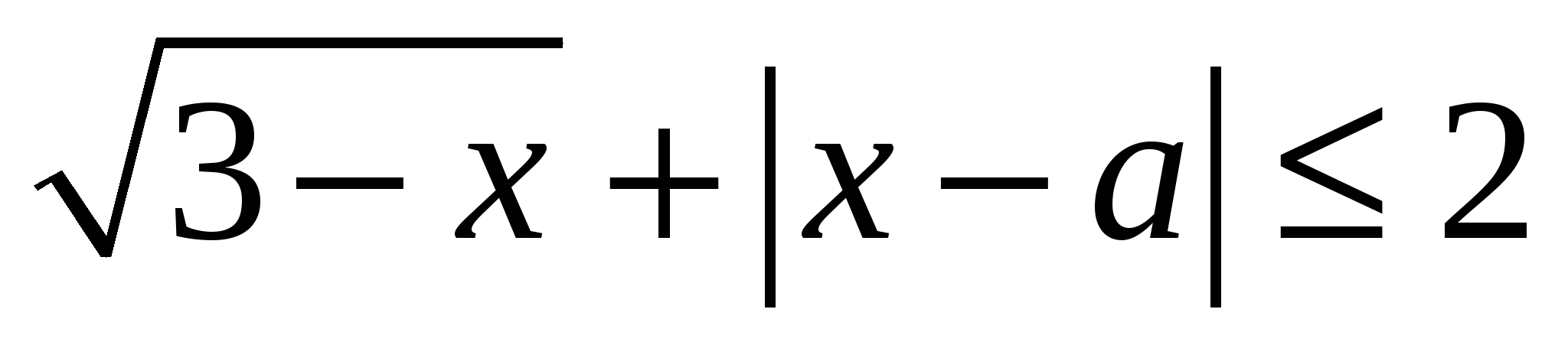 является отрезок. является отрезок.
|
Задачу удобно решать как в осях 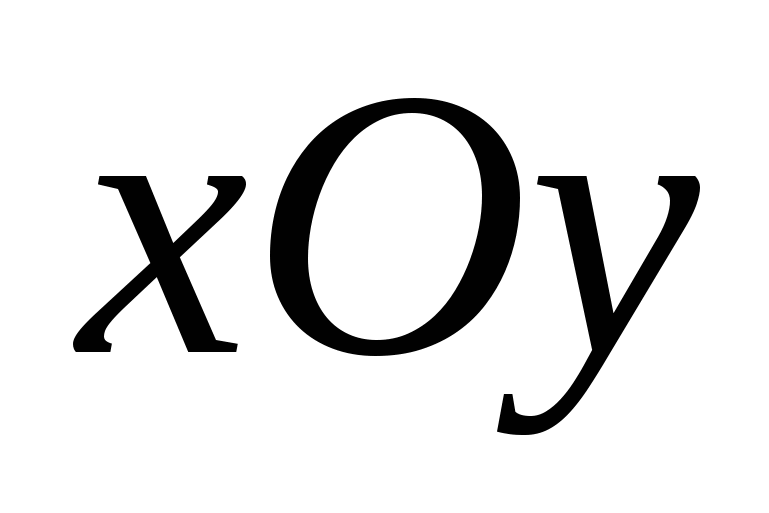 , двигая вдоль оси абсцисс «галочку», с нахождением касания и учетом области определения, так и построением в осях переменная-параметр ( с предварительной заменой корня на новую переменную). Конечно, и в том, и в другом варианте надо учитывать ограничения. , двигая вдоль оси абсцисс «галочку», с нахождением касания и учетом области определения, так и построением в осях переменная-параметр ( с предварительной заменой корня на новую переменную). Конечно, и в том, и в другом варианте надо учитывать ограничения.
|
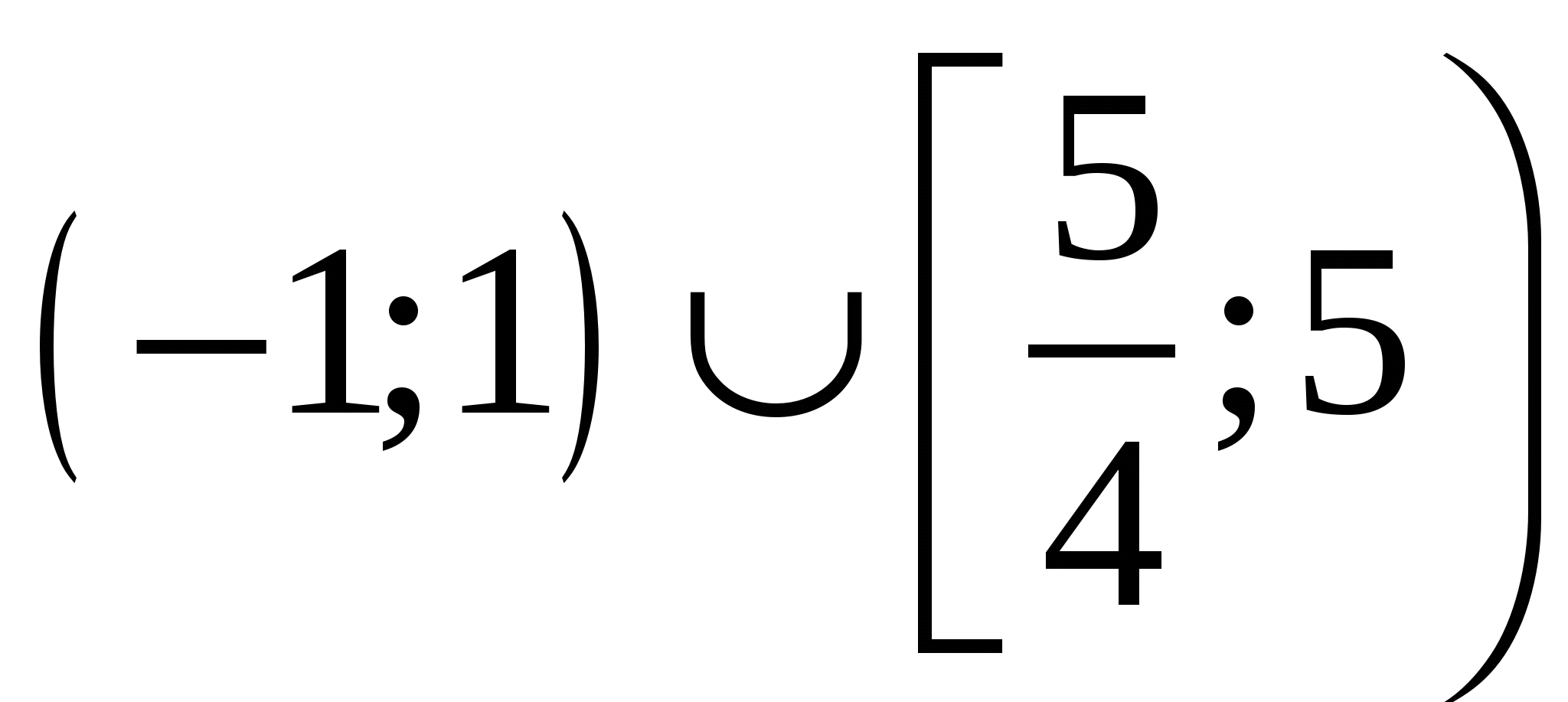
|
Блок 3. (домашнее задание)
|
Найдите все значения  , при каждом из которых уравнение , при каждом из которых уравнение 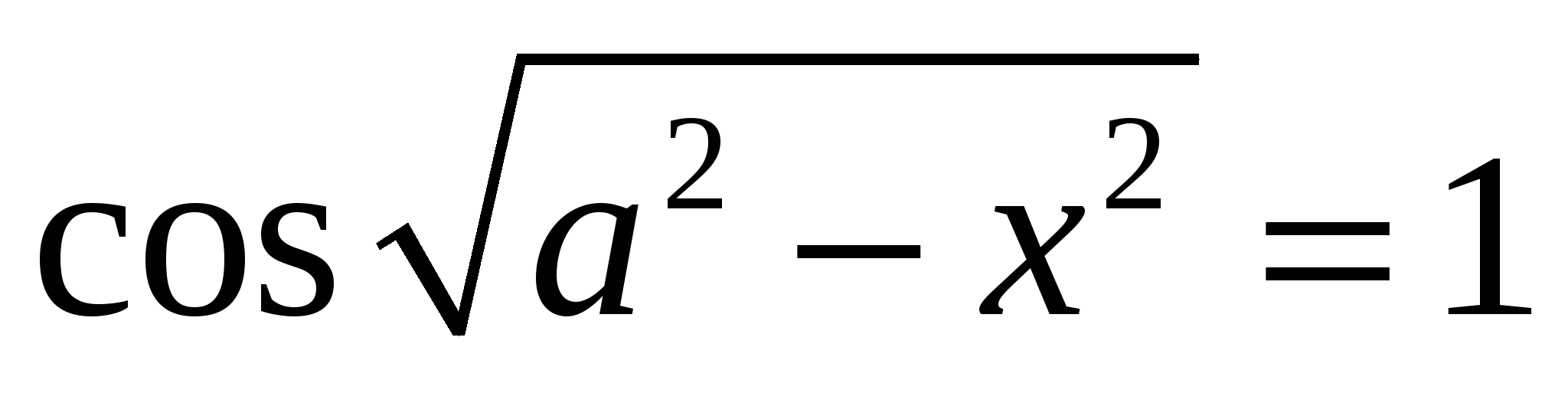 имеет ровно 6 решений. имеет ровно 6 решений.
|
|
Найдите все значения  , при каждом из которых уравнение , при каждом из которых уравнение 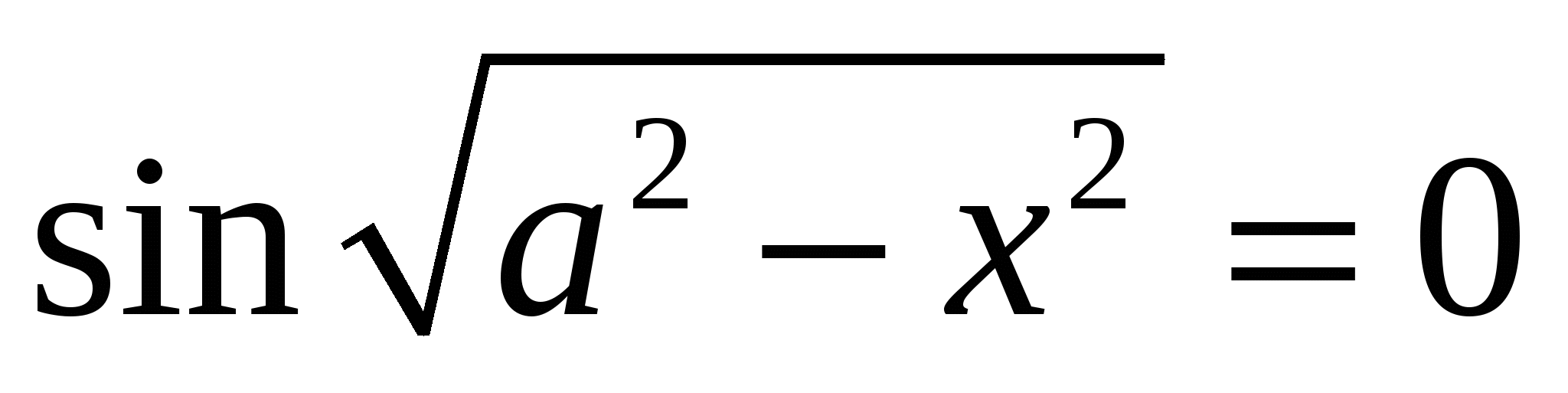 имеет ровно 10 решений. имеет ровно 10 решений.
|
|
Найдите все значения а, при каждом из которых система 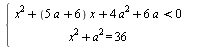 имеет решения. имеет решения.
|
|
Найдите все значения а, при каждом из которых система 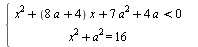 имеет решения. имеет решения.
|
|
Найдите все значения параметра а, при которых функция 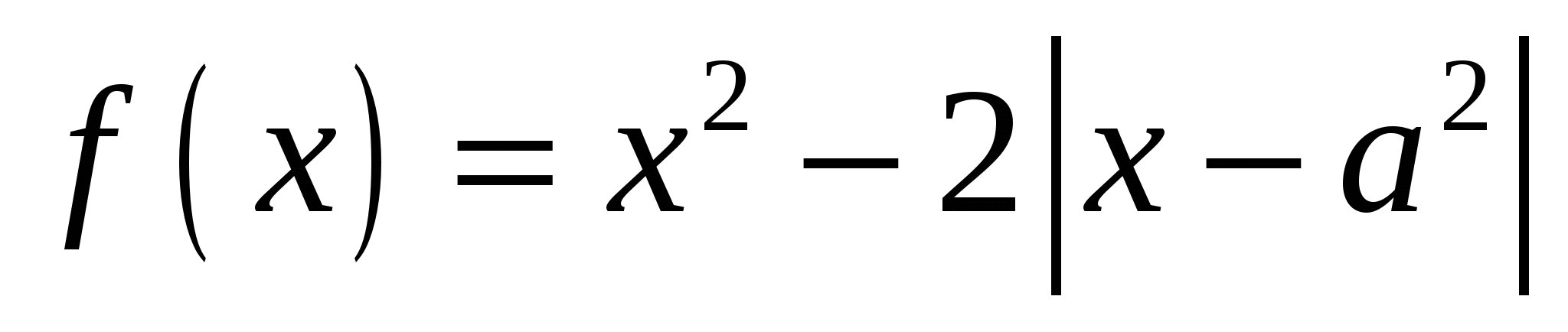 имеет хотя бы одну точку максимума. имеет хотя бы одну точку максимума.
|
|
Найдите все значения а, при которых система 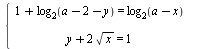 имеет решения. имеет решения.
|
|
Найдите все положительные значения а, при каждом из которых система 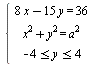 имеет единственное решение. имеет единственное решение.
|
|
Найдите все значения параметра a , при которых система уравнений 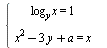 имеет два решения. имеет два решения.
|
|
Найдите все значения a, при каждом из которых функция 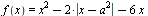 имеет более двух точек экстремума. имеет более двух точек экстремума.
|
|
Найдите все значения a, при каждом из которых наименьшее значение функции 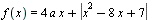 меньше 1. меньше 1.
|
|
Найдите все значения a, при каждом из которых наименьшее значение функции 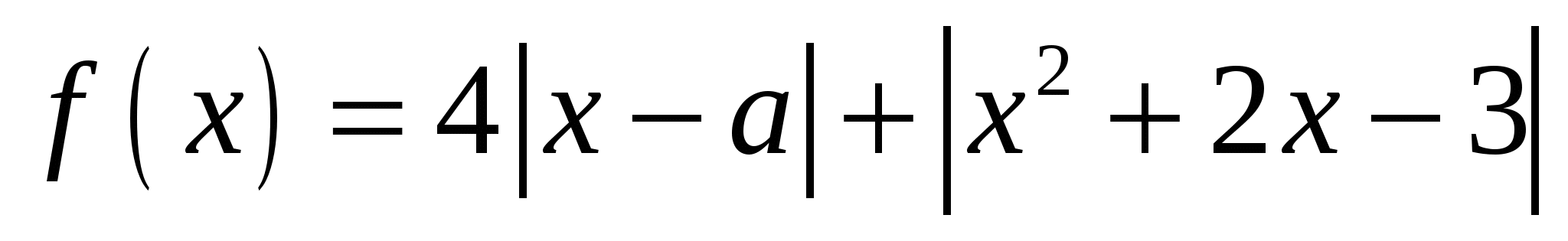 меньше 4. меньше 4.
|
|
Найдите все значения а, при каждом из которых ровно одно решение неравенства 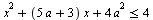 удовлетворяет неравенству удовлетворяет неравенству 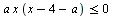 . .
|
|
Найдите наименьшее значение параметра a, при котором функция 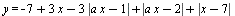 является неубывающей на всей числовой прямой. является неубывающей на всей числовой прямой.
|
|
Найдите все значения параметра а, при каждом из которых система 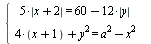 имеет ровно 8 решения. имеет ровно 8 решения.
|
|
Найдите все значения параметра а, при каждом из которых система 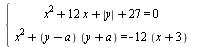 имеет ровно 4 решения. имеет ровно 4 решения.
|
|
Найдите все значения параметра а, при каждом из которых система 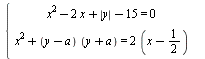 имеет ровно 6 решений. имеет ровно 6 решений.
|
|
Найдите все значения а, при каждом из которых любая прямая, перпендикулярная оси ординат, имеет нечетное число общих точек с графиком функции 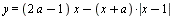 . .
|
|
Найдите все значения параметра а, при которых система 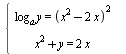 имеет ровно два решения. имеет ровно два решения.
|
|
Найдите все значения параметра а, при которых система 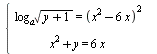 имеет ровно два решения. имеет ровно два решения.
|
|
Найдите все значения параметра а, при которых система неравенств 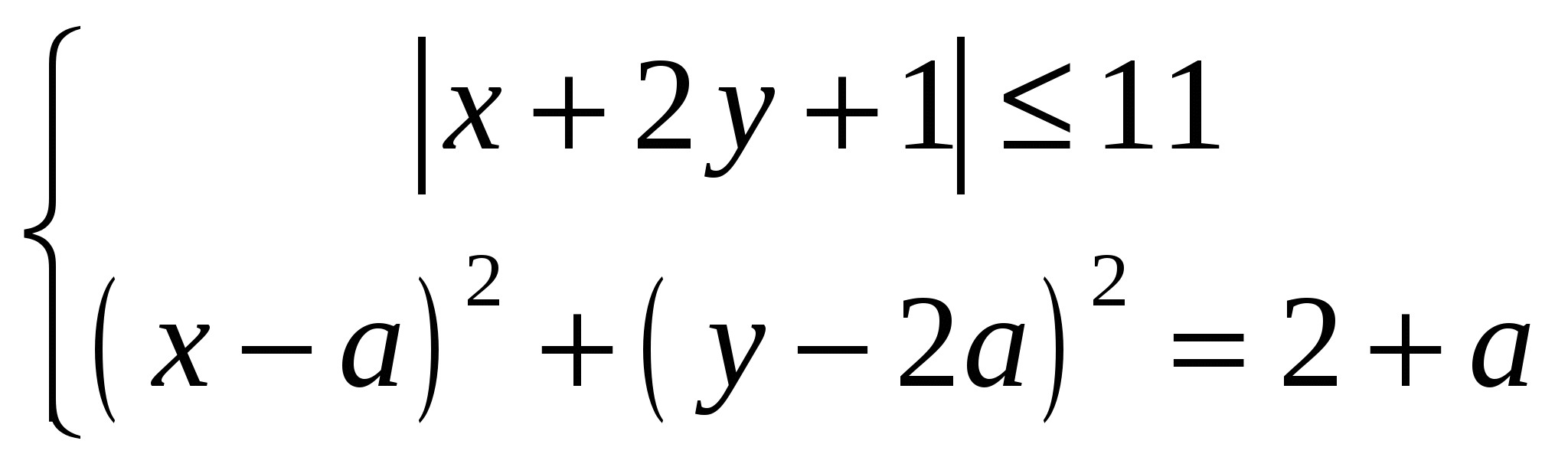 имеет единственное решение. имеет единственное решение.
|
|
Найдите все значения параметра а, при каждом из которых система 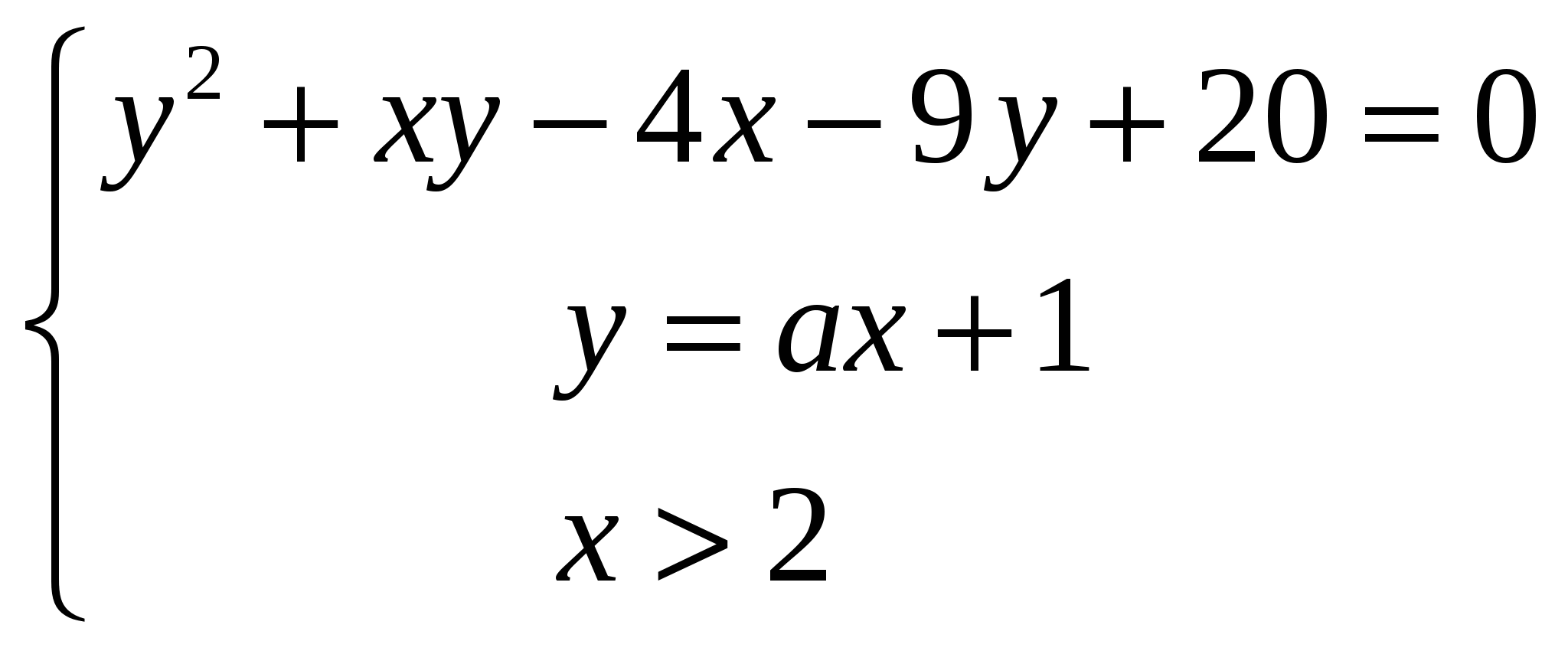 имеет единственное решение. имеет единственное решение.
|
|
Найдите все значения параметра а, при которых система 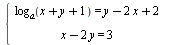 имеет единственное решение. имеет единственное решение.
|
|
При каких значениях параметра  множество решений неравенства множество решений неравенства 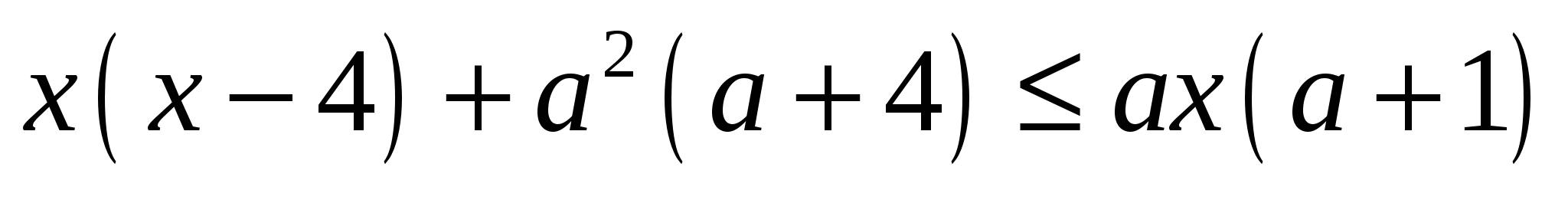 содержит не более четырех целых значений содержит не более четырех целых значений 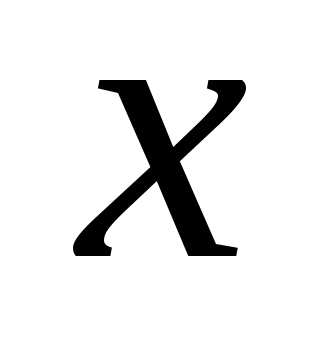 ? ?
|
|
Найдите все значения параметра  , при каждом из которых множеством решений неравенства , при каждом из которых множеством решений неравенства 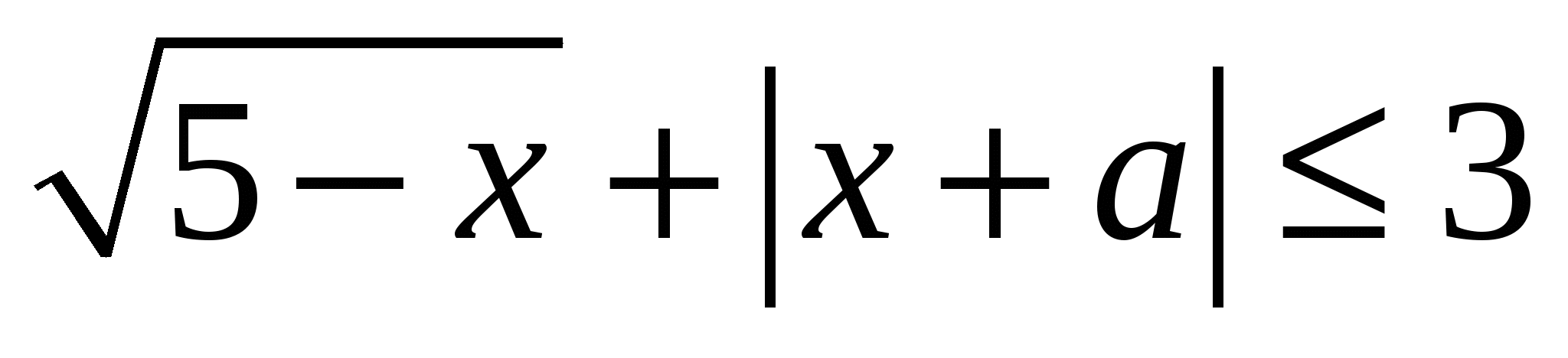 является отрезок. является отрезок.
|
|
Найдите все значения параметра а, при которых система 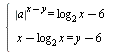 имеет ровно два решения. имеет ровно два решения.
|
|
 Скачать 160.56 Kb.
Скачать 160.56 Kb.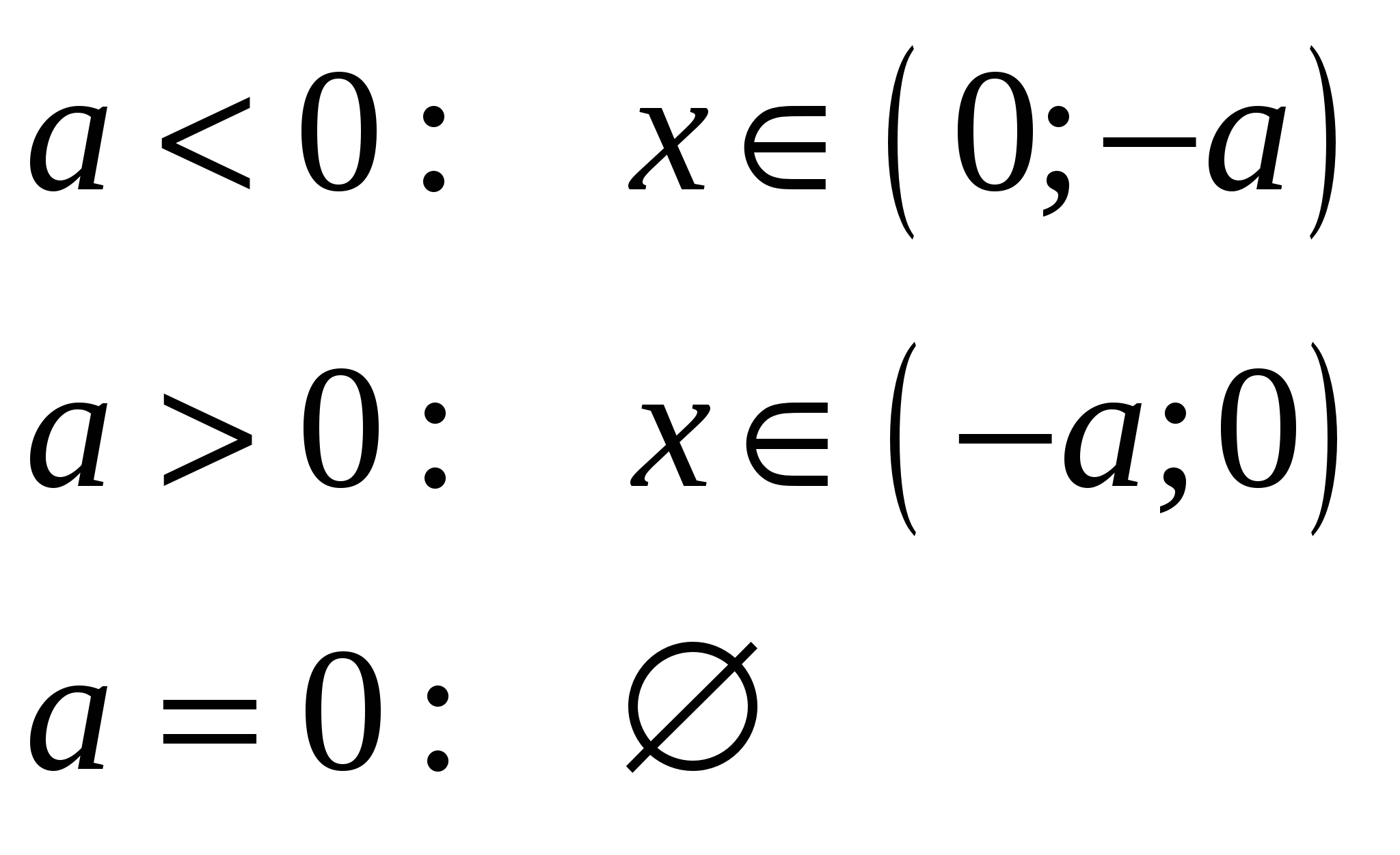
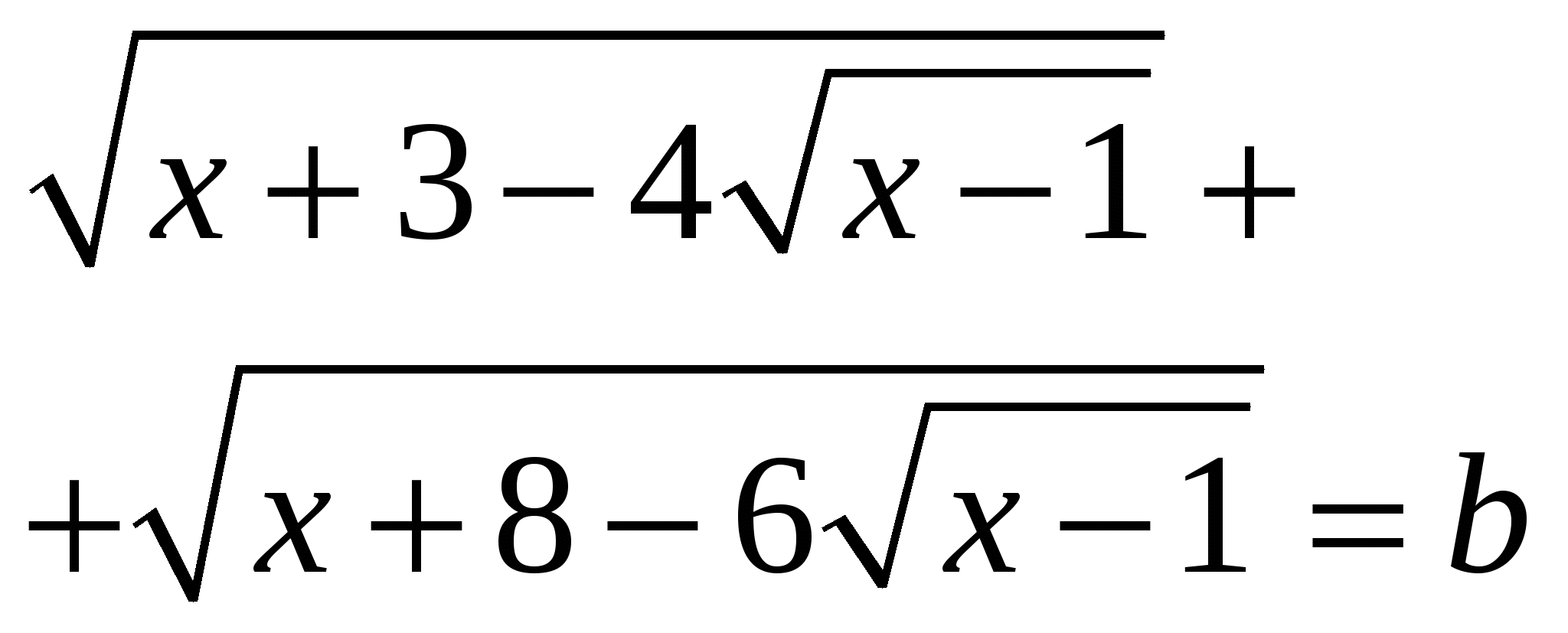 существуют и принадлежат отрезку |2;17].
существуют и принадлежат отрезку |2;17]. 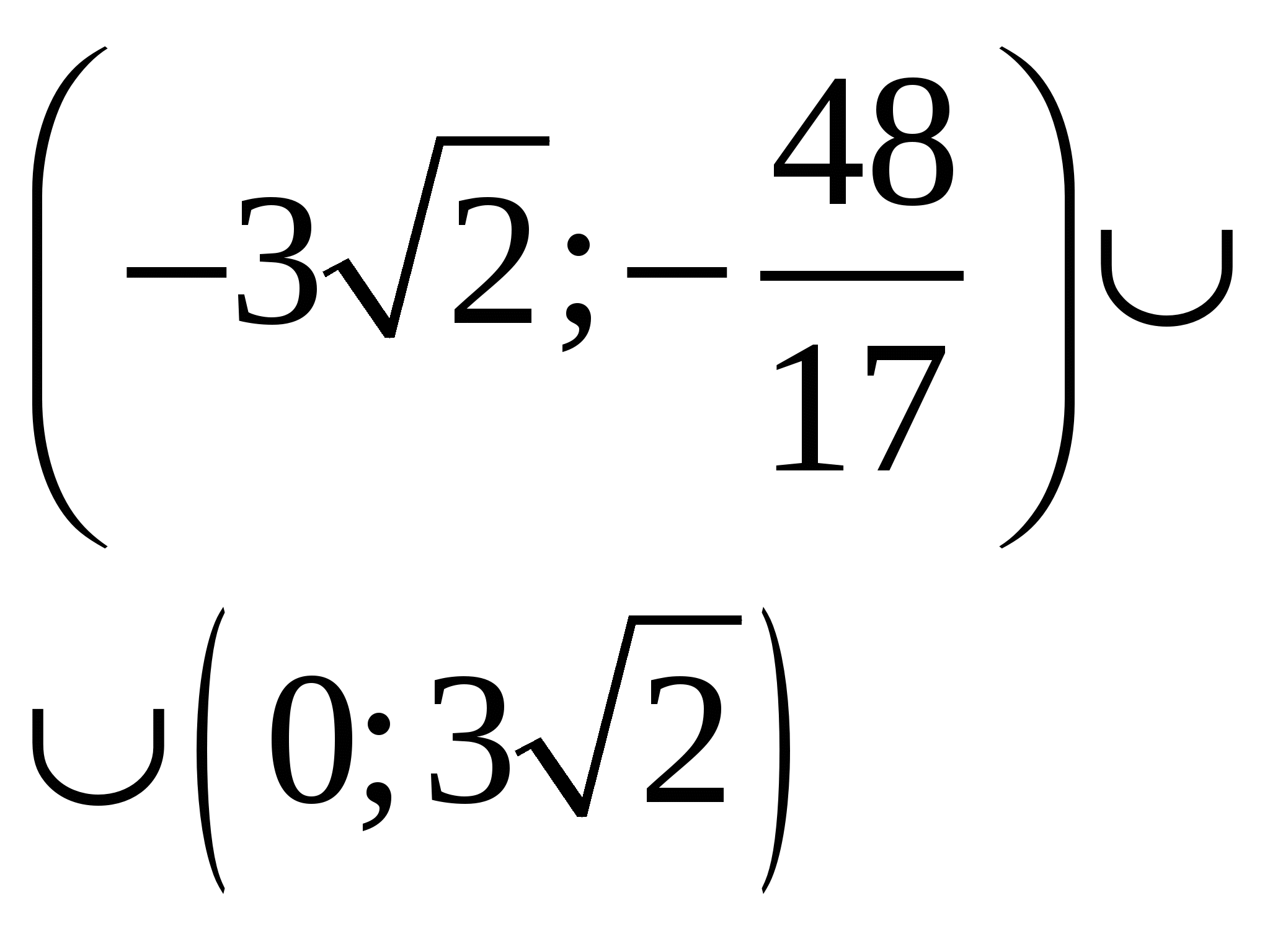
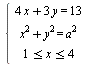 имеет единственное решение.
имеет единственное решение. 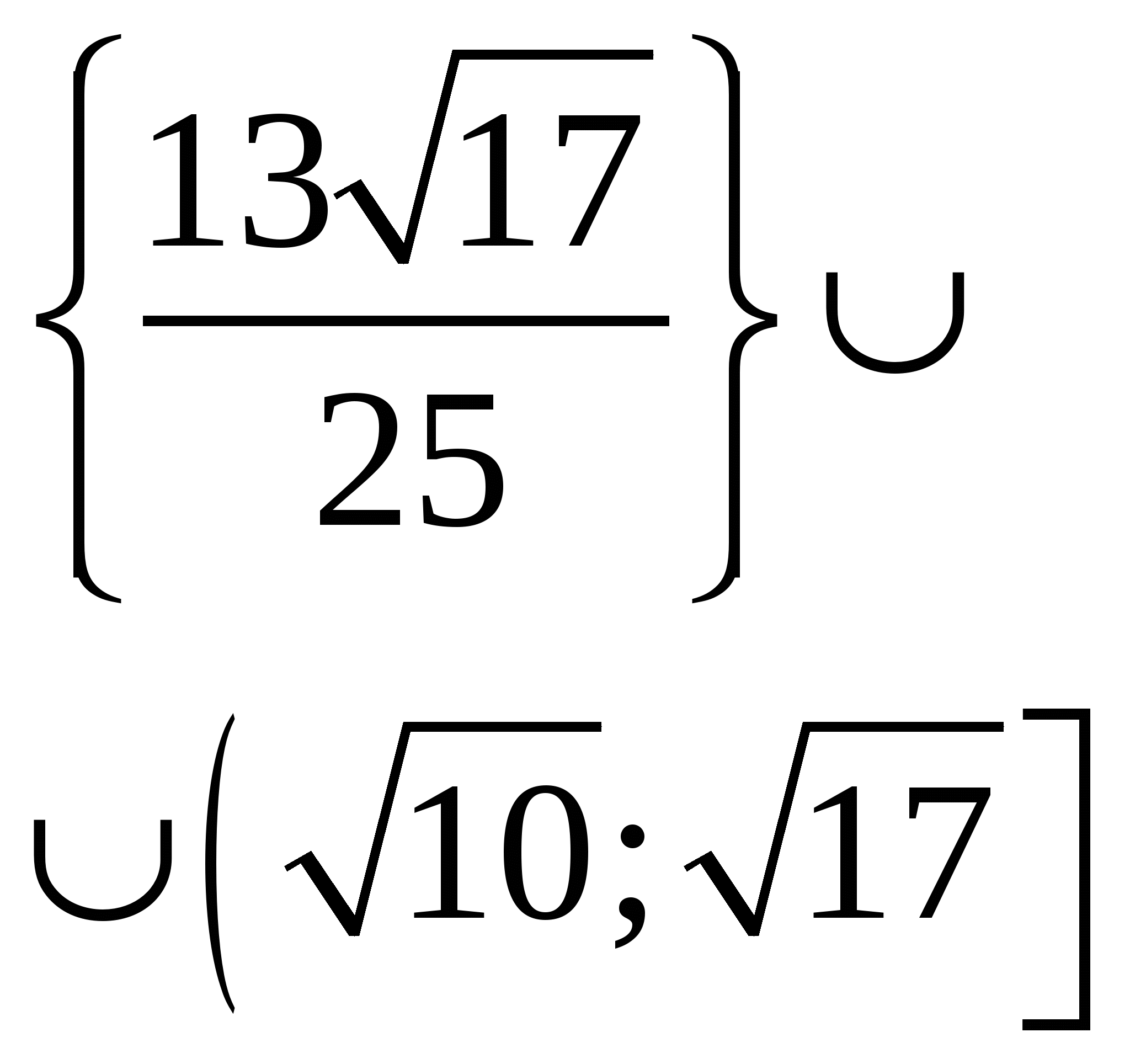
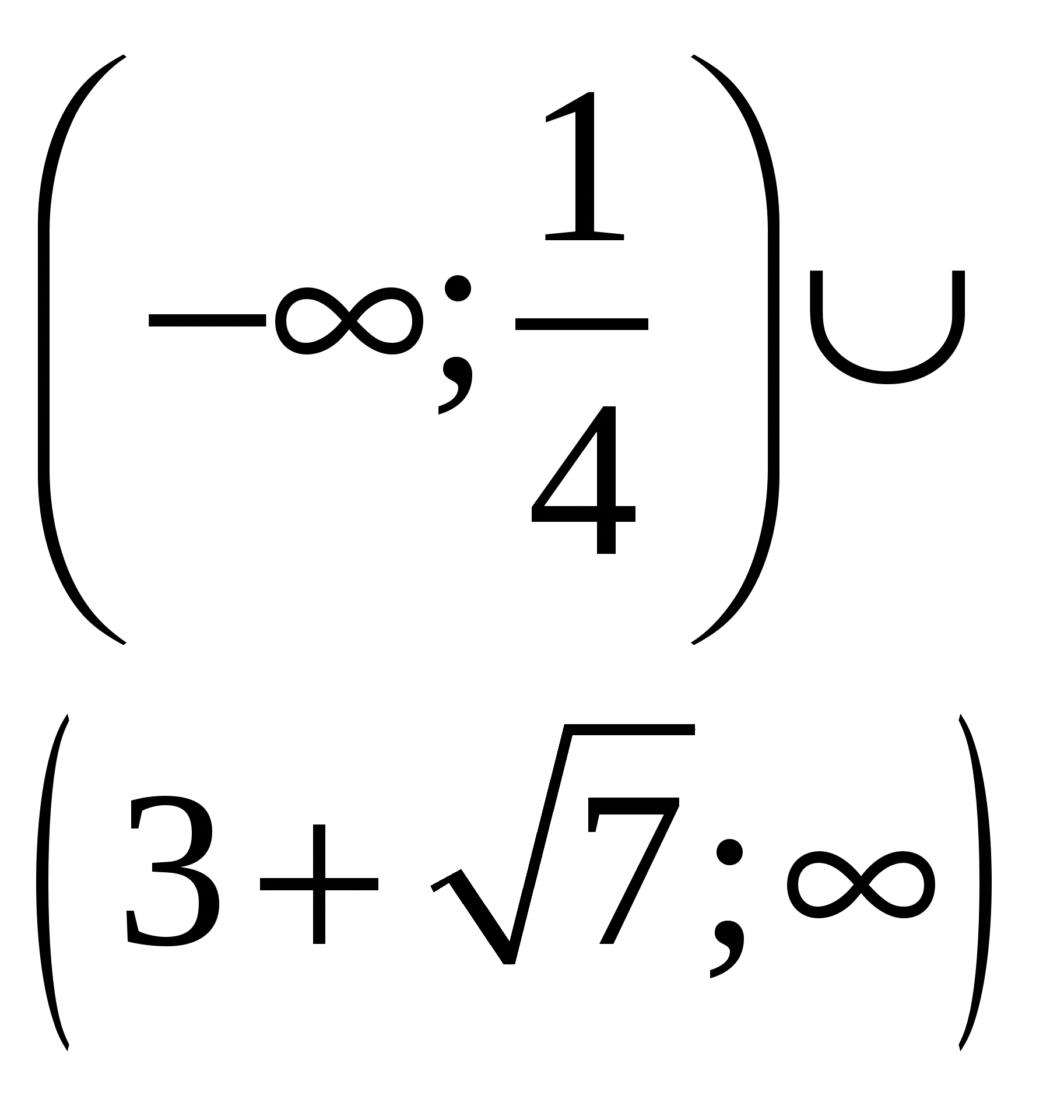
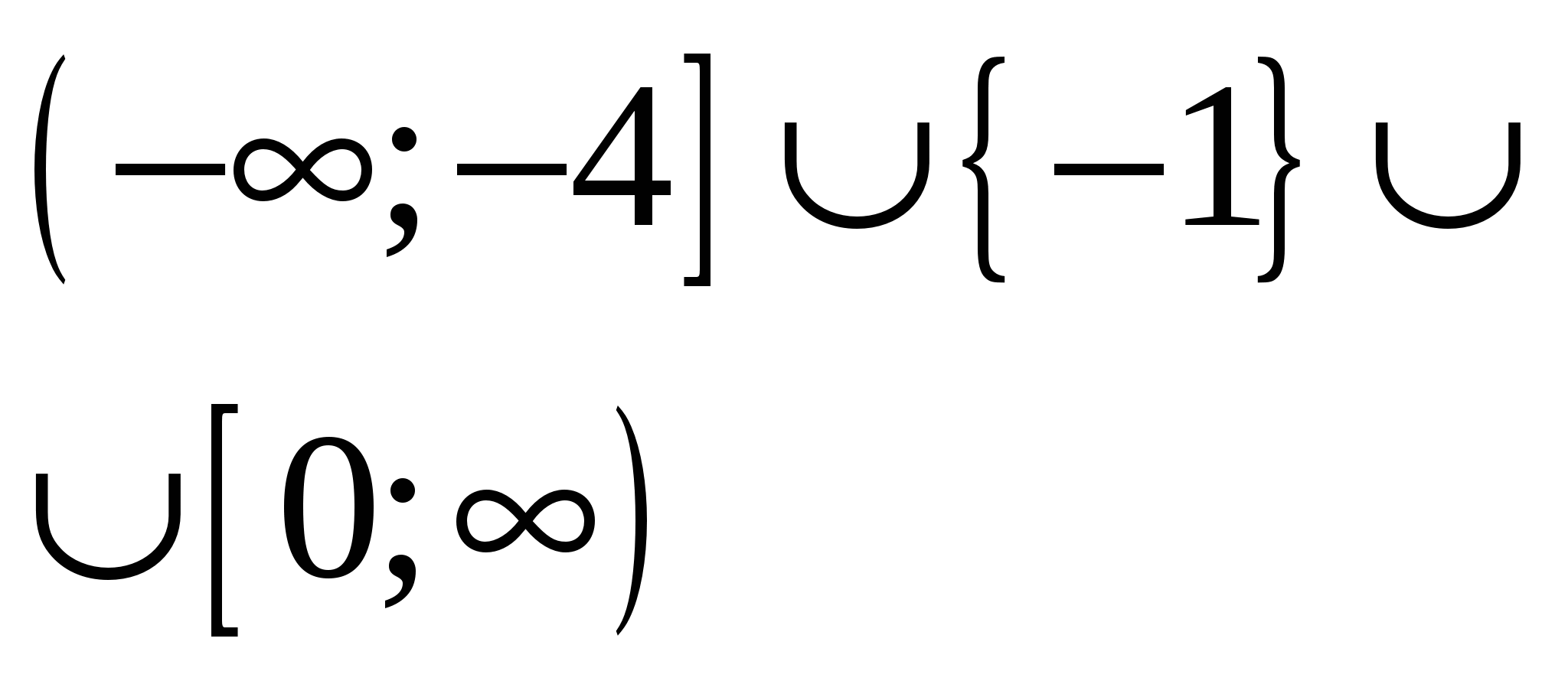
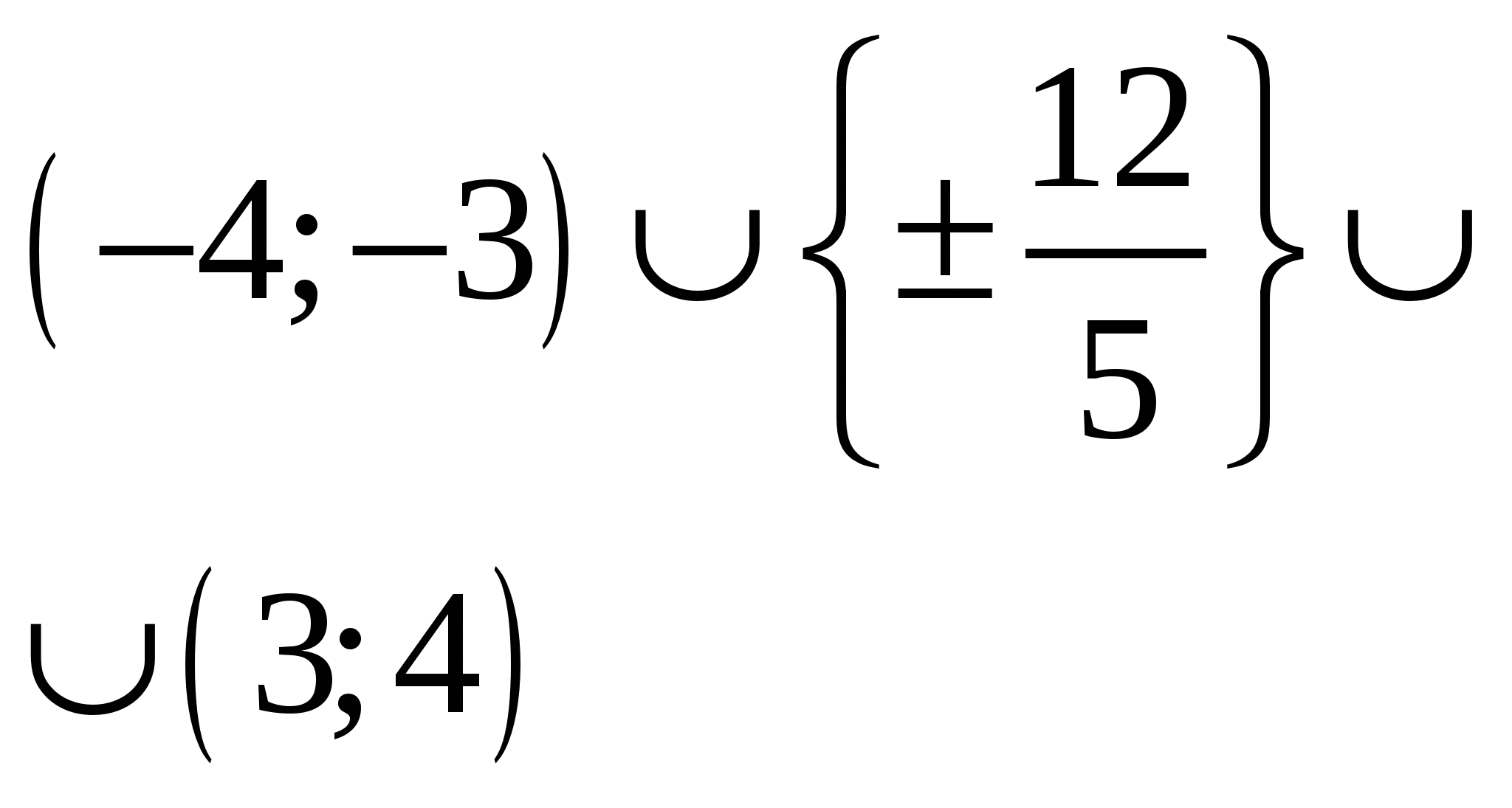
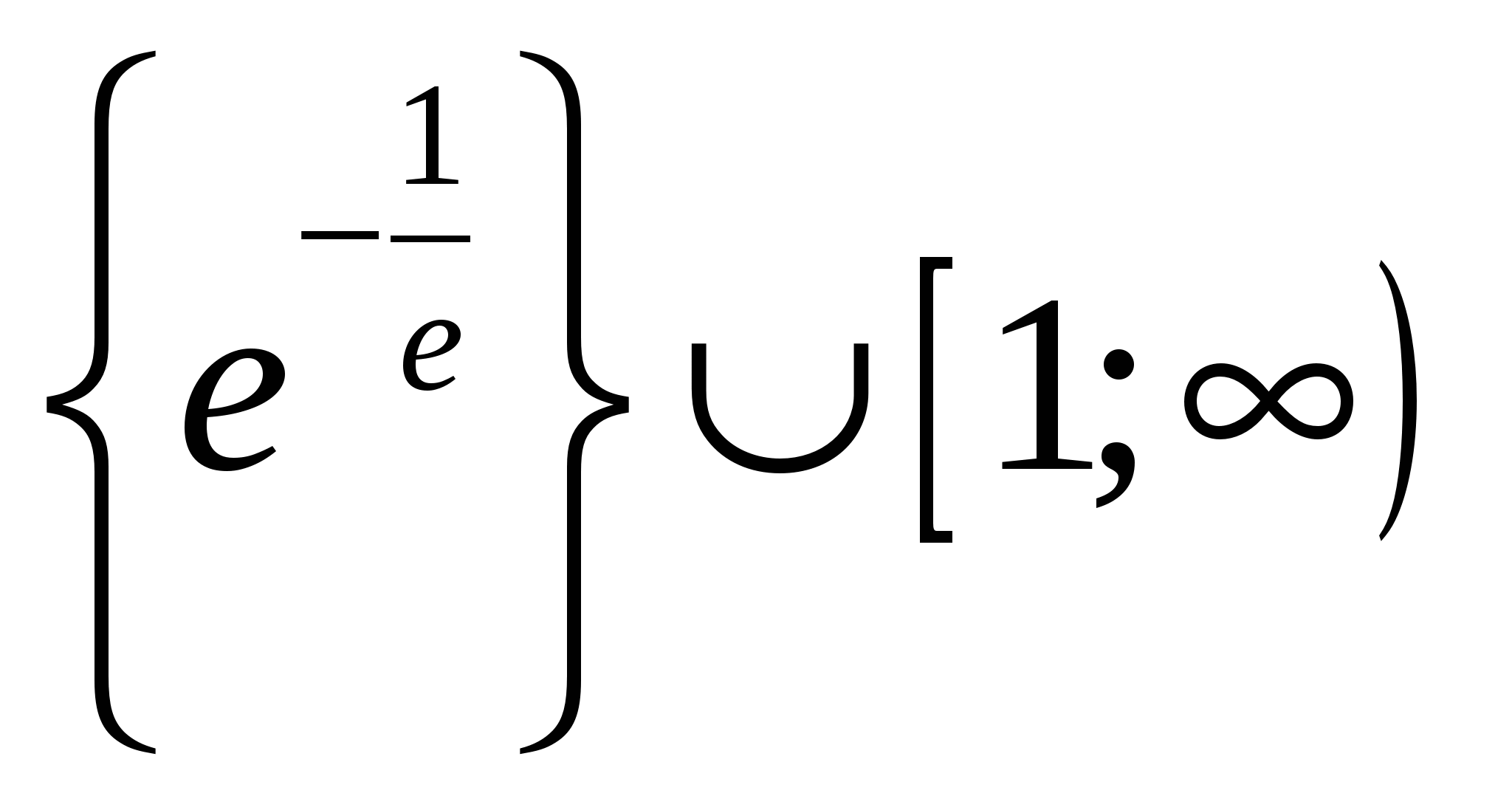
 имеет единственное решение. Найдите это значение параметра a и решите систему при найденном значении параметра.
имеет единственное решение. Найдите это значение параметра a и решите систему при найденном значении параметра. 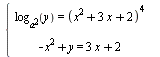 имеет ровно два решения.
имеет ровно два решения. 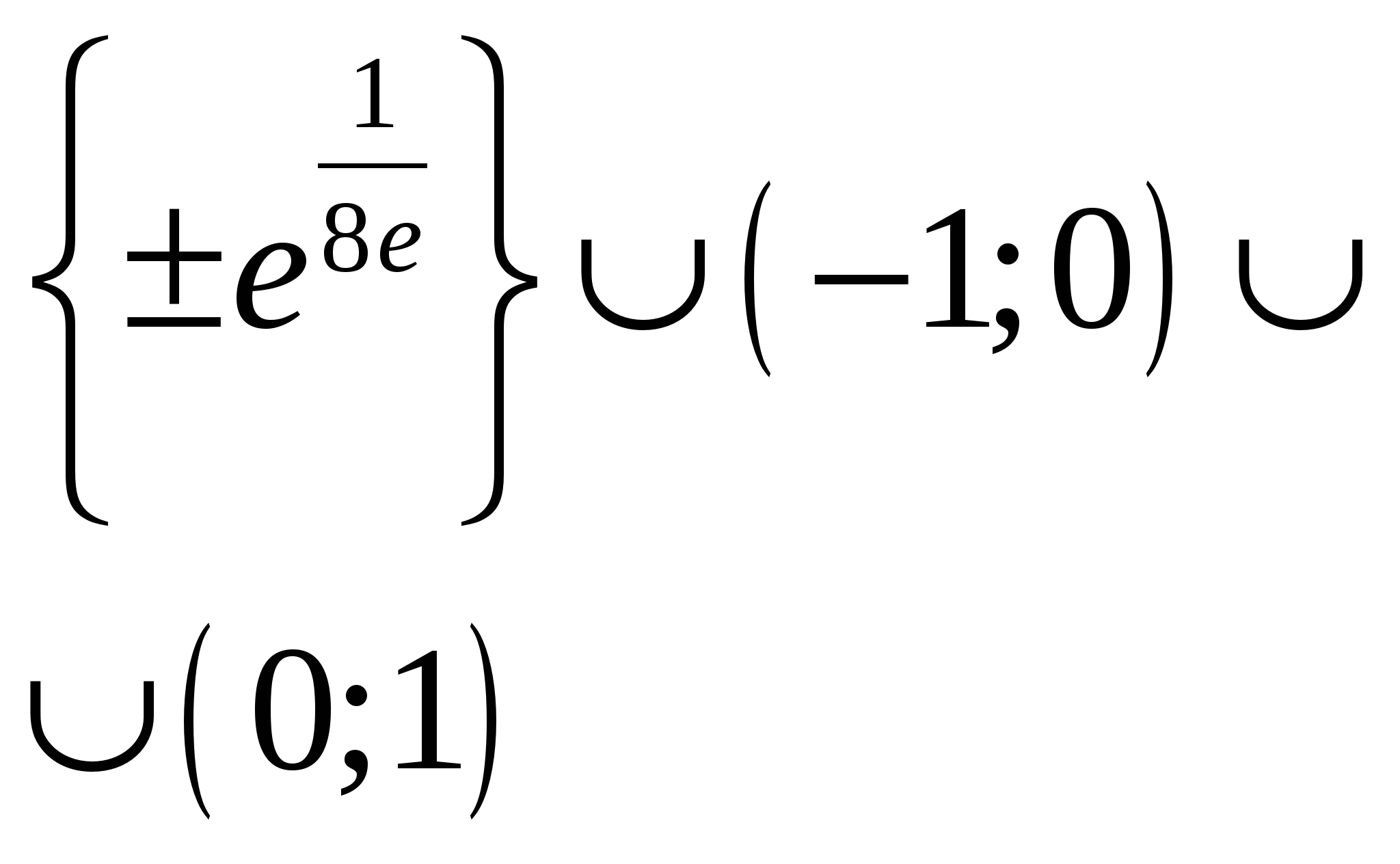
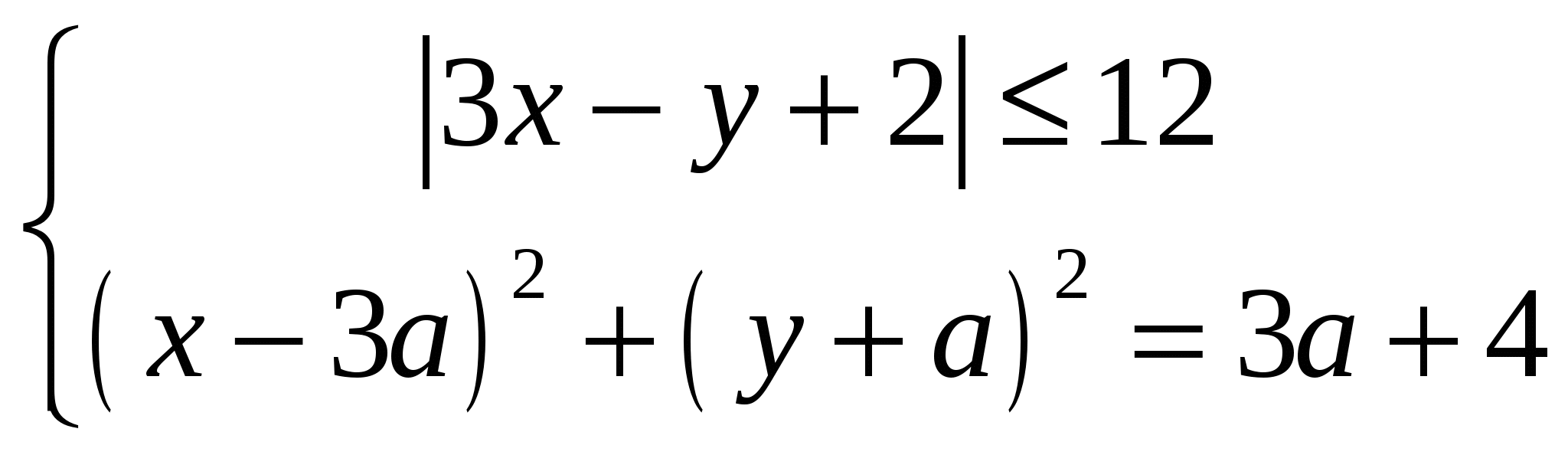 имеет единственное решение.
имеет единственное решение.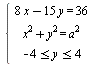 имеет единственное решение.
имеет единственное решение. 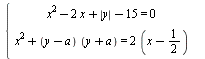 имеет ровно 6 решений.
имеет ровно 6 решений. 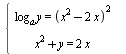 имеет ровно два решения.
имеет ровно два решения. 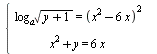 имеет ровно два решения.
имеет ровно два решения.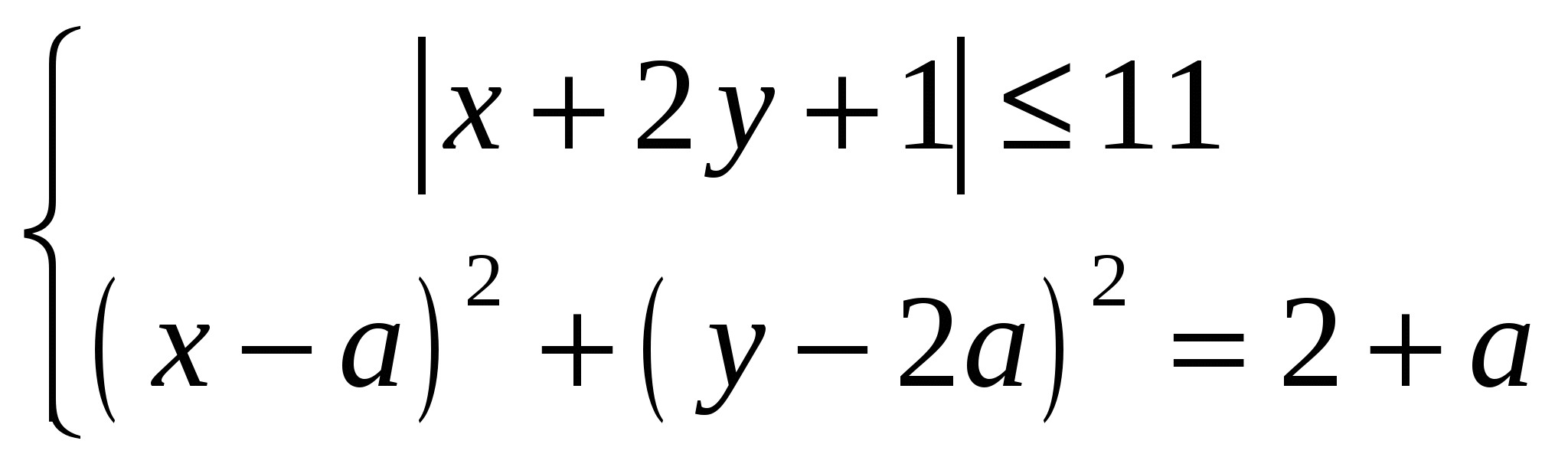 имеет единственное решение.
имеет единственное решение.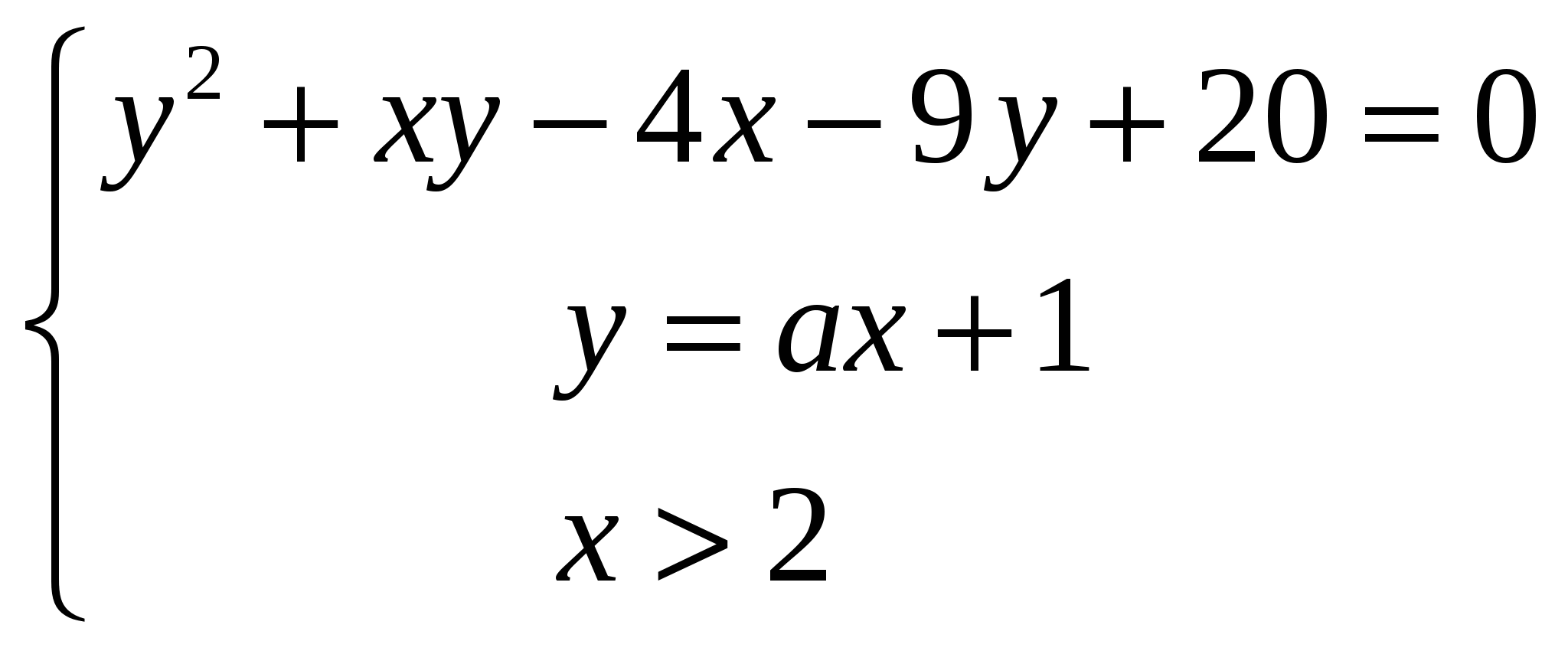 имеет единственное решение.
имеет единственное решение.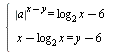 имеет ровно два решения.
имеет ровно два решения.