Учебник для студентов образовательных учреждений спо/С. Г. Григорьев, С. В. Иволгина; под редакцией В. А. Гусева 10-е изд., стер. М.: Издательский центр «Академия». 2014. 416 с
 Скачать 64.89 Kb. Скачать 64.89 Kb. |
Методические указания по проведениюпрактической работы № 5Решение прикладных задач (Приложения определенного интеграла)Цель работы: Используя теоретический материал и образцы решения задач, решить примеры по теме «Решение прикладных задач (Приложения определенного интеграла)» Перечень справочной литературы :
Краткие теоретические сведения: Вычисление площади плоской фигуры Найдем площадь S криволинейной трапеции, ограниченной кривой 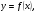 осью осью 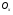 и двумя прямыми и двумя прямыми 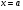 и и 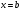 , где , где 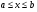 , , 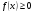 (рис. 1) (рис. 1) Так дифференциал переменной площади S есть площадь прямоугольника с основанием dx и высотой 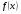 , т. е. , т. е. 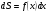 , то, интегрируя это равенство в пределах от a до b, получим , то, интегрируя это равенство в пределах от a до b, получим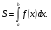 (1) Если криволинейная трапеция прилегает к оси 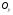 так, что так, что 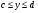 , , 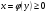 (рис. 2), то дифференциал переменной площади S равен (рис. 2), то дифференциал переменной площади S равен 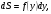 откуда откуда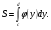 (2) В том случае, когда криволинейная трапеция, ограниченная кривой 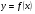 , осью , осью 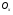 и прямыми x=a и x=b, лежит под осью и прямыми x=a и x=b, лежит под осью 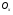 (рис. 3), площадь находится по формуле (рис. 3), площадь находится по формуле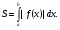 (3) Если фигура, ограниченная кривой 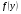 , осью , осью 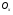 и прямыми x=a и x=b, расположена по обе стороны от оси и прямыми x=a и x=b, расположена по обе стороны от оси 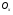 (рис. 4), то (рис. 4), то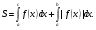 (4) Пусть, наконец, фигура S ограничена двумя пересекающимися кривыми 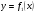 и и 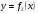 и прямыми x=a и x=b, где и прямыми x=a и x=b, где 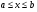 и и 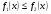 (рис. 5). Тогда ее площадь находится по формуле (рис. 5). Тогда ее площадь находится по формуле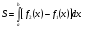 (5) Пример. Вычислить площадь фигуры, ограниченной указанными линиями 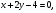 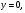 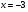 и и 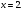 Решение. Выполним построение фигуры. Строим прямую 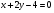 по двум точкам А(4;0) и В(0;2) (рис.6). Выразив у через х, получим по двум точкам А(4;0) и В(0;2) (рис.6). Выразив у через х, получим 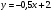 По формуле (1), где По формуле (1), где 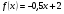 , , 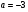 и и 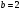 , находим , находим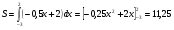 (кв. ед.) (кв. ед.)В качестве проверки вычислим площадь трапеции 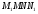 обычным путем. Находим: обычным путем. Находим: 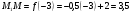 , , 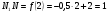 , , 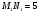 . Следовательно, . Следовательно, 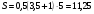 (кв. ед.). (кв. ед.).  Вычисление пути, пройденного точкой Путь, пройденный точкой при неравномерном движении по прямой с переменной скоростью 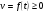 за промежуток времени от за промежуток времени от 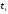 до до 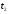 , вычисляется по формуле , вычисляется по формуле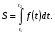 (6) Пример. Скорость движения точки изменяется по закону 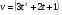 м/с. Найти путь, пройденный точкой за 10 с от начала движения. м/с. Найти путь, пройденный точкой за 10 с от начала движения.Решение. Согласно условию, 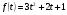 , , 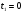 , , 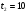 . По формуле (6) находим . По формуле (6) находим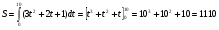 (м). (м).Вычисление работы силы Работа, произведенная переменной силой 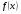 при перемещении по оси при перемещении по оси 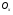 материальной точки от материальной точки от 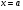 до до 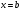 , находится по формуле , находится по формуле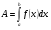 (7) (7)При решении задач на вычисление работы силы часто используется закон Гука: 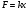 , (8) , (8)где F - сила, H; x - абсолютное удлинение пружины, м, вызванное силой F, а k - коэффициент пропорциональности, Н/м. Пример. Сжатие х винтовой пружины пропорционально приложенной силе F. Вычислить работу силы F при сжатии пружины на 0,04 м, если для сжатия ее на 0,01 м нужна сила 10 Н. Решение. Так как, 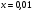 м при м при 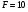 Н, то, подставляя эти значения в равенство (8), получим Н, то, подставляя эти значения в равенство (8), получим 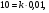 откуда откуда 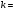 1000 Н/м. Подставив теперь в это же равенство значение k, находим 1000 Н/м. Подставив теперь в это же равенство значение k, находим 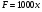 , т. е. , т. е. 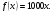 Искомую работу найдем по формуле (7), полагая Искомую работу найдем по формуле (7), полагая 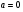 , , 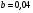 : :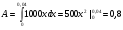 (Дж). (Дж).Вычисление работы, производимой при поднятии груза Пример. Цилиндрическая цистерна с радиусом основания 0,5 м и высотой 2 м заполнена водой. Вычислить работу, которую необходимо произвести, чтобы выкачать воду из цистерны. Решение. Выделим на глубине х горизонтальный слой высотой dx (рис. 7). Работа А, которую надо произвести, чтобы поднять слой воды весом Р на высоту х, равна 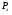 . .Изменение глубины х на малую величину dx вызовет изменение объема V на величину 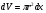 и изменение веса Р на величину и изменение веса Р на величину 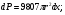 при этом совершаемая работа А изменится на величину при этом совершаемая работа А изменится на величину 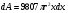 Проинтегрировав это равенство при изменении х от 0 до Н, получим 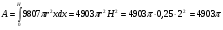 (Дж). (Дж).Вычисление силы давления жидкости Значение силы Р давления жидкости на горизонтальную площадку зависит от глубины погружения х этой площадки, т. е. от расстояния площадки до поверхности жидкости. Сила давления (Н) на горизонтальную площадку вычисляется по формуле 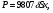 где 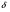 - плотность жидкости, - плотность жидкости, 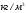 ; S площадь площадки, ; S площадь площадки, 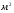 ; х - глубина погружения площадки, м. ; х - глубина погружения площадки, м.Если площадка, испытывающая давление жидкости, не горизонтальна, то давление на нее различно на разных глубинах, следовательно, сила давления на площадку есть функция глубины ее погружения Р(х). Пример. Вычислить силу давления воды на вертикальный прямоугольный шлюз с основанием 20 м и высотой 5 м (уровень воды совпадает с верхним обрезом шлюза). Решение. На глубине х выделим горизонтальную полоску шириной dx (рис 8). Сила давления Р на стенку шлюза есть функция от х. Изменение глубины х на малую величину dx вызовет изменение силы давления Р на малую величину 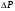 . . Продифференцировав переменную Р, получим приближенное значение (главную часть) 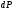 приращения приращения 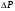 . .Находим приближенное значение силы давления воды на эту полоску: 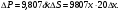 Но Но 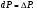 Интегрируя Интегрируя 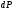 при изменении х от 0 до 5, получим при изменении х от 0 до 5, получим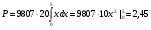 (МН). (МН).Длина дуги плоской кривой Пусть плоская кривая АВ (рис. 9) задана уравнением 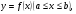 причем причем 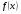 и и 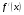 - непрерывные функции в промежутке - непрерывные функции в промежутке 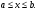 Тогда дифференциал Тогда дифференциал 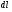 длины дуги АВ выражается формулой длины дуги АВ выражается формулой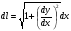 или или 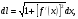 а длина дуги АВ вычисляется по формуле 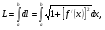 (9) (9)где 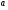 и и 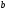 - значения независимой переменной х в точках А и В. - значения независимой переменной х в точках А и В.Если кривая задана уравнением 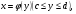 то длина дуги АВ вычисляется по формуле то длина дуги АВ вычисляется по формуле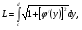 (10) где c и d – значения независимой переменной у в точках А и В. Пример. Найти длину окружности 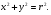 Решение. Дифференцируя уравнение окружности, имеем 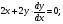 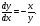 По формуле (9) вычислим длину дуги четверти окружности, взяв пределы интегрирования от 0 до r: 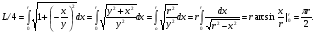 Длина окружности равна 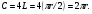 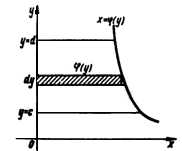 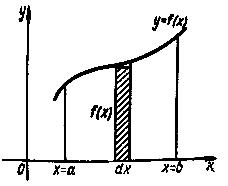 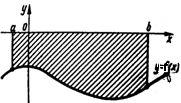 (рис. 1) (рис. 2) (рис. 3) 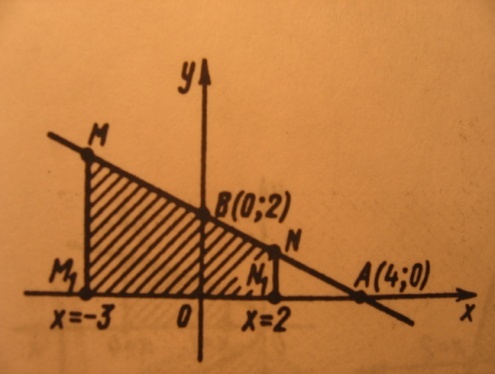 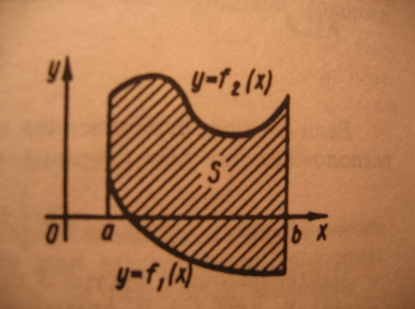 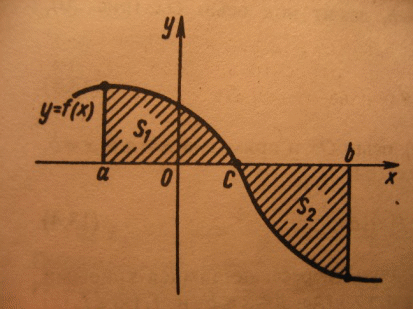 (рис. 4) (рис. 5) (рис. 6) 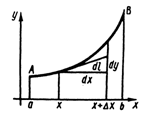 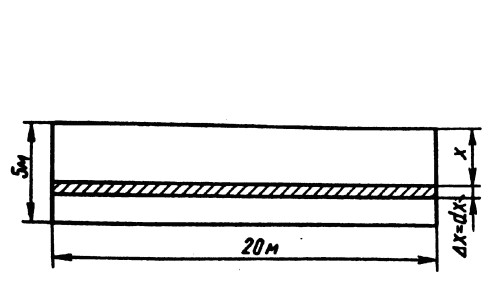 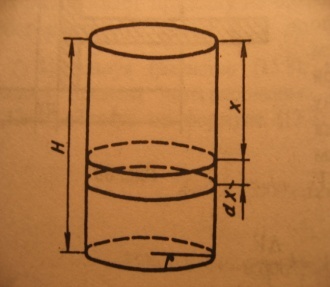 (рис. 7) (рис. 8) (рис. 9) Порядок проведения работы:
Оформление работы:
| ||||||||||||||||||||||