Решение егэ информатика
 Скачать 0.52 Mb. Скачать 0.52 Mb.
|
| По яс не ние. Если A[i] эле мент мас си ва мень ше A[0], то про грам ма ме ня ет их ме ста ми и уве ли чи ва ет зна че ние пе ре мен ной c на 1. Про грам ма вы пол нит ся два жды, пер вый раз по ме няв ме ста ми A[0] и A[2], так как 3<4, и вто рой раз по ме няв A[0] и A[5] (0<3). Таким об ра зом зна че ние пе ре мен ной с ста нет равно 2. Ответ: 2. 20. За да ние Ниже на пяти язы ках про грам ми ро ва ния за пи сан ал го ритм. По лу чив на вход число x, этот ал го ритм пе ча та ет число M. Из вест но, что x > 100. Ука жи те наи мень шее такое (т.е. боль шее 100) число x, при вводе ко то ро го ал го ритм пе ча та ет 26.
По яс не ние. В теле цикла числа M и L умень ша ют ся, пока не ста нут рав ны ми. Чтобы в итоге было на пе ча та но 26, оба числа в какой-то мо мент долж ны быть равны 26. Пой дем от конца к на ча лу: на преды ду щем шаге одно число было 26, а дру гое 26 + 26 = 52. Еще на шаг рань ше 52 + 26 = 78 и 52. До того 78 + 52 = 130 и 52. То есть наи мень шее воз мож ное число 130. А по сколь ку най ден ное число чет ное, то M будет при сво е но зна че ние 52, что и при ве дет к не об хо ди мо му ре зуль та ту. Ответ: 130. 21. За да ние На пи ши те в от ве те наи мень шее зна че ние вход ной пе ре мен ной k, при ко то ром про грам ма выдаёт тот же ответ, что и при вход ном зна че нии k = 10. Для Ва ше го удоб ства про грам ма при ве де на на пяти язы ках про грам ми ро ва ния.
По яс не ние. Дан ная про грам ма срав ни ва ет При k = 10, про грам ма вы ве дет число 3. За пи шем не ра вен ство: Ответ: 3. 22. За да ние Ис пол ни тель Май15 пре об ра зу ет число на экра не. У ис пол ни те ля есть две ко ман ды, ко то рым при сво е ны но ме ра: 1. При ба вить 1 2. Умно жить на 2 Пер вая ко ман да уве ли чи ва ет число на экра не на 1, вто рая умно жа ет его на 2. Про грам ма для ис пол ни те ля Май15 – это по сле до ва тель ность ко манд. Сколь ко су ще ству ет про грамм, для ко то рых при ис ход ном числе 2 ре зуль та том яв ля ет ся число 29 и при этом тра ек то рия вы чис ле ний со дер жит число 14 и не со дер жит числа 25? Тра ек то рия вы чис ле ний про грам мы – это по сле до ва тель ность ре зуль та тов вы пол не ния всех ко манд про грам мы. На при мер, для про грам мы 121 при ис ход ном числе 7 тра ек то рия будет со сто ять из чисел 8, 16, 17. По яс не ние. Для сло же ния спра вед лив пе ре ме сти тель ный (ком му та тив ный) закон, зна чит, по ря док ко манд в про грам ме не имеет зна че ния для ре зуль та та. Все ко ман ды уве ли чи ва ют ис ход ное число, по это му ко ли че ство ко манд не может пре вос хо дить (30 − 21) = 9. При этом ми ни маль ное ко ли че ство ко манд — 3. Таким об ра зом, ко манд может быть 3, 4, 5, 6, 7, 8 или 9. По это му по ря док ко манд не имеет зна че ния, каж до му числу ко манд со от вет ству ет один набор ко манд, ко то рые можно рас по ло жить в любом по ряд ке. Рас смот рим все воз мож ные на бо ры и вы чис лим ко ли че ство ва ри ан тов рас спо ло же ния ко манд в них. Набор 133 имеет 3 воз мож ных ва ри антов рас по ло же ния. На бо р 1223 — 12 воз мож ных ва ри ан тов рас по ло же ния: это число пе ре ста но вок с по вто ре ни я ми (1+2+1)!/(1! · 2! · 1!)). Набор 12222 — 5 ва ри ан тов. Набор 111222 — 20 воз мож ных ва ри ан тов. Набор 11123 — 20 ва ри ан тов. Набор 111113 — 6 ва ри ан тов, набор 1111122 — 21 ва ри ан т, набор 11111112 — 8 ва ри ан тов, набор 111111111 — один ва ри ант. Всего имеем 3 + 12 + 5 + 20 + 20 + 6 + 21 + 8 + 1 = 96 про грамм. Ответ: 96. Ответ: 96. Ответ: 13 23. За да ние Сколь ко су ще ству ет раз лич ных на бо ров зна че ний ло ги че ских пе ре мен ныхx1, x2, ... x9, y1, y2, ... y9, ко то рые удо вле тво ря ют всем пе ре чис лен ным ниже усло ви ям? (¬ (x1 ≡ y1)) ≡ (x2 ≡ y2) (¬ (x2 ≡ y2)) ≡ (x3 ≡ y3) … (¬ (x8 ≡ y8)) ≡ (x9 ≡ y9) В от ве те не нужно пе ре чис лять все раз лич ные на бо ры зна че ний пе ре мен ных x1, x2, ... x9, y1, y2, ... y9, при ко то рых вы пол не на дан ная си сте ма ра венств. В ка че стве от ве та Вам нужно ука зать ко ли че ство таких на бо ров. По яс не ние. Из по след не го урав не ния на хо дим, что воз мож ны три ва ри ан та зна че ний x8 и y8: 01, 00, 11. По стро им древо ва ри ан тов для пер вой и вто рой пар зна че ний. 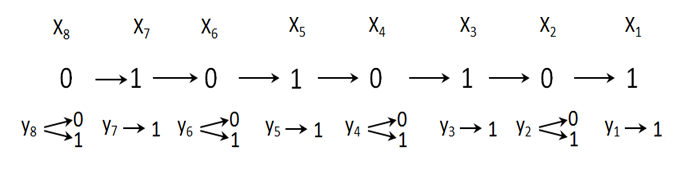 Таким об ра зом, имеем 16 на бо ров пе ре мен ных. Де ре во ва ри ан тов для пары зна че ний 11: 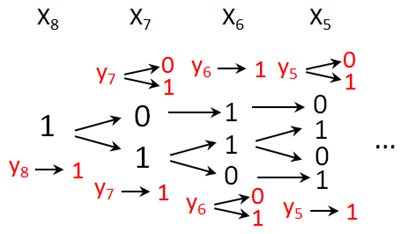 По лу ча ем 45 ва ри ан тов. Таким об ра зом, си сте ма будет иметь 45 + 16 = 61 раз лич ных на бо ров ре ше ний. Ответ: 61. Ответ: 1024 24. За да ние На об ра бот ку по сту па ет по ло жи тель ное целое число, не пре вы ша ю щее 109. Нужно на пи сать про грам му, ко то рая вы во дит на экран сумму цифр этого числа, мень ших 7. Если в числе нет цифр, мень ших 7, тре бу ет ся на экран вы ве сти 0. Про грам мист на пи сал про грам му не пра виль но. Ниже эта про грам ма для Ва ше го удоб ства при ве де на на пяти язы ках про грам ми ро ва ния.
По сле до ва тель но вы пол ни те сле ду ю щее. 1. На пи ши те, что вы ве дет эта про грам ма при вводе числа 456. 2. При ве ди те при мер та ко го трёхзнач но го числа, при вводе ко то ро го про грам ма выдаёт вер ный ответ. 3. Най ди те все ошиб ки в этой про грам ме (их может быть одна или не сколь ко). Из вест но, что каж дая ошиб ка за тра ги ва ет толь ко одну стро ку и может быть ис прав ле на без из ме не ния дру гих строк. Для каж дой ошиб ки: 1) вы пи ши те стро ку, в ко то рой сде ла на ошиб ка; 2) ука жи те, как ис пра вить ошиб ку, т.е. при ве ди те пра виль ный ва ри ант стро ки. До ста точ но ука зать ошиб ки и спо соб их ис прав ле ния для од но го языка про грам ми ро ва ния. Об ра ти те вни ма ние, что тре бу ет ся найти ошиб ки в име ю щей ся про грам ме, а не на пи сать свою, воз мож но, ис поль зу ю щую дру гой ал го ритм ре ше ния. Ис прав ле ние ошиб ки долж но за тра ги вать толь ко стро ку, в ко то рой на хо дит ся ошиб ка. По яс не ние. Ре ше ние ис поль зу ет за пись про грам мы на Пас ка ле. До пус ка ет ся ис поль зо ва ние про грам мы на любом из четырёх дру гих язы ков. 1. Про грам ма вы ве дет число 4. 2. При мер числа, при вводе ко то ро го про грам ма выдаёт вер ный ответ: 835. За ме ча ние для про ве ря ю ще го. Про грам ма ра бо та ет не пра виль но из-за не вер ной вы во ди мой на экран пе ре мен ной и не вер но го уве ли че ния суммы. Со от вет ствен но, про грам ма будет ра бо тать верно, если в числе стар шая цифра (край няя левая) равна сумме цифр, мень ших 7. 3. В про грам ме есть две ошиб ки. Пер вая ошиб ка. Не вер ное уве ли че ние суммы. Стро ка с ошиб кой: sum := sum + 1; Вер ное ис прав ле ние: sum := sum + digit; Вто рая ошиб ка. Не вер ный вывод от ве та на экран. Стро ка с ошиб кой: writeln(digit) Вер ное ис прав ле ние: writeln(sum) 25. За да ние Дан це ло чис лен ный мас сив из 20 эле мен тов. Эле мен ты мас си ва могут при ни мать целые зна че ния от –10 000 до 10 000 вклю чи тель но. Опи ши те на есте ствен ном языке или на одном из язы ков про грам ми ро ва ния ал го ритм, поз во ля ю щий найти и вы ве сти ко ли че ство пар эле мен тов мас си ва, в ко то рых хотя бы одно число де лит ся на 3. В дан ной за да че под парой под ра зу ме ва ет ся два под ряд иду щих эле мен та мас си ва. На при мер, для мас си ва из пяти эле мен тов: 6; 2; 9; –3; 6 – ответ: 4. Ис ход ные дан ные объ яв ле ны так, как по ка за но ниже на при ме рах для не ко то рых язы ков про грам ми ро ва ния и есте ствен но го языка. За пре ща ет ся ис поль зо вать пе ре мен ные, не опи сан ные ниже, но раз ре ша ет ся не ис поль зо вать не ко то рые из опи сан ных пе ре мен ных.
В ка че стве от ве та Вам не об хо ди мо при ве сти фраг мент про грам мы (или опи са ние ал го рит ма на есте ствен ном языке), ко то рый дол жен на хо дить ся на месте мно го то чия. Вы мо же те за пи сать ре ше ние также на дру гом языке про грам ми ро ва ния (ука жи те на зва ние и ис поль зу е мую вер сию языка про грам ми ро ва ния, на при мер Free Pascal 2.6) или в виде блок-схемы. В этом слу чае Вы долж ны ис поль зо вать те же самые ис ход ные дан ные и пе ре мен ные, какие были пред ло же ны в усло вии (на при мер, в об раз це, за пи сан ном на есте ствен ном языке). По яс не ние.
26. За да ние Два иг ро ка, Петя и Ваня, иг ра ют в сле ду ю щую игру. Перед иг ро ка ми лежат две кучи кам ней. Иг ро ки ходят по оче ре ди, пер вый ход де ла ет Петя. За один ход игрок может до ба вить в одну из куч (по сво е му вы бо ру) один ка мень или уве ли чить ко ли че ство кам ней в куче в два раза. На при мер, пусть в одной куче 10 кам ней, а в дру гой 7 кам ней; такую по зи цию в игре будем обо зна чать (10, 7). Тогда за один ход можно по лу чить любую из четырёх по зи ций: (11, 7), (20, 7), (10, 8), (10, 14). Для того чтобы де лать ходы, у каж до го иг ро ка есть не огра ни чен ное ко ли че ство кам ней. Игра за вер ша ет ся в тот мо мент, когда сум мар ное ко ли че ство кам ней в кучах ста но вит ся не менее 73. По бе ди те лем счи та ет ся игрок, сде лав ший по след ний ход, т.е. пер вым по лу чив ший такую по зи цию, что в кучах всего будет 73 камня или боль ше. Будем го во рить, что игрок имеет вы иг рыш ную стра те гию, если он может вы иг рать при любых ходах про тив ни ка. Опи сать стра те гию иг ро ка – зна чит опи сать, какой ход он дол жен сде лать в любой си ту а ции, ко то рая ему может встре тить ся при раз лич ной игре про тив ни ка. На при мер, при на чаль ных по зи ци ях (6, 34), (7, 33), (9, 32) вы иг рыш ная стра те гия есть у Пети. Чтобы вы иг рать, ему до ста точ но удво ить ко ли че ство кам ней во вто рой куче. | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||