Муниципальное общеобразовательное учреждение «Харламовская средняя общеобразовательная школа» Омская область Таврический район с. Харламово
 Скачать 130.74 Kb. Скачать 130.74 Kb.
|
 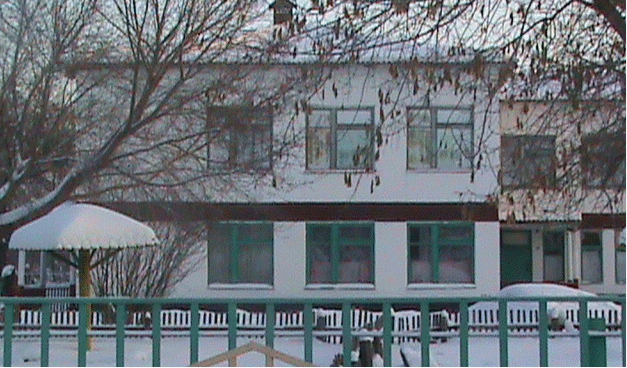       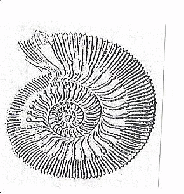 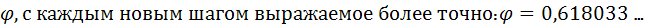 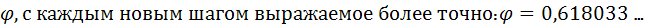       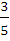 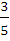 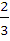 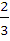    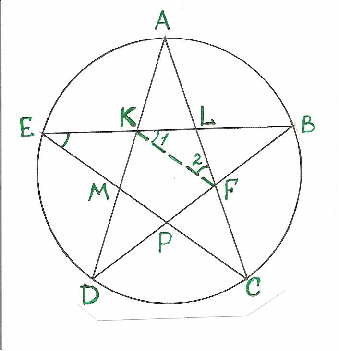 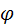 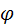   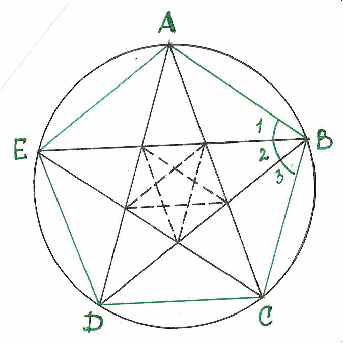   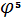 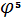   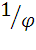 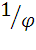 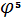 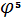   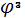 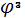 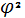 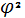 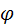    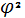 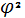 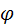   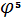 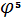 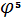 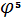   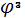 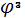 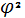 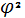 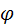 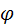 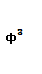 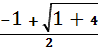 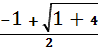 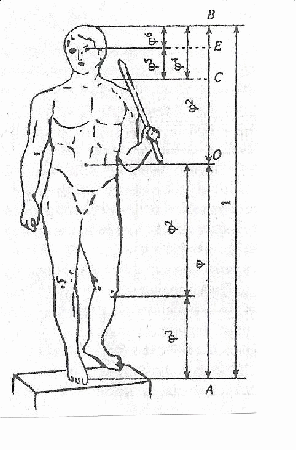   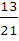 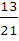   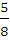 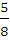 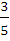 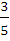   Муниципальное общеобразовательное учреждение Муниципальное общеобразовательное учреждение«Харламовская средняя общеобразовательная школа» Омская область Таврический район с. Харламово НОУ «Поиск» «Золотое сечение» Секция: математика Выполнила: Ситнова Ольга ученица 9 класса Руководитель: Баранова Татьяна Алексеевна учитель математики МОУ«Харламовская СОШ» Таврического района Омской области с. Харламово 2009 г. Содержание I. Введение---------------------------------------------------------стр. 2 II. Цель и задачи--------------------------------------------------стр. 3 III. Немного истории--------------------------------------------стр. 4-5 IV. «Золотое сечение» в Древней Греции----------------стр.6-10 V. «Золотое сечение» и «золотая спираль» в природе—--------------------------------------------------------------------------------стр11-13 VI. «Золотое сечение» в архитектуре с. Харламово----стр14-16 VII. Заключение----------------------------------------------------стр. 17 VIII. Литература--------------------------------------------------стр. 18 - 1 -I. Введение. Я занялась подробным изучением темы «Золотое сечение» после того, как однажды на уроках геометрии услышала о широком применении «золотого сечения» в архитектуре. Я рассмотрела различные энциклопедические сведения, разработки ученых, занимавшихся темой «Золотое сечение». Для нахождения материала для своей работы использовала энциклопедические справочники по математике, учебники по геометрии, учебные пособия. «Золотое сечение» в крайнем и среднем отношении - деление отрезка АВ на две части таким образом, что большая часть АС является средней пропорциональной между всем отрезком АВ и меньшей его частью СВ(золотое сечение – это деление отрезка на две части таким образом, что большая часть относится к меньшей как весь отрезок относится к большей части). Алгебраическое построение «золотого сечения» АВ = а сводится к решению уравнения a : x = x : (a-x), (где x = АС), откуда х = (√5 – 1)а / 2 = 0,62а. Отношение x к а может быть также выражено приближенно дробями , , , , ,… , где 2, 3, 5, 8, 13, 21,… - Фибоначчи числа. Геометрическое построение «золотого сечения» отрезка АВ осуществляется так: в точке В восстанавливают перпендикуляр к АВ, на нём откладывают отрезок ВЕ= ½ АВ, соединяют А и Е, откладывают ED= EB и, наконец, АС= AD, тогда будет АВ : АС = АС : СВ. АВ = а, АС = х, ВС = а – х - 2 -II. Цели и задачи научной работы. Цель работы - воспользовавшись различной литературой по геометрии, черчению, различными справочным материалами для подробного изучения темы «Золотое сечение», дать наиболее полное представление о данной теме; рассмотреть применение «золотого сечения» в архитектуре своего родного села Харламово. Задачи научной работы: 1. Ввести понятие «золотое сечение» (немного об истории). Алгебраическое нахождение «золотого сечения», геометрическое построение «золотого сечения». 2. Рассмотреть применение «золотого сечения» в искусстве Древней Греции. 3. Продемонстрировать и разобрать понятие золотой спирали в живой природе. 4. Показать применение «золотого сечения» в эпоху Возрождения 5.Частично изучив архитектуру своего села, указать здания с применением золотого сечения. - 3 – III. Немного истории… В дошедшей до нас античной литературе «золотое сечение» впервые встречается во II книге «Начал» Евклида, где даётся геометрическое построение, равносильное решению квадратного уравнения вида x(a+x) = а². Евклид применял «золотое сечение» при построении правильных 5- и 10-угольников, а также в стереометрии при построении правильных 12- 20-гранников. Несомненно, что «золотое сечение» было известно и до Евклида. Весьма вероятно, что задача «золотого сечения» была решена ещё пифагорейцами, которым приписывают построение правильного треугольника и геометрического построения, равносильные решению квадратных уравнений. Именно пентаграмму Пифагорейцы выбрали символом своего союза - религиозной секты во главе с Пифагором (ок. 580-500 до н. э.), которая проповедовала братскую любовь к друг другу, отречение от внешнего мира, общность имущества и т. д. Пифагорейцев отличала от других то, что они считали возможным добиться очищения духа при помощи математики. По их теории, в основу мирового порядка положены числа. Мир, считали они, состоит из противоположностей к единству. Гармония же заключена в числовых отношениях. Пифагорейцы приписывали числам различные свойства. Так, чётные числа называли женскими, нечётные (кроме 1) – мужскими. Число 5 – как сумма первого женского числа 2 и первого мужского числа 3 – считалось символом любви. Отсюда такое внимание к пентаграмме, имеющей 5 углов. После Евклида исследованием «золотого сечения» занимались Гипсикл (II в. до н.э.), Папп Александрийский (III в. до н.э.) и др. В средневековой Европе с «золотым сечением» познакомились по арабским переводам «Начал» Евклида. Переводчик и комментатор Евклида Дж. Кампано из Новары (XIII в.) добавил к 13 книге «Начал» предположение, содержащее арифметическое доказательство несоизмеримости отрезка и обеих частей его «золотого сечения». В 15-16 вв. усилился интерес к «золотому сечению» среди учёных и художников в связи с его применением, как в геометрии, - 4 - так и в искусстве, особенно в архитектуре. В средние века считалось, что пентаграмма служит охранным знаком от сатаны. Вспомним, например, как описывал Гёте проникновение дьявола Мефистофеля в келью доктора Фауста, на которой была начертана пентаграмма. Мефистофель сначала позвал чёрного пуделя отгрызть кончик двери с частью пентаграммы. Только после этого он сам смог предстать перед Фаустом. Л. Пачоли посвятил «золотому сечению» трактат «О божественной пропорции» (1509); о «золотом сечении» много писал в одном из своих ранних произведений И. Кеплер. Леонардо да Винчи считал, что идеальные пропорции человеческого тела должны быть связаны с числом Ф, деление отрезка в отношении Ф он назвал «золотым сечением». «Золотое сечение» или близкие ему пропорциональные отношения легли в основу композиционного построения многих произведений мирового искусства, например, Капелла Пации во Флоренции, архитектора Ф. Брунеллески, XV в. - 5 - IV. «Золотое сечение» и законы искусства в Древней Греции. Статуя «Дорифор». Рассмотрим теперь применение «золотого сечения» в скульптурах Древней Греции. Работы Фидия в оригиналах почти не сохранились, поэтому для иллюстрации возьмём произведение его младшего современника, скульптора и теоретика искусства Поликлета (вторая половина V в. до н. э.). В своём трактате «Канон» он стремился установить законы пропорциональности человеческого тела. Теория пропорций Поликлета ярко воплотилась в статуе «Дорифор» - копьеносец, которую он изваял в строгом соответствии всех частей. В этой статуе мы встречаем много раз применённое число. Так, пупок (точка О) делит высоту статуи в отношении «золотого сечения». Значит, если высоту АВ принять за 1, то АО = φ, но тогда ОВ = 1 - φ. Однако на рисунке показано, что расстояние ОВ берётся равным. Нет ли здесь противоречия? Проверим: если считать, что 1-φ= φ, то приходим к уравнению φ² - 6 - + φ - 1= 0. Откуда φ =, т.е. получили то же самое значение, которое вычислили ранее. Но проанализируем другие пропорции знаменитой статуи. Расстояние от подошвы копьеносца до его колена равно φ³, высота шеи вместе с головой равна φ , длина шеи до уха -φ, а расстояние уха до макушки -φ. Таким образом, в этой статуе мы видим геометрическую прогрессию со знаменателем ,,,,, . «Золотое сечение» многократно встречается при анализе соразмерностей Парфенона. Это древнее сооружение с его гармоническими пропорциями дарит нам такое же эстетическое наслаждение, как и нашим предкам. Многие искусствоведы, стремившиеся раскрыть секрет того могучего эмоционального воздействия, которое это здание оказывает на зрителя, искали и находили в соотношениях его частей золотую пропорцию. - 7 - Известен целый ряд пропорций. Так, приняв за ширину торцевого здания, можно получить геометрическую прогрессию, состоящую из восьми членов: расстояние между второй и седьмой колоннами равно , между третьей и шестой , между четвёртой и пятой - . Аналогичные закономерности мы видим и в построении здания по высоте. Объединив их, получаем прогрессию: 1, ,,,,. Здесь поучительно вспомнить о пропорциях тела, отмеченных заранее. Сравнивая, видим, что отношение торцевой длины здания к его высоте равно отношению человеческого роста к длине нижней части тела: . Высота крыши Парфенона относится к расстоянию между крышей и капителями колонн, как :, т.е. так же, как отрезок ВС относится к отрезку ЕС. Эти совпадения не случайны. В своих архитектурных творениях древнегреческие мастера исходили из пропорций, которые видели в природе, и прежде всего в пропорциях человеческого тела. Чем же интересен этот символ с точки зрения математики? Построим сначала правильный пятиугольник. Это легко сделать с помощью описанной окружности. Из её центра надо последовательно отложить углы с вершиной в центре окружности, равные = 72°, стороны углов пересекут окружность в точках А, В, С, D, Е. Соединив их последовательно, получим правильный пятиугольник. А теперь проведём в этом пятиугольнике все диагонали. Они образуют правильный звездчатый пятиугольник, т.е. знаменитую пентаграмму. - 8 - Интересно, что стороны пентаграммы, пересекаясь, образуют снова правильный пятиугольник, в котором пересечение диагоналей даёт нам новую пентаграмму, а в пересечении её сторон мы снова видим правильный пятиугольник, открывающий возможность построения новой пентаграммы. И так далее до бесконечности. Пентаграмма представляет собой вместилище «золотых пропорций». При n = 5 имеем 180°·3:5= 108°. В пятиугольнике ABCDE, ے 1 = 108°:3= 36°. Теперь рассмотрим пентаграмму на рисунке. Соединим в ней точки K и F. Выше уже отмечалось, что пятиугольник KLFPM- правильный, т.е. угол KLF=108°. Тогда ے 1= ے 2 =36°. Но угол Е тоже равен 36°. Из того что 1=Е, следует, что ЕС параллельна KF, а тогда ∆ BEP ~ ∆ BKF, EB:KB=PD: FB. Обозначим ЕВ = а, КВ = х, перепишем пропорцию иначе: а: х= х (а-х), или х² +ах - а² = 0. Мы получили то же самое уравнение, решением которого является х = ·а. - 9 - Значит, КВ: ЕВ = Таким образом доказано, что стороны пентаграммы, пересекаясь, делят друг друга на отрезки, длины, которых образуют «золотую пропорцию». - 10 - V. «Золотое сечение» и «золотая спираль» в живой природе. Красота природных форм рождается во взаимодействии двух физических сил - тяготения и инерции. «Золотая пропорция»- символ этого взаимодействия, поскольку диктуемое ею отношение большей части целого к самому целому выражает основные моменты живого роста: стремительный рост юного побега до зрелости и замедлённый рост «по инерции» до момента цветения, когда достигшее полной силы растение готовится дать жизнь новому побегу. Рассматривая расположение листьев на стебле растений можно заметить, что между каждыми двумя парами листьев (А и С) третья пара расположена в месте золотого сечения (В). - 11 - Одним из первых проявления «золотого сечения» в природе подметил разносторонний наблюдатель, автор многих смелых гипотез немецкий математик и астроном Иоганн Кеплер(1571-1630). С 17 века наблюдение математических закономерностей в ботанике и зоологии стали быстро накапливаться. Рассмотрим расположение семечек в корзинке подсолнуха. Они выстраиваются вдоль спиралей, которые закручиваются как слева на право, так и справа налево. В одну сторону закручено 13 спиралей, в другую 21. В более крупных соцветиях подсолнечника число соответствующих спиралей 21 и 34, 34 и 55. Похожее спиральное расположение наблюдается у чешуек сосновых шишек или ячеек ананаса. В верхушках многих побегов можно различить такие же системы спиральных рядов. Число рядов листьев или цветков, ориентированных противоположно, отличается у разных растений, но чаще всего принимает следующие значения: = 0,5, = 0,666…, =0,6, =0,615…, Начиная со второго члена этого ряда повторяется число Логарифмическая спираль единственная из спиралей не меняет своей формы при увеличении размеров. Видимо, это свойство и послужило причиной того, что в живой природе логарифмическая спираль встречается чаще других. По логарифмической спирали свёрнуты раковины многих улиток и моллюсков; та же спираль встречается в соцветиях растений; даже пауки, сплетая паутины, закручивают нити вокруг центра по логарифмической спирали. - 12 - Таким образом, человеческие построения о красивом формируется явно под влиянием того, какие воплощения порядка и гармонии человек видит в живой природе. А природа, как известно, любит повторения. В различных своих творениях, казалось бы, очень далеких друг от друга, она может использовать одни и те же принципы. «Золотое сечение»- один из этих основополагающих принципов природы. - 13 - VI. «Золотое сечение» в архитектуре села Харламово С помощью данных фотографий, произведя ряд вычислений, я выяснила, что фасадная часть зданий № 1, № 2, № 3, № 7 действительно построена по принципу «золотого сечения». № 1 № 2 - 14 - №3 № 4 - 15 – № 5 № 6 № 7 - 16 – VII. Заключение. В своей научной работе «Золотое сечение» я подробно изучила данную тему. Рассмотрела, как применялось «золотое сечение» в эпоху Возрождения и в искусстве Древней Греции. Научилась выполнять алгебраическое нахождение «золотого сечения» и геометрическое построение «золотого сечения». Разобрала и продемонстрировала понятия «золотого сечения», «золотой спирали» в живой природе. Частично изучив архитектуру своего села, произведя вычисления по фотографиям, я нашла в архитектуре села дома, построенные с применением «золотого сечения». Я сделала вывод, что в отличии от архитектуры Древней Греции, в современной архитектуре «золотое сечение» найти трудно, т.к. архитекторы и строители не предусматривают цели красоты и гармонии, им важно чтобы здание возвели быстро из готовых конструкций, затратив как можно меньше средств. А ведь непременным условием правильного и красивого изображения предмета служит соблюдение определенных соотношений между размерами отдельных частей растений, скульптуры, здания. Такая исследовательская работа мне нравится. Я считаю, что материал, изложенный в моей научной работе, будет полезен для работы на дополнительных занятиях по математике и математических кружках. - 17 - VII. Литература.
- 18 - |