Формула корней квадратного уравнения
 Скачать 41.76 Kb.
|
| Урок математики в 8 классе на тему: «Формула корней квадратного уравнения» Учитель математики МКОУ Перлевской СОШ Семилукского района Воронежской области Сомова О.В. Цели и задачи урока: -обучающие: познакомить с формулой корней квадратного уравнения, дискриминанта, учить применять эти формулы, рассмотреть приемы решения уравнений; -развивающие: развивать логическое мышление учащихся, повышать интерес к изучаемой теме; -воспитательные: воспитать стремление к достижению цели, воспитание интереса к математике. Тип урока: Урок изучения нового материала Оборудование урока: Мультимедийный проектор, презентация. Ход урока
Сообщить тему и цели урока.
1) (слайды 2-6) Найди лишнее:
Проверка осуществляется с помощью компьютера (лишнее исчезает) 2)(слайд 7) Составьте квадратные уравнения, если известны их коэффициенты:
1)(слайд 8)Простые уравнения люди научились решать более трех тысяч лет назад в Древнем Египте, Вавилоне и только 40 лет назад научились решать квадратные уравнения. Одним из тех, кто внес большой вклад в развития математики, был французский математик Виет. 2)(слайды 9-13)Вывод формул корней квадратного уравнения. Опр. Дискриминантом квадратного уравнения ах2 + bх + с = 0 называется выражение b2 – 4ac. Его обозначают буквой D, т.е. D= b2 – 4ac. Возможны три случая:
Если D 0 В  этом случае уравнение ах2 + bх + с = 0 имеет два действительных корня: Если D = 0 В этом случае уравнение ах2 + bх + с = 0 имеет один действительный корень: 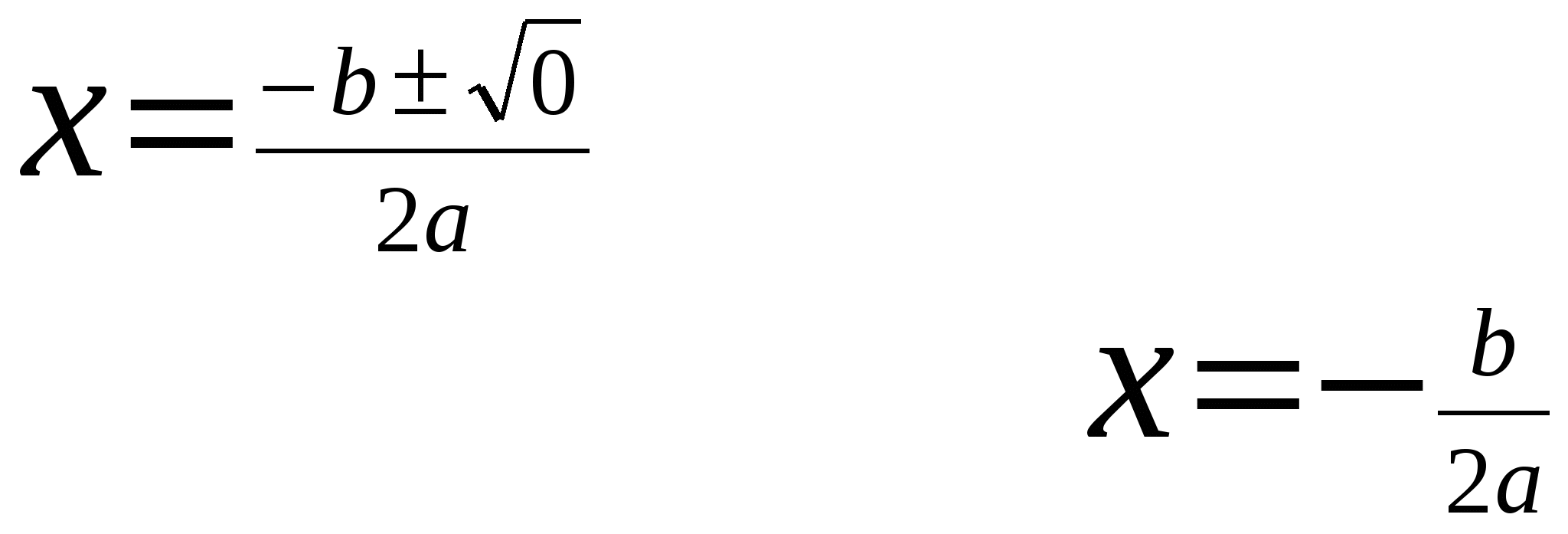 Если D 0 Уравнение ах2 + bх + с = 0 не имеет действительных корней. Корней нет. Обобщим. ах2 + bх + с = 0.  3)(слайд 14-17) Рассмотрим несколько примеров. Решить уравнение 2x2- 5x + 2 = 0 Здесь a = 2, b = -5, c = 2. Имеем D = b2- 4ac = (-5)2- 422 = 9. Так как D > 0, то уравнение имеет два корня. 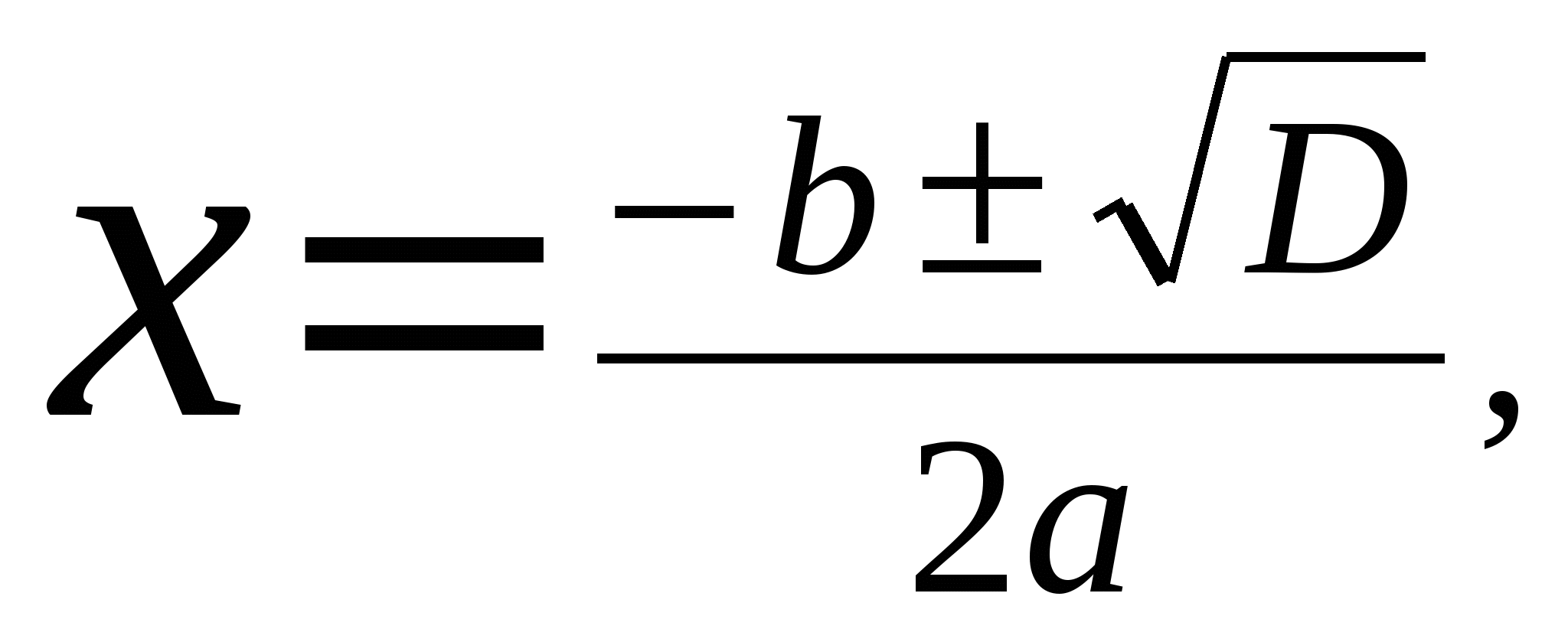 Найдем их по формуле  то есть x1 = 2 и x2 = 0,5 - корни заданного уравнения Решить уравнение 2x2- 3x + 5 = 0 Здесь a = 2, b = -3, c = 5. Найдем дискриминант D = b2- 4ac= (-3)2- 4·2·5 = -31, т.к. D < 0, то уравнение не имеет действительных корней. Решить уравнение x2- 2x + 1 = 0 Здесь a = 1, b = -2, c = 1. Получаем D = b2- 4ac = (-2)2- 4·1·1= 0, поскольку D=0 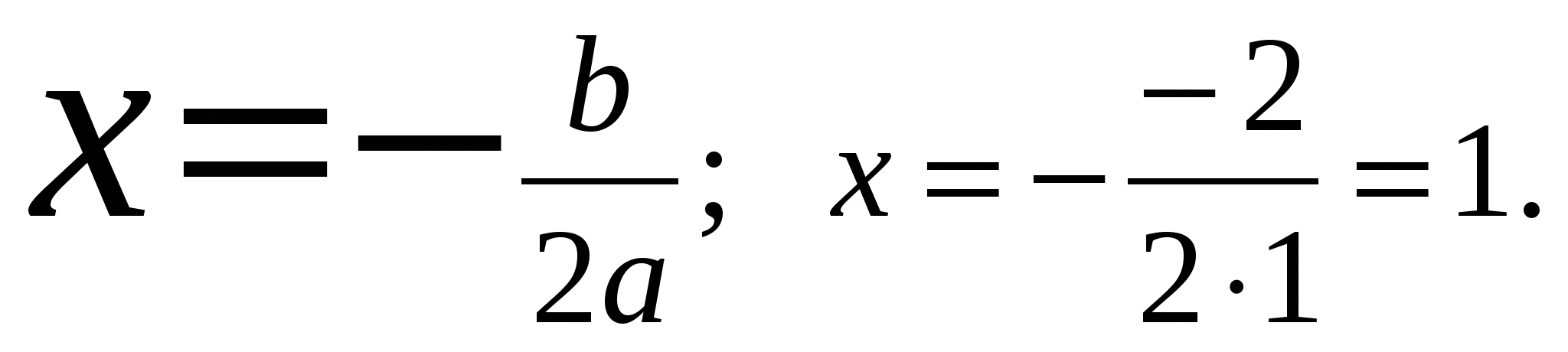 Получили один корень х = 1.
Даются задания, которые решаются на доске учениками с проверкой учителем. №1. Решите уравнения: а) х2+7х-44=0; Здесь a = 1, b = 7, c = - 44. И  меем D = b2- 4ac = (7)2- 41(-44) = 225. Так как D > 0, то уравнение имеет два корня б) 9у2+6у+1=0; Здесь a = 9, b = 6, c = 1. Получаем D = b2- 4ac = (6)2- 4·1·9= 0, поскольку D=0  в) –2t2+8t+2=0; Здесь a = -2, b = 8, c = 2. Имеем D = b2- 4ac = (8)2- 4(-2)2 = 80 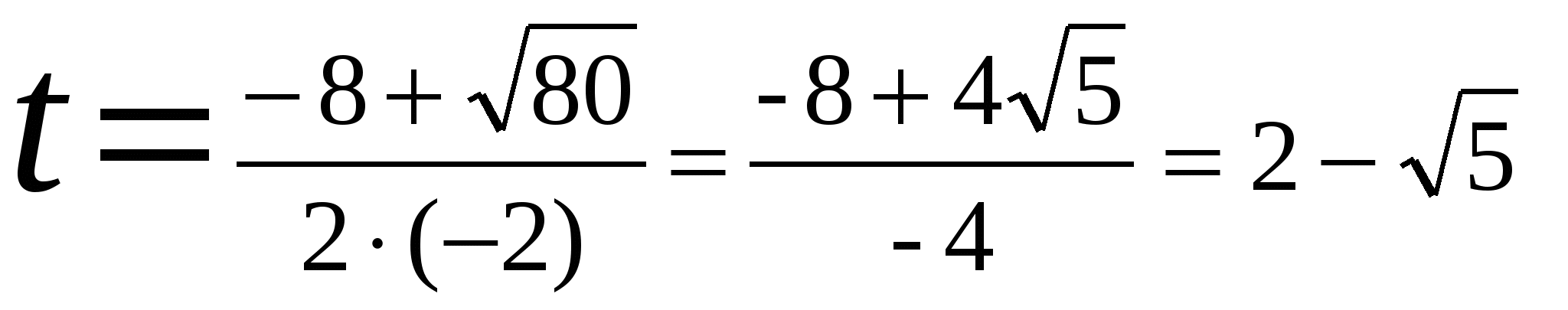  г) а+3а2= -11. а+3а2 +11=0. Здесь a = 1, b = 3, c = 11. Найдем дискриминант D = b2- 4ac= (3)2- 4·1·11 = -35, т.к. D < 0, то уравнение не имеет действительных корней. д) х2-10х-39=0; Здесь a = 1, b = -10, c = - 39. И  меем D = b2- 4ac = (-10)2- 41(-39) = 256. Так как D > 0, то уравнение имеет два корня е) 4у2-4у+1=0; Здесь a = 4, b = -4, c = 1. Получаем D = b2- 4ac = (-4)2- 4·4·1= 0, поскольку D=0  ж) –3t2-12t+6=0; Здесь a = -3, b = -12, c = 6. Имеем D = b2- 4ac = (-12)2- 4(-3)6 = 216   3) 4а2+5= а. 4а2+5 – а=0. Здесь a = 4, b = -1, c = 5. Найдем дискриминант D = b2- 4ac= (-1)2- 4·4·5 = -79, т.к. D < 0, то уравнение не имеет действительных корней. №2. а)При каких значениях х равны значения многочленов: (1-3х)(х+1) и (х-1)(х+1)? (1-3х)(х+1) = (х-1)(х+1) х-3х2+1-3х=х2-1 -4х2-2х+2=0 Здесь a = -4, b = -2, c = 2. И  меем D = b2- 4ac = (-2)2- 4(-4)2 = 36. Так как D > 0, то уравнение имеет два корня Б)При каких значениях х равны значения многочленов: (2-х)(2х+1) и (х-2)(х+2)? (2-х)(2х+1) = (х-2)(х+2) 4х+2-2х2-х=х2-4 -3х2+3х+6=0 Здесь a = -3, b = 3, c = 6. И  меем D = b2- 4ac = (3)2- 4(-3)6 = 81. Так как D > 0, то уравнение имеет два корня
| ||||||