Решение квадратных уравнений. Способы решения
 Скачать 49.92 Kb. Скачать 49.92 Kb.
|
Конспект урока в 9 классе. Алгебра. Наумова Н.И. Тема: Решение квадратных уравнений. Способы решения. Цель: 1.Актуализировать знания учащихся по изучаемой теме «Решение квадратных уравнений». 2.Содействовать формированию познавательной деятельности учащихся в обобщение способов решения квадратных уравнений. 3.Способствовать формированию умения выделить главное в изучаемой теме, наиболее общее и существенное в способах решения квадратных уравнений. 4.Содействовать умению осуществлять самоконтроль и самокоррекцию. Задачи урока: 1.Обобщить изученные способы решения квадратных уравнений. 2.Систематизировать знания учащихся в умении решать квадратные уравнения разными способами. 3.Проверить полученные знания средствами информатизации и осуществить самоконтроль. Тип урока: Урок обобщения и систематизации знаний, умений, навыков средствами информатизации. Организационный момент:
Задачи урока: Информация о квадратных уравнениях: Квадратные уравнения – это основа, фундамент, на котором покоится величественное здание – алгебра. Квадратные уравнения находят широкое применение при решении тригонометрических, показательных, логарифмических, иррациональных уравнений, с которыми вам предстоит познакомиться в старших классах. На уроке мы с вами поговорим лишь о некоторых способах решения квадратных уравнений.
Квадратное уравнение ах²+вх+с=0, а≠0, умножим обе части уравнения на 4а и имеем: 4а²х²+4авх+4ас=0 ((2ах)²+2ах2в+в²)-в²+4ас=0 (2ах+в)²= в²-4ас 2ах+с=±√ в²-4ас 2ах=-в±√ в²-4ас х= -в±√ в²-4ас 2а ; в²-4ас=D – дискриминант. 2) От знака дискриминанта D зависит количество корней. D > 0, - 2 корня D = 0, - 1 корень D < 0, - корней нет. 3) А теперь проверим свои знания в решении уравнений. Решим уравнения: Варианты ответов: а) 4х²+7х+3=0, а) -¾; -1; б) 1; ¾; в) 4; 3 б) 4х²+20х+25=0, а) 0; 5; б) -2,5; в) корней нет в) х²-6х-40=0 а) 8; 5; б) 5,6; в) -4; 10. 4) Проверь себя: а) верно; б) подумай; в) торопишься; а) подумай; б) верно; в) торопишься; а) торопишься; б) подумай; в) верно. 5. 1) Решение уравнений с использованием теоремы Виета. Как известно, приведенное квадратное уравнение имеет вид х²+рх+q=0, его корни удовлетворяют теореме Виета, которая при а=1 имеет вид х1х2=q, х1+х2= -р. 2) По коэффициентам р и q можно определить знаки корней. а) Если q > 0, то уравнение имеет 2 одинаковых по знаку корня и это зависит от коэффициента р. Если р > 0, то оба корня отрицательны: х²+8х+7=0, т.к. р=8, q=7, то х1= -7; х2= -1. Если р< 0, то оба корня положительны: х²-3х+2=0, т.к. р= -3, q=2, то х1=1, х2=2. б) Если q < 0, то уравнение имеет два разных по знаку корня, причем больший по модулю корень имеет положительный знак, если р < 0, х²-8х-9=0, т.к. р= -8, q= -9, то х1=9, х2= -1, и отрицательный знак, если р > 0, х²+4х-5=0, т.к. р=4, q= -5, то х1= -5, х2=1. 3) Не решая уравнения, определить знаки его корней. /Устная работа/ 1) х²-2х-15=0, 1) (+; -) (5; -3) 2) х²+2х-8=0, 2) (+; -) ( -4;2) 3) х²-12х+35=0, 3) (+;+) (5;7) 4) 3х²+14х+16=0, 4) ( -; -) 5) х²-5х+6=0, 5) (+;+) (2;3) 6) х²-2х+1=0, 6) (+;+) (1) 6. Следующий способ: Разложение квадратного уравнения на множители по формуле а(х-х1)(х-х2), где х1 и х2 - корни а) х²+10х-24=0, х²+12х-2х-24=х(х+12)-2(х+12)=(х-2)(х+12)=0 => х1=2, х2= -12 б)6х²+х2=0 6х²+х2=6х²+4х-3х-²2=(6х²-3х)+(4х-2)=3х(2х-1)+2(2х-1)=(2х-1)(3х+2)=0 =>х1=1/2; х2=-2/3. 7.Самостоятельная работа/выполнение в тетради с последующей взаимопроверкой/. Разложить на множители. 4х²+7х-2=0 х²-4х+4=0 х²+2х-8=0 х²+4х+4=0 х²-3х=0 6х²-7х+2=0 х²-81=0 х²-3х+2=0. 8.Метод выделения полного квадрата. Уравнение х²+6х-7=0 решим ,выделив полный квадрат. х²+6х-7=х²+2х3+9-9-7=(х+3)-16=0 т.е. (х+3)=16 х+3=4 или х+3=-4 х1=1 х2=-7. 9.Графический способ решения квадратных уравнений. 1.Приведённое квадратное уравнение х²+рх+g=0 2.Перепишем его так: х²=-рх-g. 3.Построим графики зависимости у=х² и у=-рх-g. 4.График первой зависимости – парабола. 5.График второй зависимости – прямая. 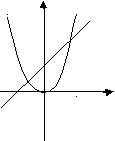 6.Найдём точки пересечения параболы и прямой. Абсциссы точек пересечения 6.Найдём точки пересечения параболы и прямой. Абсциссы точек пересечения являются корнями квадратного уравнения. Решим графически уравнение :4х²-12х-8=0. Построим параболу у=х² и прямую у=3х+2. 10.Решим графически уравнение х²-2х-3=0 х²=2х+3 ,у=х²-парабола, у=2х+3- прямая. Строим прямую по двум точкам: А(-1,5;0) и В(0;3). Парабола и прямая пересекутся в 2 точках с абсциссами х1=-1 и х2=3. /Графики представлены для рассмотрения./ 11. Какова же связь квадратичной функции и квадратного уравнения? Квадратичная функция. Решая квадратное уравнение, мы находим нули функции ,т.е. квадратичную функцию приравниваем 0 и решаем уравнение f(х)=0. Действительно, корни этого уравнения являются нулями функции у=f(х). 12. Определить нули функции, если они есть: у=х²+4х-5. У=0; х²+4х-5=0. Строим график функции и определяем абсциссы точек, в которых график этой функции либо пересекут ось абсцисс, либо касается её, либо не имеет общих точек. При определении нулей функции в первую очередь определяем знак D и знак коэффициента а. 13.Тестовое задание: Определись в своих знаниях и проверь свои умения. Какой из приведённых на рисунке графиков квадратичной функции у=ах²+вх+с соответствует данному условию: 1)D >0, а > 0
4) D<0, а < 0 5)D=0, а > 0. /Даны графики функций / Верные варианты ответов: 1(1), 2(5), 3(6), 4(2), 5(4). /Инструкция по самооценке: подсчитать верные ответы без ошибок-5, с 1 ошибкой -4, и т. д./ 14.Задание на дом: № 163, 187, 188. 15.Заключение: Знание способов решения квадратных уравнений и умение работать с графиками поможет нам в дальнейшем при решении неравенств второй степени с одной переменной и решение систем квадратных уравнений. Рефлексия: Чем мы занимались на уроке? Что нового узнали? Что вам понравилось? Что полезное возьмёте себе на вооружение при дальнейшем изучении тем, связанных с функциями и уравнениями? 16.Итог урока. |