|
В – 1
Назовите углы треугольника ДЕК, прилежащие к стороне КЕ: __________
Назовите угол треугольника MNP, заключённый между сторонами NP и PM: ________
Медиана в равнобедренном треугольнике является его биссектрисой и высотой. Это утверждение:
а) всегда верно; б) может быть верно; в) всегда неверно.
Если треугольник равносторонний, то:
а) он равнобедренный; б) все его углы равны; в) любая его высота является
биссектрисой и медианой.
В каком треугольнике только одна его высота делит треугольник на два равных треугольника?
а) в любом; б) в равнобедренном; в) в равностороннем.
Биссектриса в равностороннем треугольнике является медианой и высотой. Это утверждение:
а) всегда верно; б) может быть верно; в) всегда неверно.
Если треугольник равнобедренный, то:
а) он равносторонний;
б) любая его медиана является биссектрисой и высотой;
в) ответы а) и б) неверны.
В каком треугольнике любая его высота делит треугольник на два равных треугольника?
а) в любом; б) в равнобедренном; в) в равностороннем.
Подчеркнуть нужные слова текста в скобках:
окружность – это (абстрактная, геометрическая, плоская) фигура, состоящая из (множества, всех) точек, расположенных на (одинаковом, заданном) расстоянии от (некоторой, центральной) точки.
Закончить определение: диаметр окружности – это….
а) два радиуса, лежащие на одной прямой;
б) хорда, проходящая через центр окружности;
в) прямая, проходящая через две точки и центр окружности.
Закончить определение: дуга окружности – это …
а) часть окружности, выделенная точками;
б) часть окружности, ограниченная двумя точками;
в) часть окружности, ограниченная хордой.
На сколько дуг делят окружность две точки, лежащие на окружности:
а) на одну; б) на две; в) на три.
Как называется отрезок, соединяющий центр окружности с любой точкой окружности?
а) длина окружности; б) радиус окружности; в) половина диаметра окружности.
Сформулируйте первый признак равенства треугольников:
________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
Критерии оценок:
-
Количество верных ответов
|
Оценка
|
13-14
|
5
|
12-9
|
4
|
8-6
|
3
|
Менее 6
|
2
|
Ф.И._____________________
Проверочный тест (5-7 мин)
В – 2
Назовите углы треугольника MNP, прилежащие к стороне MN: __________
Назовите угол треугольника ДЕК, заключённый между сторонами ДЕ и ДК: ________
Если треугольник равнобедренный, то:
а) он равносторонний;
б) любая его медиана является биссектрисой и высотой;
в) ответы а) и б) неверны.
Биссектриса в равностороннем треугольнике является медианой и высотой. Это утверждение:
а) всегда верно; б) может быть верно; в) всегда неверно.
Медиана в равнобедренном треугольнике является его биссектрисой и высотой. Это утверждение:
а) всегда верно; б) может быть верно; в) всегда неверно.
В каком треугольнике только одна его высота делит треугольник на два равных треугольника?
а) в любом; б) в равнобедренном; в) в равностороннем.
Если треугольник равносторонний, то:
а) он равнобедренный; б) все его углы равны; в) любая его высота является
биссектрисой и медианой.
В каком треугольнике любая его высота делит треугольник на два равных треугольника?
а) в любом; б) в равнобедренном; в) в равностороннем.
Подчеркнуть нужные слова текста в скобках:
радиус окружности – это (линия, прямая, отрезок) соединяющая центр окружности с (заданной, какой-либо) точкой окружности.
Закончить определение: диаметр окружности – это….
а) два радиуса, лежащие на одной прямой;
б) хорда, проходящая через центр окружности;
в) прямая, проходящая через две точки и центр окружности.
Закончить определение: центр окружности – это …
а) точка, куда ставится ножка циркуля при начертании окружности;
б) середина окружности;
в) точка, равноудалённая от всех точек окружности.
Как изображается хорда на чертеже окружности:
а) прямой линией; б) дугой окружности; в) отрезком с концами, лежащими
на окружности.
Как называется отрезок, соединяющий центр окружности с любой точкой окружности?
а) длина окружности; б) радиус окружности; в) половина диаметра окружности.
Сформулируйте второй признак равенства треугольников:
________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
Критерии оценок:
-
Количество верных ответов
|
Оценка
|
13-14
|
5
|
12-9
|
4
|
8-6
|
3
|
Менее 6
|
2
|
7. Самостоятельная работа с дифференцированными заданиями в 18 вариантах по теме «Линейная функция», алгебра, 7 класс.
7 кл С/р «Линейная функция и её график»
К- №1
1. График функции y(x) – ломаная MNPKC, где
М(-13;6), N(-7;2), P(-2;2), K(2;6), C(5;-4).
Построить этот график.
Используя график функции, найти y(x) при
х = -10; -5; 0; 3.
При каком значении х значение функции y(x) равно 4; 0; -2?
Указать три значения х, при которых
y(x) > 0, и три значения х, при которых y(x) < 0.
2. Заполнить таблицу, если y(x) = 4x – 1:
3. Построить график функции y(x) = -7x.
|
7 кл С/р «Линейная функция и её график»
К- №2
1. График функции y(x) – ломаная BCDAM, где
B(-10;4), C(-6;4), D(-4;7), A(0;2), M(6;-2).
Построить этот график.
Используя график функции, найти y(x) при
х = -8; -3; 3; 6.
При каком значении х значение функции y(x) равно 6; 1; -1?
Указать три значения х, при которых
y(x) > 0, и три значения х, при которых y(x) < 0.
2. Заполнить таблицу, если y(x) = 2x – 1:
3. Построить график функции y(x) = -3x.
|
7 кл С/р «Линейная функция и её график»
К- №3
1. График функции y(x) – ломаная MNPKCD, где
М(-7;-4), N(-7;-1), P(-3;1), K(2;1), C(6;5), D(2;5).
Построить этот график.
Используя график функции, найти y(x) при
х = -5; 0; 4.
При каком значении х значение функции y(x) равно -3; 0; 1; 4?
Указать три значения х, при которых
y(x) > 0, и три значения х, при которых y(x) < 0.
2. Заполнить таблицу, если y(x) = -7x + 1:
x
|
-2
|
1
|
8
|
-15
|
|
|
|
|
y(x)
|
|
|
|
|
-1
|
0
|
8
|
15
|
3. Построить график функции y(x) = 7x.
|
7 кл С/р «Линейная функция и её график»
К- №4
1. График функции y(x) – ломаная EFKLM, где
E(-8;2), F(-5;2), K(2;-1), L(-3;4), M(4;1).
Построить этот график.
Используя график функции, найти y(x) при
х = -6; -2; 0; 3.
При каком значении х значение функции y(x) равно 0; 1; 3?
Указать три значения х, при которых
y(x) > 0, и три значения х, при которых y(x) < 0.
2. Заполнить таблицу, если y(x) = 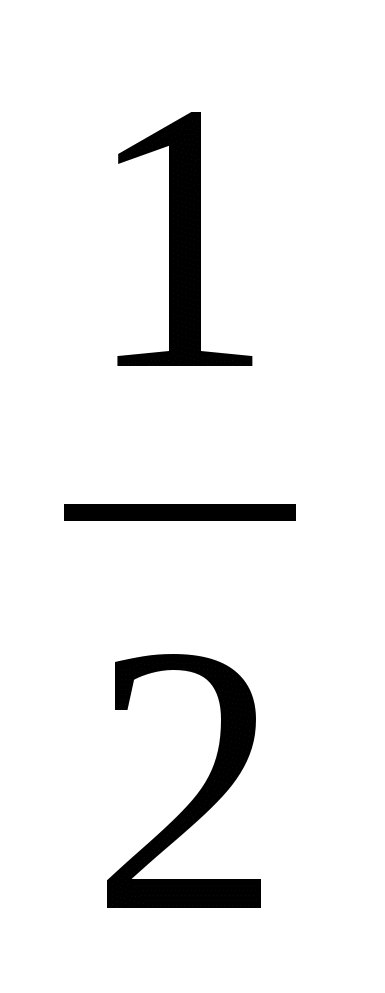 x + 3: x + 3:
3. Построить график функции y(x) = 5x.
|
7 кл С/р «Линейная функция и её график»
К- №5
1. График функции y(x) – ломаная ABCDPK, где
A(-4;9), B(0;7), C(-2;3), D(2;3), P(6;-3), K(9;-3).
Построить этот график.
Используя график функции, найти y(x) при
х = -2; 0; 4; 8.
При каком значении х значение функции y(x) равно 8; 5; -1?
Указать три значения х, при которых
y(x) > 0, и три значения х, при которых y(x) < 0.
2. Заполнить таблицу, если y(x) = 2 - 4x:
x
|
|
4
|
0
|
|
-2
|
|
|
|
y(x)
|
5
|
|
|
7
|
|
-13
|
10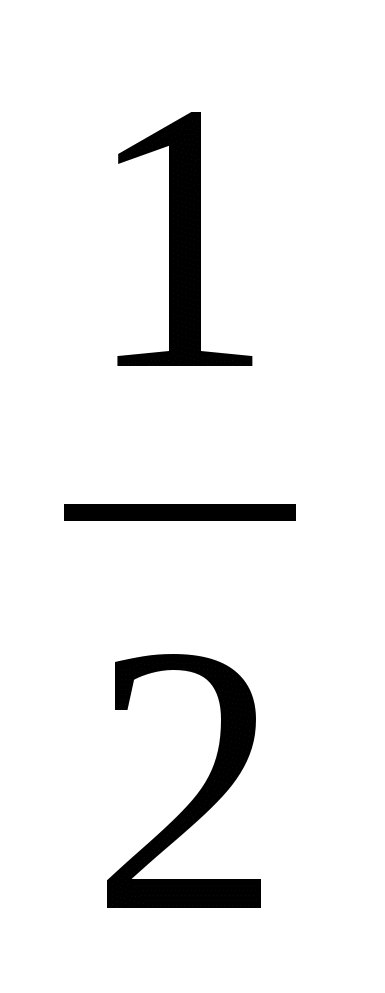
|
9
|
3. Построить график функции y(x) = 3x.
|
7 кл С/р «Линейная функция и её график»
К- №6
1. График функции y(x) – ломаная ABCEK, где
A(-4;-3), B(-2;0), C(2;0), E(5;3), K(3;5).
Построить этот график.
Используя график функции, найти y(x) при
х = -3; 0; 3;4.
При каком значении х значение функции y(x) равно -1;1; 3?
Указать три значения х, при которых
y(x) > 0, и три значения х, при которых y(x) < 0.
2. Заполнить таблицу, если y(x) = 8 - 4x:
3. Построить график функции y(x) = 3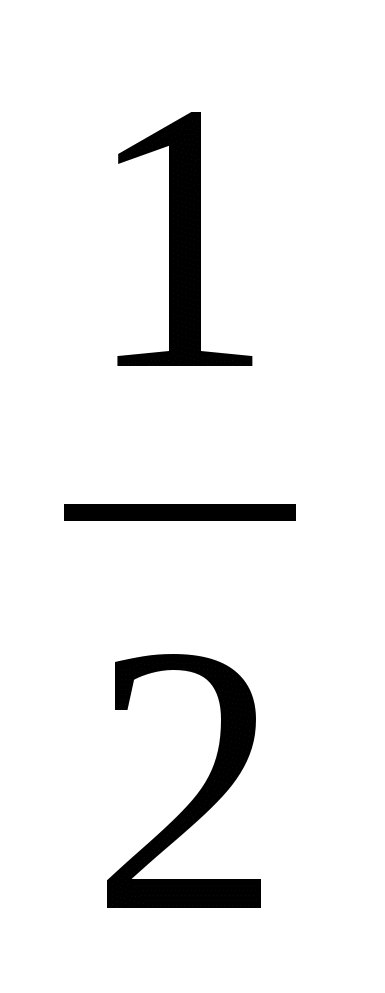 x. x.
|
7 кл С/р «Линейная функция и её график»
К- №7
1. График функции y(x) – ломаная AMPKO, где
A(-2;0), M(0;-4), P(3;-4), K(6;2), O(9;4).
Построить этот график.
Используя график функции, найти y(x) при
х = 0; -1; 2; 4; 7.
При каком значении х значение функции y(x) равно -2; 0; 1; 3?
Указать три значения х, при которых
y(x) > 0, и три значения х, при которых y(x) < 0.
2. Заполнить таблицу, если y(x) = -5 + x:
3. Построить график функции y(x) = -4x.
|
7 кл С/р «Линейная функция и её график»
К- №8
1. График функции y(x) – ломаная ACMPK, где
A(-5;6), C(-3;8), M(0;8), P(6;4), K(6;-3).
Построить этот график.
Используя график функции, найти y(x) при
х = 0; 4; -1; 3; 4,5.
При каком значении х значение функции y(x) равно 7; 3; 1; -1?
Указать три значения х, при которых
y(x) > 0, и три значения х, при которых y(x) < 0.
2. Заполнить таблицу, если y(x) = 3,5 - 4x:
x
|
0
|
1
|
-2
|
3
|
|
|
|
|
y(x)
|
|
|
|
|
0,5
|
1,5
|
-2,5
|
0
|
3. Построить график функции y(x) = 4x.
|
7 кл С/р «Линейная функция и её график»
К- №9
1. График функции y(x) – ломаная CDFEK, где
C(-3;-2), D(1;-2), F(3;2), E(6;2), K(0;8).
Построить этот график.
Используя график функции, найти y(x) при
х = 0; -1; 2; 4.
При каком значении х значение функции y(x) равно -1; 3; 6?
Указать три значения х, при которых
y(x) > 0, и три значения х, при которых y(x) < 0.
2. Заполнить таблицу, если y(x) = 2x:
3. Построить график функции y(x) = 7x +1.
|
7 кл С/р «Линейная функция и её график»
К- №10
1. График функции y(x) – ломаная ABCDMN, где
A(-7;5), B(-3;5), C(0;8), D(4;8), M(4;3),
N(6; -3).
Построить этот график.
Используя график функции, найти y(x) при
х = -5; -1; 3; 4,5.
При каком значении х значение функции y(x) равно 6; 2; 1,5?
Указать три значения х, при которых
y(x) > 0, и три значения х, при которых y(x) < 0.
2. Заполнить таблицу, если y(x) = 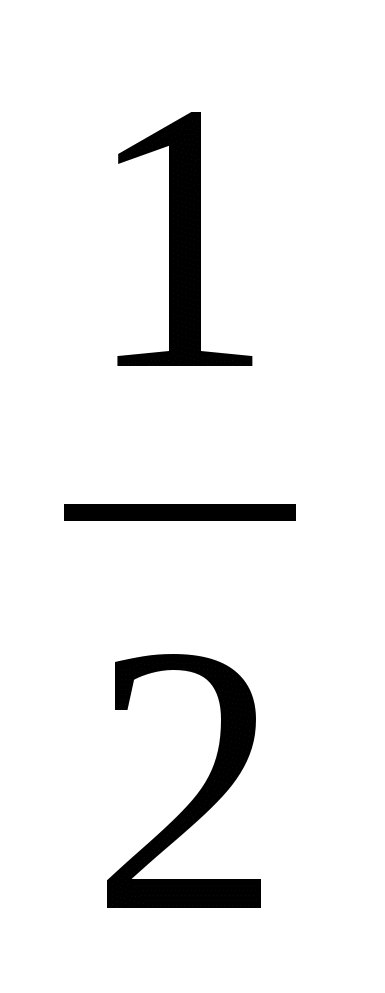 x + 1: x + 1:
x
|
0
|
0,5
|
4
|
-4
|
|
|
|
|
y(x)
|
|
|
|
|
1
|
2
|
-1
|
0,5
|
3. Построить график функции y(x) = 5x - 1.
|
7 кл С/р «Линейная функция и её график»
К- №11
1. График функции y(x) – ломаная ABCDMN, где
A(-10;5), B(-7;5), C(-3;3), D(-1;6), M(3;6), N(6;-3).
Построить этот график.
Используя график функции, найти y(x) при
х = -8; -5; 0; 4.
При каком значении х значение функции y(x) равно 4; 0; -2?
Указать три значения х, при которых
y(x) > 0, и три значения х, при которых y(x) < 0.
2. Заполнить таблицу, если
y(x) = | |
|
|
 Скачать 0.61 Mb.
Скачать 0.61 Mb.