«Пропорция. Масштаб», математика, 6 класс
 Скачать 0.61 Mb. Скачать 0.61 Mb.
|
Слайд №3Какая фигура называется треугольником? Назвать его элементы. Что такое периметр треугольника? Слайд №4Какие отрезки называются медианой, биссектрисой и высотой треугольника? Слайд №5Какой треугольник называется равнобедренным? Равносторонним? Как называются их стороны? Слайд №6Какими свойствами обладает равнобедренный треугольник? 4. УСТНАЯ РАБОТА НА ПОВТОРЕНИЕ 1 (по слайдам презентации). 1) Слайд №7 По рисунку (слайд) доказать, что АВС – равнобедренный. 2) Слайд №8 По рисунку (слайд) доказать, что АВС – равнобедренный. 5. ПРОВЕРКА УСВОЕНИЯ МАТЕРИАЛА (фронтальный опрос с помощью слайдов презентации). Слайд №9Как читается первый признак равенства треугольников? Слайд №10Как читается второй признак равенства треугольников? Слайд 11Как читается третий признак равенства треугольников? 6. УСТНАЯ РАБОТА НА ПОВТОРЕНИЕ 2 (по слайдам презентации). 1) Слайд №12 По рисунку (слайд) найти пары равных треугольников и указать признак равенства. 2) Слайд №13 По рисунку (слайд) найти пары равных треугольников и указать признак равенства. 3) Слайд №14 По рисунку (слайд) найти пары равных треугольников и указать признак равенства. 7. ЗАДАЧИ НА ПОСТРОЕНИЕ. 1) Слайд №15 Как построить угол, равный данному? Повторить алгоритм построения с помощью презентации. 2) Слайд №16 Как построить биссектрису данного угла? Повторить алгоритм построения с помощью презентации. 3) Слайд №17 Как построить перпендикуляр к прямой, проходящий через заданную точку? Повторить алгоритм построения с помощью презентации. 8. МОМЕНТ РЕЛАКСАЦИИ (упражнения для разгрузки и снятия напряжения с глаз), 3 мин. Слайд №18 (музыкальное сопровождение). Исходное положение: сидя в удобной позе, позвоночник прямой, глаза открыты, взгляд устремлен прямо. Выполнять упражнение совсем легко, без напряжения. 1 упражнение. Взгляд направить влево - вправо, вправо - прямо, вверх - прямо, вниз - прямо, без задержки в отведенном положении. Повторить до 5 раз. 2 упражнение. Взгляд смещать по диагонали: влево - вниз - прямо; вправо - вверх - прямо; вправо - вниз - прямо; влево - вверх - прямо и постепенно увеличивать задержки в отведенном положении. Дыхание произвольное. Повторить до 5 раз. 9. РАБОТА У ДОСКИ И В ТЕТРАДЯХ. 1) Слайд №19Дано: АВ = АС; АСЕ = АВД; АЕ = 15 см, ЕС = 10 см, АС = 7 см. а) Доказать: АСЕ = АВД. б) Найти: стороны АВД. 2) Слайд №20 Дано: АО = ОС, ВАО = ДОС. Доказать: АВ = СД. 3) Слайд №21 Задача №181. Дано: радиус окружности; точки А и В. Построить: окружность с радиусом r, проходящую через точки А и В. Наводящие вопросы:
План построения: (демонстрируется на слайде)
Далее учащимся предлагается самостоятельно построить искомую окружность. 10. ИТОГ УРОКА: теоретический тест (5 мин, приложение 1). Критерии оценок:
Ответы к тесту: В – 1: 1) К и Е; 2) Р; 3) б; 4) а, б, в; 5) б; 6) а; 7) в; 8) в; 9) геометрическая, множества, заданном, некоторой; 10) б; 11) б; 12) б; 13) б; 14) формулировка первого признака равенства треугольников. В – 2: 1) M и N; 2) Д; 3) в; 4) а; 5) б; 6) б; 7) а, б, в; 8) в; 9) отрезок, какой-либо; 10) б; 11) в; 12) в; 13) б; 14) формулировка второго признака равенства треугольников. ДОМАШНЕЕ ЗАДАНИЕ: 1) №183; 2) индивидуальные карточки с дифференцированными заданиями. 3. Урок с элементами исследовательской деятельности учащихся по теме «Применение свойств прямоугольного треугольника к решению задач», геометрия, 7 класс. Тип урока: закрепление изученного материала с элементами исследовательской работы учащихся. ЦЕЛИ:
1. ученик должен знать: - употребляемые термины: катеты, гипотенуза, медиана, биссектриса, высота;
2. ученик должен понимать: - как выглядит прямоугольный треугльник;
3. ученик должен уметь:
- применять изученные свойства к решению задач.
ПЛАН УРОКА:
1) фронтальный теоретический опрос учащихся;
ХОД УРОКА: 3. УСТНАЯ РАБОТА НА ПОВТОРЕНИЕ: 1) фронтальный теоретический опрос учащихся:
2) применение свойств прямоугольных треугольников при решении задач по готовым чертежам: 4. ЧТО ТАКОЕ «СВЯЩЕННЫЙ ЕГИПЕТСКИЙ ТРЕУГОЛЬНИК»? Демонстрация исторического материала (показ и рассказ учащихся). А сейчас – немного из истории математики. Что такое «священный египетский треугольник» нам расскажет Сабина, а кто-нибудь из мальчиков поможет ей (ребята держат верёвку, демонстрируя построение прямоугольного треугольника). Известно, что существует так называемый египетский треугольник со сторонами 3: 4: 5 , который называют "совершенным" или "священным". Землемеры Древнего Египта для построения прямого угла использовали бечевку, разделенную узлами на 12 равных частей. Верёвку соединяли так, чтобы в углах были узлы. Рассказывают, что и сейчас при закладывании фундаментов новых домов очень часто строители используют именно этот способ построения прямых углов будущих домов. Историки пишут, что "Египетскому треугольнику" придавали магический смысл. Плутарх писал, что египтяне сравнивали природу Вселенной с треугольником: они символически уподобляли вертикальный катет мужу, основание - жене, а гипотенузу тому, что рождается от них. 5. РЕШЕНИЕ ЗАДАЧ НА ПРИМЕНЕНИЕ СВОЙСТВ ПРЯМОУГОЛЬНОГО ТРЕУГОЛЬНИКА: 1) задача на доказательство свойства медианы прямоугольного треугольника ( с элементами исследовательской работы учащихся на уроке)Ребята, давайте вернёмся к решению устной задачи №5 и проанализируем результат, который мы там получили: АВ = 2СД, СД – высота и медиана, АВ – гипотенуза прямоугольного треугольника. Учащимся предлагается:
ГИПОТЕЗА: если треугольник прямоугольный, то медиана, проведённая из вершины прямого угла, равна половине гипотенузы. Докажем, что наша гипотеза верна. Доказательство: (методом от противного) Пусть ВМ МА и ВМ МС. Пусть ВМ МА, т.к. МА = МС, то ВМ МС. То по теореме о соотношениях между сторонами и углами треугольника против большей стороны лежит больший угол, и наоборот, против меньшей стороны лежит меньший угол. Значит, 4 3 и 1 2. Т.к. по условию 4 + 1 = 90 (по св.1), то 3 + 2 90. Но по условию В = 90. Значит, мы получили противоречие, и наше предположение, что ВМ МА и ВМ МС – неверно. Т.о. наша гипотеза подтвердилась. Утверждение, которое мы сейчас доказали – это ещё одно свойство прямоугольного треугольника: Медиана прямоугольного треугольника, проведённая из вершины прямого угла, равна половине гипотенузы. Давайте сформулируем обратное утверждение: если медиана треугольника равна половине стороны, к которой она проведена, то этот треугольник – прямоугольный. Не всякое обратное утверждение верно. Попробуйте его доказать самостоятельно. Это будет вашим домашним заданием. Что вам надо доказать? Что угол, из которого проведена медиана – прямой (это маленькая подсказка). 2) работа по учебнику: №260. 6. УПРАЖНЕНИЯ ПО ЗДОРОВЬЕСБЕРЕЖЕНИЮ для разгрузки и снятия напряжения с глаз и мышц спины и шеи, 3 мин.
7. ПРИМЕНЕНИЕ СВОЙСТВ ПРЯМОУГОЛЬНЫХ ТРЕУГОЛЬНИКОВ в технике и астрономии. Уголковый отражатель. Доклад учащихся. Мы знаем, что сумма двух острых углов прямоугольного треугольника равна 90. Это свойство лежит в основе конструкции простейшего уголкового отражателя. Как он устроен и где применяется нам расскажет Захарова Юля. 8. ИТОГ УРОКА:
Домашнее задание: 1) доказать признак прямоугольного треугольника; 2) №259. 5. 4. Урок с применением ИКТ и ЦОР с элементами исследовательской деятельности учащихся по теме «Прямоугольная система координат на плоскости. График функции», алгебра, 7 класс. Тип урока: Изучение нового материала. Цели:
ПЛАН УРОКА
ХОД УРОКА I. Организационный момент. Вступительное слово учителя. Сообщение учителем темы и цели урока. II. Работа на повторение. 1. Взаимное расположение двух прямых на плоскости. Рассмотрим чертежи: 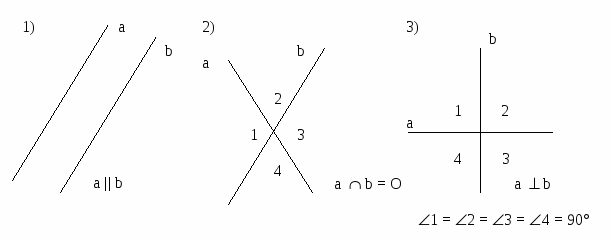 2. Координатная прямая. Координаты точки прямой. 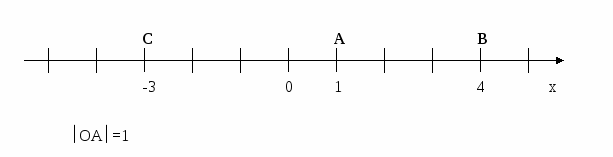 Прямую с выбранными на ней началом отсчёта, единичным отрезком и положительным направлением называют координатной прямой. Число, показывающее положение точки на прямой, называют координатой этой точки. Например, А( 1 ), В( 4 ), С( -3 ). 3. Координатная плоскость. 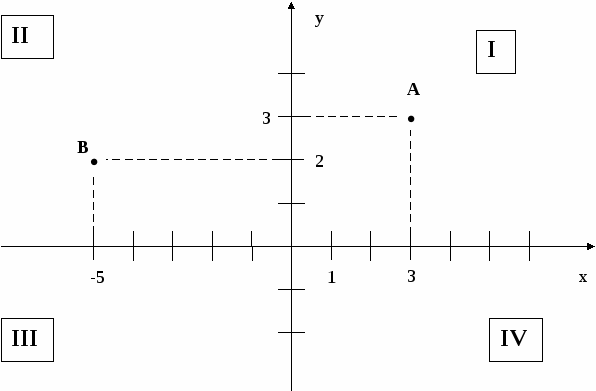 1) Определение координат точки по её расположению на координатной плоскости (устная работа по рисунку). Прямая может располагаться не только горизонтально, но и вертикально. Если взять две такие прямые (горизонтальную и вертикальную), совместить их в начале координат и расположить их перпендикулярно друг к другу, то получится прямоугольная система координат на плоскости. Координатные прямые называются осями координат: ось OX – ось абсцисс ось OY – ось ординат. Прямые углы, образованные осями координат, называются координатными углами или координатными четвертями. Их нумеруют римскими цифрами, начиная с правого верхнего угла против часовой стрелки. Для любого математического понятия мы можем привести пример из окружающей нас действительности. Например,:
А что напоминает нам координатная плоскость? 1) зрительный зал в кинотеатре: ряд и место указаны на билете; 2) 2 пересекающиеся улицы в городе или у нас в селе. Когда почтальон разносит почту, он ориентируется по названию улицы и номеру дома. Значит, для определения положения точки на плоскости одной координаты нам уже недостаточно. Каждой точке А на координатной плоскости соответствует пара чисел: её абсцисса и ордината. А(x;y) или А(3;3) на рисунке. Всегда на первом месте пишут абсциссу точки (х), а на втором – её ординату (y): В(-5;2). Устная работа на закрепление определения координат точек по заданному рисунку.
2. Построение точки по заданным координатам. Работа в парах по обучающей программе. Используется цифровой образовательный ресурс: контрольно-обучающая программа «6_qrafs.zip. About Математика 53 Арифметика. Построение графиков. Демонстрационная версия. Copyriqht Гесслер Дмитрий Михайлович. dmqessler@nm.ru» 1) Выбрать тренажёр – координатная плоскость – уровень 1. Точка имеет координаты (0;0), её можно передвигать при нажатой левой клавише. Отметьте на координатной плоскости точку А(5;-2). 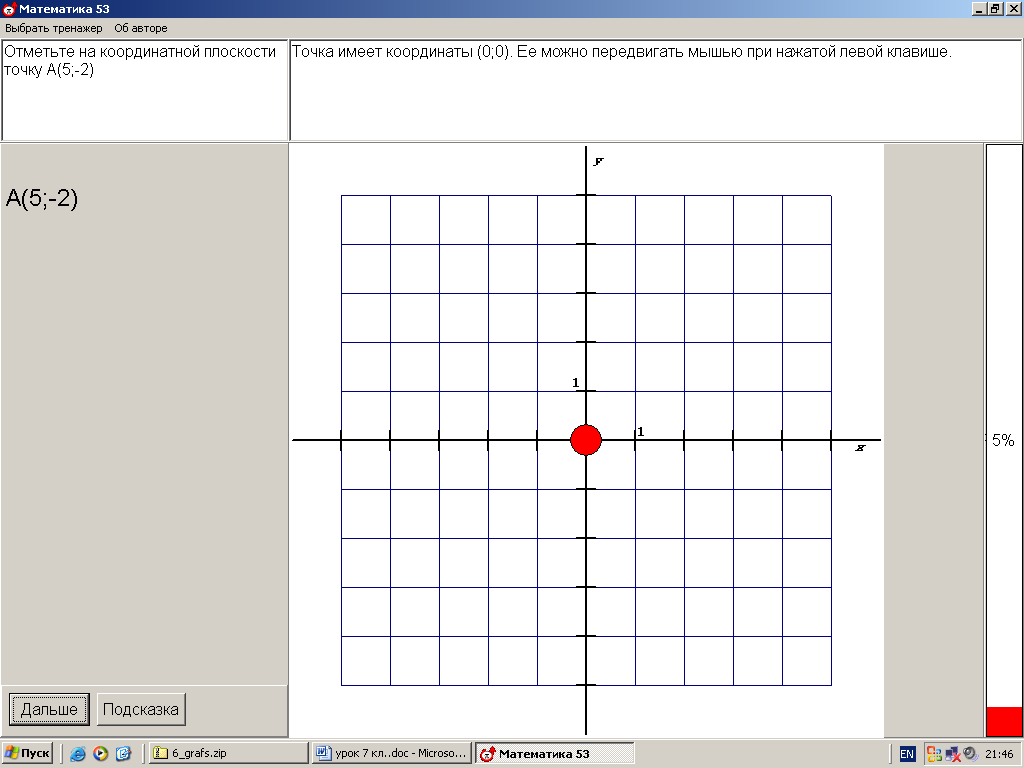 После выполнения задания нажать кнопку «Дальше» - в случае правильного решения появится новая точка с другими координатами. Если же решение было неверным – появится всплывающее окно – подсказка «Ошибка». В правой колонке показана шкала выполнения заданий в %. В случае неверного решения количество % уменьшается. 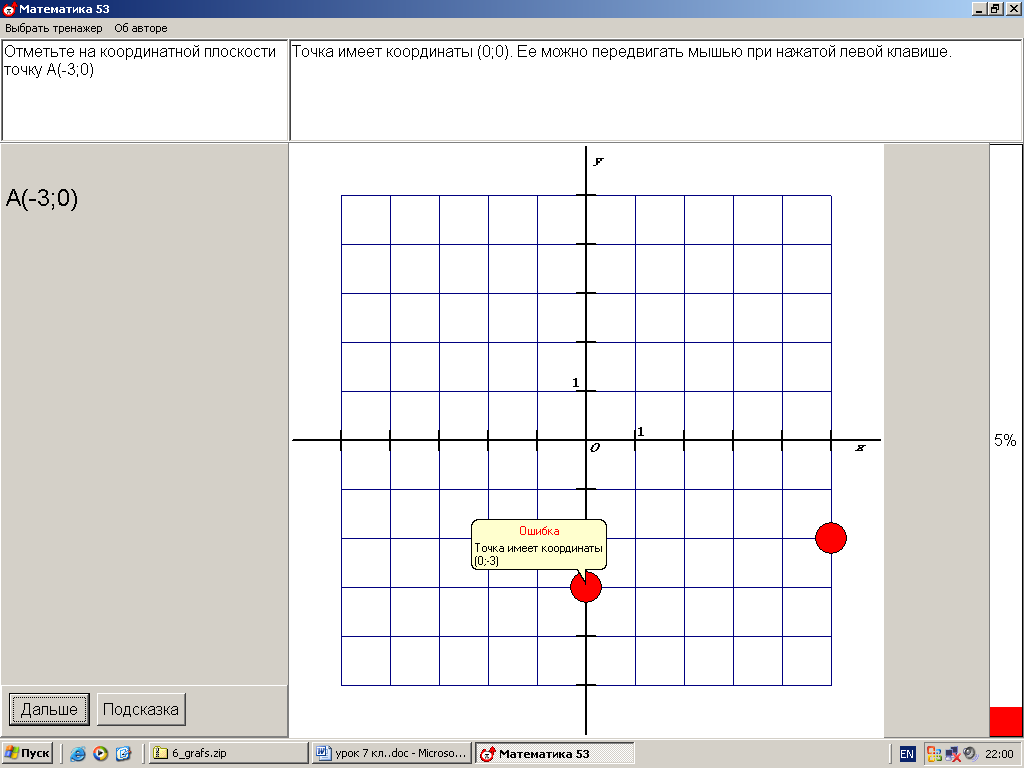 2) Выбрать тренажёр – координатная плоскость – тренажёр 2. Определите координаты выделенной точки. 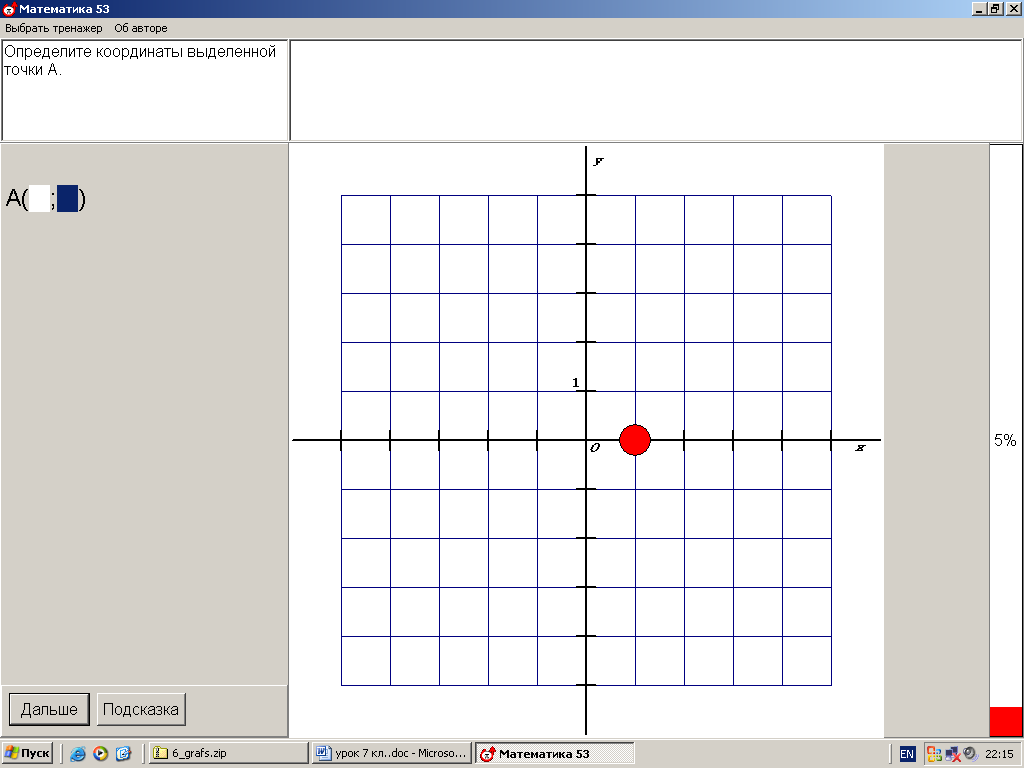 В пустые окна надо впечатать числа, которые являются координатами указанной точки. После выполнения задания нажать кнопку «Дальше» - в случае правильного решения появится новая точка. Если же решение было неверным – появится всплывающее окно – подсказка «Ошибка». Количество % в правой колонке при этом уменьшится. 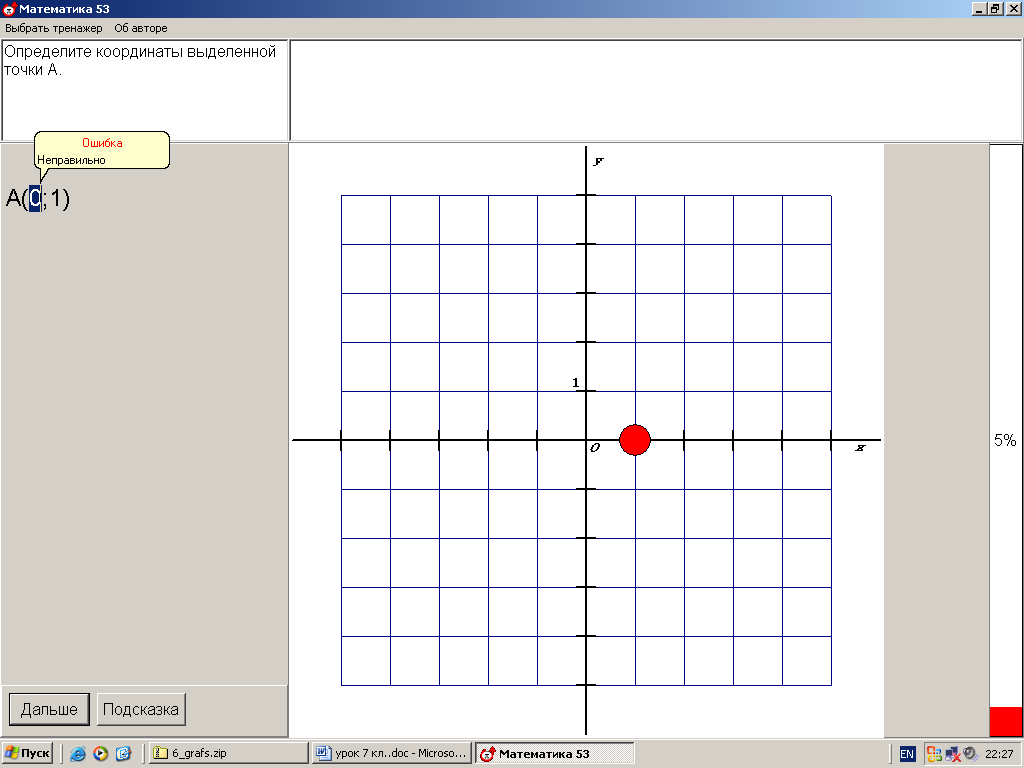 3. Самостоятельная работа обучающего характера – построение фигуры животного или растения по заданным координатам. Используются цифровые образовательные ресурсы: контрольно - обучающая программа «Рисуем по координатам» и электронный практикум по теме «Координатная плоскость». 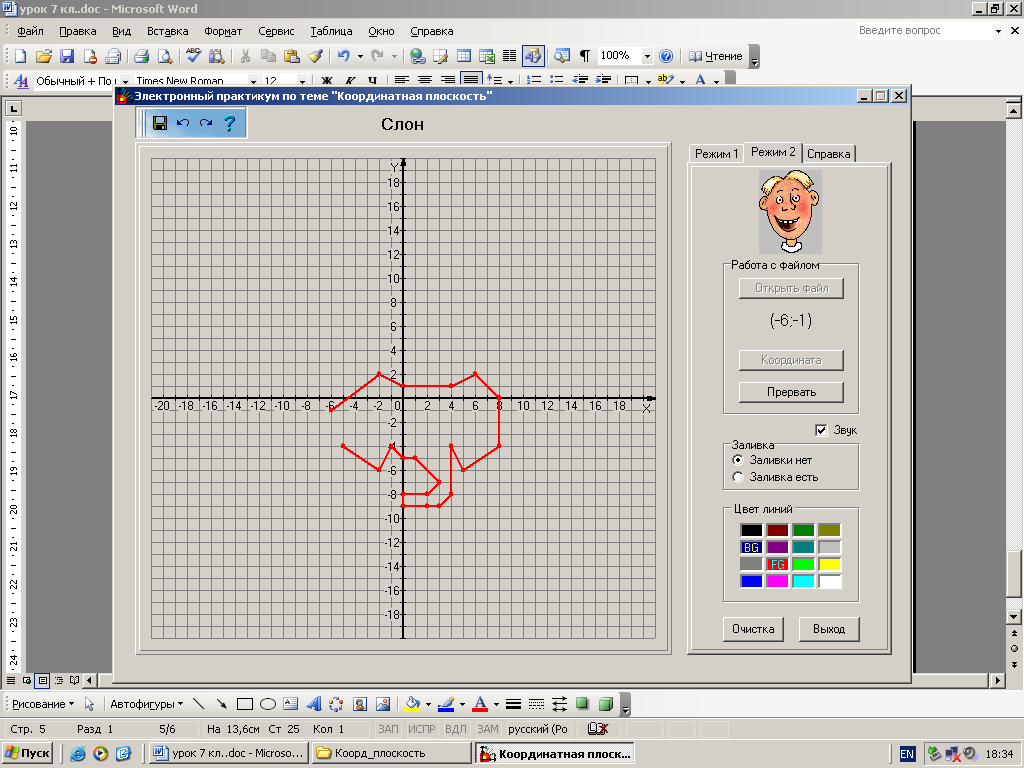 Достройте на рисунке фигурку тюленя, предварительно решив уравнения двух вариантов. Корни уравнений В – 1 являются абсциссами, а корни уравнений В – 2 являются ординатами искомых точек заданной фигурки. 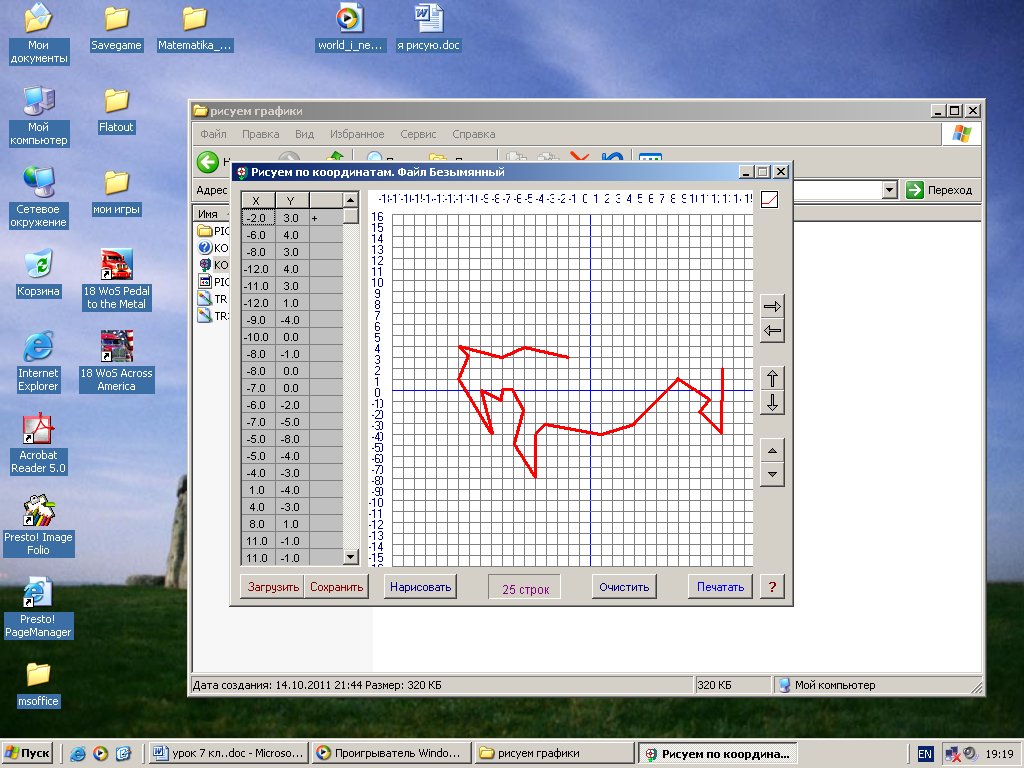 В – 1 В – 2 1) 60 : ( х + 5) = 12 1) ( 7 – y ) 12 = 36 Точка (0;5) 2) 36 – ( 5х – 11 ) = 12 2) 205y – 212 = 403 Точка (7;3) 3) 487 + 17х = 572 3) ( 2y – 5 ) + 38 = 43 Точка (5;5) 4) 2585 : ( 7 + 8х ) = 47 4) 1479 : ( 7y – 5 ) = 29 Точка (6;8) 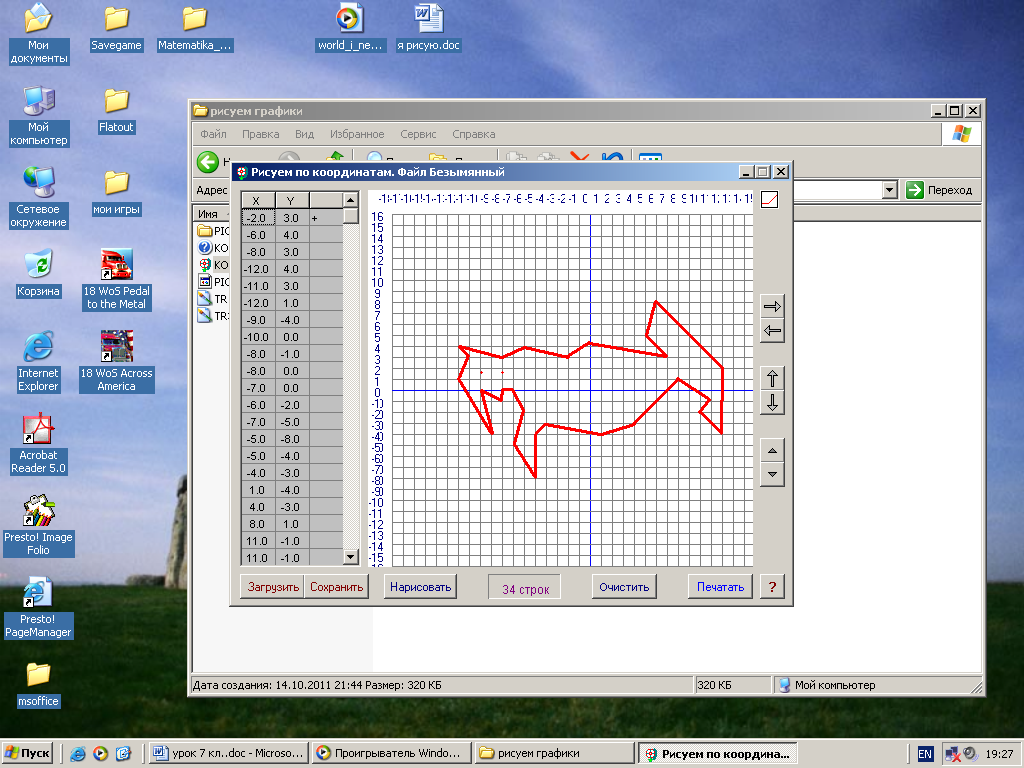 III. Момент релаксации: комплекс упражнений для глаз (3 мин). IV. Изучение новой темы. Фигура, которую мы составили – ломаная. Это линия, которую называют графиком некоторой функции. Опр. Графиком функции y(x) называется множество всех точек плоскости, абсциссы которых равны значениям независимой переменной х, а ординаты – соответствующим значениям зависимой переменной y. Рассмотрим функцию y = x2 – 2x, где -1 ≤ х ≤ 3 – область определения функции. Составим таблицу значений этой функции с шагом 0,5:
Построим пары чисел (х;y) в прямоугольной системе координат, если при составлении таблицы шаг выбрать ещё меньше, то получим ещё больше пар значений (х;y). Все такие точки образуют график функции y = x2 – 2x на промежутке -1 ≤ х ≤ 3. 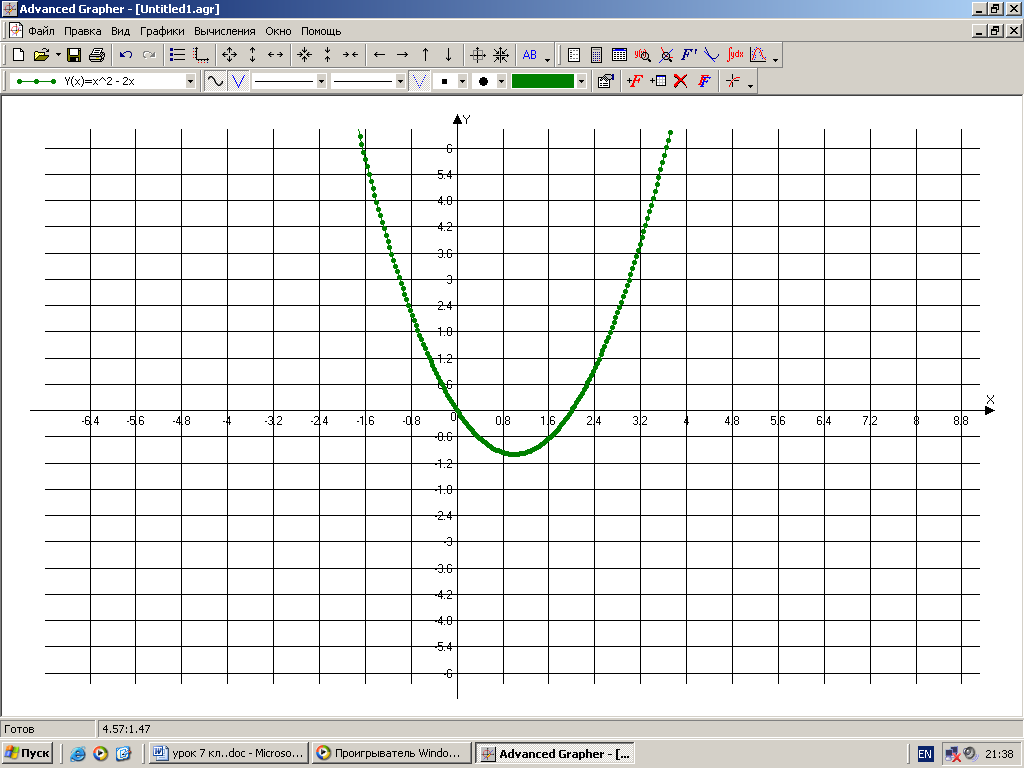 По определению графика функции, все точки (х0; y0), которые удовлетворяют функциональной зависимости, расположены на графике функции. Любые другие точки, координаты которых не удовлетворяют зависимости y(x), не лежат на графике этой функции. Например, принадлежат ли графику данной функции точки А(-2;5) и В(4;8)? а) Найдём значение функции при х = -2: y(-2) = (-2)2 – 2 (-2) = 4 + 4 = 8, т.к. 8 5, то А(-2;5) не принадлежит графику функции. б) Найдём значение функции при х = 4: y(4) = 42 – 2 4 = 16 - 8 = 8, значит, В(4;8) принадлежит графику функции. V. Работа по учебнику на закрепление. №283 – заполнить таблицу. VI. Итог урока. Домашнее задание творческого характера. Капитан Флинт, как вы знаете, спрятал свои сокровища на острове. Перед смертью старый пират решил оставить для потомков шифрованное письмо – описание пути, ведущего к кладу, и место, где он спрятан. Капитан взял карту острова, нарисовал на ней оси координат, выбрал единицы. В качестве главных ориентиров он указал координаты 4-х дубов (3;5), (-2;7), (_3;4) и (3;-1). Клад находился в точке пересечения отрезков, соединяющих первый и третий, второй и четвёртый дубы. Постройте точки, соответствующие местоположению дубов, и определите координаты пещеры с сокровищами. А затем заполните карту острова: нанесите на неё различные объекты –
5. Урок с применением ИКТ и ЦОР с элементами исследовательской деятельности учащихся по теме «Линейная функция и её график», алгебра, 7 класс.(2ч.) Тип урока: Изучение нового материала. Цели:
y = kx + b.
ПЛАН УРОКА
1. Работа по тренажёру «Координатная плоскость». 2. Работа по обучающей программе «Математика 53».
1. Теория. 2. Практика.
1. Работа по обучающей программе «Математика 53». 2. Работа по электронному учебному изданию «Математика 5-11. Новые возможности» (изд-во «Дрофа»). 3. Работа по учебнику.
ХОД УРОКА I. Организационный момент. Вступительное слово учителя. Сообщение учителем темы и цели урока. II. Проверка домашнего задания. Устная работа на повторение с применением ЦОР. 1. Работа по тренажёру «Координатная плоскость» (автор Хайманова Т.Я.): Задание: укажите координаты выделенной точки. Клавиша «Начало» (появляется точка) – ввести значения для х и y – клавиша «Принять ответ» – верно (неверно) – клавиша «Ещё точка» - продолжить работу. 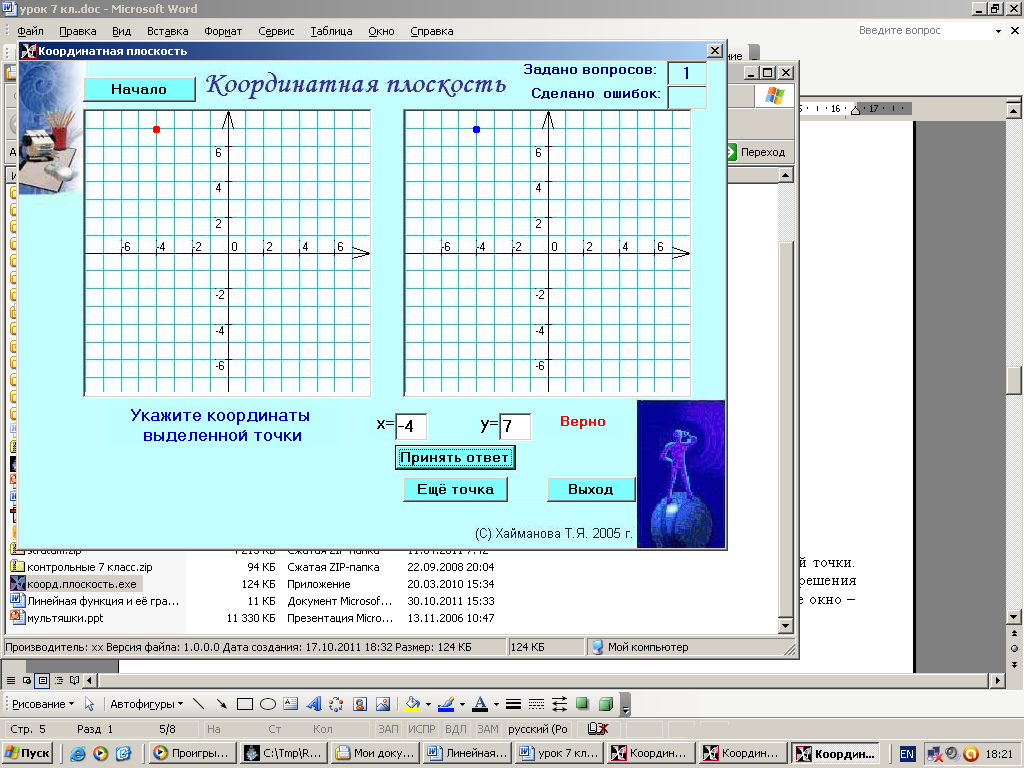 2. Используется цифровой образовательный ресурс: контрольно-обучающая программа «6_qrafs.zip. About Математика 53 Арифметика. Построение графиков. Демонстрационная версия. Copyriqht Гесслер Дмитрий Михайлович. dmqessler@nm.ru» Выбрать тренажёр – координатная плоскость – тренажёр 2. Задание: определите координаты выделенной точки: 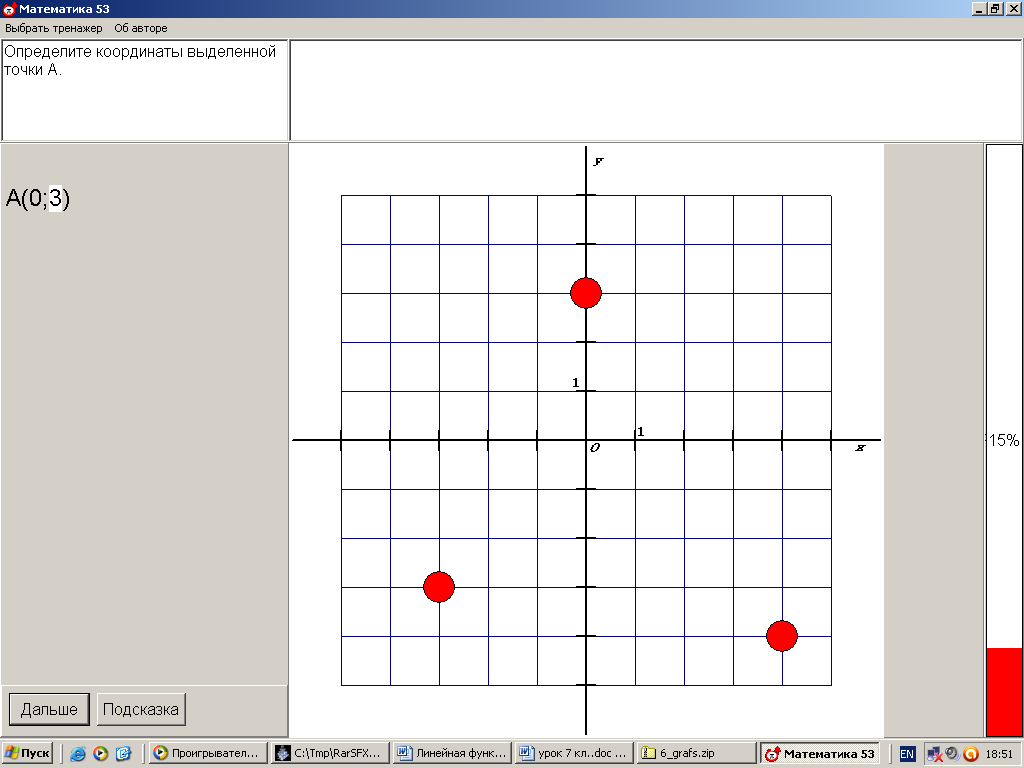 В пустые окна надо впечатать числа, которые являются координатами указанной точки. После выполнения задания нажать кнопку «Дальше» - в случае правильного решения появится новая точка. Если же решение было неверным – появится всплывающее окно – подсказка «Ошибка». Количество % в правой колонке при этом уменьшится. III. Изучение новой темы с применением ЦОР. 1. ТЕОРИЯ Линейной функцией называется функция, которую можно задать формулой вида y = kx + b, где х – независимая переменная, k и b – некоторые числа. Обратить внимание учащихся на то, что независимая переменная х входит в формулу в степени не выше первой. Например, функции: 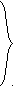 y = 5x – 3 y = -2x + 3 ЛИНЕЙНЫЕ y = 7x + 0, b = 0 ФУНКЦИИ y = -x + 0, b = 0 Прямая пропорциональность y = kx является частным случаем линейной функции, где b = 0. Графиком линейной функции является прямая линия. Рассмотрим график линейной функции и его построение с помощью обучающей программы (ЦОР № , Единая коллекция образовательных ресурсов). а) Составим таблицу значений для функции y = 1,5x – 4. Вычислим и подставим в таблицу полученные значения функции. В случае правильного вычисления число окрашивается в зелёный цвет, а в системе координат при этом появляется точка, затем при полном заполнении таблицы появляется прямая линия – график функции y = 1,5x – 4. 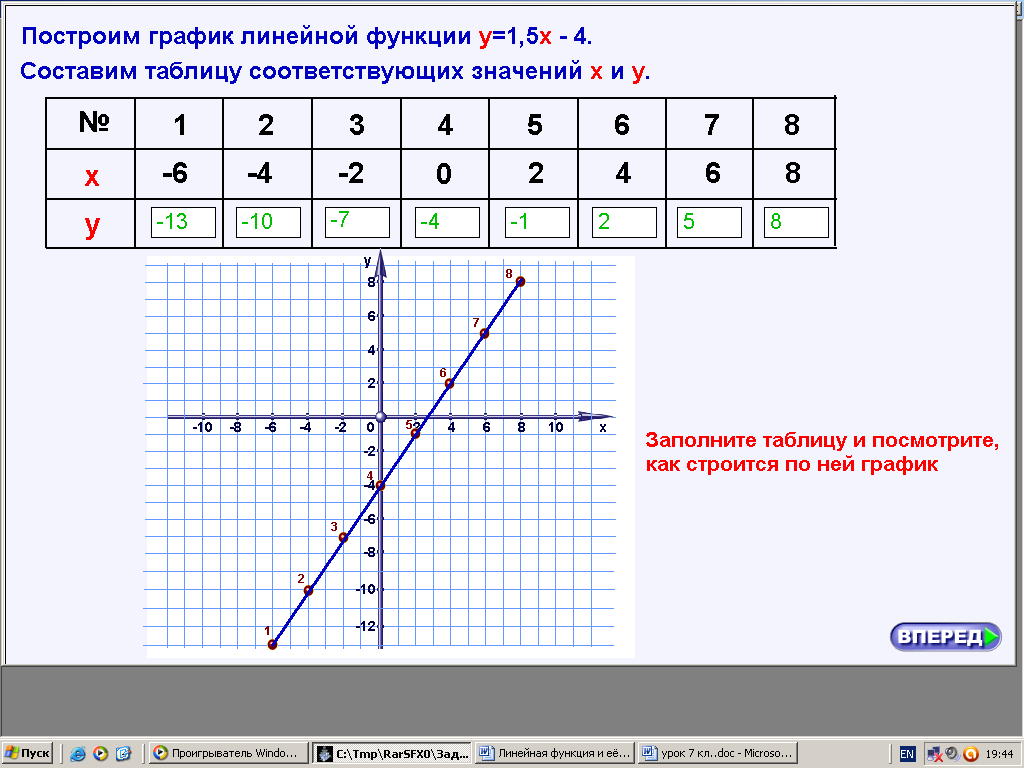 Т.к. для построения прямой на плоскости достаточно знать координаты двух точек, через которые она проходит, то для построения графика линейной функции достаточно найти эти точки. 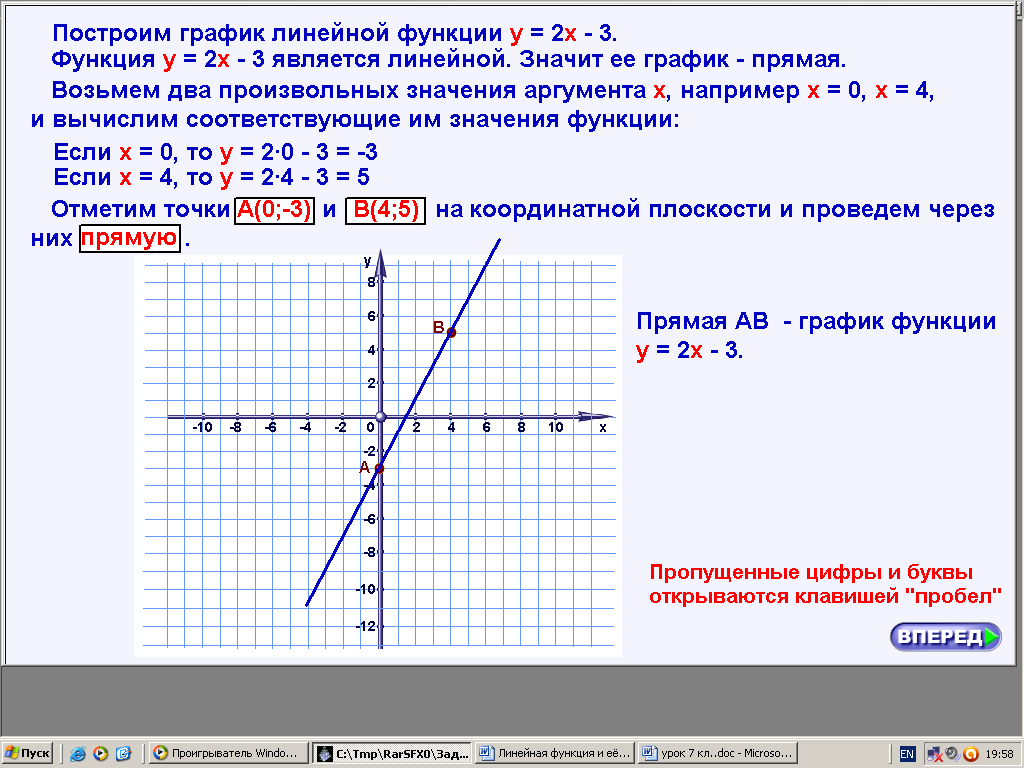 б) Рассмотрим расположение графика функции y = kx + b в зависимости от значений k и b 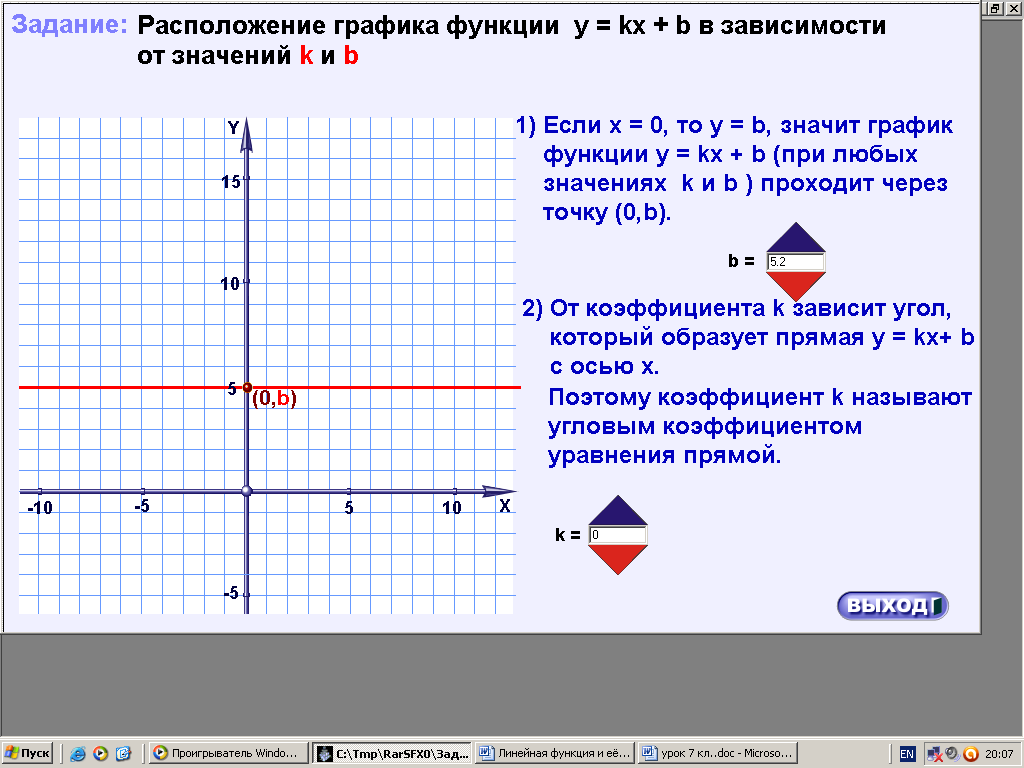 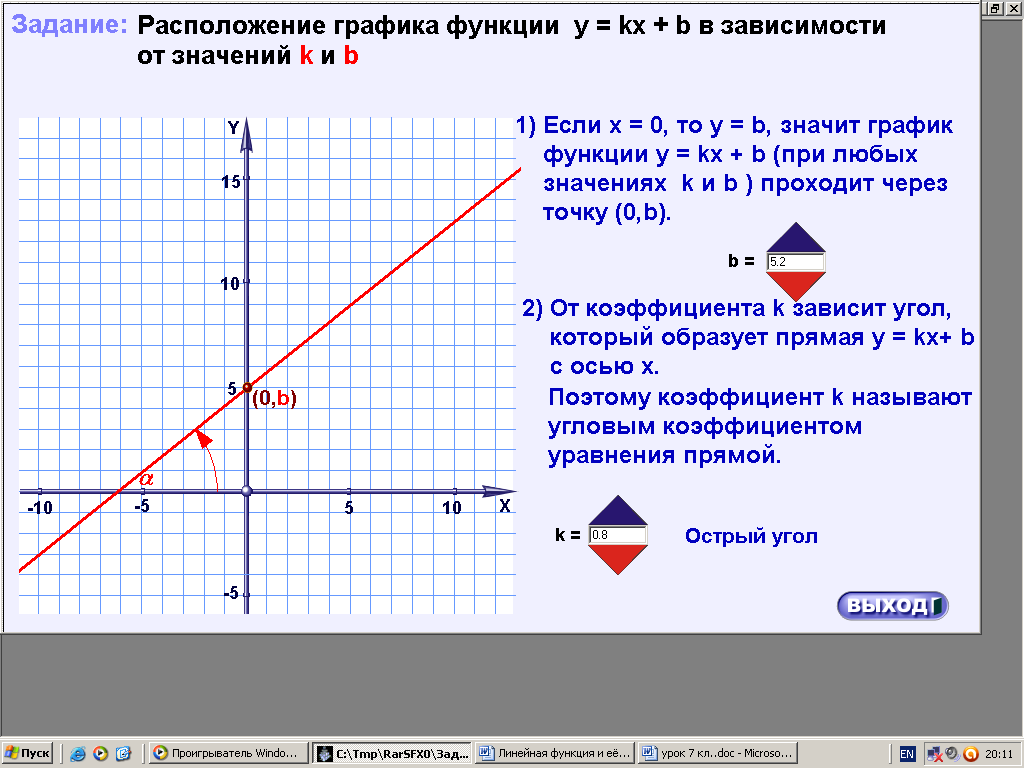 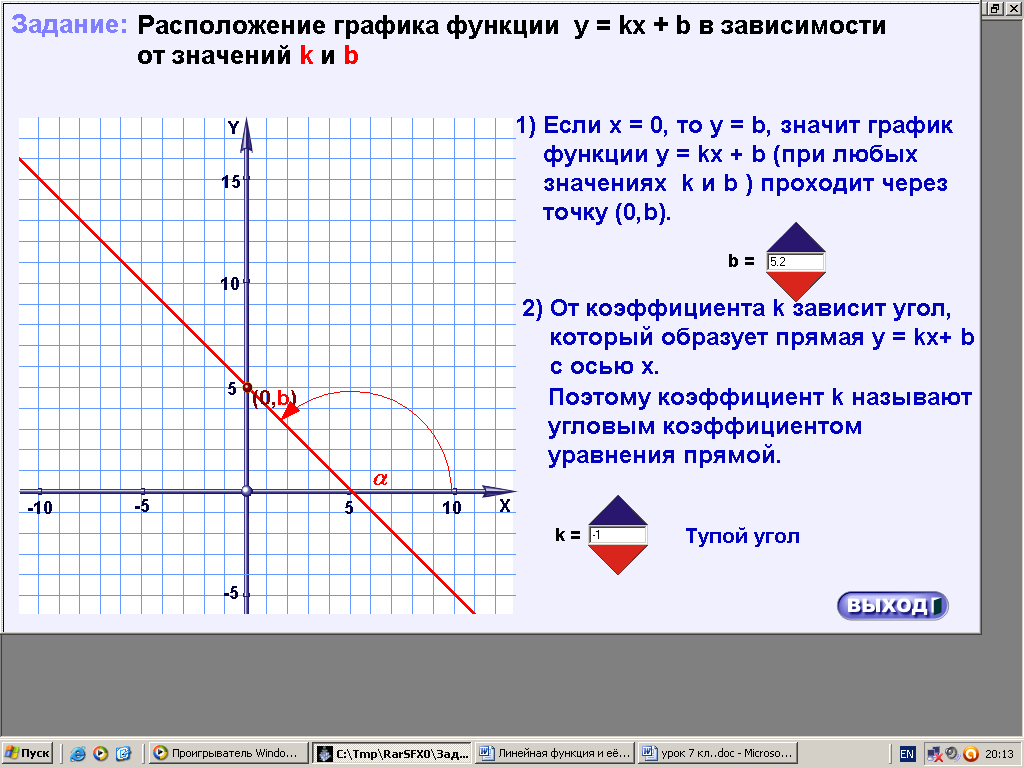 2. ПРАКТИКА 1. Задание: определить коэффициенты k и b по заданным графикам a,b,c и d. 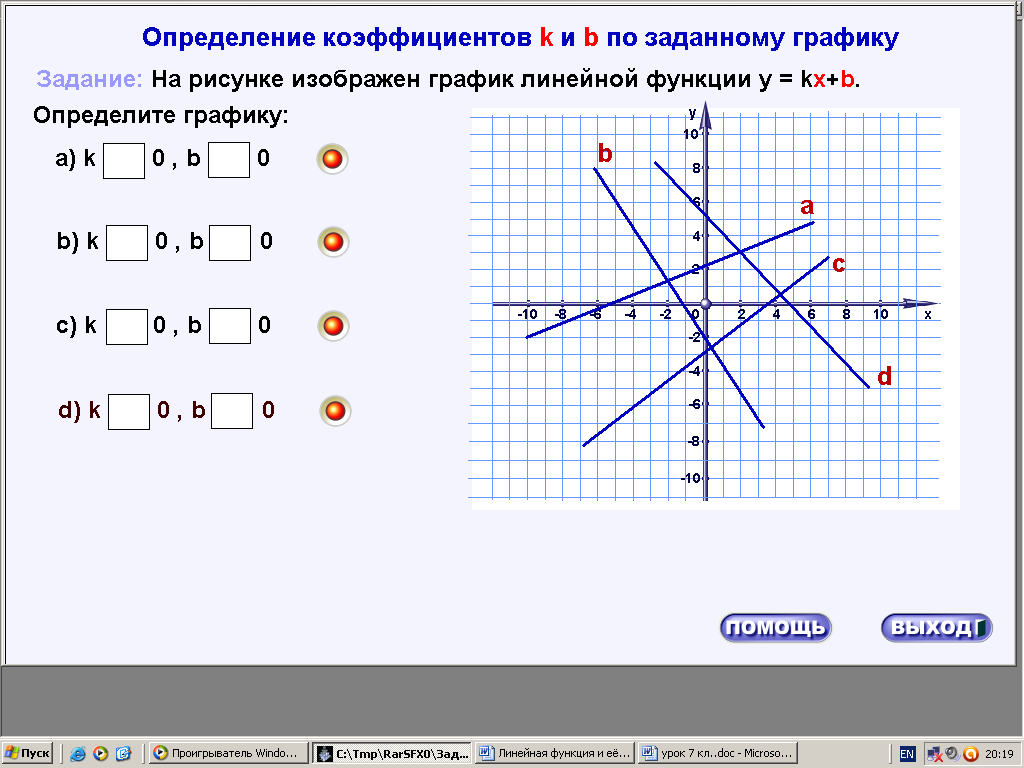 а) k > 0, b = 2 > 0; б) k < 0, b = -2 < 0; в) k > 0, b = -3 < 0; г) k < 0, b = 5 > 0. 2. Задание: построение прямой y = kx + b, проходящей через две точки. Отмечаем точки на координатной плоскости (переносом), подбираем значения k и b, проводим прямую через указанные точки. 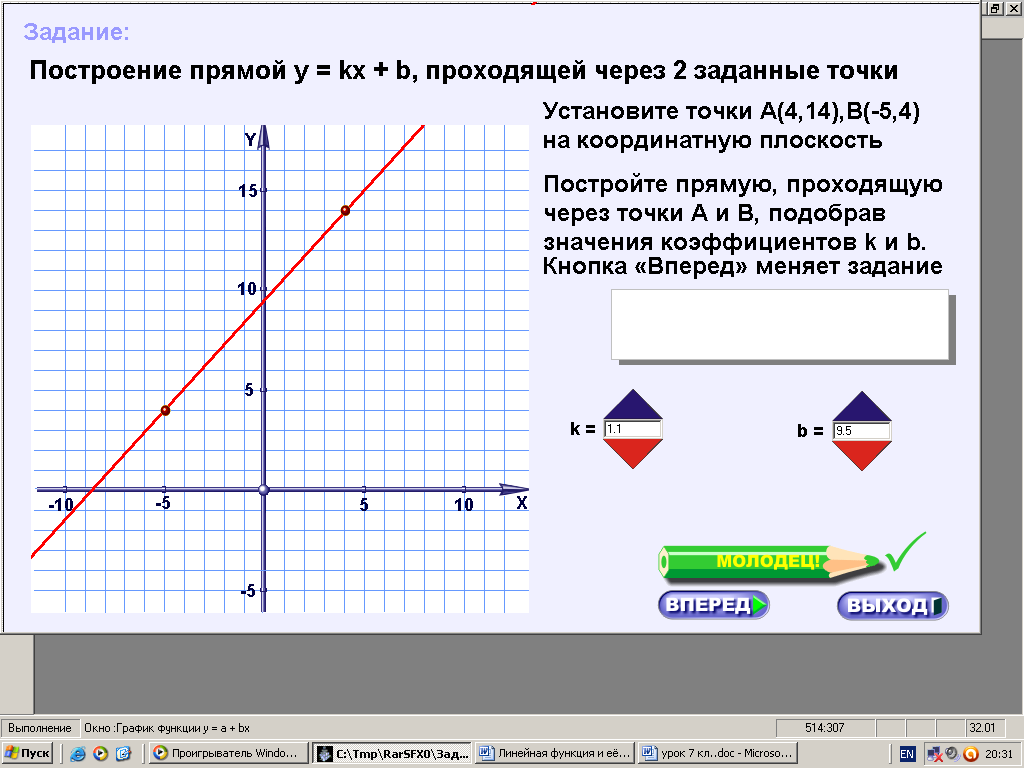 3. Задание: определить коэффициенты k и b по заданному графику линейной функции (при нажатии на клавишу «Вперёд» меняется график функции): 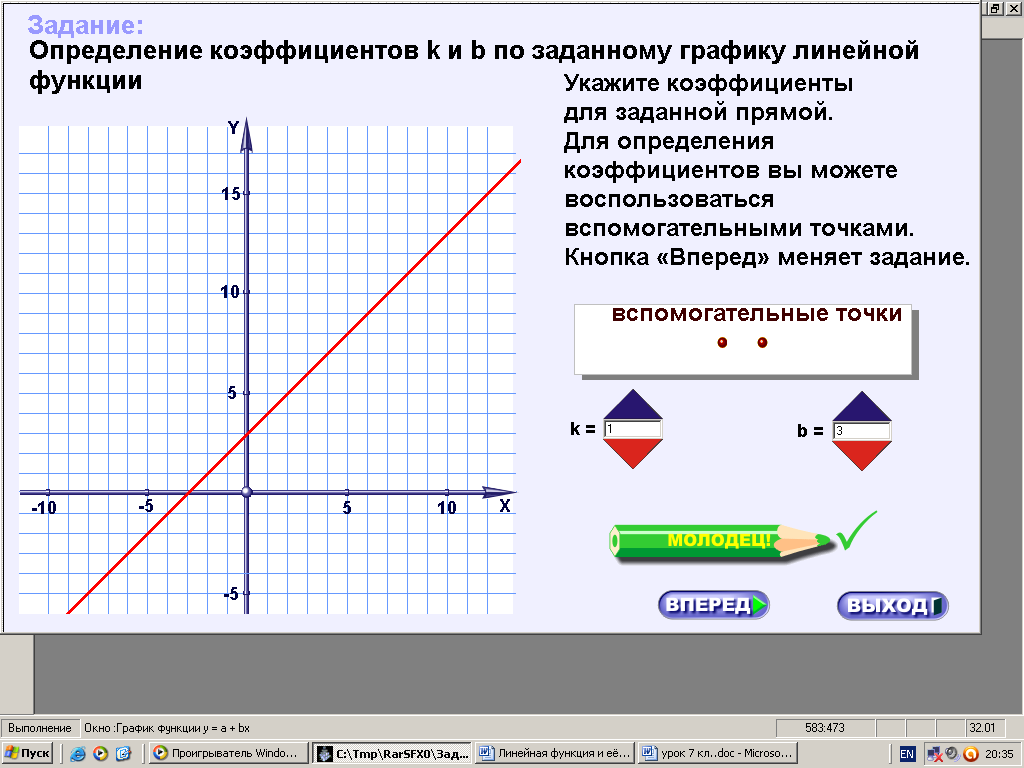 1) b = 3, (-3;0), y = 0, 0 = k (-3) + 3 -3k + 3 = 0 -3k = -3 k = -3 : (-3) k = 1 2) k = 0, b = 7. IV. Решение упражнений на закрепление изученного материала. 1. Используется цифровой образовательный ресурс: контрольно-обучающая программа «6_qrafs.zip. About Математика 53 Арифметика. Построение графиков. Демонстрационная версия. Copyriqht Гесслер Дмитрий Михайлович. dmqessler@nm.ru» 1) Выбрать тренажёр – линейная функция – уровень 1. Задание: построить график по двум точкам. Значения для х выбираются учащимися произвольно, значения для y вычисляются по заданной формуле, на доске и в тетрадях делаются соответствующие записи. 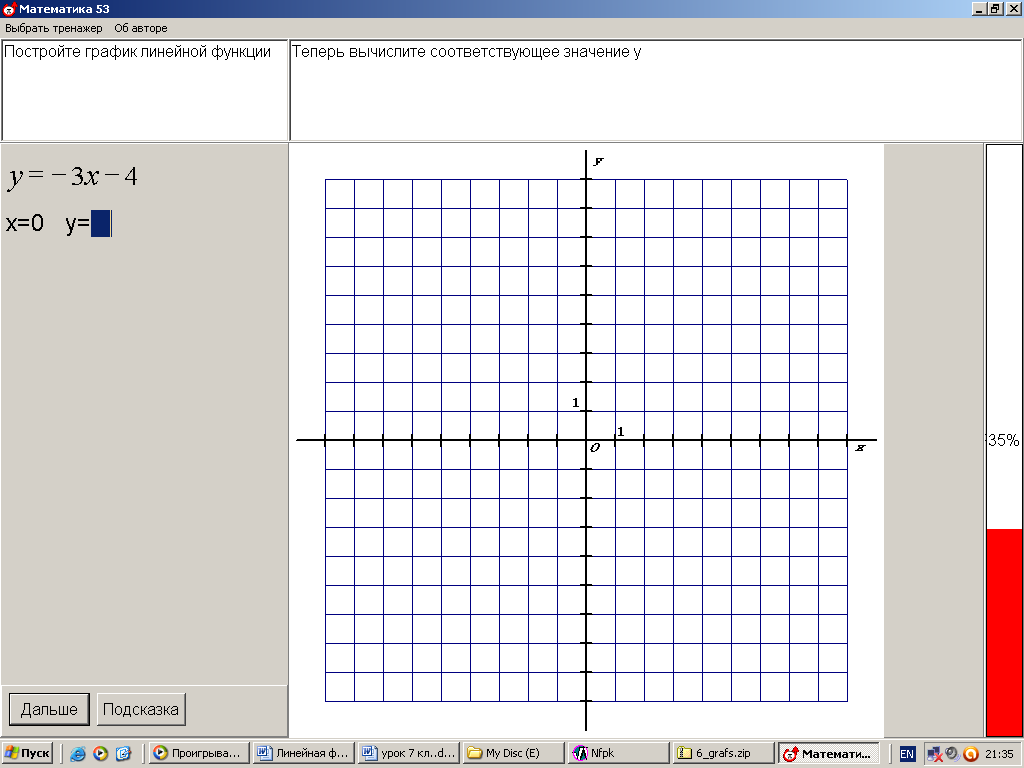 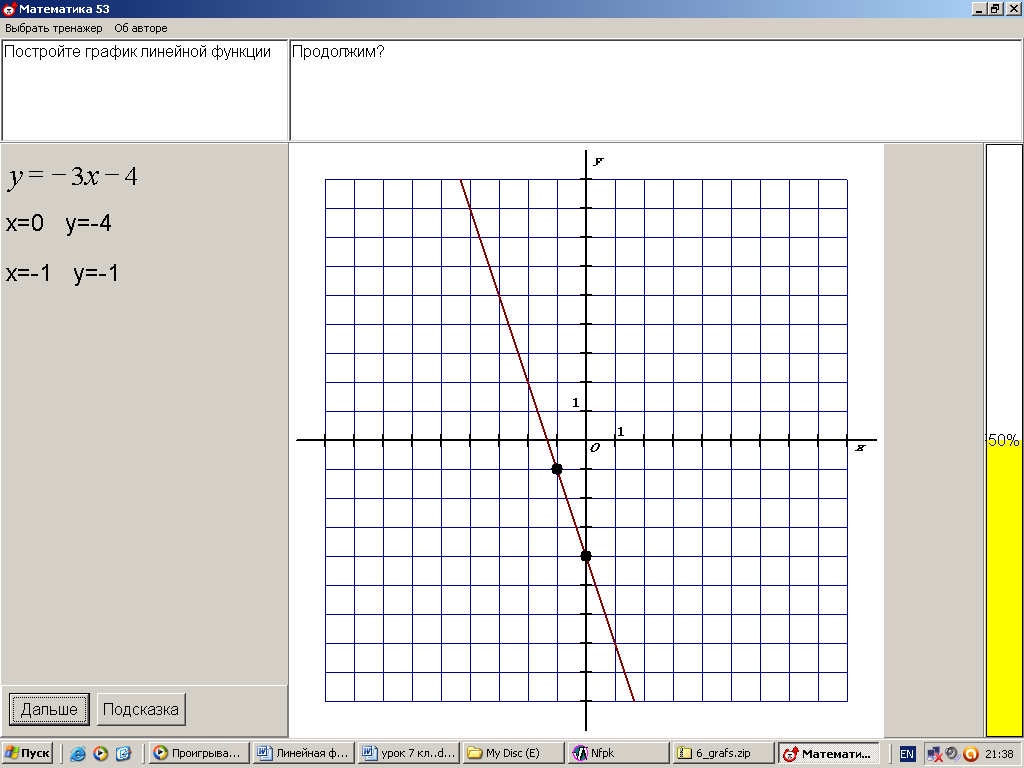 2) Выбрать тренажёр – линейная функция – уровень 2. Задание: переместить прямую на нужное место. 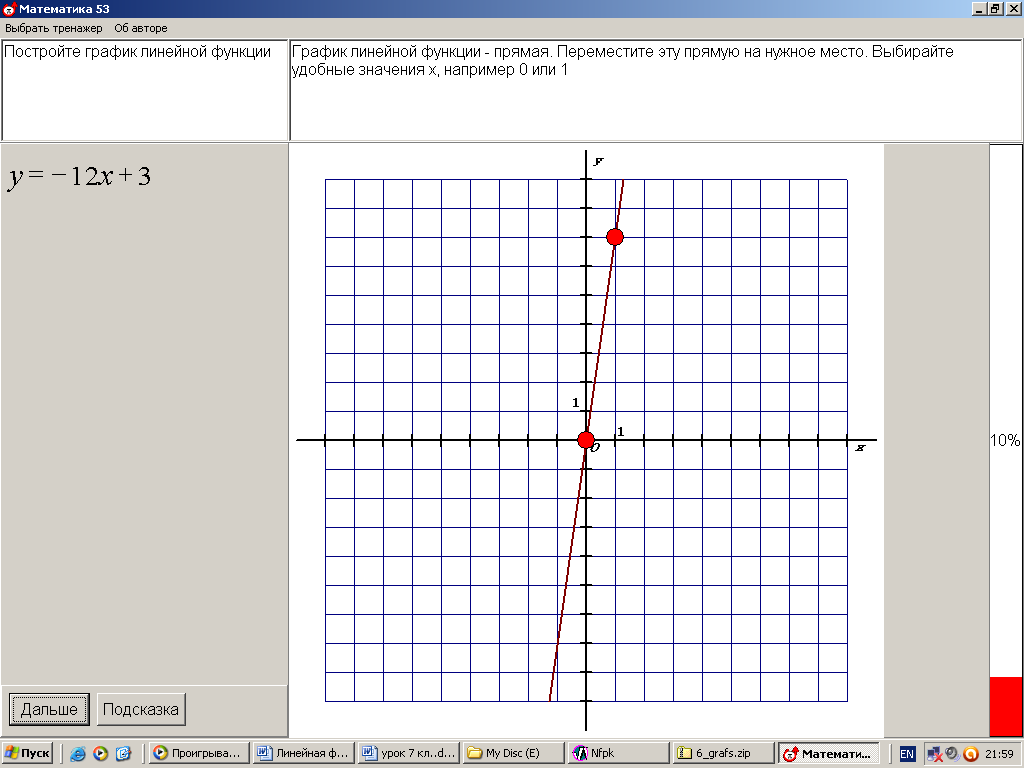 (0; 0) – (0; 3), y(0) = -12 0 + 3 = 3; (1; 7) – (1; -9), y(1) = -12 1 + 3 = -9. 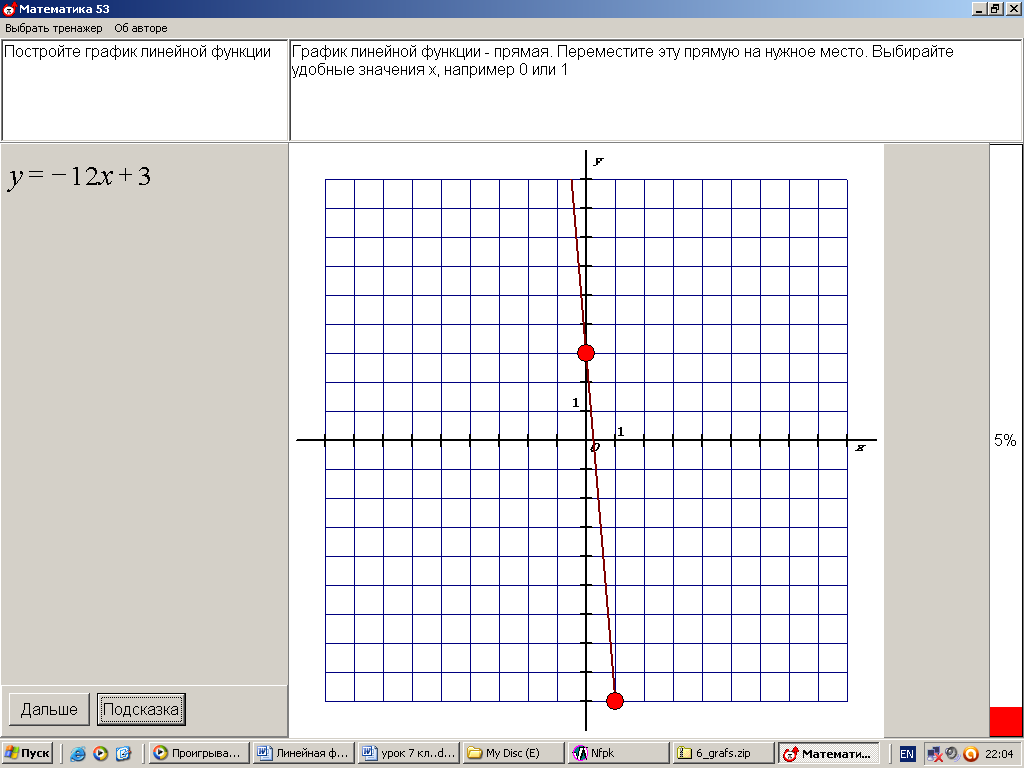 2. Работа по электронному учебному изданию «Математика 5-11. Новые возможности» (изд-во «Дрофа»). Меню: алгебра 7-9 – линейная функция – упражнения. №1. Постройте в одной и той же системе координат графики функций (используйте разные цвета). Необходимые вычисления учащиеся выполняют в тетрадях и у доски: 1) y = 2x +3 2) y = -2x +3 x = 0, y(0) = 3, (0;0); x = 0, y(0) = 3, (0;0); x = 1, y(1) = 2 1 + 3 = 5, (1;5). x = 1, y(1) = -2 1 + 3 = 1, (1;1). 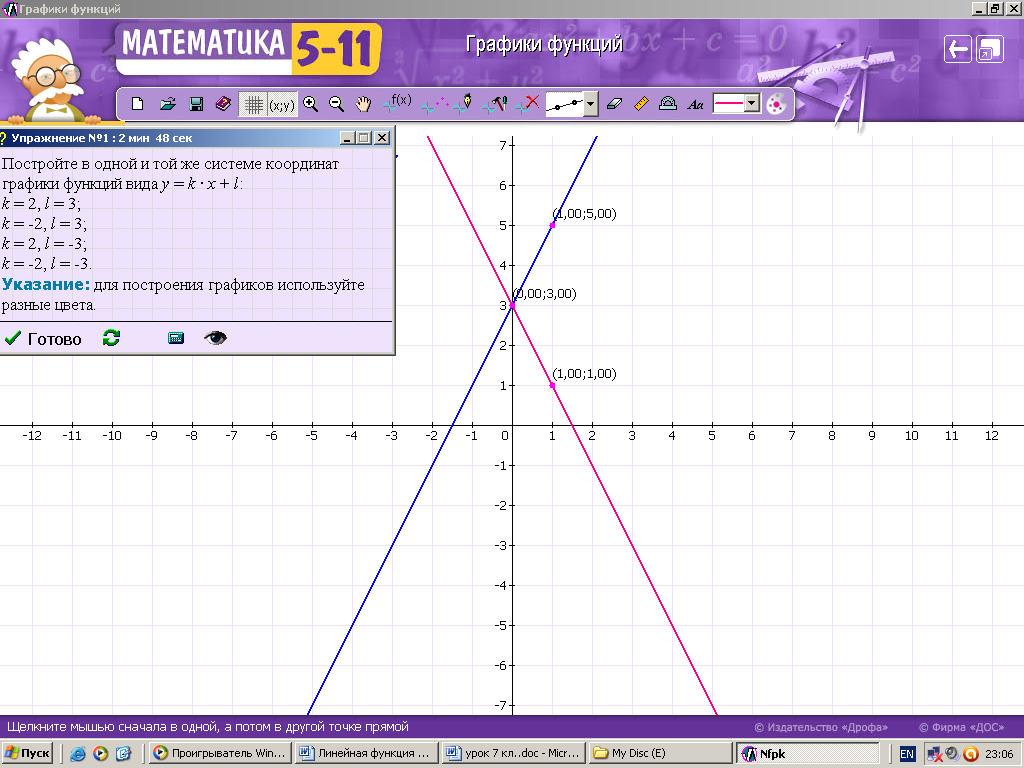 №2. Постройте график функции на заданном интервале. Необходимые вычисления учащиеся выполняют в тетрадях и у доски: y = 3x -1, -3 ≤ x ≤ 3. 1) x = -3, y(-3) = 3 (-3) – 1 = -10, (-3; -10); 2) x = 3, y(3) = 3 3 – 1 = 8, (3; 8). 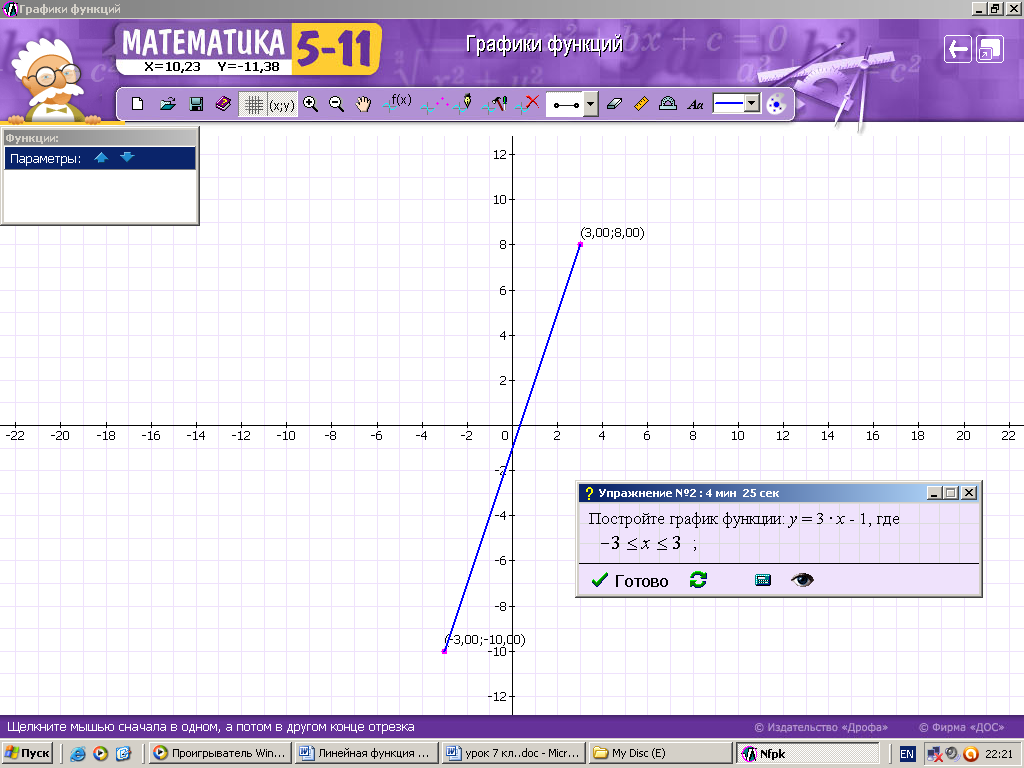 3. Работа по учебнику. Выполнить письменно в тетрадях. №317, №319 (а, в, д). IV. Задача – исследование ( электронное учебное издание «Математика 5-11. Новые возможности», изд-во «Дрофа»). №6 Задание: задайте формулой вида y = kx + b какую-нибудь линейную функцию, обладающую указанными свойствами, и постройте её график. 1) y = 0 при x = 3. 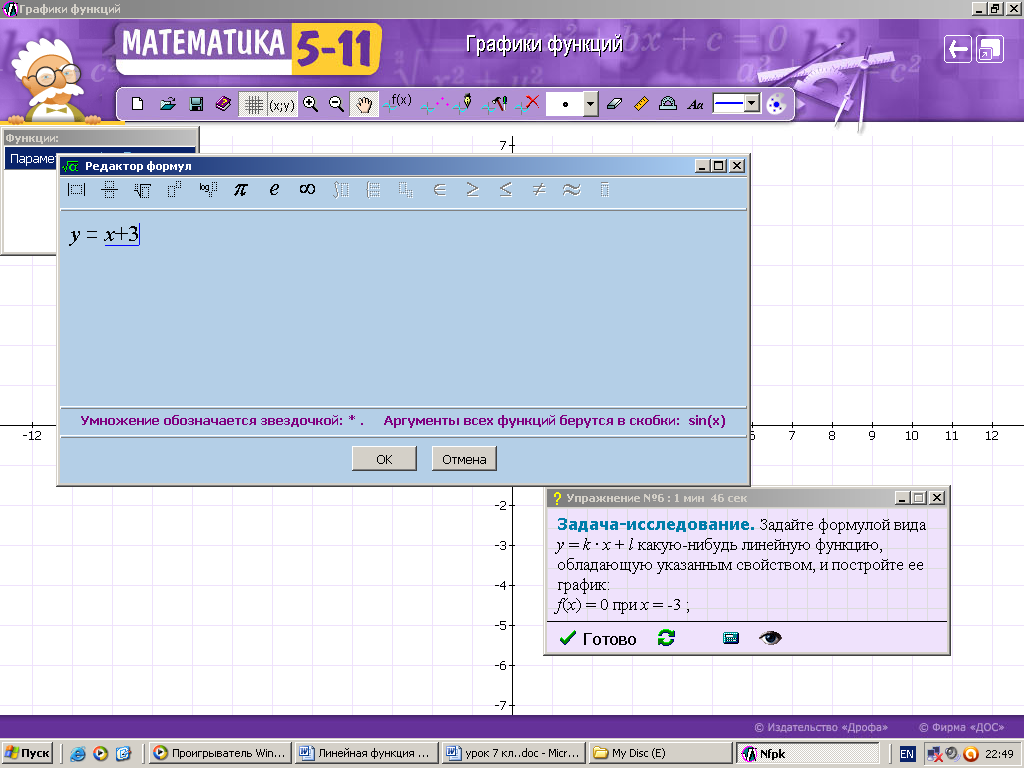 С помощью графических возможностей программы строится график функции y = x + 3: 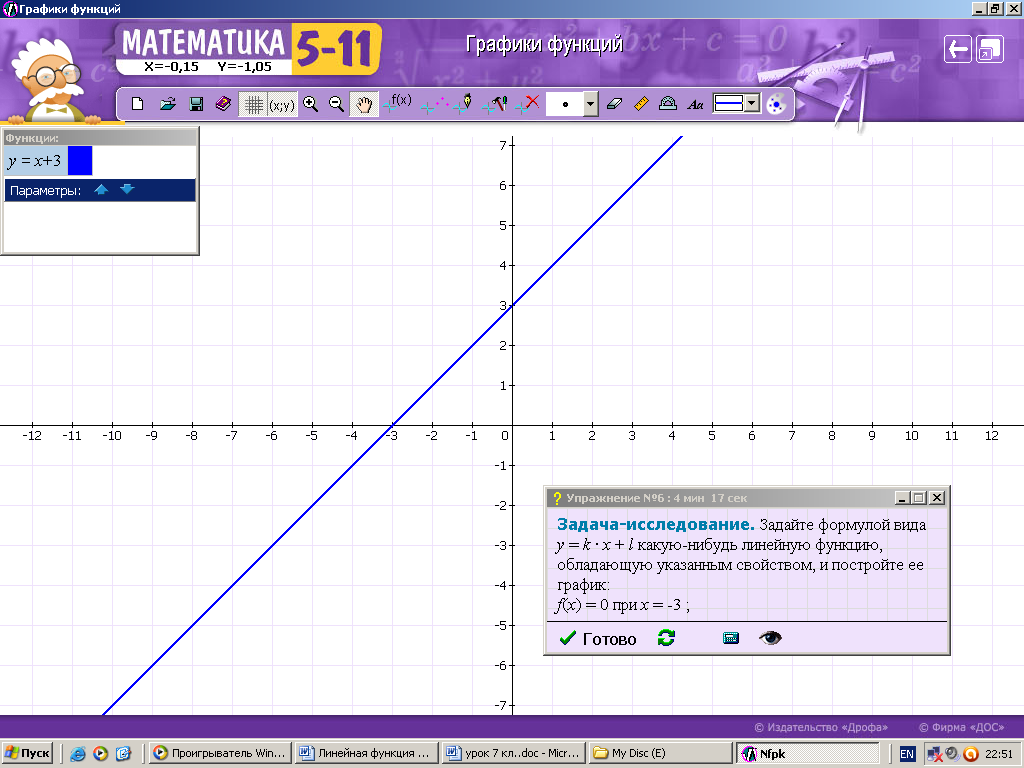 2) y = -3 при х = 0. 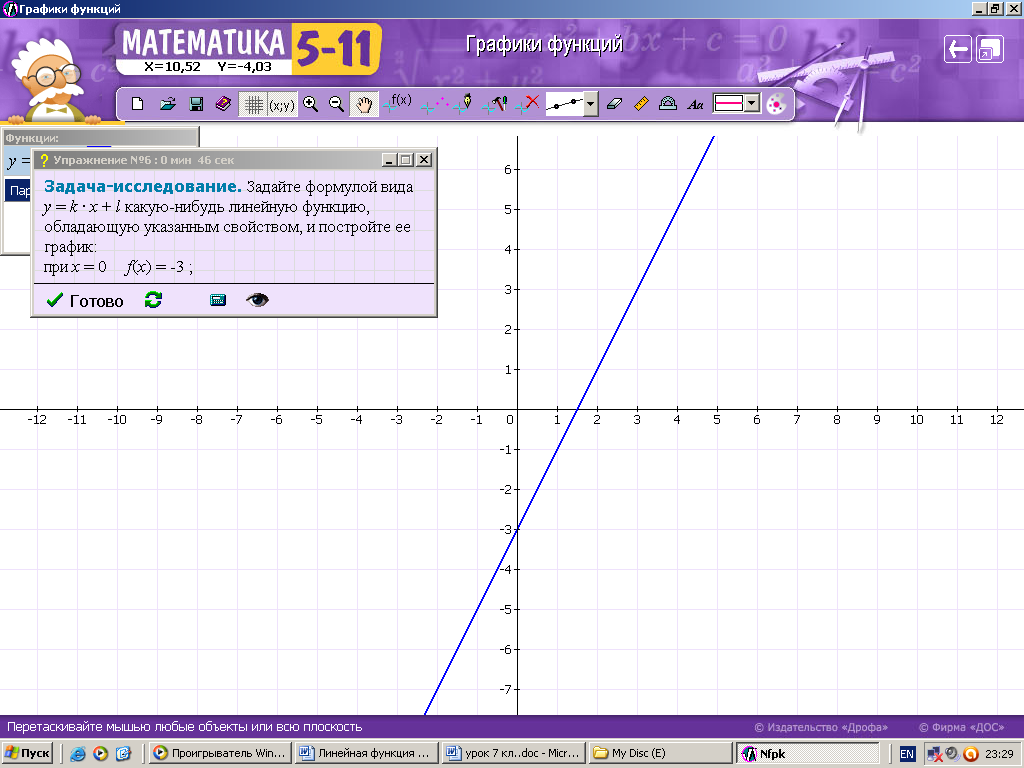 V. Итоги урока. Домашнее задание. Выполнить по учебнику № 318, № 319 (б, г, е). 6. Проверочный тест по теме «Треугольник», геометрия, 7 класс. Ф.И._____________________ Проверочный тест (5-7 мин) |