Решение задач по термодинамике требует знание первого закона термодинамики и уравнения состояния идеального газа (в том случае, если газ можно считать идеальным в условии данной задачи)

Название	Решение задач по термодинамике требует знание первого закона термодинамики и уравнения состояния идеального газа (в том случае, если газ можно считать идеальным в условии данной задачи)
Дата	05.04.2016
Размер	193.78 Kb.
Тип	Решение

1. /Физика/Задания по механике.docx
2. /Физика/Задания по термодинамике.docx

2 имеет у поверхности Земли скорость 600м∕с. Чему равно отношение масс m
Решение задач по термодинамике требует знание первого закона термодинамики и уравнения состояния идеального газа (в том случае, если газ можно считать идеальным в условии данной задачи)

Решение задач по термодинамике требует знание первого закона термодинамики и уравнения состояния идеального газа (в том случае, если газ можно считать идеальным в условии данной задачи).

Первый закон термодинамики отражает закон сохранения энергии и говорит о том, что количество теплоты (энергия) переданное газу, идет на совершение работы газом и увеличение его внутренней энергии.
Q=ΔU+A^’
Так как работа газом совершается только в результате процесса, она является функцией процесса. При этом не в каждом процессе газ может совершать работу. Если процесс идет без изменения объема газа, тогда все переданное газу тепло (энергия) идет на изменение внутренней энергии газа.

Внутренняя энергия идеального газа складывается из кинетической энергии всех молекул (атомов, или других структурных единиц из которых состоит газ). Потенциальная энергия газа, обусловленная взаимодействием между молекулами, при этом отсутствует, так как по определению идеального газа в нем отсутствует взаимодействие между молекулами. Внутренняя энергия идеального газа зависит от количества молекул и средней кинетической энергии молекулы. Учитывая, что температура есть мера средней кинетической энергии молекулы, можно определить внутреннюю энергию идеального газа по формул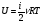е

, где

i- число степеней свободы молекулы:

i=3, если молекула одноатомная;

i=5, если молекула двухатомная;

i=6, если молекула трех и более атомная;

U - внутренняя энергия идеального газа;

ν - количество вещества;

R - универсальная газовая постоянная (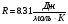

);

T - абсолютная температура газа.

Таким образом, внутренняя энергия газа является функцией состояния, она всегда присутствует и может либо изменяться, либо оставаться неизменной. Судить о том, как изменяется внутренней энергии газа можно по температуре. Если количество вещества остается неизменным, то с увеличением температуры газа увеличивается и его внутренняя энергия, а с уменьшением температуры внутренняя энергия уменьшается. При изотермическом процессе внутренняя энергия газа остается постоянной, т.е. ΔU = 0.

Если газ получает тепло, то количество теплоты берется со знаком «+»; если газ расширяется, то он совершает положительную работу;

если температура постоянной массы газа растет, то изменение внутренней энергии будет положительным значением, т.е.
Q >0

ΔU >0

A^’>0
Если газ отдает тепло, то количество теплоты берется со знаком «-» ; работа газа при его сжатии отрицательная (при этом внешние силы совершают положительную работу);

если температура постоянной массы газа уменьшается, то изменение внутренней энергии будет отрицательным значением, т.е.
Q <0

ΔU <0

A^’<0
При решении задач на первый закон термодинамики нужно учитывать:

Количество теплоты, переданное газу за цикл, которое определяется суммой количеств теплот, полученных газом в каждом процессе цикла. Количество теплоты, отданное газом за цикл, которое определяется суммой количеств теплот, отданных газом в каждом процессе цикла. Работа газа за цикл определяется алгебраической суммой работ, произведенных газом в каждом процессе цикла. При этом можно определять работу по графику в системе координат Р,V. Работа в этом случае определяется площадью фигуры, ограниченной графиком процесса, ординатами и осью абсцисс, по которой откладывается объем.

Алгоритм решения задач по термодинамике
1. Указать газы, входящие в систему.

2. Отметить начальное и конечное состояние каждого газа, их параметры в каждом состоянии и записать уравнение Менделеева-Клапейрона для каждого состояния газов.

3. Рассмотреть процесс перехода каждого из газов из одного состояния в другое и записать первый закон термодинамики для этого процесса.

Примечание: При необходимости величину совершенной работы определить по площади фигуры, ограниченной графиком процесса на Р,V диаграмме

4. Решить полученную систему уравнений.

5. Проанализировать ответ.
В таблице представлен первый закон термодинамики для изопроцессов с учетом уравнения состояния идеального газа (уравнения Менделеева Клапейрона)

Изотермический процесс	Изобарный процесс	Изохорный процесс	Адиабатный процесс
Т= Const ν= Const	Р= Const ν= Const	V = Const, ν = Const	Q=0
ΔТ = 0 ΔU = 0 Q = A^’ A^’=ν R Т lnV₂/ V₁ A^’=ν RТ ln Р₁/ Р₂ Q = νRТ lnV₂/ V₁ Q = νRТ lnР₁/ Р₂	ΔР = 0 Q = ΔU+A^’ i=3 ΔU = 3/2 νRΔТ A^’= Р ΔV Р ΔV=ν R ΔТ Q = 5/2 ν R ΔТ Q =5/2 Р ΔV	ΔV = 0 A^’= 0 Q = ΔU i=3 ΔU = 3/2 νRΔТ νRΔТ=VΔР Q = 3/2 ν R ΔТ Q = 3/2 V ΔР	0=ΔU+A^’ ΔU= - A^’ ΔU= A, где А- работа внешних сил над газом. ΔU>0, если работу совершают внешние силы; ΔU<0, если работу совершает газ

Тепловая машина (двигатель) служит для преобразования тепловой энергии (внутренней энергии рабочего тела) в механическую энергию. Любая тепловая машина состоит из:

1) нагревателя, от которого рабочее тело получает тепло;

2) холодильника, которому рабочее тело отдает тепло и

3) самого рабочего тела, в качестве которого берется пар, газ, идеальный газ, смесь газов с парами горючего вещества.

Схему тепловой машины можно представить на рисунке:

НАГРЕВАТЕЛЬ

ХОЛОДИЛЬНИК

РАБОЧЕЕ ТЕЛО

Q_Н

Q_Х

А

КПД тепловой машины определяется отношением работы рабочего тела к количеству теплоты, полученной от нагревателя. При этом работа, произведенная рабочим телом за цикл, равна разности количества теплоты, полученной рабочим телом от нагревателя и количества теплоты, отданной рабочим телом холодильнику:

η =

;
η =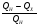

;

Наибольший коэффициент полезного действия имеет идеальный двигатель, работающий по принципу Карно. Цикл идеальной тепловой машины Карно состоит из двух изотерм и двух адиабат. КПД идеальных тепловых машин, работающих по принципу Карно, в отличии от реальных , может определяться через абсолютные температуры нагревателя и холодильника.

η =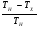

;

При решении задач на тепловые двигатели можно пользоваться следующими правилами:

1. Определить, какими процессами представлен цикл.

2. Определить, на каких участках цикла газ получает тепло от нагревателя.

3. Определить, на каких участках цикла газ отдает тепло холодильнику.

4. Рассчитать полученное и отданное тепло.

5. Определить КПД тепловой машины.

6. Проанализировать полученный результат.

Примечание. КПД теплового двигателя не может превышать 100%.

Рассмотрим решение следующих задач.
Задача 1.

Один моль одноатомного газа, находящегося при нормальных условиях переводят из одного состояния в другое двумя способами:

а) сначала изохорически увеличивая давление в 2 раза, а затем изобарически, увеличивая объем в 2 раза;

б) сначала изобарически увеличивая объем в 2 раза, а затем изохорически, увеличивая давление в 2 раза.

Определите отношение количества теплоты, которые необходимо сообщить

газу в этих процессах.
Представим графики переходов газа из одного состояния в другое для каждого случая:

Рассмотрим случай (а).
1

2

3

Р

V

а)

Переход газа из 1 состояние во 2 происходит изохорно, поэтому работа газом не совершается и
Q_1-2 = ΔU_1-2
Переход газа из 2 состояние в 3 происходит изобарно, поэтому
Q_2-3 = ΔU_2-3+ A^’_2-3
Всего газу нужно сообщить Q _а= Q_1-2+Q_2-3количество теплоты
Q _а= ΔU_1-2+ ΔU_2-3+ A^’_2-3
Учтем, что:

ΔU_1-2 = 3/2 νR(Т₂- Т₁)
ΔU_2-3= 3/2 νR(Т₃– Т₂)
ΔU_1-2+ ΔU_2-3= 3/2 νR(Т₃– Т₁)
A^’_2-3= 2Р₀· ΔV = 2Р₀(2V₀- V₀) = 2Р₀V₀, получим :
Q _а=3/2 νR(Т₃– Т₁) + 2Р₀V₀

Рассмотрим случай (б).

3

Р

V

б)

1

2

Переход газа из 1 состояние во 2 происходит изобарно, поэтому
Q_1-2 = ΔU_1-2+ A^’_1-2
Переход газа из 2 состояние в 3 происходит изохорно, значит газ не совершает работу и поэтому
Q_2-3=ΔU_2-3
Всего газу нужно сообщить Q _б= Q_1-2+Q_2-3количество теплоты
Q _б= ΔU_1-2+ A^’_1-2+ ΔU_2-3
Учтем, что:

ΔU_1-2 = 3/2 ν R(Т₂- Т₁)
ΔU_2-3= 3/2 ν R(Т₃– Т₂)
ΔU_1-2+ ΔU_2-3= 3/2 ν R (Т₃– Т₁)
A^’_1-2= Р₀· ΔV = Р₀(2V₀- V₀) = Р₀V₀, получим :
Q_б= 3/2 ν R (Т₃– Т₁) + Р₀V₀
Запишем уравнения Менделеева-Клапейрона для 1 и 3 состояний газа:
Р₀·V₀= ν R T₁
2Р₀·2V₀= ν R T₃
Откуда видно, что T₃ = 4 T₁ , а

Т₁= Р₀·V₀/ ν R

Тогда
Q_а= 3/2 ν R3Т₁ + 2Р₀V₀= 3/2 ν R3 Р₀·V₀/ ν R+ 2Р₀V₀= 13/2 Р₀V₀;
Аналогично подставляя значения Т₁и Т₃ в Q _б, получим:
Q_б= 11/2 Р₀V₀;
Отношение количества теплоты, которые необходимо сообщить газу в этих процессах

Q_а: Q_б= 13:11
Следует обратить внимание на то, что для расчета изменения внутренней энергии газа в процессах достаточно знать температуру в начальном и конечном состояниях, а в промежуточных состояниях изменение энергии газа можно не рассматривать.

Задача 2.

Один моль идеального одноатомного газа сначала нагрели, о затем охладили до первоначальной температуры 300 К, уменьшив давление в 3 раза (рис.). Какое количество теплоты сообщено газу на участке 1-2? 1

2

3

Р

V

Решение:

Процесс перехода газа 1-2 – изобарное нагревание. Согласно первому закону термодинамики,

Q_1-2 = ΔU_1-2+ A^’_1-2 , где
ΔU_1-2 = 3/2 ν R(Т₂- Т₁) – изменение внутренней энергии газа;
A^’_1-2= Р₁· ΔV – работа газа при изобарном процессе.
Учитывая уравнение Менделеева-Клапейрона, можно выразить
Р₁· ΔV= ν R(Т₂- Т₁), тогда
Q_1-2 = 3/2 ν R(Т₂- Т₁) + ν R(Т₂- Т₁) = 5/2 ν R(Т₂- Т₁).
Запишем уравнение Менделеева-Клапейрона для каждого состояния

Для первого состояния :
Р₁ V₁= ν R T₁ (1)
Для второго состояния:
Р₂ V₂= ν R T₂; Р₁ V₂= ν R T₂(2)

Для третьего состояния:
Р₃V₃= ν R T₃; 3 Р₁ V₂= ν R T₁ (3)

По условию задачи Т₁= 300 К.

Сравнивая (2) и (3), получим, что T₂= 3Т₁.
Q_1-2 = 5/2 ν R(Т₂- Т₁) = 5/2 ν R2Т₁= 5 ν R T₁

Подставляя численные значения, получим Q_1-2 =12,5 кДж.
Задача 3.

Один моль одноатомного идеального газа совершает цикл, изображенный на РV- диаграмме (рис.). Участок 1-2 – изотерма, 2-3 –изобара, 3-1 –адиабата. В изотермическом процессе газ совершает работу, равную А_1-2. Разность температур между состояниями 1 и 3 составляет ΔТ. Определить КПД цикла.
3

1

2

Р

V

0
Решение
Определим процессы цикла и запишем 1 закон термодинамики для каждого из процессов:

1-2 –изотермический; газ получает тепло;

ΔТ = 0
ΔU = 0
Q_1-2 = A^’_1-2
2-3 –изобарный; газ отдает тепло;
Q_2-3 = -ΔU - A^’_2-3
Q_2-3 =- 5/2 ν R ΔТ
3-1-адиабатный процесс; газ не получает и не отдает тепло;

0=ΔU+A^’_3-1
ΔU= - A^’_3-1;

Работа газа за цикл

А^’_1-2-3-1= A^’_1-2- A^’_2-3- A^’_3-1;
Учтем, что

A^’_1-2 известна по условию задачи;
A^’_2-3 = -Р ΔV = ν R (Т₃- Т₂);

A^’_3-1= -3/2 ν R (Т₁- Т₃);

Т₁ = Т₂ ;

Тогда

А^’_1-2-3-1= A^’_1-2 - ν R ΔТ - 3/2 ν R ΔТ;
А^’_1-2-3-1= A^’_1-2 - 5/2 ν R ΔТ;
Так как тело газ получал только на участке 1-2,
Q_Н= Q_1-2 = A^’_1-2

η =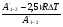

;

Ответ: η = 1-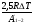

Интерес представляют задачи, в которых рассматриваются не только состояние идеального газа, но и другие процессы. Для примера рассмотрим следующую задачу.
Задача 4.

Воздушный шар объемом 2500 м³ имеет внизу отверстие, через которое воздух в шаре нагревается горелкой до температуры 77⁰С. Этот шар с грузом общей массой 200 кг неподвижно висит в воздухе, температура которого 7⁰С и плотность 1,2 кг/м³. Насколько нужно уменьшить массу груза, чтобы шар, попав в область с температурой воздуха 8⁰С при той же его плотности, продолжал неподвижно висеть? Оболочку шара считать нерастяжимой.(2006,1)
В задаче рассматривается газ (воздух) в воздушном шаре, который сохраняет свой объем (оболочку считать нерастяжимой). Воздушный шар находится в состоянии равновесия. У газа и шара два состояния.

Рассмотрим первое состояние газа.

Параметры состояния газа: V₀ ,T₀, P₀, m

На шар с грузом действуют силы F_Арх., m_газа g, M_груза g.
Во втором состоянии:

Параметры состояния газа V₀, T₀, P_{0 ,}m^’

На шар с грузом действуют силы F_Арх., m’_газа g, M‘_груза g.
Так как шар находится в покое, равнодействующая всех сил, приложенных к шару равна нулю.

Сила Архимеда определяется весом воздуха, заключенного в таком же объеме, как объем шара:

F_Арх.= ρ_возд. gV_шара;
так как плотность воздуха и объем шара по условию не изменяются, то сила Архимеда изменяться не будет при изменении температуры атмосферного воздуха.

Массу газа в шаре можно определить из уравнения состояния газа:

P₀·V₀= νRT₀ ;

где ν – количество вещества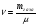

;

где m_газа - масса газа (воздуха).

Отсюда,

. (1)

Давление газа (воздуха) внутри шара равно атмосферному давлению, так как оболочка шара не растягивается.

Р_атм.=Р₀

Для атмосферного воздуха запишем уравнение состояния идеального газа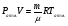

;

Разделив левую и правую части уравнения на V , получим: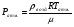

;

Подставим в уравнение (1) вместо Р₀ Р_атм., получим:

.(2)

Запишем условие равновесия воздушного шара в первом и во втором состояниях при разной температуре:
m_газаg + Мg – F_Арх.= 0 ;
где М – масса груза с оболочкой шара при температуре Т_атм.=7⁰С
m_газаg + Мg –_. ρ_возд. gV_шара.= 0 ;
Разделив на g каждое слагаемое, получим:
m_газа + М –_. ρ_возд. V_шара.= 0 ;
Во втором состоянии масса газа (воздуха) в шаре изменилась, так как изменилась температура атмосферного воздуха. Обозначим ее m^’ _газа., а температуру - Т^’_атм . Масса груза, которую может поднять шар, обозначим М’.

Для второго состояния шара условие равновесия запишется:

m ^‘_газа + М^’ –_. ρ_возд. V_шара.= 0 ;

Решив эти уравнения совместно, получим:
ΔМ = m ^‘_газа- m_газа .
Подставив выражения для

m ^‘_газа и m_газа , из (2), получим:

;
После подстановки значений, получим численный ответ: ΔМ =8,6 кг.

Задачи для самостоятельного решения.
V

Р

1

3

2

Рис.1

1. Над идеальным одноатомным газом в количестве 2 моль совершили процесс 1-2-3 (рис.1). Температура газа в состоянии 1 равна 280 К, участок 1-2 является изотермой. Какое количество теплоты было передано газу на участке 2-3?

Р

V

0

2

3

1

Рис.2

2. Над идеальным одноатомным газом в количестве вещества 1 моль совершили процесс 1-2-3-1 (рис.2). Температура газа в состоянии 2 составила 320 К, участок 1-2 является изопроцессом. Какое количество теплоты газ отдал на участке 3 - 1?

Р₀

V

P

1

2

3

V₀

Рис.3
3. Какое количество теплоты подведено к двум молям одноатомного идеального газа при осуществлении процесса 1-2-3 (рис.3), если в состоянии 2 температура его была равна Т₂ = 400 К?
Т

Т₀

2Т₀

4Т₀

Р

3

2

1

3Т₀

4

Рис.4
4. С одним молем идеального одноатомного газа совершают процесс 1-2-3-4, показанный на рисунке 4. Во сколько раз количество теплоты, полученное газом в процессе 1-2-3-4, больше работы газа в этом процессе?

5. Теплоизолированный цилиндр разделен подвижным теплопроводящим поршнем на две части. В одной части цилиндра находится гелий, а в другой – аргон. В начальный момент температура гелия равна 300 К, а аргона – 900 К, и объемы, занимаемые газами, одинаковы. Во сколько раз изменится объем, занимаемый гелием, после установления теплового равновесия, если поршень перемещается без трения? Теплоемкостью цилиндра и поршня пренебречь.

1

2

Р 10⁵ Па

Т, К

300

600

900

1

2

Рис.6

6. Во время опыта объем сосуда с воздухом не менялся, и воздух перешел из состояния 1 в состояние 2 (рис.6). Кран у сосуда был закрыт неплотно, и сквозь него мог просачиваться воздух. Определите отношение N₂/N₁ числа молекул газа в сосуде в конце и начале опыта. Воздух считать идеальным газом.
7. Воздушный шар объемом 2500 м³ с массой оболочки 400 кг имеет внизу отверстие, через которое воздух в шаре нагревается горелкой до температуры 77⁰С. Температура окружающего воздуха 7⁰С. Какой должна быть плотность окружающего воздуха, чтобы шар взлетел вместе с грузом (корзиной и воздухоплавателем) массой 200 кг? Оболочку шара считать нерастяжимой.
8. В цилиндре, закрытом подвижным поршнем, находится газ, который может просачиваться сквозь зазор вокруг поршня. В опыте по изотермическому сжатию газа его объём уменьшился вдвое, а давление газа упало в 3 раза. Во сколько раз изменилась внутренняя энергия газа в цилиндре? (Газ считать идеальным)
9,10. Один моль идеального одноатомного газа сначала охладили, а затем нагрели до первоначальной температуры 300 К, увеличив объём газа в 3 раза. Какое количество теплоты отдал газ на участке 1-2?
V

Р

1

2

3

Рис.9

Т

Р

2

3

1

Рис.10
Р

3Т₀

1

3

2

Т₀

Т

Рис.11

11. Один моль одноатомного газа совершает процесс 1-2-3 (см. рис.11). Т₀=100К. На участке 2-3 к газу подводят 1 кДж теплоты. Найдите отношение работы А_1-2-3,совершенной газом в ходе всего процесса к полному количеству теплоты Q_1-2-3, подведенной к газу.