Урока по алгебре в 8 классе по теме: «Квадратные корни. Арифметический квадратный корень»
 Скачать 57.79 Kb.
|
Конспект урока по алгебре в 8 классе по теме: «Квадратные корни. Арифметический квадратный корень». Разработал учитель математики Красногорского района МБОУ Увельской ООШ Белоус Наталья Петровна Цели:
Задачи:
Тип урока: урок изучение нового материала Необходимое техническое оборудование: компьютер, мультимедийный проектор, экран, презентация, карточки. Ход урока I. Организационный момент.
Урок начинается с эпиграфа «Дорогу осилит идущий». (сл. 2) - В справдивости этих слов ,ребята, мы убедимся на нашем сегодняшнем уроке. Прежде чем приступить к новой теме урока, давайте вспомним с вами пройденный материал. II. Проверка знаний, умений учащихся по ранее изученному материалу.
- Рассмотрим это в виде рисунка. (сл.3) II. Актуализация знаний. Задание 1: Установить к какому множеству относится число. Выполняется устно. (сл. 4) Задание 2: Выяснить, какие из высказываний истинные (устно) (сл. 5). Задание 3: Представьте в виде бесконечной периодической дроби письменно (сл. 6). Проверь себя (сл. 7) Задание 4: Отметьте верные утверждения (сл. 8). Проверь себя (сл. 9). Задание 5: Вычислите устно.        
III. Постановка целей урока, сообщение темы (сл. 11-12). - Параллельно нашей главной теме, я хочу обратить ваше внимание на не мене важную тему. Которая должна являться самой главной целью нашей жизни. А какой именно, вы узнаете, расшифровав данную таблицу (сл. 13). Для того, чтобы расшифровать слово в ней, вам достаточно вспомнить таблицу умножения. Например, из произведения каких чисел состоит число 42. Соединив эти цифры вместе мы получим нужную нам букву. В результате должно получиться слово здоровье (сл. 14). Здоровье - это бесценный дар, который преподносит человеку природа. Без него очень трудно сделать жизнь человека интересной и счастливой. IV. Ознакомление с новым материалом З а д а н и е (сл. 15): вставить в пустые клеточки числа, чтобы равенства были верными: Определение (сл. 16): Квадратным корнем из числа а называют число, квадрат которого равен а. Число b называют квадратным корнем из числа а, если b  = а.Задание (сл. 16): выяснить, является ли число n квадратным корнем из числа т, если: а) n = 5, т = 25; в) n = 0,3, т = 0,9; б) n = –7, т = 49; г) n = 6, т = –36. Определение (сл. 17):  Задание (сл. 18): вычислить 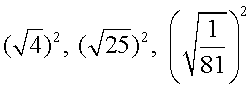 Определение (сл. 19): При любом а, при котором выражение √а имеет смысл, верно равенство: (√а) = а, где а ≥ 0Немного истории (сл. 20-21): Обратим внимание на совпадение в терминах – квадратный корень и корень уравнения. Это совпадение не случайно. Уравнения вида х =а исторически были первыми сложными уравнениями, и их решения были названы корнями по метафоре, что из стороны квадрата, как из корня, вырастает сам квадрат. В дальнейшем термин «корень» стал употребляться и для произвольных уравнений.Название «радикал» тоже связано с термином «корень»: по-латыни корень – radix (он же редис – корнеплод). Также слово «радикальный» в русском языке является синонимом слова «коренной». Происхождение же символа связывают с написанием латинской буквы r. Радикальные изменения, те. коренные изменения. V. Первичное осмысление и закрепление нового материала - А сейчас мы с вами немножко поиграем в игру поле чудес (сл. 22-23). При выполнении № 300, № 301, № 306 вам необходимо отыскать ответ в данной таблице и записать рядом с ответом соответствующую букву. В результате мы получим с вами набор слов, которые тесно связаны со здоровьем. (задание выполняется самостоятельно, с последующей проверкой с доской) - У нас получились слова отсутствие вредных привычек. Вредные привычки – это различные виды отклонения от здорового образа жизни. - Какие три самые главные Вредные привычки мы знаем? (сл. 24,25,26) А к полезным привычкам что мы можем отнести? Питание, физическая активность, закаливание (сл. 27-30). VI. Самостоятельная работа учащихся Математический диктант, с последующей взаимопроверкой по шаблону 1.Как называют действие нахождения квадратного корня из числа? ( извлечение квадратного корня) 2.Объясните, почему верно или неверно равенство: 1) √0,64 = 0,8 (равенство верно, т.к. 0,8>0 и 0,82=0,64 ) 2) √0,25 = - 0,5 (равенство неверно, т.к. - 0,5<0 ) 3.В равенствах п.2 1) и 2) подчеркните подкоренные выражения ( 1)√0,64 = 0,8 2) √0,25 = - 0,5 ) 4.При каких значениях x имеет смысл выражение √x? ( x ≥ 0 ) 5.Вычислить арифметический квадратный корень из числа: √900 (√900=30) √0,36 (√0,36=0,6) (√5)2 ( (√5)2 = 5) √ (0,04)2 (√ (0,04)2 =0,04 ) √ (-2)2 (√ (-2)2 = 2) По окончании работы ребята оценивают свою работу по следующим критериям: а) Решил сам без ошибок и помог товарищу – “5” б) Решил сам, но консультировался у товарища – “4” в) Решал с помощью тетради или учебника – “3” VII. Итоги урока (сл. 31-32).
Оценка результатов урока учителем. VIII. Домашнее задание (сл. 33): п.12 (выучить правила); № 302 (в); № 306 (г); № 304; из повторения: № 317 – сильным учащимся - Сегодня мы осилили путь и убедились в правдивости высказывания «Дорогу осилит идущий». - «Знания способны весь мир перевернуть. Там где есть знание, всегда найдется путь!». Так пусть ваше желание учиться с каждым днем становится сильнее. (сл. 34) - ЗДОРОВЬЯ ВАМ КРЕПКОГО, СЧАСТЬЯ И ДОЛГОЛЕТИЯ! (сл. 35). |
то такое арифметический квадратный корень из числа а?
сегда ли верно равенство = а?