|
" Метод координат в пространстве"
Зачетная работа по теме:“ Метод координат в пространстве“.
Вам предлагается 10 задач. Каждая из задач 1-6 оценивается в 0,5 балла, каждая из задач 7-8 оценивается в 1 балл, каждая из задач 9-10 оценивается в 2 балла.
Вариант1.
Даны векторы  , , 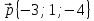 . Будут ли коллинеарны векторы . Будут ли коллинеарны векторы 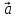 + 2 + 2  и и  ? ?
Даны точки A, B, C, причем 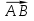 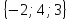 и и 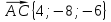 . Лежат ли эти точки на одной прямой? . Лежат ли эти точки на одной прямой?
Вычислить длину вектора  = 2 = 2 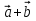 , если , если 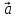 = =  + +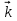 и и  =2 =2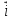 + + -3 -3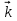 . .
Доказать, что векторы 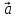 = 5 = 5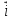 -3 -3 +3 +3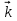 и и  = 3 = 3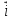 +4 +4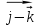 взаимно перпендикулярны. взаимно перпендикулярны.
Даны точки A (0;-1;2), B (-1;4;3), C (-2;1;0) и D (-1;0;3). Найти координаты и длину вектора  = =
Даны векторы  и и  , причем , причем  =1, =1, 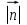 =2, а угол между ними =2, а угол между ними  . Найти ( . Найти ( + + ) ) . .
Дана точка M (3;-1;-2). Найти координаты точки, симметричной точке М относительно начала координат, оси ординат и плоскости Oyz.
Куб ABCD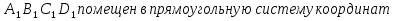 . Точка A (2;-2;0). Найдите координаты остальных вершин куба и найдите расстояние от точки D до прямой . Точка A (2;-2;0). Найдите координаты остальных вершин куба и найдите расстояние от точки D до прямой 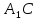 . .
В правильной четырехугольной пирамиде SABCD, все ребра которой равны 1, точки E и F- середины ребер SB и SC соответственно. Найдите косинус угла между прямыми AE и BF.
В правильной четырехугольной призме ABCD 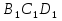 стороны основания равны 2, а боковые ребра 3. На ребре A стороны основания равны 2, а боковые ребра 3. На ребре A отмечена точка E так, что отмечена точка E так, что 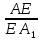 = =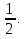 Найдите угол между плоскостями ABC и BE Найдите угол между плоскостями ABC и BE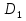 . .
И конечно, желаем вам успешно справиться с работой, милые детишки!
|
|
|
 Скачать 17.91 Kb.
Скачать 17.91 Kb. ,
, 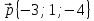 . Будут ли коллинеарны векторы
. Будут ли коллинеарны векторы 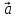 + 2
+ 2  и
и  ?
? 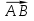
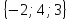 и
и 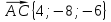 . Лежат ли эти точки на одной прямой?
. Лежат ли эти точки на одной прямой? = 2
= 2 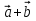 , если
, если  +
+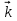 и
и 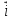 +
+ -3
-3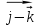 взаимно перпендикулярны.
взаимно перпендикулярны.
 , причем
, причем  =1,
=1, 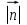 =2, а угол между ними
=2, а угол между ними  . Найти (
. Найти (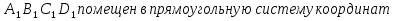 . Точка A (2;-2;0). Найдите координаты остальных вершин куба и найдите расстояние от точки D до прямой
. Точка A (2;-2;0). Найдите координаты остальных вершин куба и найдите расстояние от точки D до прямой 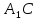 .
.
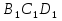 стороны основания равны 2, а боковые ребра 3. На ребре A
стороны основания равны 2, а боковые ребра 3. На ребре A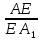 =
=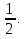 Найдите угол между плоскостями ABC и BE
Найдите угол между плоскостями ABC и BE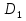 .
.