Тренировочная работа №1 Вариант1 Часть 1

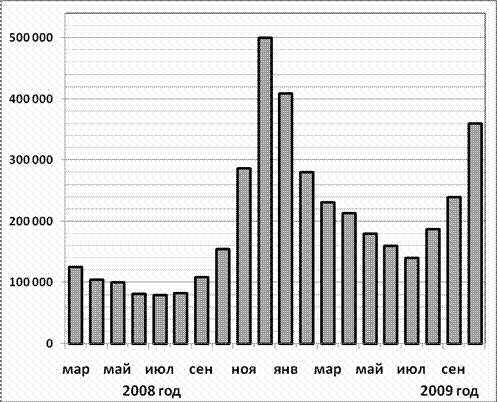В4. При строительстве сельского дома можно использовать один из двух типов фундамента: каменный или бетонный. Для каменного фундамента необходимо 11 тонн природного камня и 12 мешков цемента. Для бетонного фундамента необходимо 8 тонн щебня и 57 мешков цемента. Тонна камня стоит 1450 рублей, щебень стоит 630 рублей за тонну, а мешок цемента стоит 240 рублей. Сколько рублей будет стоить материал для фундамента, если выбрать наиболее дешевый вариант?

В5. Найдите корень уравнения: В ответе запишите наибольший отрицательный корень.

В6. В тупоугольном треугольнике ABC , CH  — высота, , . Найдите синус угла ABC.

В7. Найдите значение выражения .

В8. На рисунке изображен график производной функции , определенной на интервале . Найдите точку экстремума функции на отрезке .



В9. Шар вписан в цилиндр. Площадь поверхности шара равна 39. Найдите площадь полной поверхности цилиндра.

В10. На олимпиаде по русскому языку участников рассаживают по трём аудиториям. В первых двух по 100 человек, оставшихся проводят в запасную аудиторию в другом корпусе. При подсчёте выяснилось, что всего было 400 участников. Найдите вероятность того, что случайно выбранный участник писал олимпиаду в запасной аудитории.

В11. Объем параллелепипеда 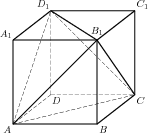равен . Найдите объем треугольной пирамиды .



В12. Для поддержания навеса планируется использовать цилиндрическую колонну. Давление P (в паскалях), оказываемое навесом и колонной на опору, определяется по формуле , где  кг — общая масса навеса и колонны, D — диаметр колонны (в метрах). Считая ускорение свободного падения  м/с, а , определите наименьший возможный диаметр колонны, если давление, оказываемое на опору, не должно быть больше 500000 Па. Ответ выразите в метрах.

В13. Первая труба пропускает на 2 литра воды в минуту меньше, чем вторая. Сколько литров воды в минуту пропускает вторая труба, если резервуар объемом 513 литров она заполняет на 8 минут быстрее, чем первая труба заполняет резервуар объемом 675 литров?

В14. Найдите наименьшее значение функции на отрезке .

Часть 2

С1. Дано уравнение: cos () = cos x

а) Решите уравнение.

б) Укажите корни уравнения, принадлежащие отрезку .

С2. В кубе АВСDАВСDнайдите тангенс угла между прямой АА и плоскостью ВСD.

С3. Решите неравенство:.

С4. Дана трапеция АВСD, основания которой ВС=44, АD=100, АВ=СD=35. Окружность, касающаяся прямых АD и АС, касается стороны СD в точке К. Найдите длину отрезка СК.

С5.Найдите все значения а, при каждом из которых решения неравенства образуют отрезок длины 1.

С6. Найдите все решения в целых числах .

Тренировочная работа №1

Вариант2

Часть 1

В1. Тетрадь стоит 40 рублей. Какое наибольшее число таких тетрадей можно будет купить на 500 рублей после понижения цены на 25%?

В2. На диаграмме показано количество запросов со словом СНЕГ, сделанных на поисковом сайте Yandex.ru во все месяцы с марта 2008 по октябрь 2009 года. По горизонтали указываются месяцы, по вертикали — количество запросов за данный месяц. Определите по диаграмме, сколько было таких месяцев, когда было сделано более 200 000 запросов со словом СНЕГ.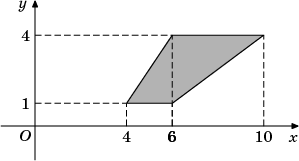

В4. Клиент хочет арендовать автомобиль на сутки для поездки протяженностью 600 км. В таблице приведены характеристики трех автомобилей и стоимость их аренды. Помимо аренды клиент обязан оплатить топливо для автомобиля на всю поездку. Какую сумму заплатит клиент за аренду и топливо, если выберет самый дешевый вариант?

Автомобиль	Топливо	Расход топлива на 100 км	Арендная плата за 1 сутки
1.	Дизельное	4	3600
2.	Бензин	9	3000
3.	Газ	10	3200

Цена дизельного топлива 16,5 руб. за литр, бензина 17,5 руб. за литр, газа 15,5 руб. за литр.

В5. Найдите корень уравнения: В ответе запишите наибольший отрицательный корень.

В6. В тупоугольном треугольнике ABC , CH  — высота, , . Найдите синус угла ABC.

В7. Найдите значение выражения .

В8. На рисунке изображен график производной функции , определенной на интервале . Найдите точку экстремума функции на отрезке .



В9. Около конуса описана сфера (сфера содержит окружность основания конуса и его вершину). Центр сферы находится в центре основания конуса. Радиус сферы равен . Найдите образующую конуса.

В10. В классе 6 учащихся, среди них два друга — Олег и Сергей. Класс случайным образом разбивают на 2 равные группы. Найдите вероятность того, что Олег и Сергей окажутся в одной группе.

В11. Объем параллелепипеда 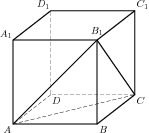равен . Найдите объем треугольной пирамиды .



В12. Для поддержания навеса планируется использовать цилиндрическую колонну. Давление P (в паскалях), оказываемое навесом и колонной на опору, определяется по формуле , где  кг — общая масса навеса и колонны, D — диаметр колонны (в метрах). Считая ускорение свободного падения  м/с, а , определите наименьший возможный диаметр колонны, если давление, оказываемое на опору, не должно быть больше 600000 Па. Ответ выразите в метрах.

В13. Первая труба пропускает на 4 литра воды в минуту меньше, чем вторая. Сколько литров воды в минуту пропускает вторая труба, если резервуар объемом 696 литров она заполняет на 5 минут быстрее, чем первая труба заполняет резервуар объемом 725 литров?

В14. Найдите наименьшее значение функции на отрезке .

Часть 2

С1. . Дано уравнение: sin () = cos x

а) Решите уравнение

б) Укажите корни уравнения, принадлежащие отрезку

С2. В кубе АВСDАВСDнайдите тангенс угла между прямой АС и плоскостью ВСС.

С3. Решите неравенство:.

С4. Дана трапеция АВСD, основания которой ВС=44, АD=100, АВ=СD=35. Окружность, касающаяся прямых АD и АС, касается стороны СD в точке К. Найдите длину отрезка СК.

С5.Найдите все значения а, при каждом из которых решения неравенства образуют отрезок длины 1.

С6. Найдите все решения в целых числах .