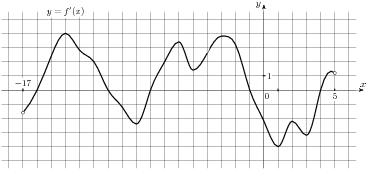|
Прямая параллельна касательной к графику функции. Найдите абсциссу точки касания
ЕГЭ В 8
Вариант № 2
Прямая 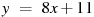 параллельна касательной к графику функции параллельна касательной к графику функции 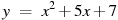 . Найдите абсциссу точки касания. . Найдите абсциссу точки касания.
Прямая 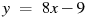 является касательной к графику функции является касательной к графику функции 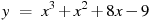 . Найдите абсциссу точки касания. . Найдите абсциссу точки касания.
На рисунке изображен график функции 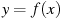 , определенной на интервале , определенной на интервале 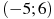 . Определите количество целых точек, в которых производная функции положительна. . Определите количество целых точек, в которых производная функции положительна.

На рисунке изображен график функции 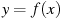 , определенной на интервале , определенной на интервале 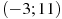 . Найдите количество точек, в которых касательная к графику функции параллельна прямой . Найдите количество точек, в которых касательная к графику функции параллельна прямой 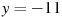 . .

На рисунке изображен график функции 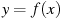 , определенной на интервале , определенной на интервале 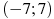 . Найдите сумму точек экстремума функции . Найдите сумму точек экстремума функции 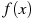 . .

На рисунке изображен график 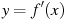 — производной функции — производной функции 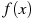 , определенной на интервале , определенной на интервале 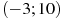 . В какой точке отрезка . В какой точке отрезка ![[0; 4 ]](346097_html_m1c4e5278.png) 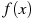 принимает наибольшее значение? принимает наибольшее значение?

На рисунке изображен график 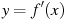 — производной функции — производной функции 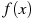 , определенной на интервале , определенной на интервале 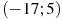 . Найдите количество точек максимума функции . Найдите количество точек максимума функции 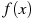 , принадлежащих отрезку , принадлежащих отрезку ![[-15;0]](346097_html_5d6237c3.png) . .
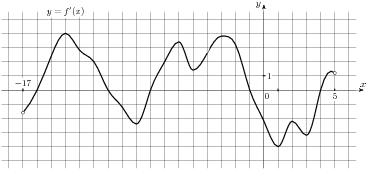
На рисунке изображен график 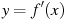 — производной функции — производной функции 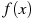 , определенной на интервале , определенной на интервале 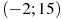 . Найдите количество точек экстремума функции . Найдите количество точек экстремума функции 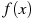 , принадлежащих отрезку , принадлежащих отрезку ![[2;10]](346097_html_414af395.png) . .

На рисунке изображен график 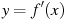 — производной функции — производной функции 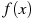 , определенной на интервале , определенной на интервале 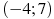 . Найдите промежутки убывания функции . Найдите промежутки убывания функции 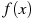 . В ответе укажите сумму целых точек, входящих в эти промежутки. . В ответе укажите сумму целых точек, входящих в эти промежутки.
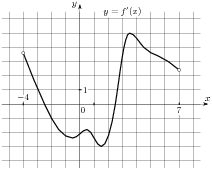
На рисунке изображен график 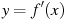 — производной функции — производной функции 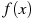 , определенной на интервале , определенной на интервале 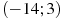 . Найдите промежутки убывания функции . Найдите промежутки убывания функции 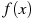 . В ответе укажите длину наибольшего из них. . В ответе укажите длину наибольшего из них.

На рисунке изображен график 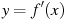 — производной функции — производной функции 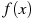 , определенной на интервале , определенной на интервале 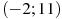 . Найдите количество точек, в которых касательная к графику функции . Найдите количество точек, в которых касательная к графику функции 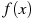 параллельна прямой параллельна прямой 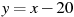 или совпадает с ней. или совпадает с ней.

На рисунке изображен график 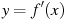 — производной функции — производной функции 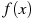 , определенной на интервале , определенной на интервале 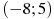 . Найдите точку экстремума функции . Найдите точку экстремума функции 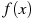 , принадлежащую отрезку , принадлежащую отрезку ![[-7; 0 ]](346097_html_m17ed98e2.png) . .

На рисунке изображены график функции 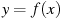 и касательная к нему в точке с абсциссой и касательная к нему в точке с абсциссой  . Найдите значение производной функции . Найдите значение производной функции 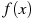 в точке в точке  . .

На рисунке изображен график функции 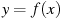 , определенной на интервале , определенной на интервале 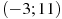 . Найдите количество точек, в которых производная функции . Найдите количество точек, в которых производная функции 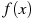 равна 0 . равна 0 .

Прямая 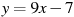 является касательной к графику функции является касательной к графику функции 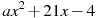 . Найдите a. . Найдите a.
Прямая 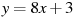 является касательной к графику функции является касательной к графику функции 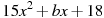 . Найдите b, учитывая, что абсцисса точки касания меньше 0. . Найдите b, учитывая, что абсцисса точки касания меньше 0.
Прямая 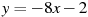 является касательной к графику функции является касательной к графику функции 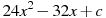 . Найдите c. . Найдите c.
Материальная точка движется прямолинейно по закону 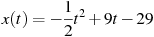 , где , где  — расстояние от точки отсчета в метрах, — расстояние от точки отсчета в метрах, 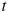 — время в секундах, измеренное с начала движения. Найдите ее скорость (в метрах в секунду) в момент времени — время в секундах, измеренное с начала движения. Найдите ее скорость (в метрах в секунду) в момент времени 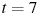 с. с.
На рисунке изображен график функции 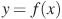 и отмечены точки -2, -1, 3, 4. В какой из этих точек значение производной наименьшее? В ответе укажите эту точку. и отмечены точки -2, -1, 3, 4. В какой из этих точек значение производной наименьшее? В ответе укажите эту точку.
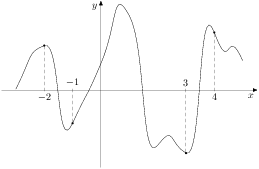
На рисунке изображён график функции 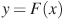 — одной из первообразных некоторой функции — одной из первообразных некоторой функции 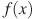 , определённой на интервале , определённой на интервале 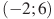 . Пользуясь рисунком, определите количество решений уравнения . Пользуясь рисунком, определите количество решений уравнения  на отрезке на отрезке ![[-1;5]](346097_html_m7bc94f20.png) . .

На рисунке изображён график некоторой функции 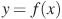 (два луча с общей начальной точкой). Пользуясь рисунком, вычислите (два луча с общей начальной точкой). Пользуясь рисунком, вычислите  , где , где 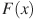 — одна из первообразных функции — одна из первообразных функции 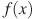 . .

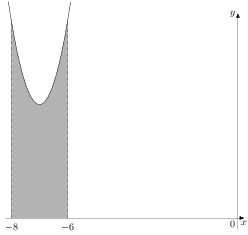
На рисунке изображён график некоторой функции 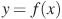 . Функция . Функция  — одна из первообразных функции — одна из первообразных функции 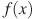 . Найдите площадь закрашенной фигуры. . Найдите площадь закрашенной фигуры.
 |
|
|
 Скачать 39.97 Kb.
Скачать 39.97 Kb.