Уроков геометрии в 7 классе по теме «Первый признак равенства треугольников»
 Скачать 152.66 Kb. Скачать 152.66 Kb.
|
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| № п/п | Этапы урока | Слайд презентации |
| ||
| | Сообщение темы и целей урока. На сегодняшнем уроке мы продолжим разговор о треугольниках и выясним, каким образом можно установить их равенство. Но для начала необходимо вспомнить определение треугольника и его элементов. | Слайд 1.  |
| ||
| |
Как называются элементы треугольника?
| Слайд 2. 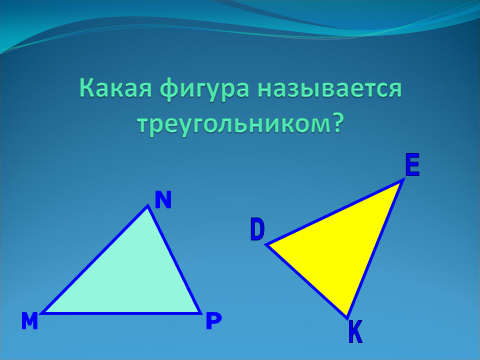 |
| |
| Слайд 3. 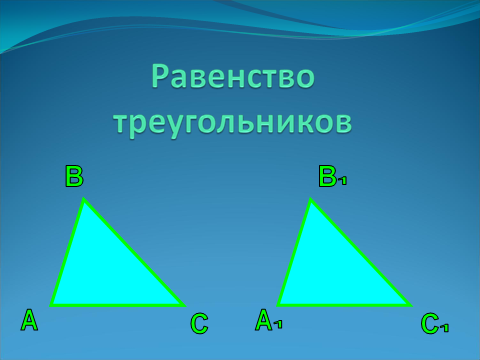 |
| |
ΔAPC = ΔMFB, P = M, FB = 17см, А = F, РС = 23 см. Найдите АС и МВ. Ответ. В равных треугольниках все элементы соответственно равны, значит, АС = FB = 17 см, МВ = ВС = 23 см. | Слайд 4. 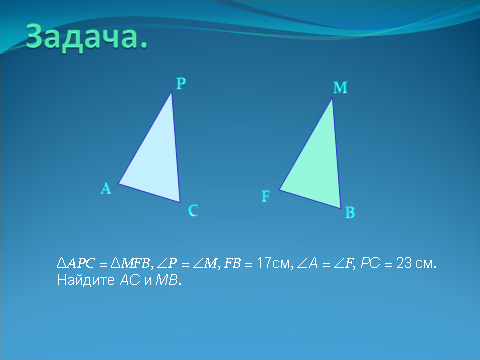 |
| |
Ответ: с помощью способа наложения.
Ответ: при сравнении земельных участков треугольной формы нельзя использовать способ наложения. В тех случаях, когда невозможно воспользоваться способом наложения вывод о равенстве треугольников делают на основании соответствующих признаков. С первым признаком равенства треугольников вы познакомитесь на сегодняшнем уроке. Этот признак сформулирован в виде утверждения, справедливость которого будет установлена путем рассуждений. | Слайд 5. 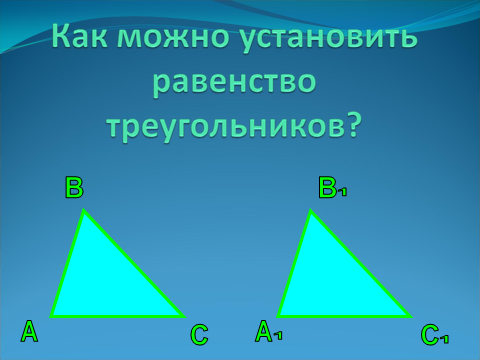 |
| ||
| |
Какие теоремы вам уже известны? (Свойства смежных и вертикальных углов) Любая теорема состоит из условия и заключения. Как вы считаете, что могут означать словосочетания «условие теоремы», «заключение теоремы»? (Условие – это уже известные факты, о которых говорится в теореме, а заключение – это то, что нужно получить, доказать) Выделите условие и заключение в теореме выражающей свойство вертикальных углов. (Если углы вертикальные, то они равны) Условие Заключение Мы с вами должны сформулировать теорему, выражающую признак равенства треугольников. Что такое признак? (Примета, знак, по которому можно определить что-либо. Отличительное качество чего-либо) Давайте попробуем определить, какие «приметы» или «знаки» помогут нам ответить на вопрос: равны ли два треугольника или нет. Для этого вернемся к вопросу: как можно установить равенство треугольников? | Слайд 6.  |
| |
Оказывается не нужно проверять равенство всех сторон и углов одного треугольника сторонам и углам другого треугольника. Достаточно установить лишь часть из этих равенств. Рассмотрите рисунок и ответьте, равны ли ΔАВС и ΔАСD, если у них АС – общая? (Треугольники не равны, значит для того, чтобы установить равенство двух треугольников недостаточно выделить в них только по одному равному элементу) | Слайд 7. 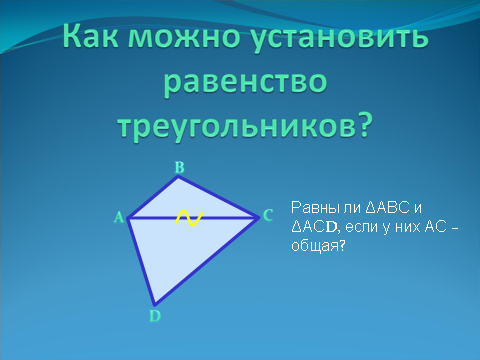 |
| |
| Слайд 8.  |
| |
Если две стороны и угол между ними одного треугольника соответственно равны двум сторонам и углу между ними другого треугольника, то такие треугольники равны. Выполните чертеж и отметьте равные элементы треугольников. Выделите в теореме условие и заключение. Дано (условие): ΔАВС и ΔА1В1С1; АВ = А1В1; АС = А1С1; А = А1. Доказать, что (заключение) Δ АВС = Δ А1В1С1. Доказательство (проводит учитель, используя модель треугольника). Так как А = А1, то ΔАВС можно наложить на Δ А1В1С1 так, что вершина А совместиться с вершиной А1, а стороны АВ и АС наложатся соответственно на лучи А1В1 и А1С1. Поскольку АВ = А1В1, АС = А1С1, то сторона АВ совместится со стороной А1В1, а сторона АС – со стороной А1С1, то есть совместятся точки В и В1, С и С1. Следовательно, совместятся стороны ВС и В1С1. Итак, Δ АВС и Δ А1В1С1 полностью совместятся, значит, они равны. | Слайд 9. 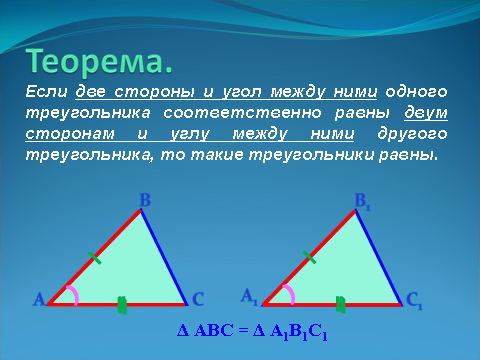 |
| ||
| | Первый признак равенства треугольников удобнее называть признаком равенства треугольников по двум сторонам и углу между ними. Рассмотрим задачу, в решении которой используется первый признак равенства треугольников. Задача. Необходимо измерить расстояние между пунктами А и В, находящимися в труднодоступных местах. | Слайд 10.  |
| | Решение. Чтобы измерить расстояние между точками А и В на местности необходимо провести два отрезка АС и BD, пересекающиеся в их общей середине – точке О. Рассмотрим ΔАОВ и ΔDOC. АО = ОС, ВО = OD, АОВ = DOC (по свойству вертикальных углов), следовательно, ΔАОВ = ΔDOC (по двум сторонам и углу между ними). Из равенства треугольников следует, что АВ = DC. Значит, измерив длину отрезка DC мы определим расстояние между точками А и В. | Слайд 11.  Слайд 12. 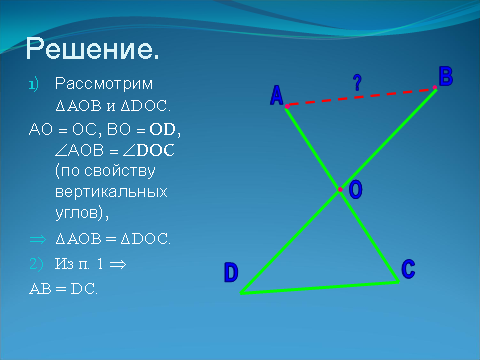 |
| ||
| |
| |
Урок второй.
Тип урока. Урок формирования и совершенствования знаний
Цели и задачи урока:
развивать умение выделять соответственно равные элементы данных треугольников по готовым чертежам;
совершенствовать навыки решения задач на применение первого признака равенства треугольников;
развивать воображение, память, внимание, умение анализировать, сравнивать, обобщать;
воспитывать самостоятельность, трудолюбие, аккуратность.
Оборудование: мультимедийный проектор, компьютер, карточки с текстами самостоятельной работы.
Ход урока.
| № п/п | Этапы урока | Слайд презентации |
| ||
| | Сообщение темы и целей урока. Сегодня вы познакомились с первым признаком равенства треугольников. Теперь необходимо научиться применять эту теорему при решении задач. | Слайд 1.  |
| ||
| | Сформулируйте первый признак равенства треугольников. Какие равные элементы нужно выделить в двух треугольниках, чтобы установить их равенство? | Слайд 9.  |
| ||
| | Задача 2. Докажите, что треугольники, изображенные на рисунке, равны. | Слайд 13. 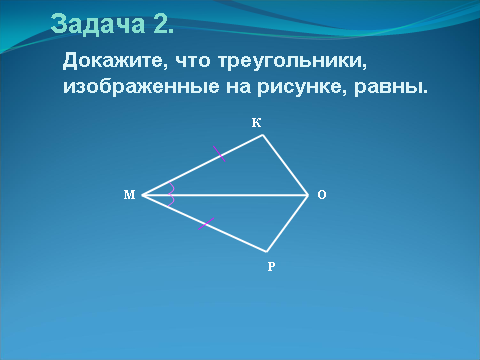 |
| | Задача 3. Найдите по рисунку величину угла АDС и длину стороны ВС. | Слайд 14. 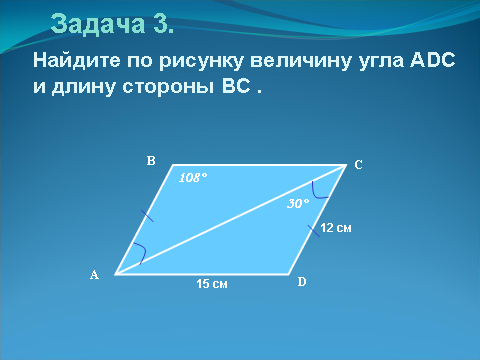 |
| | Задача 4. 1 = 2, KF = ED, H – середина КЕ. Докажите, что ΔKFE = ΔEPH. | Слайд 15. 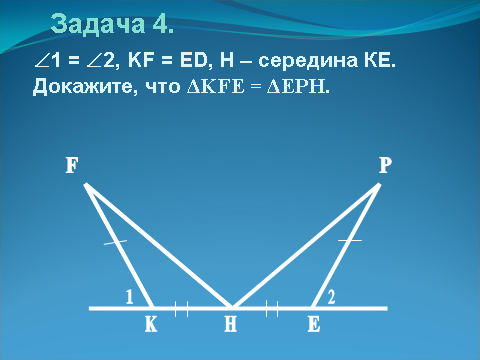 |
| ||
| | Учащиеся устно выполняют задания теста. Проверка осуществляется после выполнения каждого задания. 1. Какой элемент треугольника ABC необходимо задать, чтобы треугольники ABC и DEF были равны по первому признаку равенства треугольников? а) ÐС=50° б) АС= 7 см в) ÐВ=50° 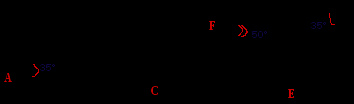 | Слайд 16. 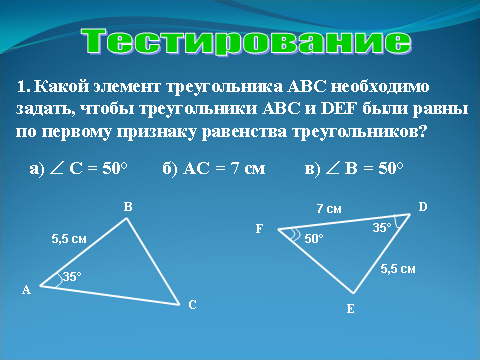 |
| | 2. В треугольниках АВС и DEF АВ = DE, ВС = EF, ÐС =Ð F. Можно ли на основании первого признака равенства треугольников утверждать, что эти тре угольники равны? а) Да. б) Нет. 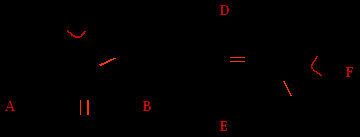 | Слайд 17. 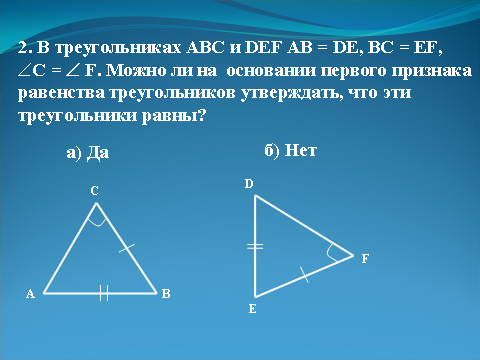 |
| | 3. В треугольниках ABC и DEF АВ = DE, ВС = EF. Какое еще условие должно быть выполнено, чтобы эти треугольники были равны по первому признаку ра венства треугольников? а) Ð A =Ð D. б) ÐС = ÐF. в) ÐВ = ÐЕ. г) АС = DF. | Слайд 18. 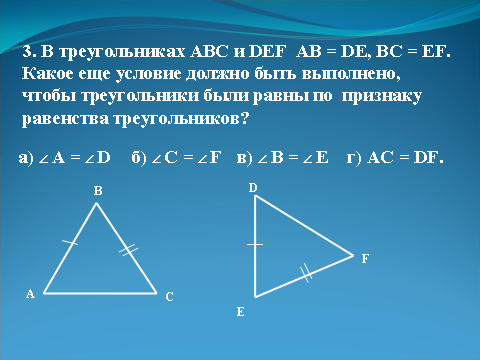 |
| | 4. Треугольники ABC и ACD равны. Найдите угол CAD. а) Ð CAD = 50° б) Ð CAD = 30°. 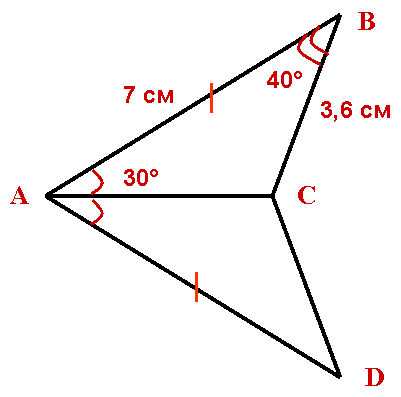 | Слайд 19. 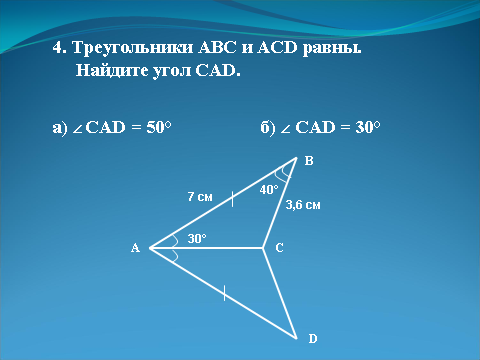 |
| | 5. Можно ли утверждать, что треугольники, изображенные на рисунке, равны? а) Да. б) Нет. 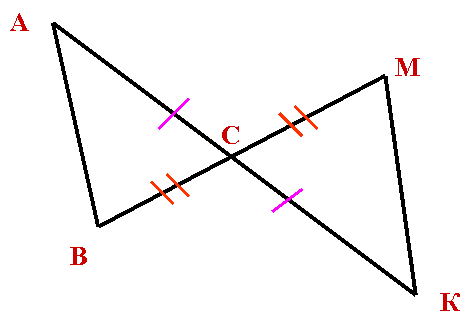 | Слайд 20. 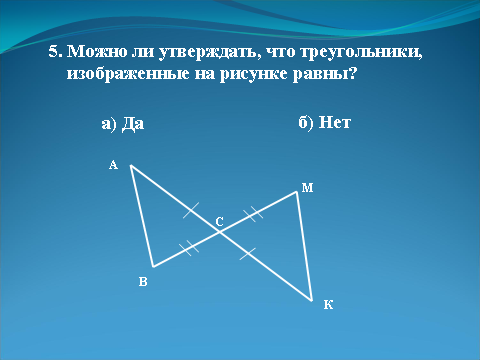 |
| ||
| | Гимнастика для глаз Закройте глаза на несколько секунд, сильно напрягая глазные мышцы, затем раскройте их, рас слабив мышцы. Повторите 3-4 раза. Посмотрите на переносицу и задержите взор. Затем посмотрите вдаль. Повторите 3-4 раза. Медленно наклоняйте голову: вперед-влево-вправо-назад. Повторите 3-4 раза. Поморгайте несколько раз глазами, не напря гая мышц. Сделайте глубокий вдох и медленный выдох. | Слайд 21.  |
| ||
| | Задания самостоятельной работы выполняются на карточках с готовыми чертежами. ВАРИАНТ 1 1)Докажите равенство треугольников ADC и ABC, изображенных на рисунке, если AD = АВ и Ð DAC= Ð CAB. 2)Найдите углы ADC и ACD, если Ð ACB = 38°, Ð ABC = 102°. 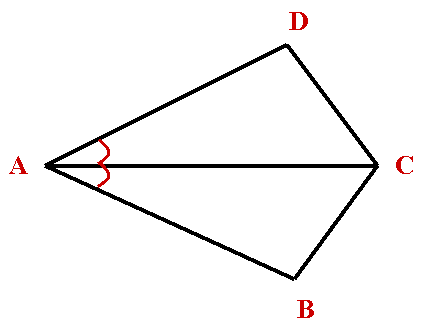 ВАРИАНТ 2 1)Докажите равенство треугольников ADC и ABC, изображенных на рисунке, если AD = ВС и Ð DAC = Ð ВСА. 2)Найдите углы ADC и ACD, если Ð ABC = 108°, Ð ВАС =32°. 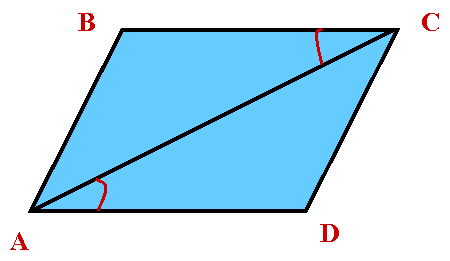 | Слайд 22. 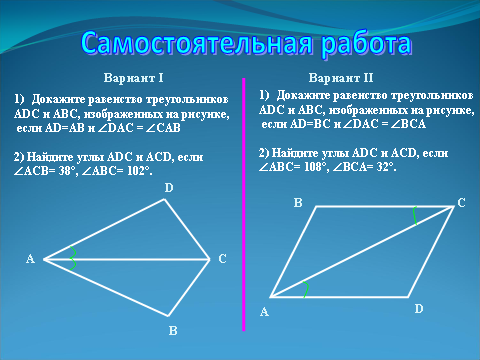 |
| ||
| | п.15, № 93, № 96 | Слайд 23.  |
| ||
| |
| Слайд 24.  |
Какой элемент треугольника АВС необходимо
задать, чтобы треугольники АВС и DEF были равны
по первому признаку равенства треугольников?
А
В
С
F
D
E
5,5 см
5,5 см
7 см
35°
35°
50°
а) С = 50°
б) АС = 7 см
в) В = 50°
Какой элемент треугольника АВС необходимо
задать, чтобы треугольники АВС и DEF были равны
по первому признаку равенства треугольников?
А
В
С
F
D
E
5,5 см
5,5 см
7 см
35°
35°
50°
а) С = 50°
б) АС = 7 см
в) В = 50°
Какой элемент треугольника АВС необходимо
задать, чтобы треугольники АВС и DEF были равны
по первому признаку равенства треугольников?
А
В
С
F
D
E
5,5 см
5,5 см
7 см
35°
35°
50°
а) С = 50°
б) АС = 7 см
в) В = 50°
Какой элемент треугольника АВС необходимо
задать, чтобы треугольники АВС и DEF были равны
по первому признаку равенства треугольников?
А
В
С
F
D
E
5,5 см
5,5 см
7 см
35°
35°
50°
а) С = 50°
б) АС = 7 см
в) В = 50°
в) В = 50°
б) АС = 7 см
а) С = 50°
50°
35°
35°
7 см
5,5 см
5,5 см
E
D
F
С
В
А
в) В = 50°
б) АС = 7 см
а) С = 50°
50°
35°
35°
7 см
5,5 см
5,5 см
E
D
F
С
В
А
в) В = 50°
б) АС = 7 см
а) С = 50°
50°
35°
35°
7 см
5,5 см
5,5 см
E
D
F
С
В
А
в) В = 50°
б) АС = 7 см
а) С = 50°
50°
35°
35°
7 см
5,5 см
5,5 см
E
D
F
С
В
А
в) В = 50°
б) АС = 7 см
а) С = 50°
50°
35°
35°
7 см
5,5 см
5,5 см
E
D
F
С
В
А


