|
| Список всех пионерских лагерей Линтас Тур. www.lintastour.ru | Тест 1 Аксиомы стереометрии
Тест 1
Аксиомы стереометрии
Вариант 1
1
|
Точка Р лежит на прямой МN. Назовите плоскость, которой принадлежит точка Р.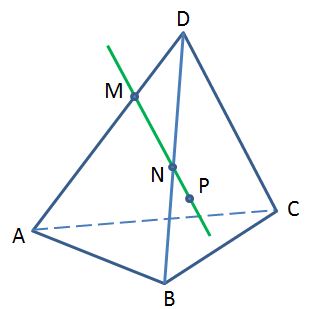
1) АВС 2) DBC 3) DAB 4) DAC
|
2
|
Каким плоскостям принадлежит точка К? 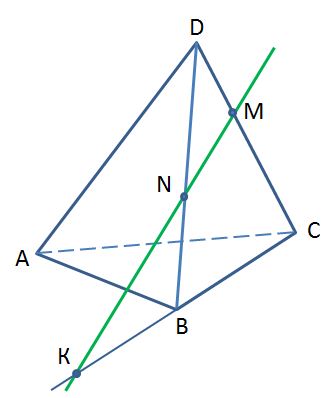
1) АВС и ABD
2) ABD и BCD
3) ACD и ABD
4) ABC и BCD
|
3
|
Выберите верные высказывания:
1) Любые три точки лежат в одной плоскости.
2) Если центр окружности и ее точка лежат в плоскости, то и вся окружность лежит в этой плоскости.
3) Через три точки, лежащих на прямой, проходит только одна плоскость.
4) Через две пересекающихся прямые проходит плоскость , и притом только одна.
Ответ: ______
|
4
|
Выберите неверные высказывания:
1) Если три прямые имеют общую точку, то они лежат в одной плоскости.
2) Прямая, пересекающая две стороны треугольника, лежит в плоскости этого треугольника.
3) Две плоскости могут имеет только две общие точки.
4) Три попарно пересекающиеся в разных точках прямые, лежат в одной плоскости.
Ответ: ______
|
5
|
Назовите прямую, по которой пересекаются плоскости A1BC и A1AD. 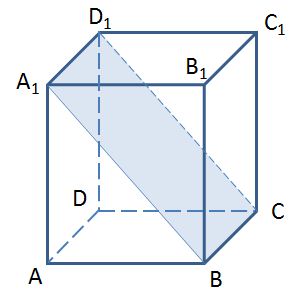
1) DC 2) A1D1
3) D1D 4) D1C
|
6
|
Назовите прямую, по которой пересекаются плоскости DCC1 и A1AD. 
1) DC 2) A1D1
3) D1D 4) D1C
|
7
|
Прямые АВ и CD пересекаются. Через прямую АВ проведена плоскость. Назовите линию пересечения данной плоскости с плоскостью ВСD.
1) АС 2) АB 3) BС 4) ВD
|
8
|
Прямые АВ и CD пересекаются. Через точки В и D проведена плоскость. Назовите линию пересечения данной плоскости с плоскостью AСD.
1) АС 2) АB 3) BС 4) ВD
|
|
|
|
|
Тест 1
Аксиомы стереометрии
Вариант 2
1
|
Точка Р лежит на прямой МN. Назовите плоскость, которой принадлежит точка Р.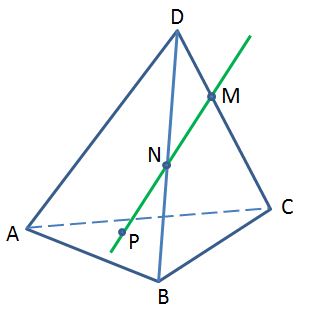
1) АВС 2) DBC 3) DAB 4) DAC
|
2
|
Каким плоскостям принадлежит точка F? 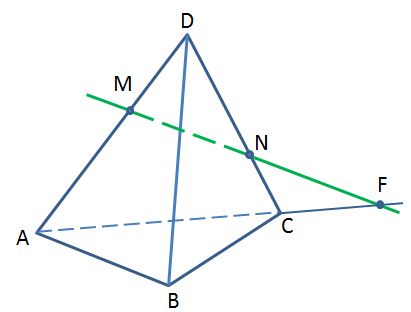
1) АВС и ACD
2) ABD и BCD
3) ACD и BCD
4) ABC и BCD
|
3
|
Выберите верные высказывания:
1) Любые четыре точки лежат в одной плоскости.
2) Через прямую и не лежащую на ней точку проходит только одна плоскость.
3) Если три точки окружности лежат в плоскости, то и вся окружность лежит в этой плоскости .
4) Две плоскости могут иметь только одну общую точку.
Ответ: ______
|
4
|
Выберите неверные высказывания:
1) Две окружности, имеющие общий центр, лежат в одной плоскости .
2) Прямая, проходящая через вершину треугольника, лежит в плоскости этого треугольника.
3) Три вершины треугольника принадлежат одной плоскости.
4) Через две параллельные прямые проходит плоскость , и притом только одна.
Ответ: ______
|
5
|
Назовите прямую, по которой пересекаются плоскости DCC1 и A1BC. 
1) DC 2) A1D1
3) D1D 4) D1C
|
6
|
Назовите прямую, по которой пересекаются плоскости ABC и C1CB. 
1) BC 2) B1C1
3) A1B 4) B1B
|
7
|
Прямые АВ и CD пересекаются. Через прямую CD проведена плоскость. Назовите линию пересечения данной плоскости с плоскостью AВС.
1) СD 2) АD 3) BС 4) ВD
|
8
|
Прямые АВ и CD пересекаются. Через точки A и D проведена плоскость. Назовите линию пересечения данной плоскости с плоскостью BСD.
1) АС 2) АD 3) BС 4) ВD
|
|
|
|
|
Тест 2
Параллельность прямых и плоскостей
Вариант 1
1
|
Точки М, Р, К – середины ребер DA, DB, DC тетраэдра DABC. Назовите прямую, параллельную плоскости FBC.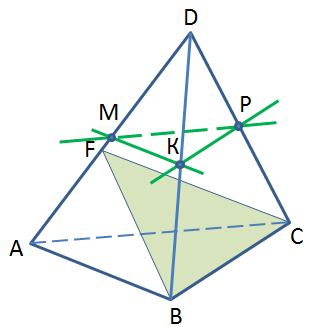
1) МР 2) РК 3) МК 4) МК и РК
|
2
|
АВСDA1B1C1D1 – прямоугольный параллелепипед. Какая из прямых параллельна плоскости A1B1C1?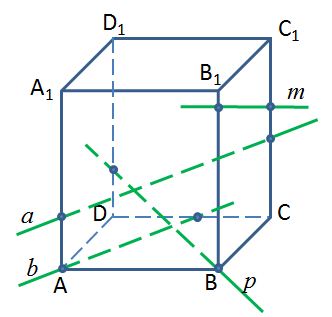
1) а 2) b 3) p 4) m
|
3
|
В тетраэдре DАВС ВК = КС, DP = PC. Плоскости какой грани параллельна прямая РК?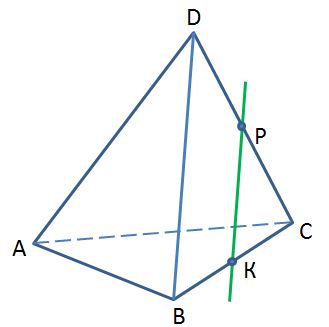
1) DAB 2) DBC 3) DAC 4) ABC
|
4
|
Выберите верные высказывания:
1) Две прямые в пространстве называются параллельными, если они не пересекаются.
2) Если одна из двух параллельных прямых параллельна плоскости, то другая прямая либо так же ей параллельна, либо лежит в этой плоскости.
3) Существует такая прямая, которая лежит в плоскости и параллельна прямой, пересекающей данную плоскость.
4) Скрещивающиеся прямые не имеют общих точек.
Ответ: ______
|
5
|
Точки А, В, С и D – середины ребер прямоугольного
параллелепипеда. Назовите параллельные прямые.
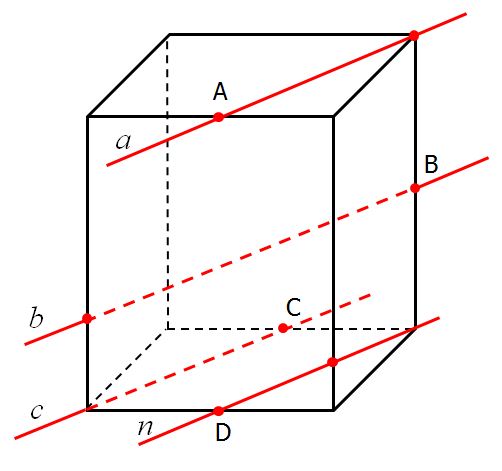
1) a || n 2) a || b
3) b || c 4) a || c
|
6
|
Точки А и D – середины ребер параллелепипеда. Выберите верные высказывания: 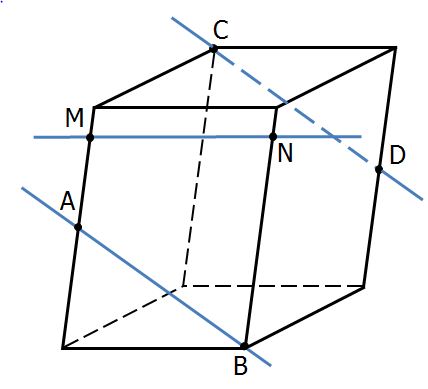
1) Прямые СD и MN скрещивающиеся.
2) Прямые АВ и MN лежат в одной плоскости.
3) Прямые СD и MN пересекаются.
4) Прямые АВ и СD скрещивающиеся.
Ответ: ______
|
7
|
Определите взаимное расположение прямых. 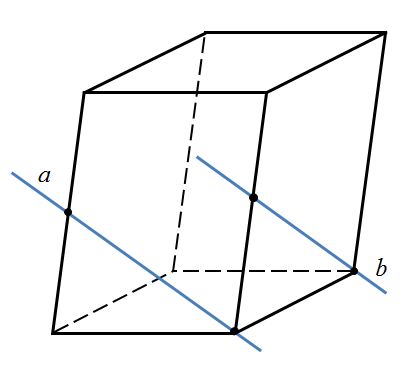
1) a и b – пересекающиеся прямые
2) a и b – параллельные прямые
3) a и b – скрещивающиеся прямые
|
8
|
Определите взаимное расположение прямых. 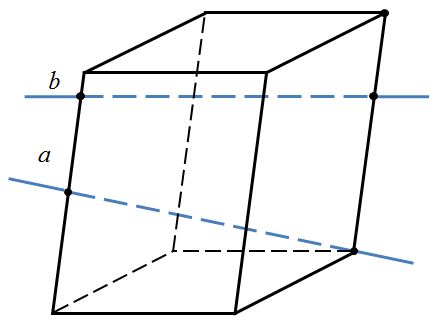
1) a и b – пересекающиеся прямые
2) a и b – параллельные прямые
3) a и b – скрещивающиеся прямые
|
9
|
Треугольники АВК и АВF расположены так, что прямые АВ и FK скрещиваются. Как расположены прямые АК и ВF?
1) они параллельны 2) скрещиваются 3) пересекаются
|
10
|
В тетраэдре DАВС АВ = ВС = АС = 20; DA = DB = DC = 40. Через середину ребра АС плоскость, параллельная АD и ВC. Найдите периметр сечения.
Ответ: ____
|
Тест 2
Параллельность прямых и плоскостей
Вариант 2
1
|
Точки М, Р, К – середины ребер DA, DB, DC тетраэдра DABC. Назовите прямую, параллельную плоскости FАB.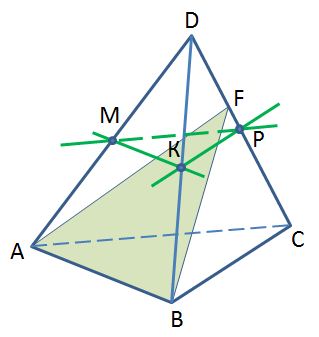
1) МР 2) РК 3) МК 4) МК и РК
|
2
|
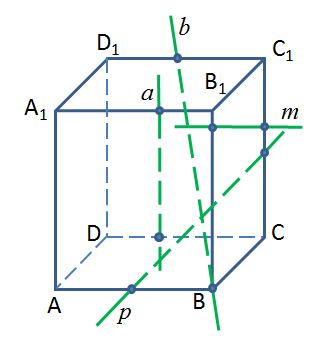
АВСDA1B1C1D1 – прямоугольный параллелепипед. Какая из прямых параллельна плоскости A1AD?
1) а 2) b 3) p 4) m
|
3
|
В тетраэдре DАВС AM = MD, AN = NB. Плоскости какой грани параллельна прямая MN?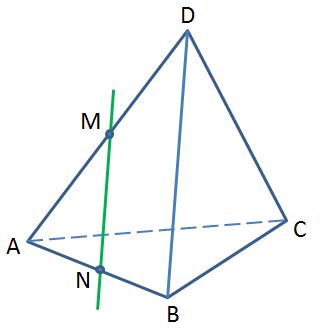
1) DAB 2) DBC 3) DAC 4) ABC
|
4
|
Выберите верные высказывания:
1) Параллельные прямые не имеют общих точек.
2) Если прямая параллельна данной плоскости, то она параллельна любой прямой, лежащей в этой плоскости.
3) Если прямая параллельна линии пересечения двух плоскостей и не принадлежит ни одной из них, то она параллельна каждой из этих плоскостей.
4) Существует параллелепипед, у которого все углы граней острые.
Ответ: ______
|
5
|
Точки А, В, С и D – середины ребер прямоугольного
параллелепипеда. Назовите параллельные прямые.
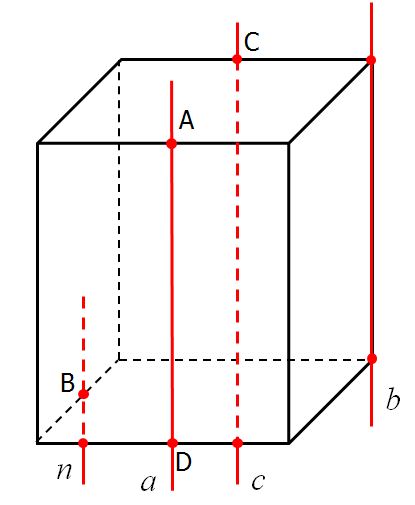
1) a || n 2) a || b
3) b || c 4) a || c
|
6
|
Точки А и D – середины ребер параллелепипеда. Выберите верные высказывания: 
1) Прямые СD и MN пересекаются.
2) Прямые АВ и MN скрещивающиеся
3) Прямые АВ и СD параллельные.
4) Прямые АВ и MN пересекаются
Ответ: ______
|
7
|
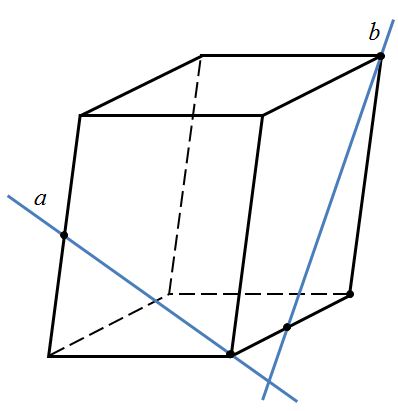
Определите взаимное расположение прямых.
1) a и b – пересекающиеся прямые
2) a и b – параллельные прямые
3) a и b – скрещивающиеся прямые
|
8
|
Точки А и В – середины ребер параллелепипеда. Определите взаимное расположение прямых. 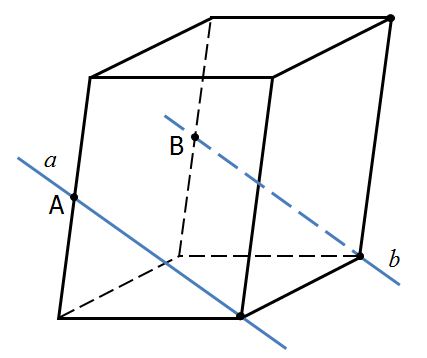
1) a и b – пересекающиеся прямые
2) a и b – параллельные прямые
3) a и b – скрещивающиеся прямые
|
9
|
Два равнобедренных треугольника АВС и АВD с общим основанием АВ расположены так, что точка С не лежит в плоскости АВD. Определите взаимное расположение прямых, содержащих медианы треугольников, проведенных к сторонам ВС и ВD.
1) они параллельны 2) скрещиваются 3) пересекаются
|
10
|
В тетраэдре DАВС АВ = ВС = АС = 10; DA = DB = DC = 20. Через середину ребра ВС плоскость, параллельная АС и ВD. Найдите периметр сечения.
Ответ: ____
|
Тест 3
Перпендикулярность прямых и плоскостей
Вариант 1
1
|
Через сторону АВ треугольника АВС проведена плоскость, перпендикулярная к стороне ВС. Определите вид треугольника относительно углов.
1) остроугольный 2) прямоугольный 3) тупоугольный
|
2
|
Треугольник АВС – правильный, О – центр треугольника. 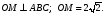 Расстояние от точки М до вершины А равно 3. Найдите высоту треугольника. Расстояние от точки М до вершины А равно 3. Найдите высоту треугольника.
Ответ: ____
|
3
|
АВСD – параллелограмм; 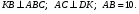 Найдите периметр параллелограмма. Найдите периметр параллелограмма.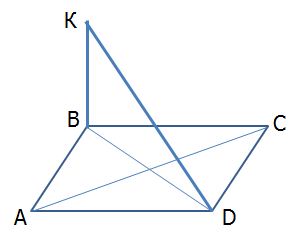
1) 20 2) 25 3) 40 4) 60
|
4
|
Через вершину А треугольника ABC проведена плос�кость α, параллельная ВС. Расстояние от ВС до плоскости α равно 12. Найдите расстояние от точки пересечения ме�диан треугольника АВС до этой плоскости.
1) 8 2) 6 3) 12 4) 18
|
5
|
Высота ромба равна 12. Точка М равноудалена от всех сторон ромба и находится на расстоянии, равном 8, от его плоскости. Чему равно расстояние точки М до сторон ромба?
Ответ: ____
|
6
|
На рисунке 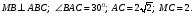 Найдите угол между МС и плоскостью АМВ. Найдите угол между МС и плоскостью АМВ. 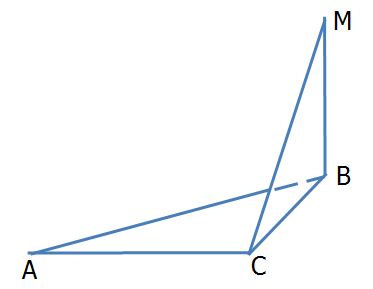
1) 300 2) 600 3) 900 4) 450
|
7
|
Выберите верные высказывания:
1) Прямая пересекает параллельные плоскости под разными углами.
2) Две прямые, перпендикулярные к одной плоскости, параллельны.
3) Длина перпендикуляра меньше длины наклонной, проведенной из той же точки.
4) Две скрещивающиеся прямые могут быть перпендикулярными к одной плоскости.
Ответ: ______
|
8
|
Отрезок АВ упирается концами А и В в грани прямого двугранного угла. Расстояния от точек А и В до ребра равны 1, а длина отрезка АВ равна 3. Найдите длину про�екции этого отрезка на ребро.
1) 2 2) 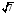 3) 3 4) 3) 3 4) 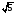
|
9
|
В тетраэдре DABC 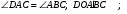 АО пресекает ВС в точке Е; АО пресекает ВС в точке Е; 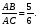 Найдите Найдите 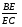 . .
1) 3 2) 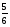 3) 3) 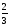 4) 4) 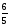
|
10
|
Прямоугольник ABCD и параллелограмм ВЕМС распо�ложены так, что их плоскости взаимно перпендикулярны. Найдите угол MCD.
1) 900 2) 600 3) 300 4) 450
|
Тест 3
Перпендикулярность прямых и плоскостей
Вариант 2
1
|
Через сторону АD параллелограмма АВСD, проведена плоскость, перпендикулярная к стороне DС. Определите вид треугольника АВС.
1) остроугольный 2) прямоугольный 3) тупоугольный
|
2
|
Треугольник АВС – правильный, О – центр треугольника. 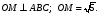 Высота треугольника равна 3. Найдите расстояние от точки М до вершин треугольника. Высота треугольника равна 3. Найдите расстояние от точки М до вершин треугольника.
Ответ: ____
|
3
|
АВСD – параллелограмм; 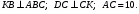 Найдите BD. Найдите BD.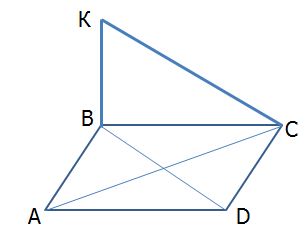
1) 20 2) 15 3) 40 4) 10
|
4
|
Через вершину А треугольника ABC проведена плос�кость α, параллельная ВС. Расстояние от точки пересече�ния медиан треугольника АВС до этой плоскости равно 4. На каком расстоянии от плоскости находится ВС?
1) 8 2) 6 3) 12 4) 14
|
5
|
Точка Р удалена от всех сторон ромба на расстояние» равное 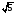 , и находится от его плоскости на расстоянии равном 2. Чему равна сторона ромба, если его угол 30°? , и находится от его плоскости на расстоянии равном 2. Чему равна сторона ромба, если его угол 30°?
Ответ: ____
|
6
|
На рисунке 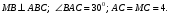 Найдите угол между МС и плоскостью АМВ. Найдите угол между МС и плоскостью АМВ. 
1) 300 2) 600 3) 900 4) 450
|
7
|
Выберите верные высказывания:
1) Угол между прямой и плоскостью может быть не больше 900.
2) Две плоскости, перпендикулярные к одной прямой, пересекаются.
3) Длина перпендикуляра больше длины наклонной, проведенной из той же точки.
4) Диагональ прямоугольного параллелепипеда больше любого из ребер.
Ответ: ______
|
8
|
Отрезок АВ упирается концами А и В в грани прямого двугранного угла. Расстояния от точек А и В до ребра равны 2, а длина отрезка АВ равна 4. Найдите длину про�екции этого отрезка на ребро.
1) 3 2) 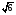 3) 3) 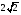 4) 4) 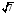
|
9
|
В тетраэдре DABC основание ABC — правильный тре�угольник. Вершина D проецируется в его центр О. Найди�те угол между плоскостью ADO и гранью DCB.
1) 300 2) 600 3) 900 4) 450
|
10
|
Треугольник АМВ и прямоугольник ABCD расположе�ны так, что их плоскости взаимно перпендикулярны. Най�дите угол MAD.
1) 900 2) 600 3) 300 4) 450
|
Тест 4
Многогранники
Вариант 1
1
|
В правильной шестиугольной призме диагонали равны 10 и 8. Найдите сторону основания призмы.
Ответ: ______
|
2
|
Основанием прямой призмы АВСА1В1С1, служит прямо�угольный треугольник ABC (угол С равен 90°); АС = 4; ВС = 3; ВВ1 = 4. Найдите площадь сечения AB1C.
1) 10 2) 8 3) 12 4) 16
|
3
|
Сторона основания правильной четырехугольной при�змы ABCDA1B1C1D1 равна 3, а боковое ребро 4. Найдите площадь сечения, которое проходит через сторону осно�вания AD и вершину С1.
1) 20 2) 18 3) 12 4) 15
|
4
|
В правильной четырехугольной пирамиде угол между противоположными боковыми гранями равен 40°. Найди�те угол наклона боковых граней к плоскости основания.
1) 600 2) 800 3) 700 4) 900
|
5
|
Основанием пирамиды MABCD служит квадрат со сто�роной, равной 6. Ребро MB перпендикулярно к плоскости основания. Равные боковые ребра равны 8. Найдите пло�щади наклонных боковых граней.
1) 20 2) 28 3) 18 4) 24
|
6
|
Основанием пирамиды DABC служит прямоугольный треугольник (угол С равен 90°). Грань ADC перпендикуляр�на к плоскости основания, а грани ADB и CDB равно на�клонены к плоскости основания; DK — высота пирамиды; АК : КС =2:1. Чему равен угол ВАС?
1) 600 2) 300 3) 450 4) 900
|
7
|
Чему равна сумма всех плоских углов четырехугольной пирамиды?
1) 9600 2) 10800 3) 7200 4) 18000
|
8
|
В правильной треугольной пирамиде высота равна стороне основания. Какой угол составляют боковые ребра с плоскостью основания?
1) 600 2) 500 3) 300 4) 400
|
9
|
В правильной четырехугольной усеченной пирамиде стороны оснований 8 м и 2 м. Высота равна 4 м. Найдите площадь полной поверхности (в м2).
Ответ: ______
|
10
|
Стороны оснований усеченной правильной треугольной пирамиды равны 2 см и 6 см. Боковая грань образует с большим основанием угол 600. Найдите высоту (в см).
Ответ: ______
|
Тест 4
Многогранники
Вариант 2
1
|
В правильной шестиугольной призме сторона основа�ния равна 7, а меньшая диагональ — 24. Найдите длину большей диагонали призмы.
Ответ: ______
|
2
|
В наклонной треугольной призме боковое ребро равно 10, площади двух боковых граней равны 30 и 40, угол между ними прямой. Найдите площадь боковой поверх�ности призмы.
1) 100 2) 120 3) 110 4) 150
|
3
|
Сторона основания правильной четырехугольной при�змы ABCDA1B1C1D1 равна 4, а боковое ребро 5. Найдите площадь сечения, которая проходит через ребро АА1 и вершину С.
1) 32 2) 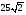 3) 36 4) 3) 36 4) 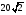
|
4
|
В правильной четырехугольной пирамиде боковые грани наклонены к основанию под углом 50°. Найдите угол между противоположными боковыми гранями.
1) 600 2) 800 3) 700 4) 900
|
5
|
Основанием пирамиды DABC служит прямоугольный треугольник (угол С равен 90°); угол А равен 30°. Грань ADC перпенди�кулярна к плоскости основания, а грани ADB и CDB накло�нены к основанию под углом 60°; АС = 3. Найдите высоту пирамиды.
1) 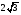 2) 2) 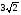 3) 3) 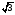 4) 4) 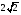
|
6
|
Основанием пирамиды служит трапеция, основания которой равны 2 и 8. Боковые грани пирамиды равно на�клонены к плоскости основания. Высота одной из боко�вых граней равна 10. Найдите площадь боковой поверх�ности пирамиды.
1) 100 2) 120 3) 80 4) 116
|
7
|
Чему равна сумма всех плоских углов треугольной пирамиды?
1) 9600 2) 5400 3) 7200 4) 3600
|
8
|
Высота правильной шестиугольной пирамиды вдвое меньше стороны основания. Какой угол составляют бо�ковые грани с плоскостью основания?
1) 600 2) 500 3) 300 4) 400
|
9
|
В правильной четырехугольной усеченной пирамиде высота равна 2, а стороны оснований 3 и 5. Найдите диагональ этой пирамиды
Ответ: ______
|
10
|
В правильной треугольной усеченной пирамиде сторона нижнего основания равна 8, верхнего – 5, а высота – 3. Найдите площадь сечения, проведенного через сторону нижнего основания и противоположную вершину верхнего основания.
Ответ: ______
|
Тест 5
Векторы в пространстве
Вариант 1
1
|
ABCDA1B1C1D1 - параллелепипед. Укажите вектор, равный сумме
→ → → →
AB + B1C1 + DD1 + CD.
→ → → →
AD1 2) AD 3) B1D1 4) AB1
|
2
|
Ребро куба ABCDA1B1C1D1 равно 1.
→ →
Найдите │DC1 – DA1│
1) 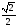 2) 2) 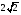 3) 2 4) 3) 2 4) 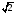
|
3
|
ABCDA1B1C1D1 – параллелепипед. A1С пересекает В1D в точке М.
→ →
A1C = x . CM. Найдите x.
1) 3 2) -2 3) -1 4) 2
|
4
|
Выберите верные высказывания:
1) Векторы, имеющие равные длины, равны.
2) Векторы, лежащие на двух прямых, перпендикулярных к одной плоскости, коллинеарны.
3) Любые два вектора компланарны.
4) Векторы коллинеарны, если они лежат в двух параллельных плоскостях..
Ответ: ______
|
5
|
→ →
В тетраэдре DABC назовите вектор, равный сумме BC + CD.
→ → → →
DB 2) BD 3) DC 4) CD
|
|
6
|
Диагонали куба ABCDA1B1C1D1 пересекаются в точке О.
→ →
Найдите число λ из равенства DB1 = λ . OB1.
Ответ: ______
|
7
|
SO – высота правильной четырехугольной пирамиды SABCD.
→ → →
Найдите число λ из равенства SA – SO = λ . AC.
Ответ: ______
|
8
|
В кубе ABCDA1B1C1D1 назовите вектор, равный сумме
→ → →
AD + A1B1 + CC1.
→ → → →
AC1 2) AC1 3) B1C1 4) DC1
|
9
|
Дан тетраэдр DABC. Назовите ребро тетраэдра, изображающее вектор , если
→ → →
векторы DA, AC, x компланарны, но никакие два из них не коллинеарны.
1) AC 2) DC 3) DA 4) AB
|
10
|
РАВСD – пирамида; АВСD – параллелограмм;
|
→ → → → → → → → → → →
PA = a, PB = b, PC = c. Выразите вектор PD = x через векторы a, b, c.
→ → → → → → → → → → → → → → → →
x = a + b + c 2) x = a - b + c 3) x = a – b - c 4) x = a + b – c.
Тест 5
Векторы в пространстве
Вариант 2
1
|
ABCDA1B1C1D1 - параллелепипед. Укажите вектор, равный сумме
→ → → →
BC + C1D1 + A1A + DB1
→ → → →
BD1 2) BB1 3) 0 4) CD1
|
2
|
В правильной треугольной призме ABCA1B1C1 сторона основания равна 1, точка Е – середина А1С1.
→ →
Найдите │CE – CB1│
1) 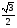 2) 2) 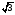 3) 3) 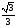 4) 4) 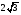
|
3
|
ABCDA1B1C1D1 – параллелепипед. A1С пересекает В1D в точке М.
→ →
B1D = x . DM. Найдите x.
1) 3 2) -2 3) -1 4) 2
|
4
|
Выберите верные высказывания:
1) Длины равных векторов равны.
2) Векторы, лежащие на двух прямых, параллельных одной плоскости, коллинеарны.
3) Любые три вектора некомпланарны.
4) Векторы, лежащие на боковых ребрах призмы, коллинеарны.
Ответ: ______
|
5
|
→ →
В тетраэдре DABC назовите вектор, равный сумме DA + AB.
→ → → →
DB 2) BD 3) DC 4) CD
|
6
|
Диагонали куба ABCDA1B1C1D1 пересекаются в точке О.
→ →
Найдите число λ из равенства AO = λ . AC1.
Ответ: ______
|
7
|
SO – высота правильной четырехугольной пирамиды SABCD.
→ → →
Найдите число λ из равенства SB – SD = λ . OD.
Ответ: ______
|
8
|
В кубе ABCDA1B1C1D1 назовите вектор, равный сумме
→ → →
AB + A1D1 + CC1.
→ → → →
AC1 2) A1C 3) D1C1 4) DC1
|
9
|
Дан тетраэдр DABC. Назовите ребро тетраэдра, изображающее вектор x, если
→ → →
векторы DA, AC и х компланарны, но никакие два из них не коллинеарны.
1) AC 2) DC 3) DA 4) AB
|
10
|
В пирамиде PАВСD основанием служит параллелограмм АВСD;
|
→ → → → → → → → → → → →
PB = m, PC = n, PD = p, PA = y. Выразите вектор y через векторы m, n, p.
→ → → → → → → → → → → → → → → →
y = m + n + p 2) y = m + n - p 3) y = m – n + p 4) y = m – n – p.
Ответы
Тест 1
№
|
1
|
2
|
3
|
4
|
5
|
6
|
7
|
8
|
9
|
10
|
Вариант 1
|
3
|
4
|
14
|
13
|
2
|
3
|
2
|
4
|
|
|
Вариант 2
|
2
|
1
|
23
|
12
|
4
|
1
|
1
|
2
|
|
|
Тест 2
№
|
1
|
2
|
3
|
4
|
5
|
6
|
7
|
8
|
9
|
10
|
Вариант 1
|
2
|
2
|
1
|
24
|
4
|
12
|
3
|
1
|
2
|
60
|
Вариант 2
|
3
|
4
|
2
|
13
|
2
|
34
|
3
|
2
|
3
|
30
|
Тест 3
№
|
1
|
2
|
3
|
4
|
5
|
6
|
7
|
8
|
9
|
10
|
Вариант 1
|
2
|
1,5
|
3
|
1
|
10
|
4
|
23
|
2
|
2
|
1
|
Вариант 2
|
2
|
3
|
4
|
2
|
4
|
1
|
14
|
3
|
3
|
1
|
Тест 4
№
|
1
|
2
|
3
|
4
|
5
|
6
|
7
|
8
|
9
|
10
|
Вариант 1
|
6
|
1
|
4
|
3
|
4
|
2
|
2
|
1
|
168
|
2
|
Вариант 2
|
25
|
2
|
4
|
2
|
3
|
1
|
3
|
3
|
6
|
24
|
Тест 5
№
|
1
|
2
|
3
|
4
|
5
|
6
|
7
|
8
|
9
|
10
|
Вариант 1
|
1
|
4
|
2
|
23
|
2
|
2
|
-0,5
|
2
|
4
|
2
|
Вариант 2
|
3
|
1
|
2
|
14
|
1
|
0,5
|
-2
|
1
|
2
|
3
| |
|
|
 Скачать 278.38 Kb.
Скачать 278.38 Kb.

















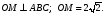 Расстояние от точки М до вершины А равно 3. Найдите высоту треугольника.
Расстояние от точки М до вершины А равно 3. Найдите высоту треугольника.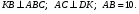 Найдите периметр параллелограмма.
Найдите периметр параллелограмма.
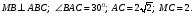 Найдите угол между МС и плоскостью АМВ.
Найдите угол между МС и плоскостью АМВ. 
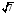 3) 3 4)
3) 3 4) 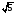
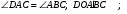 АО пресекает ВС в точке Е;
АО пресекает ВС в точке Е; 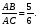 Найдите
Найдите 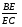 .
.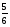 3)
3) 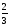 4)
4) 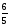
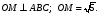 Высота треугольника равна 3. Найдите расстояние от точки М до вершин треугольника.
Высота треугольника равна 3. Найдите расстояние от точки М до вершин треугольника.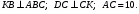 Найдите BD.
Найдите BD.
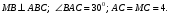 Найдите угол между МС и плоскостью АМВ.
Найдите угол между МС и плоскостью АМВ. 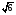 3)
3) 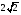 4)
4) 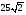 3) 36 4)
3) 36 4) 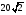
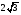 2)
2) 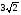 3)
3) 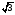 4)
4) 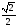 2)
2) 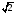
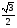 2)
2) 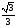 4)
4)