Учебник Макарычев. 2007 г. Тема урока «Квадратный корень из произведения»

Скачать 37.02 Kb. Название Учебник Макарычев. 2007 г. Тема урока «Квадратный корень из произведения» Дата 12.02.2016 Размер 37.02 Kb. Тип Учебник

1. /Тема урокаквадратный корень из произведения.doc Учебник Макарычев. 2007 г. Тема урока «Квадратный корень из произведения» Алгебра 8 учебник Макарычев. 2007 г. Тема урока « Квадратный корень из произведения» Цели урока: изучить правило вычисления квадратного корня из произведения, ввести свойство с помощью проблемной ситуации, формировать умение применять свойство к решению примеров в стандартной и нестандартной ситуациях; развивать вычислительные навыки, умение анализировать, сравнивать и делать выводы; воспитывать умение работать в группе, оказывать взаимопомощь. Оборудование: задания с практической работой, задания на больших плакатных листах, презентация к уроку, сигнальные карточки. Ход урока. Оргмомент. Актуализация знаний ( 4-5 мин) Вычислите устно: ( с сигнальными карточками) 3. Постановка учебной задачи.(4-5мин). Смогли ли вы выполнить последнее задание? В чем затруднение? Какой вопрос возникает? Сможем ли мы ответить на него с помощью определения квадратного корня? ( Нет) Как обычно мы поступаем, если нам мало определения? ( Ищем свойства и пользуемся ими). Чем будем заниматься сегодня на уроке? Какова тема урока? Свойства арифметического квадратного корня. Квадратный корень из произведения. Сформулируйте возникшую перед нами проблему? Итак, мы будем учиться умножать арифметические квадратные корни значения, которых мы не можем найти. Как вы думаете, как можно решить эту проблему? ( Учитель слушает гипотезы детей). Попробуем проверить ваши гипотезы, подтвердить или опровергнуть их в ходе выполнения практической работы. Практическая работа по группам ( 5-7 минут). 1 группа (Хандогина А, Новикова В., Мищенкова Ю, МИщенкова Н.) 2 группа ( Черепанова Ф., Кривенкова М, Серченкова Т.) Задания раздаются на больших листах, записаны маркерами, ученики решают их устно и записывают ответы на листах тоже маркерами. Результаты работы вывешиваются на доску с помощью магнитов. Задание 1 группе. Решите примеры. Сравните примеры а) и б), в) и г) и сделайте вывод. Продолжите утверждение: Корень из произведения_________________________________________________________________________________________________________________. 5. Обсуждение результатов работы групп ( 1-2 мин). 1) Вывесить на доску 2) Какой вывод сделали? ( Заслушиваем выводы групп по очереди). Сверим ваши утверждения с формулировкой свойства арифметического квадратного корня в учебнике с.80. О чем вы не сказали? Важно ли помнить об этих ограничениях? Да, так как речь идет об арифметическом квадратном корне. (Записываем формулировку в тетрадь по правилам.) 6. Рассмотрим теперь, строгое доказательство этого свойства. ( По слайду). Корень из произведения неотрицательных множителей, равен произведению корней из этих множителей. 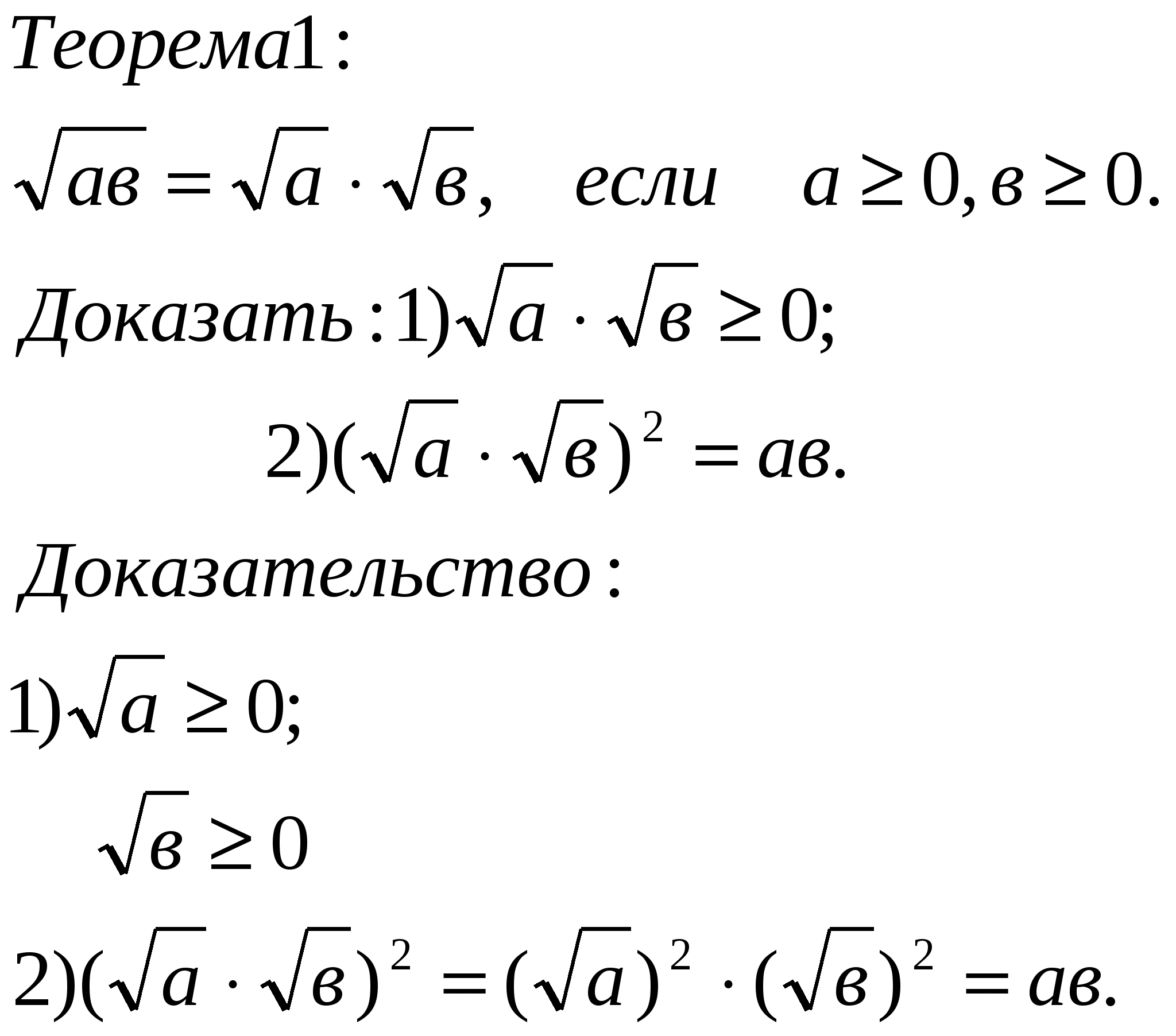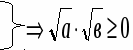▄ Вопросы на усвоение теоремы: Как звучит формулировка теоремы? Каковы этапы доказательства теоремы? Как можно на основе этой теоремы сформулировать правило извлечения квадратного корня из произведения? Будет ли теорема верна, если произведение будет содержать три множителя? А больше? Верно. - тождество, и значит им можно пользоваться как слева, так и справа. Попробуем им воспользоваться для решения примера, вызвавшего у нас затруднение. 7. Первичное закрепление. №357( в, д), № 360(а, в) – у доски с проговариванием свойства корня. 8. Закрепление. Работа по группам. О – группа Работа по обучающим карточкам. Остальные 1 и2 – группы.№362( I стр) ( Трудность. Как решить? Выражение под знаком корня разложить на такие множители, чтобы из них извлекались квадратные корни. Количество множителей не ограничено.) № 372(Iстр) ( Под один корень и разложить на множители) № 364(а, в,б) Прием разложения на множители по формуле разности квадратов. В примере б – по действиям. 9. Самопроверка, саморефлексия. Найдите значение выражения: Самопроверка и самооценка по решению на слайде ( оценка «+» или «-»каждого задания). 10. Итог урока. С какой теоремой мы сегодня познакомились? Как формулируется правило извлечения квадратного корня из произведения? Когда пользуемся этим правилом? Как поступаем, если числа, стоящие под корнем, не являются квадратами? Как поступаем, если число дробное? 11. Домашнее задание 0 группа на «3».конспект учить формулировку. №№ 372(а,б,г,ж), 359 (а,б). 2 группа на «4» №№361(а,б), 365( а-г), 374(а-в). На»5» + доказательство теоремы. Обучающая карточка по теме «Квадратный корень из произведения». Рассмотри образец и запиши его себе в тетрадь. Образец: Выполните по образцу: Образец: Выполните по образцу: Реши № 360(а,б). Обучающая карточка по теме «Квадратный корень из произведения». Рассмотри образец и запиши его себе в тетрадь. Образец: Выполните по образцу: Образец: Выполните по образцу: Реши № 360(а,б). Обучающая карточка по теме «Квадратный корень из произведения». Рассмотри образец и запиши его себе в тетрадь. Образец: Выполните по образцу: Образец: Выполните по образцу: Реши № 360(а,б).