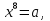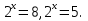|
Программа по алгебре и началам анализа для 10 класса (физико-математический профиль)
Рабочая учебная программа по алгебре и началам анализа
для 10 класса (физико-математический профиль)
Разработана на основе авторской программы по алгебре и началам анализа
А.Г. Мордковича.
Пояснительная записка.
Данная рабочая программа ориентирована на учащихся 10 классов физико –математического профиля и реализуется на основе следующих документов:
1. 1. Программы. Математика 5-6 классы. Алгебра 7-9 классы. Алгебра и начала анализа 10-11 классы /авторы-составители И.И. Зубарева, А.Г. Мордкович. – М. Мнемозина, 2008г. – 64с.
2. Государственный стандарт образования по математике.
Программа соответствует учебному комплекту
«Алгебра и начала анализа. Профильный уровень. Часть 1 Учебник 10 класс» и «Алгебра и начала анализа. Профильный уровень. Часть 2 Задачник 10 класс» для общеобразовательных учреждений / А.Г. Мордкович и др. – М. Мнемозина, 2007 г.
Выбор данного учебника обусловлен преемственностью линии УМК под ред. А.Г. Мордковича и соавторов.
Преподавание ведется по варианту – 4 часа в неделю, всего 140 часов, тема «Комбинаторика и вероятность « перенесена для изучения в 11 класс.
Главной целью образования является развитие ребёнка как компетентной личности путём включения его в различные виды ценностной человеческой деятельности. Обучение рассматривается как процесс овладения не только определенной суммой знаний и системой соответствующих умений и навыков, но и как процесс овладения компетенциями.
Цели обучения алгебре и началам анализа:
овладение системой математических знаний и умений, необходимых для применения в практической деятельности, изучения смежных дисциплин, продолжения образования;
интеллектуальное развитие, формирование качеств личности, необходимых человеку для полноценной жизни в современном обществе: ясность и точность мысли, критичность мышления, интуиция, логическое мышление, элементы алгоритмической культуры, пространственных представлений, способность к преодолению трудностей;
формирование представлений об идеях и методах математики как универсального языка науки и техники, средства моделирования явлений и процессов;
воспитание культуры личности, отношения к математике как к части общечеловеческой культуры, понимание значимости математики для научно-технического прогресса.
На основании требований Государственного образовательного стандарта 2004г. В содержании календарно-тематического планирования предполагается реализовать компетентностный, деятельностный подходы, которые определяют задачи обучения:
приобретение математических знаний и умений;
овладение обобщёнными способами мыслительной творческой деятельностей;
освоение компетенций: учебно-познавательной, коммуникативной, рефлексивной, личностного саморазвития, ценностно-ориентационной и профессионально-трудового выбора.
При изучении алгебры и начал анализа в старшей школе осуществляется переход от методики поурочного планирования к блочно-модульной системе организации учебного процесса. Тематическое планирование составлено с учетом применения при обучении алгебре и началам анализа блочно-модульной технологии. Каждый тематический блок состоит из нескольких модулей: ПМ - проблемный модуль, ИМ - информационный модуль, РМ - расширенный модуль, МС - модуль систематизации, МКЗ - модуль коррекции знаний.
Модуль
|
Содержание модуля
|
Проблемный
|
Создание проблемной ситуации, приводящей к появлению нового понятия.
|
Информационный
|
Изучение нового материала единым блоком, разработка алгоритмов решения задач и классификация их основных типов.
|
Расширенный
|
Углубление и расширение теоретического материала. Решение более сложных, нестандартных задач
|
Систематизации
|
Обобщение и систематизация материала блока
|
Коррекции знаний
|
Ликвидация пробелов
|
Контроля
|
Учёт знаний учащихся:
а) текущий контроль;
б) контроль выполнения домашних заданий;
в) итоговый контроль.
|
Содержание программы
Числовые функции (17ч)
Определение числовой функции и способы её задания. Свойства функций. Периодические и обратные функции.
Тригонометрические функции (24ч)
Числовая окружность. Определение синуса, косинуса, тангенса и котангенса. Тригонометрические функции, их свойства и графики. Преобразование графиков. Обратные тригонометрические функции.
Преобразование тригонометрических выражений. Тригонометрические уравнения и неравенства (40ч)
Тригонометрические формулы. Простейшие тригонометрические уравнения и неравенства.
Методы решения тригонометрических уравнений: метод замены переменной, метод разложения на множители, однородные тригонометрические уравнения. Простейшие тригонометрические неравенства.
Производная (18ч)
Определение числовой последовательности, способы её задания и свойства. Предел числовой последовательности, свойства сходящихся последовательностей. Сумма бесконечной геометрической прогрессии. Предел функции на бесконечности и в точке.
Задачи, приводящие к понятию производной, вычисление производных. Понятие производной n-го порядка. Дифференцирование сложной функции. Дифференцирование обратной функции.
Применение производной (23ч)
Уравнение касательной к графику функции. Применение производной для исследования функции на монотонность и экстремумы. Применение производной для доказательства тождеств и неравенств. Построение графиков функций. Применение производной для отыскания наибольшего и наименьшего значений непрерывной функции на промежутке. Задачи на оптимизацию.
Действительные и комплексные числа (14ч)
Натуральные и целые числа. Делимость чисел. Основная теорема арифметики натуральных
чисел. Рациональные, иррациональные, действительные числа, числовая прямая. Числовые неравенства. Аксиоматика действительных чисел. Модуль действительного числа. Метод математической индукции.
Комплексные числа и арифметические действия над ними. Комплексные числа и координатная плоскость. Тригонометрическая форма записи комплексного числа. Комплексные числа и квадратные уравнения. Возведение комплексного числа в степень. Извлечение квадратного и кубического корня из комплексного числа.
Требования к уровню подготовки учащихся 10 – 11 классов
(профильный уровень)
В результате изучения математики на профильном уровне ученик должен:
знать
значение математической науки для решения задач, возникающих в теории и практике; широту и ограниченность применения математических методов к анализу и исследованию процессов и явлений в природе и обществе;
значение практики и вопросов, возникающих в самой математике, для формирования и развития математической науки;
идеи расширения числовых множеств как способа построения нового математического аппарата для решения практических задач и внутренних задач математики;
значение идей, методов и результатов алгебры и математического анализа для построения моделей реальных процессов и ситуаций;
возможности геометрии для описания свойств реальных предметов и их взаимного расположения;
универсальны характер законов логики математических рассуждений, их применимости в различных областях человеческой деятельности;
различие требований, предъявляемых к доказательствам в математике, естественных, социально-экономических и гуманитарных науках, на практике;
роль аксиоматики в математике; возможность построения математических теорий на аксиоматической основе; значение аксиоматики для других областей знания и для практики;
вероятностный характер различных процессов и закономерностей окружающего мира.
Числовые и буквенные выражения
уметь
выполнять арифметические действия, сочетая устные и письменные приёмы, применение вычислительных устройств; находить значения корня натуральной степени, степени с рациональным показателем, логарифма, пользоваться оценкой и прикидкой при практических расчетах;
применять понятия, связанные с делимостью целых чисел при решении математических задач;
находить корни многочленов с одной переменной, раскладывать многочлены на множители;
выполнять действия с комплексными числами, пользоваться геометрической интерпретацией комплексных чисел, в простейших случаях находить комплексные корни уравнений с действительными коэффициентами;
проводить преобразования числовых и буквенных выражений, включающих степени, радикалы, логарифмы и тригонометрические функции;
использовать приобретенные знания и умения в практической деятельности и повседневной жизни для практических расчётов по формулам, включая формулы, содержащие степени, радикалы, логарифмы и тригонометрические функции, используя при необходимости справочные материалы и простейшие вычислительные устройства.
Функции и графики
уметь
определять значение функции по значению аргумента при различных способах задагия функции;
строить графики изученных функций, выполнять преобразования графиков;
описывать по графику и по формуле поведение и свойства функций;
решать уравнения, системы уравнений неравенства, используя свойства функций и их графические представления;
использовать приобретенные знания и умения в практической деятельности и повседневной жизни для описания и исследования с помощью функций реальных зависимостей, представления их графически; интерпретации графиков реальных процессов.
Начала математического анализа
уметь
находить сумму бесконечно убывающей геометрической прогрессии;
вычислять производные и первообразные элементарных функций, применяя правила вычисления производных и первообразных;
исследовать функции и строить их графики с помощью производной;
решать задачи с применением уравнения касательной к графику функции;
решать задачи на нахождение наибольшего и наименьшего значения функции на отрезке;
вычислять площадь криволинейной трапеции;
использовать приобретенные знания и умения в практической деятельности и повседневной жизни для решения геометрических, физических, экономических и других прикладных задач, в том числе задач на наибольшие и наименьшие значения с применением аппарата математического анализа.
Уравнения и неравенства
уметь
решать рациональные, показательные и логарифмические уравнения и неравенства, иррациональные и тригонометрические уравнения, их системы;
доказывать несложные неравенства;
решать текстовые задачи с помощью составления уравнений, и неравенств, интерпретируя результат с учётом ограничения условия задачи;
изображать на координатной плоскости множества решений уравнений и неравенств с двумя переменными и их систем;
находить приближенные решения уравнений и их систем, используя графический метод;
решать уравнения, неравенства и системы с применением графических представлений, свойств функций, производной;
использовать приобретенные знания и умения в практической деятельности и повседневной жизни для построения и исследования простейших математических моделей.
Элементы комбинаторики, статистики и теории вероятностей
уметь
решать простейшие комбинаторные задачи методом перебора, а также с использованием известных формул, треугольника Паскаля; вычислять коэффициенты бинома Ньютона по формуле и с использованием треугольника Паскаля;
вычислять вероятности событий на основе подсчета числа исходов;
использовать приобретенные знания и умения в практической деятельности и повседневной жизни для анализа реальных числовых данных, представленных в виде диаграмм , графиков; для анализа информации статистического характера.
владеть компетенциями:
учебно-познавательной; ценностно-ориентированной; рефлексивной; коммуникативной; информационной; социально-трудовой.
Тематическое планирование
Модуль
|
Тема
|
Число уроков
|
|
Блок №1 «Числовые функции»
|
17
|
ПМ
|
Что мы знаем о функциях?
|
1
|
ИМ
|
Числовая функция и способы её задания.
|
1
|
|
Преобразование графиков функций.
|
2
|
|
Свойства функций (область определения, множество значений, четность и нечетность, монотонность, ограниченность, экстремумы, наибольшее и наименьшее значения, непрерывность).
|
2
|
|
Периодичность функций.
|
1
|
|
Обратная функция.
|
1
|
РМ
|
Исследование функции.
|
3
|
|
Построение графиков.
|
2
|
МС
|
Обобщающий урок по теме
|
1
|
МКЗ
|
Урок – консультация
|
1
|
МК
|
Зачёт по теме «Числовые функции».
|
1
|
|
Контрольная работа № 1 «Числовые функции»
|
1
|
|
Блок №2
«Тригонометрические функции»
|
24
|
ПМ
|
Являются ли синус, косинус, тангенс и котангенс числовыми функциями?
|
1
|
ИМ
|
Числовая окружность.
|
2
|
|
Синус, косинус, тангенс, котангенс любого угла.
|
1
|
|
Радианная мера угла.
|
1
|
|
Функции синус, косинус, тангенс, котангенс, их свойства и график.
|
2
|
|
Определение arksin, arkkos, arktg, arkctg.
|
2
|
РМ
|
Вычисление значений тригонометрических функций.
|
3
|
|
Построение графиков функций.
|
3
|
|
График гармонического колебания.
|
1
|
|
Обратные тригонометрические функции.
|
3
|
МС
|
Защита мини – проектов.
|
1
|
МКЗ
|
Урок – консультация.
|
1
|
МК
|
Зачёт по теме «Тригонометрические функции»
|
1
|
|
Контрольная работа №2
«Тригонометрические функции»
|
2
|
|
Блок №3
«Тригонометрические выражения, уравнения и неравенства».
|
40
|
ИМ
|
Тригонометрические формулы.
|
5
|
|
Простейшие тригонометрические уравнения и неравенства.
|
3
|
|
Методы решения тригонометрических уравнений.
|
4
|
РМ
|
Преобразование тригонометрических выражений.
|
6
|
|
Решение тригонометрических уравнений.
|
6
|
|
Решение систем тригонометрических уравнений.
|
4
|
|
Решение тригонометрических неравенств.
|
4
|
МС
|
Семинар.
|
2
|
МКЗ
|
Урок – консультация(работа в группах).
|
1
|
МК
|
Зачёт по теме «Тригонометрические выражения, уравнения и неравенства»
|
1
|
|
Контрольная работа № 3 «Преобразование тригонометрических выражений».
|
2
|
|
Контрольная работа № 4 «Тригонометрические уравнения и неравенства».
|
2
|
|
Блок №4
«Производная».
|
18
|
ИМ
|
Числовые последовательности, предел последовательности и предел функции. Вычисление пределов.
|
3
|
|
Приращение аргумента и приращение функции.
|
1
|
|
Определение производной, её геометрический и механический смысл.
|
3
|
|
Формулы и правила дифференцирования.
|
3
|
РМ
|
Вычисление производных.
|
4
|
МС
|
Обобщающий урок (представление составленных контрольных работ по теме «Вычисление производных»).
|
1
|
МКЗ
|
Урок – консультация.
|
1
|
МК
|
Релейная контрольная работа по д/з.
|
1
|
|
Контрольная работа № 5 « Производная».
|
2
|
|
Блок №5
«Применение производной».
|
23
|
ПМ
|
Производная в геометрии, физике, экономике.
|
1
|
ИМ
|
Касательная к графику функции.
|
2
|
|
Исследование функции на монотонность и экстремумы.
|
1
|
|
Асимптоты графика функции.
|
1
|
|
Вторая производная, точки перегиба, выпуклость, вогнутость.
|
2
|
|
Наибольшее и наименьшее значения функции.
|
2
|
РМ
|
Задачи на касательную.
|
3
|
|
Построение графиков функций.
|
3
|
|
Производная в физике и технике.
|
2
|
|
Экстремальные задачи.
|
3
|
МК
|
Зачёт по теме «Применение производной»
|
1
|
|
Контрольная работа № 6
«Касательная к графику функций».
|
1
|
|
Контрольная работа № 7 «Применение производной для исследования функции».
|
1
|
|
Блок №6
«Действительные и комплексные числа».
|
14
|
ИМ
|
Натуральные, целые, рациональные, иррациональные, действительные числа.
|
2
|
|
Модуль действительного числа.
|
2
|
|
Метод математической индукции.
|
2
|
|
Комплексные числа и арифметические операции над ними.
|
2
|
|
Тригонометрическая форма записи комплексного числа.
|
2
|
|
Комплексные числа и квадратные уравнения. Возведение в степень, извлечение корня.
|
3
|
|
Контрольная работа № 8
«Действительные и комплексные числа».
|
1
|
|
Повторение.
|
4
|
|
ИТОГО
|
140
|
Осуществление представленной рабочей программы предполагает использование следующего учебно-методического комплекта:
А.Г. Мордкович, П.В. Семенов Алгебра и начала анализа 10 класс. Учебник для общеобразовательных учреждений (профильный уровень)– М. Мнемозина, 2007.
А.Г. Мордкович, Л.О. Денищева и др. Алгебра и начала анализа 10 класс. Задачник для общеобразовательных учреждений (профильный уровень) под редакцией А.Г. Мордковича – М. Мнемозина, 2007.
В.И. Глизбург. Алгебра и начала анализа. Контрольные работы для10 класса общеобразовательных учреждений (профильный уровень). Под редакцией А.Г. Мордковича. – М. Мнемозина, 2007.
Л.О. Денищева, Т.А. Корешкова. Алгебра и начала анализа 10-11 классы. Тематические тесты и зачёты для общеобразовательных учреждений. Под редакцией А.Г. Мордковича. – М. Мнемозина, 2006.
А.П. Ершова. В.В. Голобородько. Самостоятельные и контрольные работы по алгебре и началам анализа для 10-11 класса. Разноуровневые дидактические материалы– М. Илекса, 2007
Рабочая учебная программа по алгебре и началам анализа
для 11 класса (физико-математический профиль)
Разработана на основе авторской программы по алгебре и началам анализа
А.Г. Мордковича.
Пояснительная записка.
Данная рабочая программа ориентирована на учащихся 11 классов физико – математического профиля и реализуется на основе следующих документов:
1. 1. Программы. Математика 5-6 классы. Алгебра 7-9 классы. Алгебра и начала анализа 10-11 классы /авторы-составители И.И. Зубарева, А.Г. Мордкович. – М. Мнемозина, 2008г. – 64с.
2. Государственный стандарт образования по математике.
Программа соответствует учебному комплекту
«Алгебра и начала анализа. Профильный уровень. Часть 1 Учебник 11 класс» и «Алгебра и начала анализа. Профильный уровень. Часть 2 Задачник 11 класс» для общеобразовательных учреждений / А.Г. Мордкович и др. – М. Мнемозина, 2007 г.
В связи с переходом на БУП 2004 года, предусматривающего профильное обучение, был выбран данный учебник.
Преподавание ведется по варианту – 6 часов в неделю, всего 204 часа, на итоговое повторение отводится 67 часов.
Главной целью образования является развитие ребёнка как компетентной личности путём включения его в различные виды ценностной человеческой деятельности. Обучение рассматривается как процесс овладения не только определенной суммой знаний и системой соответствующих умений и навыков, но и как процесс овладения компетенциями.
Цели обучения алгебре и началам анализа:
овладение системой математических знаний и умений, необходимых для применения в практической деятельности, изучения смежных дисциплин, продолжения образования;
интеллектуальное развитие, формирование качеств личности, необходимых человеку для полноценной жизни в современном обществе: ясность и точность мысли, критичность мышления, интуиция, логическое мышление, элементы алгоритмической культуры, пространственных представлений, способность к преодолению трудностей;
формирование представлений об идеях и методах математики как универсального языка науки и техники, средства моделирования явлений и процессов;
воспитание культуры личности, отношения к математике как к части общечеловеческой культуры, понимание значимости математики для научно-технического прогресса.
На основании требований Государственного образовательного стандарта 2004г. В содержании календарно-тематического планирования предполагается реализовать компетентностный, деятельностный подходы, которые определяют задачи обучения:
приобретение математических знаний и умений;
овладение обобщёнными способами мыслительной творческой деятельностей;
освоение компетенций: учебно-познавательной, коммуникативной, рефлексивной, личностного саморазвития, ценностно-ориентационной и профессионально-трудового выбора.
При изучении алгебры и начал анализа в старшей школе осуществляется переход от методики поурочного планирования к блочно-модульной системе организации учебного процесса. Тематическое планирование составлено с учетом применения при обучении алгебре и началам анализа блочно-модульной технологии. Каждый тематический блок состоит из нескольких модулей: ПМ - проблемный модуль, ИМ - информационный модуль, РМ - расширенный модуль, МС - модуль систематизации, МКЗ - модуль коррекции знаний.
Модуль
|
Содержание модуля
|
Проблемный
|
Создание проблемной ситуации, приводящей к появлению нового понятия.
|
Информационный
|
Изучение нового материала единым блоком, разработка алгоритмов решения задач и классификация их основных типов.
|
Расширенный
|
Углубление и расширение теоретического материала. Решение более сложных, нестандартных задач
|
Систематизации
|
Обобщение и систематизация материала блока
|
Коррекции знаний
|
Ликвидация пробелов
|
Контроля
|
Учёт знаний учащихся:
а) текущий контроль;
б) контроль выполнения домашних заданий;
в) итоговый контроль.
|
Содержание программы
Интеграл (12ч)
Первообразная и неопределённый интеграл. Определённый интеграл, его вычисление и свойства. Вычисление площадей плоских фигур. Примеры применения интеграла в физике.
Функции (32ч)
Понятие корня энной степени из действительного числа. Функция у=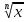 , её свойства и график. Понятие степени с рациональным показателем. Степенные функции, их свойства и графики. Показательная функция, её свойства и график. Понятие логарифма. Логарифмическая функция, её свойства и график. Производная показательной и логарифмической функций. , её свойства и график. Понятие степени с рациональным показателем. Степенные функции, их свойства и графики. Показательная функция, её свойства и график. Понятие логарифма. Логарифмическая функция, её свойства и график. Производная показательной и логарифмической функций.
Тождественные преобразования выражений (16ч)
Свойства корня n-ой степени и степени с рациональным показателем. Свойства логарифмов. Преобразование степенных выражений и выражений с радикалами. Преобразование показателей и логарифмических выражений.
Уравнения и неравенства (60ч)
Многочлены от одной переменной. Многочлены от нескольких переменных. Уравнения высших степеней. Равносильность уравнений и неравенств. Показательные уравнения и неравенства. Логарифмические уравнения и неравенства. Иррациональные уравнения и неравенства. Уравнения и неравенства с модулем. Системы уравнений и неравенств. Уравнения и неравенства с двумя переменными. Диофантовы уравнения. Уравнения и неравенства с параметрами.
Элементы комбинаторики теории вероятностей и математической статистики (9ч)
Вероятность и геометрия. Независимые повторения испытаний с двумя исходами. Статистические методы обработки информации. Гауссова кривая. Закон больших чисел.
Требования к уровню подготовки учащихся 10 – 11 классов
(профильный уровень)
В результате изучения математики на профильном уровне ученик должен:
знать
значение математической науки для решения задач, возникающих в теории и практике; широту и ограниченность применения математических методов к анализу и исследованию процессов и явлений в природе и обществе;
значение практики и вопросов, возникающих в самой математике, для формирования и развития математической науки;
идеи расширения числовых множеств как способа построения нового математического аппарата для решения практических задач и внутренних задач математики;
значение идей, методов и результатов алгебры и математического анализа для построения моделей реальных процессов и ситуаций;
возможности геометрии для описания свойств реальных предметов и их взаимного расположения;
универсальны характер законов логики математических рассуждений, их применимости в различных областях человеческой деятельности;
различие требований, предъявляемых к доказательствам в математике, естественных, социально-экономических и гуманитарных науках, на практике;
роль аксиоматики в математике; возможность построения математических теорий на аксиоматической основе; значение аксиоматики для других областей знания и для практики;
вероятностный характер различных процессов и закономерностей окружающего мира.
Числовые и буквенные выражения
уметь
выполнять арифметические действия, сочетая устные и письменные приёмы, применение вычислительных устройств; находить значения корня натуральной степени, степени с рациональным показателем, логарифма, пользоваться оценкой и прикидкой при практических расчетах;
применять понятия, связанные с делимостью целых чисел при решении математических задач;
находить корни многочленов с одной переменной, раскладывать многочлены на множители;
выполнять действия с комплексными числами, пользоваться геометрической интерпретацией комплексных чисел, в простейших случаях находить комплексные корни уравнений с действительными коэффициентами;
проводить преобразования числовых и буквенных выражений, включающих степени, радикалы, логарифмы и тригонометрические функции;
использовать приобретенные знания и умения в практической деятельности и повседневной жизни для практических расчётов по формулам, включая формулы, содержащие степени, радикалы, логарифмы и тригонометрические функции, используя при необходимости справочные материалы и простейшие вычислительные устройства.
Функции и графики
уметь
определять значение функции по значению аргумента при различных способах задагия функции;
строить графики изученных функций, выполнять преобразования графиков;
описывать по графику и по формуле поведение и свойства функций;
решать уравнения, системы уравнений неравенства, используя свойства функций и их графические представления;
использовать приобретенные знания и умения в практической деятельности и повседневной жизни для описания и исследования с помощью функций реальных зависимостей, представления их графически; интерпретации графиков реальных процессов.
Начала математического анализа
уметь
находить сумму бесконечно убывающей геометрической прогрессии;
вычислять производные и первообразные элементарных функций, применяя правила вычисления производных и первообразных;
исследовать функции и строить их графики с помощью производной;
решать задачи с применением уравнения касательной к графику функции;
решать задачи на нахождение наибольшего и наименьшего значения функции на отрезке;
вычислять площадь криволинейной трапеции;
использовать приобретенные знания и умения в практической деятельности и повседневной жизни для решения геометрических, физических, экономических и других прикладных задач, в том числе задач на наибольшие и наименьшие значения с применением аппарата математического анализа.
Уравнения и неравенства
уметь
решать рациональные, показательные и логарифмические уравнения и неравенства, иррациональные и тригонометрические уравнения, их системы;
доказывать несложные неравенства;
решать текстовые задачи с помощью составления уравнений, и неравенств, интерпретируя результат с учётом ограничения условия задачи;
изображать на координатной плоскости множества решений уравнений и неравенств с двумя переменными и их систем;
находить приближенные решения уравнений и их систем, используя графический метод;
решать уравнения, неравенства и системы с применением графических представлений, свойств функций, производной;
использовать приобретенные знания и умения в практической деятельности и повседневной жизни для построения и исследования простейших математических моделей.
Элементы комбинаторики, статистики и теории вероятностей
уметь
решать простейшие комбинаторные задачи методом перебора, а также с использованием известных формул, треугольника Паскаля; вычислять коэффициенты бинома Ньютона по формуле и с использованием треугольника Паскаля;
вычислять вероятности событий на основе подсчета числа исходов;
использовать приобретенные знания и умения в практической деятельности и повседневной жизни для анализа реальных числовых данных, представленных в виде диаграмм , графиков; для анализа информации статистического характера.
владеть компетенциями:
учебно-познавательной; ценностно-ориентированной; рефлексивной; коммуникативной; информационной; социально-трудовой.
Тематическое планирование
Модуль
|
Тема
|
Число уроков
|
|
Повторение материала 10 класса.
|
8
|
|
Блок №1 «Первообразная и интеграл»
|
12
|
ПМ
|
1.Понятие первообразной
|
1
|
ИМ
|
2.Основное свойство и правила вычисления
первообразных.
|
1
|
|
3.Неопределённый интеграл. Криволинейная трапеция.
|
1
|
|
4.Определённый интеграл
|
1
|
|
5.Вычисление интегралов.
|
2
|
РМ
|
6.Вычисление площадей фигур и объёмов тел с помощью интегралов.
|
6
|
МК
|
7. Контрольная работа №1
«Первообразная и интеграл»
|
1
|
|
Блок №2 «Функции»
|
32
|
ПМ
|
1.Графическое решение уравнений
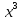 =а, =а, 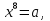 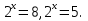
|
1
|
|
2.Понятие корня энной степени из действительного числа.
|
1
|
|
3.Функция у=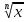 , её свойства и график. , её свойства и график.
|
2
|
|
4.Понятие степени с рациональным показателем.
|
1
|
|
5.Степенные функции, их свойства и графики.
|
3
|
|
6.Показательная функция, её свойства и график.
|
2
|
|
7.Понятие логарифма.
|
2
|
|
8.Логарифмическая функция, её свойства и график.
|
2
|
|
9.Производная показательной и логарифмической функций.
|
2
|
РМ
|
10.Построение графиков функций с использованием различных преобразований.
|
3
|
|
11. Графическое решение уравнений и неравенств.
|
3
|
|
12.Дифференцирование функций (у=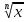 , степенной, показательной, логарифмической). , степенной, показательной, логарифмической).
|
3
|
МС
|
13.Сваойства функций, все элементарные функции.
|
2
|
МКЗ
|
14.Работа над пробелами по теме.
|
1
|
МК
|
15.Зачёт по теории.
|
1
|
|
16.Контрольная работа №2
«Функция у=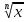 , степенные функции» , степенные функции»
|
1
|
|
17. Контрольная работа №3
«Показательная и логарифмическая функции».
|
2
|
|
Блок №3 «Тождественные преобразования выражений»
|
16
|
ИМ
|
1.Свойства корня энной степени и степени с рациональным показателем
|
2
|
|
2.Свойства логарифмов.
|
3
|
РМ
|
3.Преобразование степенных выражений и выражений с радикалами.
|
4
|
|
4.Преобразование показателей и логарифмических выражений.
|
4
|
МК
|
5.Релейная контрольная работа.
|
1
|
|
6.Контрольная работа №4
«Преобразование выражений».
|
2
|
|
Блок №4 «Уравнения и неравенства»
|
60
|
ПМ
|
1.Практическая значимость уравнений и неравенств.
|
1
|
ИМ
|
2.Многочлены от одной переменной.
|
2
|
|
3.Многочлены от нескольких переменных.
|
2
|
|
4.Уравнения высших степеней.
|
3
|
|
5.Равносильность уравнений и неравенств.
|
3
|
МК
|
6. Контрольная работа № 5
Многочлены и уравнения высших степеней.
|
2
|
|
7.Показательные уравнения и неравенств.
|
6
|
МК
|
8. Контрольная работа № 6
Показательные уравнения и неравенства.
|
2
|
|
9.Логарифмические уравнения и неравенства.
|
7
|
МК
|
10. Контрольная работа № 7
Логарифмические уравнения и неравенства.
|
2
|
|
11.Иррациональные уравнения и неравенства.
|
5
|
МК
|
12. Контрольная работа № 8
Иррациональные уравнения и неравенства.
|
1
|
|
13.Уравнения и неравенства с модулем.
|
5
|
МК
|
14. Контрольная работа № 9
Уравнения и неравенства с модулем.
|
1
|
|
15.Уравнения и неравенства с двумя переменными.
|
2
|
|
16.Системы уравнений и неравенств.
|
4
|
МК
|
17. Контрольная работа № 10
Системы уравнений и неравенств.
|
2
|
РМ
|
18. Нестандартные методы решения уравнений и неравенств.
|
8
|
МС
|
19.Общие способы решения основных типов уравнений и неравенств.
|
2
|
|
Блок №5 «Элементы теории вероятностей и математической статистики».
|
9
|
ИМ
|
1.Вероятночть и геометрия.
|
2
|
|
2.Независимые повторения испытаний с двумя исходами.
|
3
|
|
3.Статистические методы обработки информации.
|
2
|
|
4.Гауссова кривая. Закон больших чисел.
|
2
|
|
Блок №6 «Повторение».
|
67
|
|
1.Задачи с параметрами.
|
20
|
|
2.Тождественные преобразования выражений.
|
5
|
|
3.Уравнения и системы уравнений.
|
6
|
|
4.Решение текстовых задач.
|
4
|
|
5.Неравенства и системы неравенств.
|
6
|
|
6.Производная.
|
6
|
|
7.Решение упражнений на различные темы
|
20
|
|
ИТОГО
|
204
|
Осуществление представленной рабочей программы предполагает использование следующего учебно-методического комплекта:
А.Г. Мордкович, П.В. Семенов Алгебра и начала анализа 11 класс. Учебник для общеобразовательных учреждений (профильный уровень)– М. Мнемозина, 2007.
А.Г. Мордкович, Л.О. Денищева и др. Алгебра и начала анализа 11класс. Задачник для общеобразовательных учреждений (профильный уровень) под редакцией А.Г. Мордковича – М. Мнемозина, 2007.
В.И. Глизбург. Алгебра и начала анализа. Контрольные работы для11 класса общеобразовательных учреждений (профильный уровень). Под редакцией А.Г. Мордковича. – М. Мнемозина, 2008.
Л.О. Денищева, Т.А. Корешкова. Алгебра и начала анализа 10-11 классы. Тематические тесты и зачёты для общеобразовательных учреждений. Под редакцией А.Г. Мордковича. – М. Мнемозина, 2006.
А.П. Ершова. В.В. Голобородько. Самостоятельные и контрольные работы по алгебре и началам анализа для 10-11 класса. Разноуровневые дидактические материалы– М. Илекса, 2007
|
|
|
 Скачать 293.18 Kb.
Скачать 293.18 Kb.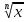 , её свойства и график. Понятие степени с рациональным показателем. Степенные функции, их свойства и графики. Показательная функция, её свойства и график. Понятие логарифма. Логарифмическая функция, её свойства и график. Производная показательной и логарифмической функций.
, её свойства и график. Понятие степени с рациональным показателем. Степенные функции, их свойства и графики. Показательная функция, её свойства и график. Понятие логарифма. Логарифмическая функция, её свойства и график. Производная показательной и логарифмической функций.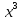 =а,
=а,