|
Мбоу сош №7 г. Лениногорска Республики Татарстан МБОУ СОШ № 7 г. Лениногорска Республики Татарстан
Проектная работа «Мини-задачники по теории вероятности и комбинаторике» Работу выполнили ученики 5 а класса Руководитель проекта: учитель математики Яхина Ольга Анатольевна
2012 год
Введение...............................................................................................................3
1.1.Теория вероятности – что это?………………….……...............................5
1.2. Эксперименты…………………………………………………………….…7
1.3. Можно ли выиграть в лотерею или рулетку? …………………..............9
2. Проект.………………………………………………….……………………11
Заключение .........................................................................................................21
Список литературы.............................................................................................22
Введение
Людей всегда интересовало будущее. Человечество во все времена искало способ его предугадать, или спланировать. В разное время разными способами. В современном мире есть теория, которую наука признает и пользуется для планирования и прогнозирования будущего. Речь о теории вероятностей.
В жизни мы часто сталкиваемся со случайными явлениями. Чем обусловлена их случайность – нашим незнанием истинных причин происходящего или случайность лежит в основе многих явлений? Споры на эту тему не утихают в самых разных областях науки. Случайным ли образом возникают мутации, насколько зависит историческое развитие от отдельной личности, можно ли считать Вселенную случайным отклонением от законов сохранения? Пуанкаре, призывая разграничить случайность, связанную с неустойчивостью, от случайности, связанной с нашим незнанием, приводил следующий вопрос: «Почему люди находят совершенно естественным молиться о дожде, в то время как они сочли бы смешным просить в молитве о затмении?»
У каждого 'случайного' события есть четкая вероятность его наступления. Например, посмотрите официальную статистику пожаров в России. Вас ничего не удивляет? Данные из года в год стабильные.
За 7 лет разброс от 14 до 19 тысяч погибших.Задумайтесь, пожар — событие случайное. Но можно с большой точностью предсказать сколько погибнет людей в пожаре в следующем году (~ 14-19 тысяч).
В стабильной системе вероятность наступления событий сохраняется из года в год. То есть, с точки зрения человека с ним произошло случайное событие. А с точки зрения системы, оно было предопределенно.
Разумный человек должен стремиться мыслить, исходя из законов вероятностей (статистики). Но в жизни о вероятности мало кто думает. Решения принимаются эмоционально.
Люди боятся летать самолетами. А между тем, самое опасное в полете на самолете — это дорога в аэропорт на автомобиле. Но попробуй кому-то объяснить, что машина опасней самолета. Вероятность того, что пассажир, севший в самолет, погибнет в авиакатастрофе - составляет примерно
1/8 000 000. Если пассажир будет садиться каждый день на случайный рейс, ему понадобится 21 000 лет чтобы погибнуть.
По исследованиям: в США в первые 3 месяца после терактов 11 сентября 2001 года погибло еще одна тысяч людей... косвенно. Они в страхе перестали летать самолетами и начали передвигаться по стране на автомобилях. А так как это опасней, то количество смертей возросло.
По телевидению пугают: птичьим и свиными гриппами, терроризмом..., но вероятность этих событий ничтожна по сравнению с настоящими угрозами. Опасней переходить дорогу по зебре, чем лететь на самолете. От падения кокосов погибает ~ 150 человек в год. Это в десятки раз больше, чем от укуса акул. Но фильма "Кокос-убийца" пока не снято. Подсчитано, что шанс человека быть подвергнутым нападению акулы составляет 1 к 11,5 млн., а шанс погибнуть от такого нападения 1 к 264,1 млн. Среднегодовое количество утонувших в США составляет 3306 человек, а погибших от акул 1. Миром правит вероятность и нужно помнить об этом. Они помогут вам взглянуть на мир с точки зрения случая.
В своей исследовательской работе я попробую проверить, действительно ли теория вероятности действует и как её можно применить в жизни.
Вероятность события в жизни не так уж часто считается по формулам, скорее интуитивно. Но проверить совпадает ли «эмпирический анализ» с математическим, иногда очень полезно.
1.1. Теория вероятности – что это?
Теория вероятностей или теория вероятности – это один из разделов Высшей Математики. Это самый интересный раздел Науки Высшая Математика Теория вероятности, которая являясь сложной дисциплиной, имеет применение в реальной жизни. Теория вероятностей представляет несомненную ценность для общего образования. Эта наука позволяет не только получать знания, которые помогают понимать закономерности окружающего мира, но и находить практическое применение теории вероятности в повседневной жизни. Так, каждому из нас каждый день приходиться принимать множество решений в условиях неопределенности. Однако эту неопределенность можно «превратить» в некоторую определенность. И тогда это знание может оказать существенную помощь при принятии решения. Изучение теории вероятностей требует больших усилий и терпения.
Теперь же давайте перейдем к самой теории и истории ее возникновения. Главным понятием теории вероятностей является вероятность. Это слово «вероятность», синонимом которого является, например, слово «шанс» достаточно часто применяется в повседневной жизни. Думаю, каждому знакомы фразы: «Завтра, вероятно, выпадет снег», или «вероятнее всего в выходные я поеду на природу», или «это просто невероятно», или «есть шанс получить зачет автоматом». Такого рода фразы на интуитивном уровне оценивают вероятность того, что произойдет некоторое случайное событие. В свою очередь математическая вероятность дает некоторую числовую оценки вероятности того, что произойдет некоторое случайное событие.
Теория вероятностей оформилась в самостоятельную науку относительно не давно, хотя история теории вероятностей началась еще в античности. Так, Лукреций, Демокрит, Кар и еще некоторые ученые древней Греции в своих рассуждениях говорили о равновероятностных исходах такого события, как возможность того, что вся материя состоит из молекул. Таким образом, понятие вероятности использовалось на интуитивном уровне, но оно не было выделено в новую категорию. Тем не менее, античные ученые заложили прекрасный фундамент для возникновения этого научного понятия. В средние века, можно сказать, и зародилась теория вероятности, когда были приняты первые попытки математического анализа, таких азартных игр как кости, орлянка, рулетка.
Первые научные работы по теории вероятностей появились в 17 веке. Когда такие ученые как Блез Паскаль и Пьер Ферма открыли некоторые закономерности, которые возникают при бросании костей. В ту же пору к данному вопросу проявлял интерес еще один ученый Христиан Гюйгенс. Он в 1657 в своей работе ввел следующие понятия теории вероятностей: понятие вероятности как величины шанса или возможности; математическое ожидание для дискретных случаев, в виде цены шанса, а также теоремы сложения и умножения вероятностей, которые правда не были сформулированы в явном виде. Тогда же теория вероятностей стала находить сферы своего применения – демографию, страховое дело, оценку ошибок наблюдений.
Дальнейшее развитие теории вероятностей привело к необходимости аксиоматизации теории вероятностей и главного понятия – вероятности. Так становление аксиоматики теории вероятностей произошло в 30 гг. 20 века. Самый существенный вклад в заложение основ теории внес Колмогоров А.Н.
На сегодняшний день теории вероятностей это самостоятельная наука, имеющая огромную сферу применения. В данном разделе сайта Вы найдете шпаргалки по теории вероятности, лекции и задачи по теории вероятностей, литературу, а также много интересных статей о применении теории вероятностей в жизни.
1.2. Эксперименты
Я решила проверить классическое определение вероятности.
Определение: Пусть множество исходов опыта состоит из n равновероятных исходов. Если m из них благоприятствуют событию A, то вероятностью события A называется число Р(А) = m/n.
Возьмем, к примеру, игру в монету. При бросании может быть два равновероятных исхода: монета может упасть кверху гербом или решкой. Бросая монету один раз нельзя предугадать, какая сторона окажется сверху. Однако, бросив монету 100 раз, можно сделать выводы. Можно заранее сказать, что герб выпадет не 1 и не 2 раза, а больше, но и не 99 и не 98 раз, а меньше. Число выпадений герба будет близко к 50. На самом деле, и на опыте можно в этом убедиться, что это число будет заключено между 40 и 60. Кто и когда впервые проделал опыт с монетой, неизвестно.
Французский естествоиспытатель Бюффон (1707-1788) в восемнадцатом столетии 4040 раз подбрасывал монету-герб выпал 2048 раз. Математик К.Пирсон в начале в начале нынешнего столетия подбрасывал ее 24 000 раз-герб выпал 12012 раз. Лет 20 назад американские экспериментаторы повторили опыт. При 10 000 подбрасываний герб выпал 4979 раз. Значит, результаты бросаний монеты, хотя каждое из них и является случайным событием, при неоднократном повторении подвластны объективному закону.
Проведём опыт. Для начала, возьмем в руки монетку, будем ее бросать и записывать результат последовательно в виде строки: О, Р, Р, О, О, Р. Здесь буквами О и Р обозначено выпадение орла или решки. В нашем случае бросание монетки – это испытание, а выпадение орла или решки – событие, то есть возможный исход нашего испытания. Проведя 100 испытаний орел выпал - 55, решка - 45.Вероятность выпадения орла в данном случае-0,55; решки – 0,45. Таким образом, я показала, что теория вероятности в данном случае имеет место быть.
Рассмотрим задачу с тремя дверьми и призами за ней: «Автомобиль или козлы»? или «парадокс Монти Холла». Условия задачи таковы:
Вы участвуете в игре. Ведущий предлагает выбрать одну из трех дверей и рассказывает о том, что за одной из дверей находится выигрыш – автомобиль, за двумя другими дверями спрятаны козы. После того, как Вы остановили свой выбор на одной из дверей, ведущий, который знает что находится за каждой дверью, открывает одну из оставшихся двух дверей и демонстрирует, что за ней находится козел (коза, пол животного в этом случае на так уж важен). А потом ведущий хитро так спрашивает: «Желаете ли Вы изменить свой выбор двери?» Увеличит ли изменение выбора шансы на выигрыш?
Если подумать: вот две закрытые двери, одну Вы уже выбрали и вероятность что за выбранной дверью автомобиль/коза 50% как и с подбрасыванием монетки. Но это совсем не так. Если поменять свое решение и выбрать другую дверь, то шансы выигрыша увеличатся в 2 раза! Опыт подтвердил данное утверждение. Т.е. оставив свой выбор, игрок получит автомобиль в одном из трех случаев, а поменяв двух из трех. Статистика телепередачи подтверждает, что те, кто менял свой выбор, выигрывали в два раза чаще.
Это все теория вероятности и она верна на «множестве вариантов». Надеюсь, что этот пример заставит вас задуматься, как быстро взять в руки книгу о теории вероятностей, а также начать ее применять в своей работе. Поверьте, это интересно и увлекательно, да и практический толк есть.
1.3. Можно ли выиграть в лотерею или рулетку?
Каждый из нас хоть раз в жизни покупал лотерею или играл в азартные игры, но далеко не все использовали заранее спланированную стратегию. Умные игроки давно перестали надеяться на удачу и включили рациональное мышление.
Дело в том, что каждое событие имеет определенное математическое ожидание, как гласит высшая математика и теория вероятности, и, если правильно оценивать ситуацию, то можно обойти неудовлетворительный исход события.
К примеру, в любой игре, такой, как рулетка, есть возможность играть с вероятностью на выигрыш 50%, ставя на выпадение четного числа, или красной ячейки. Вот как раз эту игру мы и рассмотрим.
Для обеспечения прибыли, составим несложную стратегию игры. К примеру, мы имеем возможность посчитать, с какой вероятностью выпадет четное число 10 раз подряд - 0,5*0,5 и так 10 раз. Умножаем на 100% и получаем всего 0,097%, или же, примерно, 1 шанс из 1 000.
Столько игр, пожалуй, сыграть вам не удастся и за всю свою жизнь, значит, вероятность выпадения 10 четных чисел подряд практически равна «0». Воспользуемся этой тактикой игры на практике.
Но это еще не все, даже 1 раз из 1 000 – это для нас много, так что сократим это число до 1 из 10 000. Вы спросите, каким образом это можно сделать, не увеличивая заранее предполагаемое количество выпадения четных чисел подряд? Ответ прост – время.
Подходим к рулетке и ждем пока выпадет 2 раза подряд четное число. Это будет каждый раз из четырех расчетных случаев. Теперь ставим минимальную ставку на четное число, к примеру 5р, и выигрываем по 5р за каждое выпадение четного числа, вероятность которого 50%.
Если же выпало нечетное, то увеличиваем следующую ставку в 2 раза, то есть ставим уже 10р. В этом случае вероятность проиграть будет равна 6%. Но не паникуйте, если даже в этот раз вы проиграете! Делайте повышение каждый раз в два раза больше. С каждым разом математическое ожидание на выигрыш увеличивается, и Вы в любом случае останетесь в прибыли.
Важно учесть тот факт, что эта стратегия подходит только для малых ставок, так как, изначально поставив большие деньги - Вы рискуете проиграть все из-за ограничений ставок в будущем. Если у Вас возникли сомнения по данной тактике, сыграйте с другом в угадывание стороны монеты на вымышленные деньги, ставя при проигрыше ставку в два раза больше.
Через время Вы убедитесь, что эта методика проста на практике и очень эффективна! Можно сделать вывод, что играя по данной стратегии, Вы не заработаете миллионы, а лишь выиграете себе на мелкие расходы.
Цель проекта.
1. Научиться решать комбинаторные задачи различными способами (метод древовидной схемы, метод графов, метод таблиц); научиться решать задачи на определение вида событий (достоверное, случайное, невозможное); на нахождение вероятности события.
2. Составить сборники задач по теории вероятности и комбинаторике.
Работу выполнили:
Абакумов Тимофей Николаевич
Азязов Вадим Валерьевич
Ахмадеев Самат Русланович
Ахметова Аделина Ильшатовна
Безлепкин Сергей Андреевич
Бузерова Елизавета Юрьевна
Воробьёва Мария Юрьевна
Гаврилова Татьяна Юрьевна
Галеева Алина Рашитовна
Галеева Ксения Игоревна
Гафарова Аделя Маратовна
Гизатуллина Кира Талгатовна
Гончарова Екатерина Валерьевна
Емельянов Алексей Валерьевич
Иванова Вероника Владиславовна
Исламов Марат Ильдарович
Лапаскина Ольга Вячеславовна
Мокеев Виталий Олегович
Мустаев Денис Александрович
Пимукова Елена Николаевна
Прокушкина Милана Витальевна
Салахова Айгуль Наилевна
Саримов Тимур Рафисович
Саярова Аделия Мансуровна
Стороженко Анна Евгениевна
Тайдакова Снежана Анатольевна
Эскина Кристина Валерьевна
Задачи по теории вероятности и комбинаторике.
 Жена попросила своего мужа купить лук, капусту и морковь. Какими различными способами муж мог совершить покупку? (Воробьева Маша)
 Записанный номер телефона из пяти цифр (5, 3, 4, 7, 2) оказался неверным. Необходимо определить варианты номера телефона. (Воробьева Маша)
 Иванова Вероника
 Гончарова Екатерина
 Лапаскина Ольга
 Галеева Ксения
 Стороженко Анна
В результате выполнения проектной работы был созданы задачники, который состоит из 10 задач и по теории вероятности, и по комбинаторике.
На уроках математики мы решали эти задачи, некоторые из них вызывали у нас затруднение.
Результат
Качество знаний при решении задач на составление уравнений до выполнение проектной работы составило 52%
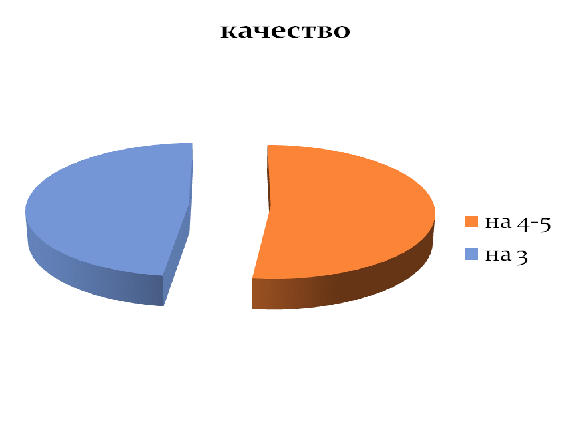
Качество знаний после решения задач из дидактического материала составило 67%.
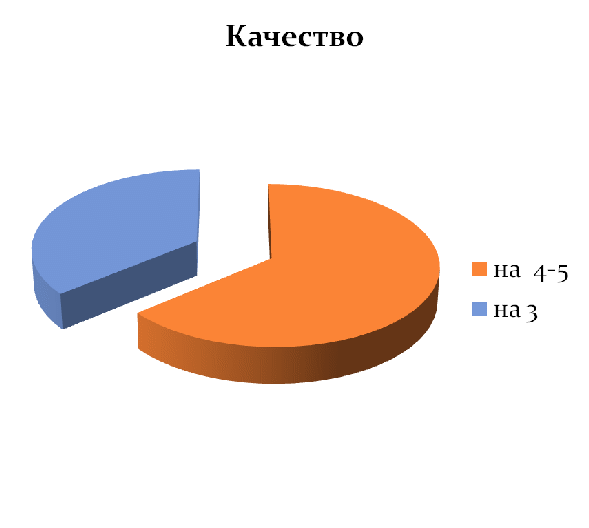
Качество знаний после решения задач из дидактического материала.
Заключение
Изучая тему «теории вероятности в жизни», я поняла, что это огромный раздел науки математики. И изучить его в один заход невозможно.
Перебрав множество фактов из жизни, и проведя эксперименты в домашних условиях, я поняла, что действительно теория вероятности в жизни имеет место быть. Вероятность события в жизни не так уж часто считается по формулам, скорее интуитивно. Но проверить совпадает ли «эмпирический анализ» с математическим, иногда очень полезно.
Можем ли мы предугадать с помощью этой теории, что случится с нами через день, два, тысячу? Конечно нет. Событий связанных с нами в каждый момент времени очень много. Только на одну лишь типизацию этих событий не хватит и жизни. А уж их совмещение — и вовсе гиблое дело. С помощью этой теории предугадывать можно лишь однотипные события. Например, такое как бросание монеты — это событие из 2 вероятностных результатов. В общем, прикладное применение теории вероятностей связанно с немалым количеством условий и ограничений. Для сложных процессов сопряжено с вычислениями, которые под силу лишь компьютеру.
Но следует помнить, что в жизни есть ещё такое понятие как удача, везение. Это то, что мы говорим - повезло, когда например какой-нибудь человек не учился никогда, никуда не стремился, лежал на диване, играл в компьютер, а через 5 лет мы видим как у него берут интервью на MTV. У него была вероятность 0.001 стать музыкантом, она выпала, ему повезло, такое схождение обстоятельств. То, что мы называем - оказался в нужном месте и в нужное время, когда срабатывают те самые 0.001.
Таким образом, работаем над собой, принимаем решения, которые могут повысить вероятность выполнения наших желаний и стремлений, каждый случай может добавить те заветные 0.00001, которые сыграют решающую роль в итоге.
Список литературы
https://yugzone.ru/subscribe/85.htm
https://blagodeteleva-vovk.com/theory/never.htm
https://sankt-petersburgpost.ru
https://habrahabr.ru/blogs/gtd/101695
https://dic.academic.ru
https://prosto.ws/2010/03/02/ot-teorii-veroyatnosti-k-teorii-vsego
https://mathematics.ru/courses/algebra/content/chapter4/section3/paragraph1/theory.html
|
|
|
Скачать 136.89 Kb.