|
Урок алгебры 10 кл учитель Кобзенко Е.Е.
Цель урока – развитие познавательной самостоятельности учащихся посредством
обучения их элементам математического моделирования.
Задачи урока:
Обучающие:
Ознакомление учащихся с математическими моделями, описывающими некоторые реальные процессы. Обеспечение усвоения новых математических понятий (простейшие тригонометрические уравнения и их решения) на уровне знания, понимания, применения, анализа и синтеза, оценки.
Развивающие:
Формирование у учащихся универсальных учебных действий:
личностных (действие смыслообразования), регулятивных (целеполагание, планирование, прогнозирование, самоконтроль),
познавательных (общеучебных – самостоятельное выделение и формулирование познавательной цели, выбор наиболее эффективных способов решения задач в зависимости от конкретных условий, знаково-символических – моделирование, преобразование модели.
коммуникативных (планирование и реализация учебного сотрудничества с учителем и сверстниками, постановка вопросов, управление поведением партнера).
Воспитывающие:
Содействие формированию научного мировоззрения, воспитанию умения преодолевать трудности, самостоятельности и инициативности.
Тип урока – урок закрепления нового материала.
Форма проведения урока – общеклассная дискуссия, работа в малых группах.
Методы обучения на уроке:
наглядно-модельное обучение (создание хорошо усваиваемых моделей, схем);
проблемное обучение (создание проблемных ситуаций, проблемно-поисковая беседа); применение ИКТ.
Ход урока:
Этап 1 Вводная беседа(3 мин)
Дидактические задачи - подготовка учащихся к работе на уроке.
Результат – полная готовность класса и оборудования, быстрое включение учащихся в деловой ритм урока.
|
В восточной философии существует эмблема двойственности инь-ян. Она изображается «совершенной фигурой»- кругом, символизирующим исходную целостность. Круг разделён на черную и белую симметричные половины, представляющие единство всех противоположностей мира(добра и зла, истины и лжи, земли и неба, темноты и света.)
Внутри каждой половины имеется круг другого цвета, что говорит о том, что противоположности проникают друг в друга.
Практически в любой математической задаче можно составить двойственную задачу: условия этих задач выражены различными наборами понятий, но решение их одинаково. Такие задачи_ это выражение одной и той же информации двумя различными способами(в явной и неявной форме)Давайте сегодня попробуем составить такую задачу на примере задачи В-12 из Открытого банка заданий ЕГЭ.
|
2 Этап Водное тестирование (3 мин)
|
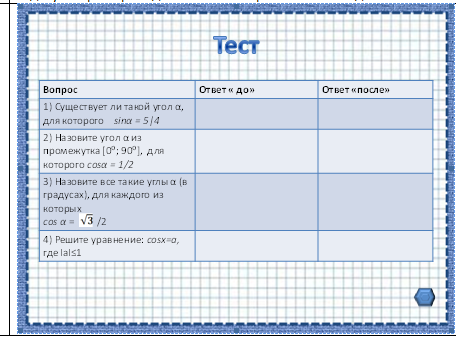
|
4 Этап Решение основной задачи. (5 мин)
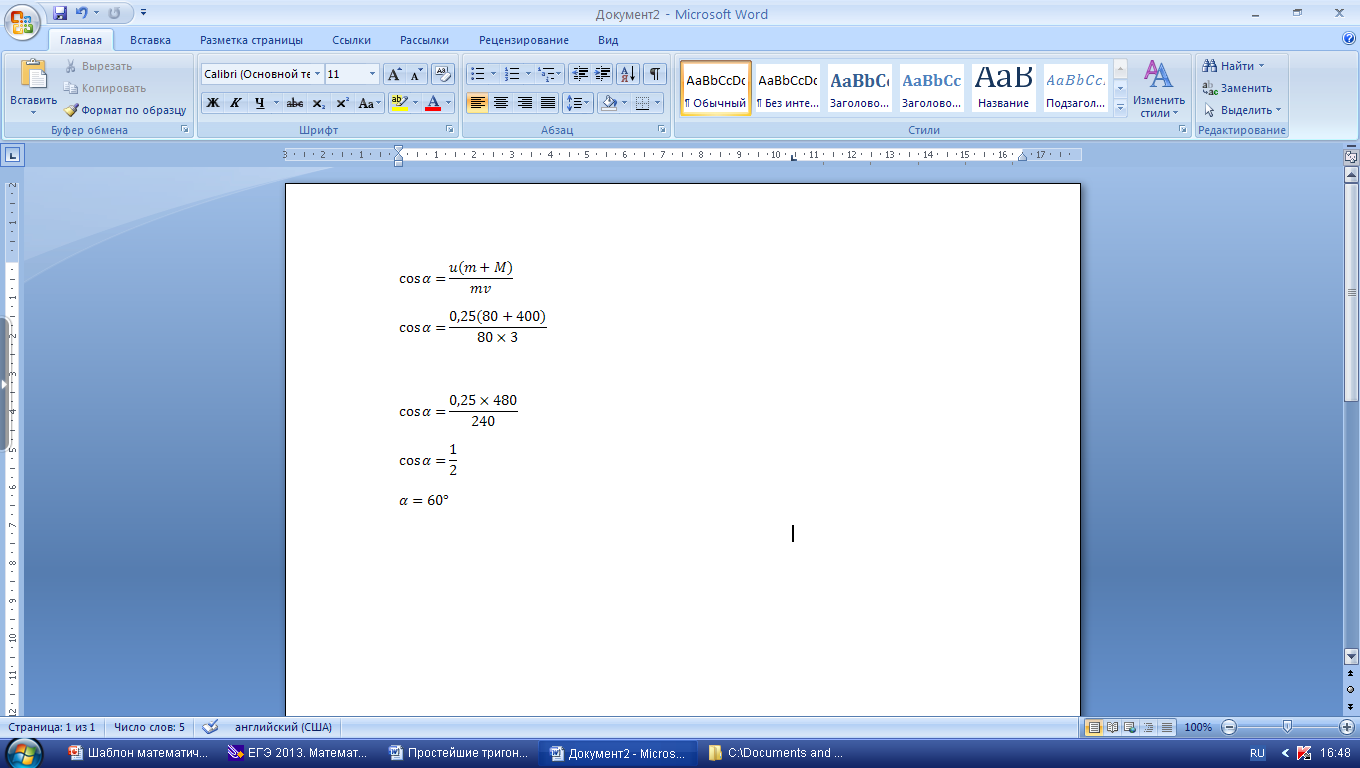
|
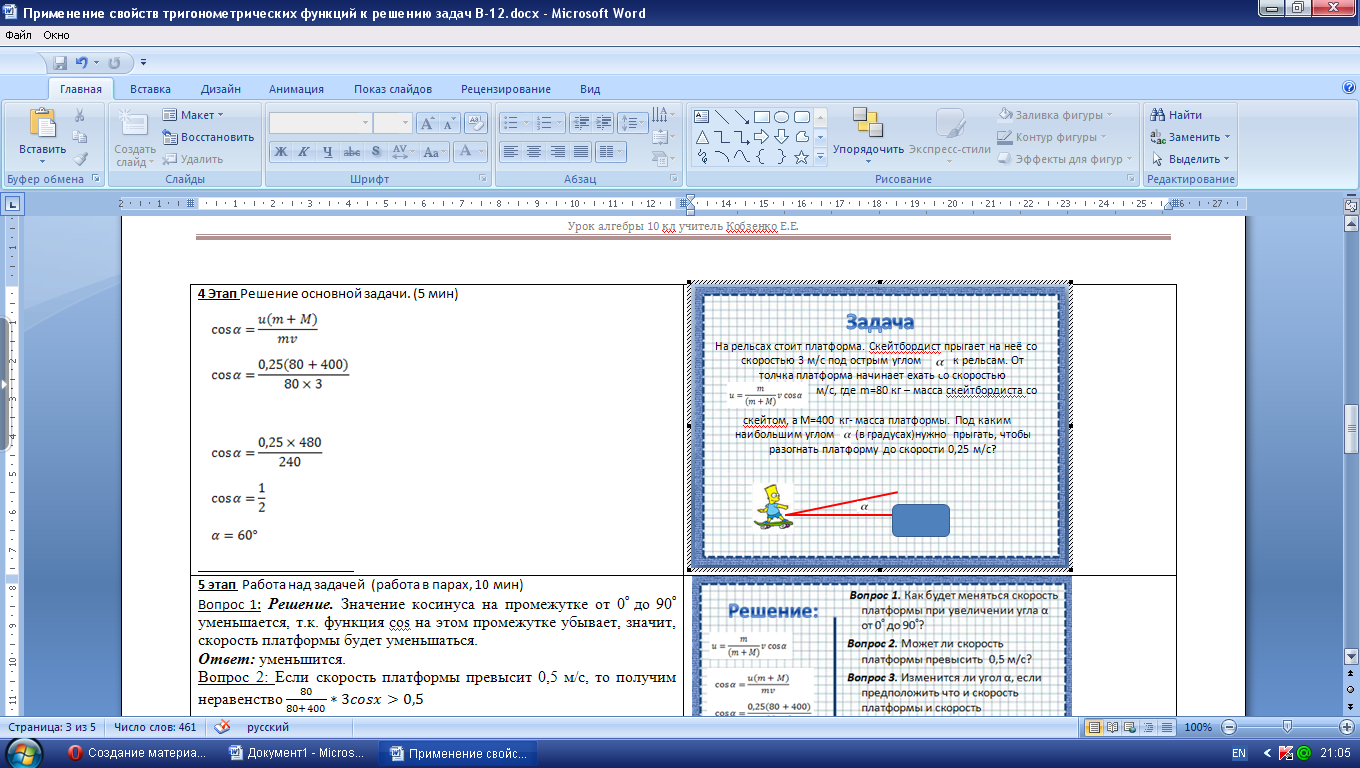
|
5 этап Работа над задачей (работа в парах, 10 мин)
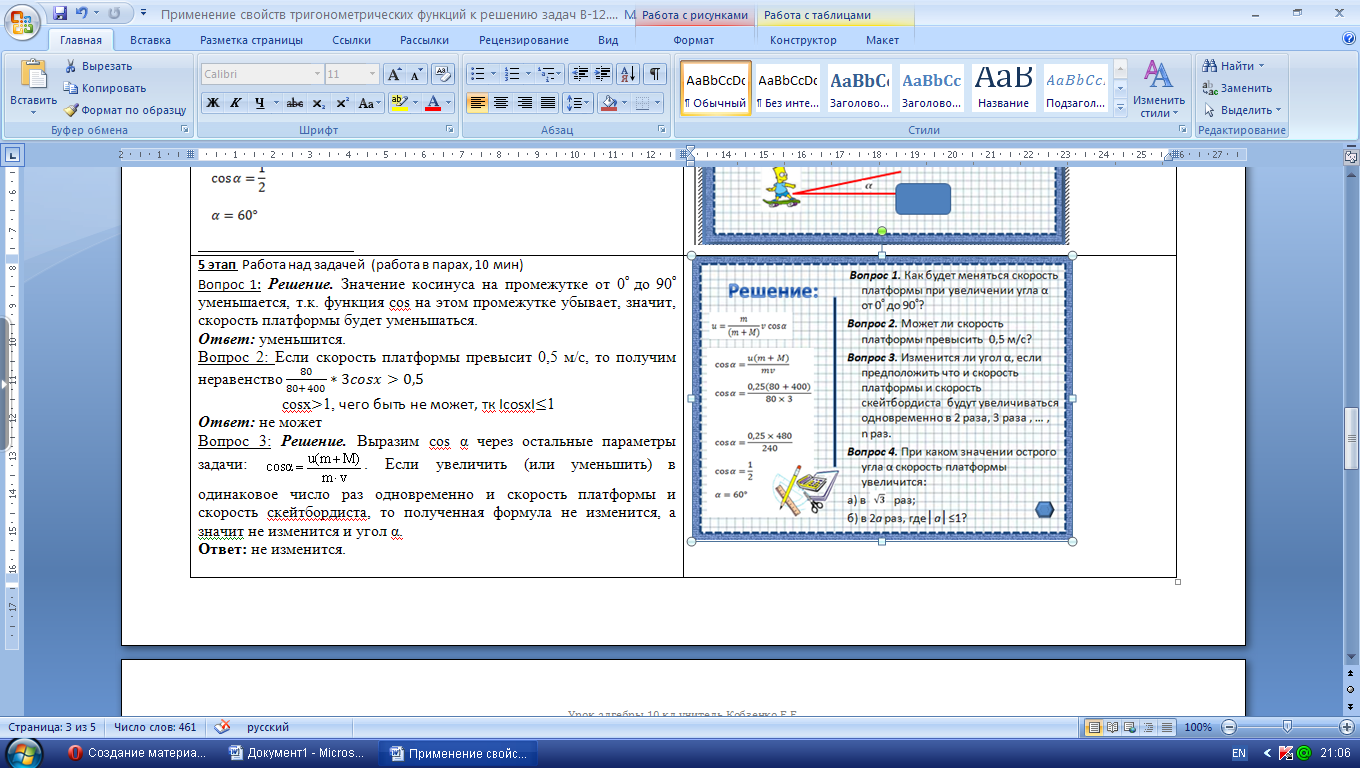
Вопрос 1: Решение. Значение косинуса на промежутке от 0⁰ до 90⁰ уменьшается, т.к. функция cos на этом промежутке убывает, значит, скорость платформы будет уменьшаться.
Ответ: уменьшится.
Вопрос 2: Если скорость платформы превысит 0,5 м/с, то получим неравенство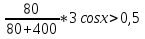
cosx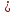 1, чего быть не может, тк IcosxI 1, чего быть не может, тк IcosxI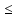 1 1
Ответ: не может
Вопрос 3: Решение. Выразим cos α через остальные параметры задачи: 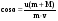 . Если увеличить (или уменьшить) в одинаковое число раз одновременно и скорость платформы и скорость скейтбордиста, то полученная формула не изменится, а значит не изменится и угол α. . Если увеличить (или уменьшить) в одинаковое число раз одновременно и скорость платформы и скорость скейтбордиста, то полученная формула не изменится, а значит не изменится и угол α.
Ответ: не изменится.
Вопрос 4:
а) 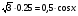
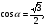
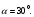
б) 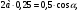
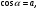
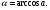
Ответ: а) 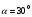 , б) , б) 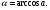
|
|
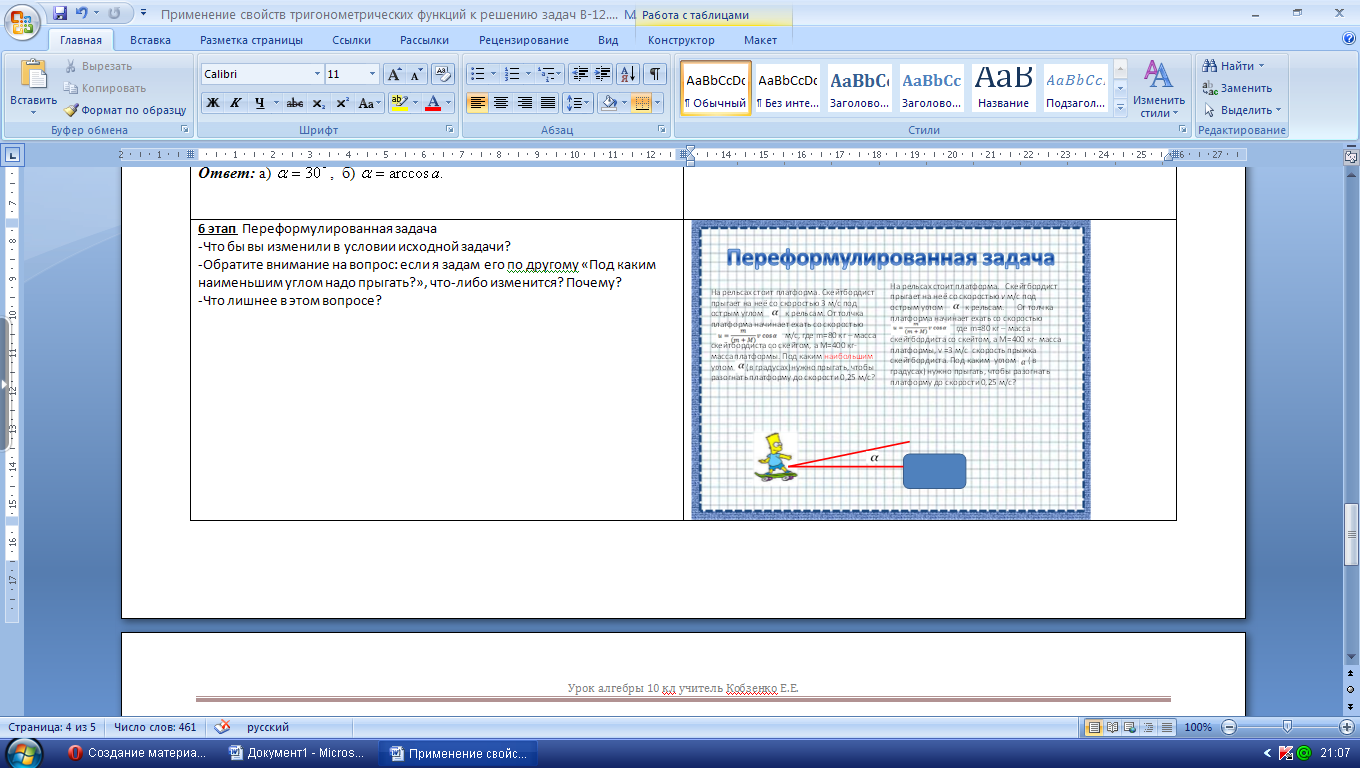
6 этап Переформулированная задача
-Что бы вы изменили в условии исходной задачи?
-Обратите внимание на вопрос: если я задам его по другому «Под каким наименьшим углом надо прыгать?», что-либо изменится? Почему?
-Что лишнее в этом вопросе?
|
|
7 этап Самопроверка опорных знаний
- Изменили ли вы своё мнение по какому-либо из вопросов?
- Проверка ответов на откидной доске.
|

| |
 Скачать 35.52 Kb.
Скачать 35.52 Kb.


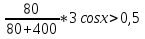
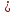 1, чего быть не может, тк IcosxI
1, чего быть не может, тк IcosxI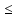 1
1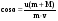 . Если увеличить (или уменьшить) в одинаковое число раз одновременно и скорость платформы и скорость скейтбордиста, то полученная формула не изменится, а значит не изменится и угол α.
. Если увеличить (или уменьшить) в одинаковое число раз одновременно и скорость платформы и скорость скейтбордиста, то полученная формула не изменится, а значит не изменится и угол α.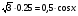
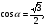
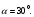
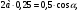
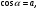
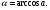
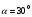 , б)
, б) 
