Рабочая программа по алгебре составлена: На основе примерной программы основного общего образования по математике (Сборник нормативных документов. Математика. М.: Дрофа, 2004)
 Скачать 80.76 Kb. Скачать 80.76 Kb. |
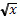  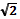  ПОЯСНИТЕЛЬНАЯ ЗАПИСКА Основной задачей обучения математике в школе является обеспечение прочного и сознательного овладения системой математических знаний и умений, необходимых в повседневной и трудовой деятельности каждому члену современного общества, достаточных для изучения и продолжения образования. Наряду с решением основной задачи углубленное изучение математики предусматривает формирование у учащихся устойчивого интереса к предмету, выявление и развитие их математических способностей, ориентацию на профессию, связанную с математикой, подготовку к обучению в вузе. Углублённое изучение математики в 8-9 классах является в значительной мере ориентационным. На этом этапе ученику надо помочь осознать степень своего интереса к предмету и оценить возможности овладения им, с тем, чтобы по окончанию 9 класса он мог сделать сознательный выбор в пользу либо дальнейшего углублённого, либо обычного изучения математики. Данная рабочая программа по алгебре составлена:
Сост.: Г.М. Кузнецова, Н.Г. Миндюк. М.: Дрофа, 2004,
Планирование исходит из учебного плана для школ и классов с углублённым изучением математики, согласно которому в основной школе изучаются два учебных предмета – алгебра (из расчета 5 учебных часа в неделю, всего 170 часов) и геометрия (3 часа в неделю, всего 102 часа). Программа
Предлагаемая программа учитывает общие и специфические цели углублённого изучения математики в целом и на каждом его этапе. Программа включает три раздела: «Требования к математической подготовке учащихся», «Содержание обучения», «Тематическое планирование». ТРЕБОВАНИЯ К МАТЕМАТИЧЕСКОЙ ПОДГОТОВКЕ Требования к знаниям и умениям учащихся при углублённом изучении математики не должны быть завышенными. Чрезмерная требовательность порождает перегрузку, что ведёт к угасанию интереса к математике. Поэтому требования к результатам углублённого изучения математики в 8-9 классах ненамного превышают требования общеобразовательной программы. Минимальный обязательный уровень подготовки, достижение которого учащимися является необходимым и достаточным условием выставления ему положительной оценки, при углублённом изучении и обычном изучении математики один и тот же. В результате изучения курса математики учащиеся должны:
СОДЕРЖАНИЕ ОБУЧЕНИЯ Множества и элементы комбинаторики. Множество. Элемент множества. Пустое множество. Пересечение и объединение множеств. Подмножество. Конечные и бесконечные множества. Число элементов объединения и пересечения двух конечных множеств. Взаимно-однозначное соответствие между множествами. Понятие о мощности множества. Принцип Дирихле. Комбинаторный принцип умножения. Число элементов прямого произведения двух множеств. Число подмножеств конечного множества. Число k-элементов подмножеств конечного множества из n элементов (число сочетаний). Число перестановок. Понятие вероятностного события. Подсчет вероятностей простейших событий. Числа и выражения. Натуральные числа. Делимость натуральных чисел. Признаки делимости на 2, 3, 4, 5, 9, 11. Простые и составные числа. Основная теорема арифметики. Бесконечность множества простых чисел. Взаимно простые числа. Наибольший общий делитель и наименьшее общее кратное. Нахождение наибольшего общего делителя. Алгоритм Евклида. Линейное представление наибольшего общего делителя. Критерий взаимной простоты двух чисел. Свойства множества натуральных чисел. Условие разрешимости уравнения a + x = b в множестве натуральных чисел и операция вычитания. Целые числа. Деление с остатком. Свойства множества целых чисел. Условия разрешимости уравнений вида ax = b в множестве целых чисел и операция деления. Рациональные числа. Свойства множества рациональных чисел. Выполнимость арифметических операций в множестве рациональных чисел и свойства этих операций. Числовые неравенства и их свойства. Задача измерения величин. Единица измерения. Измерение отрезков: единичный отрезок, процесс измерения. Общая мера двух отрезков. Соизмеримость и несоизмеримость отрезков. Связь между соизмеримостью отрезков и отношением их длин. Алгоритм Евклида для определения соизмеримости отрезков. Несоизмеримость диагонали квадрата с его стороной. Бесконечная десятичная дробь как результат измерения отрезка. Действительные числа как бесконечные десятичные дроби. Взаимно однозначное соответствие между множеством точек координатной прямой и множеством действительных чисел. Периодические десятичные дроби. Представление рационального числа в виде бесконечной периодической десятичной дроби. Примеры бесконечных непериодических десятичных дробей. Иррациональные числа. Свойства множества действительных чисел. Решение уравнения x2 = 2 множестве рациональных и в множестве действительных чисел. Квадратный корень. Условие существования квадратного корня и число квадратных корней из действительного числа. Арифметический квадратный корень. Иррациональность числа . Корень n–й степени. Выражения и их преобразования. Сложение, вычитание и умножение многочленов. Формулы сокращённого умножения: куб двучлена и квадрат алгебраической суммы нескольких слагаемых. Разложение многочлена на множители способом группировки. Формулы разложения на множители разности и суммы кубов, разности xn- yn и суммы x2k+1+ y2k+1. Многочлены с одной переменной. Квадратный трёхчлен. Выделение полного квадрата. Разложение квадратного трёхчлена на множители. Деление многочленов с остатком. Делимость многочленов. Теорема Безу и её следствие о делимости многочлена на линейный двучлен. Рациональные выражения. Основное свойство дроби. Сокращение дробей. Приведение дробей к общему знаменателю. Сложение, вычитание, умножение, деление и возведение в степень дробей. Тождественные преобразования рациональных выражений. Степень с целым показателем и её свойства. Стандартный вид числа. Свойства арифметических корней n-й степени. Свойства степеней с рациональными показателями. Преобразование выражений с радикалами и степенями с дробными показателями. Функции. Числовые функции. Способы задания функции. Область определения и область значений функции. Графики функции. Преобразования графиков функций: параллельный перенос, растяжение, сжатие вдоль осей координат, симметрия относительно осей координат и относительно прямой y = x. Свойства функции: возрастание и убывание, нули функции и промежутки знакопостоянства, наибольшее и наименьшее значение функции. Отражение свойств функции на графике. Элементарное исследование функции. Функция как соответствие между множествами. Элементарные функции: линейная, прямая и обратная пропорциональности, функции y = x2, y = x-2, y = . Их свойства и графики. Построение графиков кусочно – заданных функций. Построение графиков функций, связанных с модулем. Примеры построения графиков рациональных функций. Уравнения. Уравнение. Корень уравнения. Равносильность уравнений. Уравнение – следствие. Исключение «посторонних» корней. Линейное уравнение с одним неизвестным. Линейное уравнение с параметром. Квадратное уравнение: формула корней, зависимость числа корней от дискриминанта, формула Виета, составление уравнения с заданными корнями. Уравнения, сводящиеся к квадратным. Биквадратные уравнения. Решение рациональных уравнений. Системы уравнений. Решение систем уравнений. Равносильность. Приёмы решения систем: подстановка, алгебраическое сложение. Решение текстовых задач с помощью уравнений и систем. Неравенство с переменными. Числовые промежутки. Решение линейных неравенств с одной переменной и их систем. Основные понятия планиметрии. Неопределяемые понятия и аксиомы. Доказательства. Теоремы. Непротиворечивость системы аксиом. Исторические этапы развития геометрии: «Начала» Евклида, попытки доказательства пятого постулата, создание геометрии Лобачевского. Понятие о длине кривой. Площадь фигуры и её свойства. Равновеликость и равносоставленность фигур. Треугольники. Замечательные точки треугольника. Теорема Пифагора. Приложения теоремы Пифагора. Соотношения между сторонами и углами прямоугольного треугольника. Площадь треугольника. Формула Герона. Подобные треугольники. Теоремы Чевы и Менелая. Синус, косинус, тангенс и котангенс некоторых углов. Среднее геометрическое, среднее арифметическое, среднее гармоническое и среднее квадратичное для двух отрезков. Многоугольники. Понятие о многоугольнике. Площадь многоугольника. Параллелограмм и его свойства. Признаки параллелограмма. Прямоугольник, ромб, квадрат и их свойства. Трапеция и её свойства. Правильные многоугольники. Площади прямоугольника, параллелограмма, трапеции, правильного многоугольника Окружность и круг. Длина окружности. Площадь круга. Окружности, вписанные в треугольники и описанные вокруг треугольника. Вписанные и описанные четырёхугольники. Окружность Эйлера, окружности Аполлония. Терема Птолемея. Прямая Симпсона. Методы геометрии. Преобразование подобия. Подобие и его свойства. Отношения площадей подобных фигур. Признаки подобия треугольников. Применение подобия к решению задач. Векторы. Длина и направление вектора. Координаты вектора. Равенство векторов. Сложение и вычитание векторов, умножение вектора на число. Коллинеарные векторы. Разложение вектора по двум неколлинеарным векторам. Деление отрезка в данном отношении. Центр масс системы точек. Применение векторов к решению задач. Применение алгебры и тригонометрии к решению планиметрических задач. |