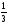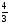| 1. /План.docx | Конспект урока «Объём шара и его частей». Никитюк Ирина Анатольевна гоу спо «Прохладненский Технологический колледж» Преподаватель Математика 1 курс
|
   План-конспект урока План-конспект урока
«Объём шара и его частей».
Никитюк Ирина Анатольевна
ГОУ СПО «Прохладненский Технологический колледж»
Преподаватель
Математика
1 курс.
А.В.Погорелов. Геометрия 7-11кл. М.:Просвещение, 2000.
Концептуальная цель преподавания геометрии: развитие логического и абстрактного мышления, пространственного воображения и исследовательских способностей.
Цель урока: развитие самостоятельности, гибкости мышления, точности и ясности математической речи.
9. Задачи:
Обучающие
* повторить формулы вычисления объемов цилиндра и конуса;
* дать понятие шарового сегмента, шарового слоя, шарового сектора;
* вывести формулу для вычисления объёма шара и его частей.
Развивающие:
*развитие аналитического и алгоритмического мышления; *совершенствование аудиального канала восприятия.
Воспитательные:
*познавательный интерес, коммуникативность;
*интуиция;
*эффективное внимание, самостоятельность.
10.Тип урока: Проблемная лекция.
Проблема. Внутренний диаметр чугунного полого шара, равен 8 см., а его внешний диаметр 10 см. Определите массу шара, если плотность чугуна 7,3 г/см3.
Проблемный вопрос: как можно вычислить объём шара?
Варианты решений:
1. закон Архимеда;
2. принцип Кавальери;
3.интегральная формула.
Оптимальный вариант: варианты 2 – 3 дают возможность получить формулу V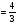 ΠR3, а с помощью закона Архимеда можно вычислить объём тела практически. ΠR3, а с помощью закона Архимеда можно вычислить объём тела практически.
11. Формы работы: фронтальная
12. Техническое оборудование: мультимедийный проектор, компьютер.
13.Структура и ход урока.
Таблица 1.
СТРУКТУРА И ХОД УРОКА
№
|
Этап урока
|
Название используемых ЭОР
|
Деятельность преподавателя
|
Деятельность студента
|
Время
(в мин.)
|
1
|
2
|
3
|
5
|
6
|
7
|
1
|
Формулировка заданий
|
Модуль 7,8
|
Формулировка цели урока
|
Знакомятся с заданиями, задают вопросы
|
5 мин.
|
2.
|
Работа с заданием
|
|
Урок начинается с рассмотрения задачи: «Как вычислить объём металлического шарика, используя линейку и прозрачный цилиндрический сосуд с водой». В ходе решения опираемся на закон Архимеда.
|
Выполняют данную задачу практически, с записью необходимых вычислений.
|
10мин
|
3.
|
Проверка выполнения задания
|
|
Проверка результатов, подведение итогов, вывод.
|
Представляют результаты
|
|
4.
|
Вывод формулы объёма.
|
|
Рассмотрим несколько подходов к выводу формулы для вычисления объема шара.
Вывод формулы V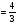 ΠR3 с помощью принципа Кавальери. ΠR3 с помощью принципа Кавальери.
В 17 веке началась эпоха интегрального исчисления. Математики возвращались к задачам о вычислении площадей криволинейных фигур и объёмов «кривых» тел, которыми так успешно занимался в древности Архимед. Интересовался этим вопросом и итальянский монах Бонавентура Кавальери (1598 – 1647). Он возглавлял кафедру математики в Болонском университете. Кавальери разработал способ, с помощью которого можно вычислять площади многоугольников, криволинейных фигур. Очень удобен принцип Кавальери и для получения формул объёмов круглых тел, например шара. Принцип Кавальери состоит в том, что если пересечь тело плоскостями, параллельными
|
Слушают, делают записи в тетрадях, формулируют вопросы преподавателю
|
|
|
|
|
некоторой заданной плоскости, то его объём определяется площадями пересечений плоскостей и тела.Для этого впишем в круговой цилиндр радиусом R и высотой 2R шар. Тело, являющееся дополнением шара до цилиндра, по принципу Кавальери, равновелико телу, составленному из двух конусов, построенных на верхнем и нижнем основаниях цилиндра с вершиной в центре шара. Отсюда следует:
Vш = Vц – 2Vк
Vц = Пr2h, где h = 2r
Vц = 2Пr3
Vк = 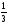 Пr2h, где h = r Пr2h, где h = r
Vк = 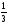 Пr3 Пr3
Vш = 2Пr3 – 2 · 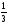 Пr3 = Пr3 = 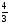 Пr3 Пr3
|
|
7мин
|
5.
|
Решение проблемы сформулированной в начале урока.
|
|
Решаем задачу. В процессе совместного обсуждения выходим на оптимальный вариант решения проблемы.
|
Выполняют данную задачу практически, с записью необходимых вычислений.
|
5мин
|
6.
|
Вводятся новые понятия: шаровой сегмент, шаровой слой, шаровой сектор.
|
Модуль 3-6,8
|
Даёт пояснения, дополняет.
|
Слушают, делают записи в тетрадях.
|
5мин
|
7.
|
Решение задач для самоконтроля.
|
Модуль 10,11.
|
Проверка результатов, подведение итогов.
|
Представляют результаты
|
7мин
|
8.
|
Обобщение, подведение итогов урока,
|
Модуль 10
|
Задаёт вопросы.
|
Отвечают.
|
3мин
|
9.
|
Рефлексия.
|
|
Отрефлексируйте своё эмоциональное состояние с помощью шкалы настроения:
|
Выбирают.
|
2мин
|
Таблица 2.
ПЕРЕЧЕНЬ ИСПОЛЬЗУЕМЫХ НА ДАННОМ УРОКЕ ЭОР
№
|
Название ресурса
|
Тип, вид ресурса
|
Форма предъявления информации
|
Гиперссылка на ресурс, обеспечивающий доступ к ЭОР
|
1.
|
Формулы площади боковых поверхностей цилиндра, конуса. Формулы объёмов цилиндра, конуса.
|
И
|
Иллюстрация, видеофрагменты, звук
|
https://fcior.edu.ru/card/27983/cilindr-i-konus.html
|
2.
|
Объём шара. Объём шарового сегмента, шарового слоя.
|
И1
|
Иллюстрация, видеофрагменты,
|
https://fcior.edu.ru/card/5015/obem-shara-obem-sharovogo-segmenta-sharovogo-i1.html
|
3
|
Решение задач для самоконтроля.
|
И1
|
Иллюстрация, видеофрагменты,
|
https://fcior.edu.ru/card/5015/obem-shara-obem-sharovogo-segmenta-sharovogo-i1.html
|
4
|
Объём шара. Объём шарового сегмента, шарового слоя.
|
И1
|
Иллюстрация, видеофрагменты, звук, анимация.
|
https://fcior.edu.ru/card/5015/obem-shara-obem-sharovogo-segmenta-sharovogo-i1.html
| |
 Скачать 61.74 Kb.
Скачать 61.74 Kb.

 План-конспект урока
План-конспект урока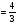 ΠR3, а с помощью закона Архимеда можно вычислить объём тела практически.
ΠR3, а с помощью закона Архимеда можно вычислить объём тела практически.