|
Конспект урока «Линейная функция и её график» фио (полностью) Рихтер Анна Николаевна Место работы
ПЛАН-КОНСПЕКТ УРОКА
«Линейная функция и её график»
|
ФИО (полностью)
|
Рихтер Анна Николаевна
|
|
Место работы
|
ГБОУ СОШ №8 г.о. Отрадный
|
|
Должность
|
учитель математики
|
|
Предмет
|
алгебра
|
|
Класс
|
7
|
|
Тема и номер урока в теме
|
Линейная функция и ее график, №3
|
|
Базовый учебник
|
Учебник Алгебра. 7 класс. Ю.Н. Макарычев, Н.Г. Миндюк, К.Н. Нешков, С.Б. Суворова Ю.Н, 2009
|
Цель урока: Закрепить и систематизировать знания учащихся по теме «Линейная функция и её график»
9. Задачи:
- обучающие
Способствовать закреплению навыка использования теоретических знаний по теме на практике, а именно: строить графики линейных функций, находить координаты точек пересечения графиков функций разными способами;
Способствовать осознанию и закреплению учебного мате�риала с помощью его визуализации на интерактивной доске;
-развивающие
Способствовать развитию у школьни�ков умения отвечать на вопросы учи�теля по изученному материалу;
Способствовать развитию у школь�ников умения определять черты сходства и различия в уравнениях графиков функций;
Развивать умение определять расположение графика функции в координатной плоскости, не выполняя его построения;
- воспитательные
Способствовать формированию интереса к предмету и логического мышления через решение нестандартных задач.
Тип урока: Закрепления знаний по теме «Линейная функция и её график»
Формы работы учащихся: фронтальная, индивидуальная.
Техническое оборудование: компьютер, проектор, интерактивная доска.
СТРУКТУРА И ХОД УРОКА
№
|
Этап урока
|
№ слайда
|
Деятельность учителя
|
Деятельность ученика
|
Время
(в мин.)
|
1
|
1
|
2
|
3
|
4
|
5
|
1
1
|
Организационный момент
|
|
Приветствует учащихся, объявляет тему урока и план работы в течение урока.
|
Приветствуют учителя и знакомятся с темой и планом урока.
|
2
|
2
2
2
|
Целеполагание и мотивация
|
|
Чтобы вспомнить основные понятия решим анаграммы ФФИИЦЭОКТНЕ, АЯРПЯМ, ИКАРФГ, АНЛИЯНЕЙ, КЦНУФЯИ, НТАРУГМЕ.
Что объединяет данные слова?
Те ребята, которые в будущем мечтают стать врачами, космонавтами, инженерами, в своей работе постоянно будут иметь дело с графиками и поэтому должны уметь их строить и читать. И наша задача изучить данную тему на хорошем уровне.
|
Ответы: коэффициент, прямая, график, линейная, функция, аргумент.
Все слова связаны с темой «Функции»
|
5
|
3
3
|
Актуализация (устная работа)
|
|
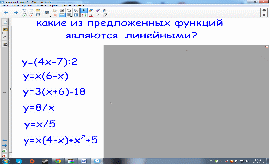
1.Какие из предложенных функций являются линейными, укажите, не выполняя построения графиков.
С последующей проверкой.
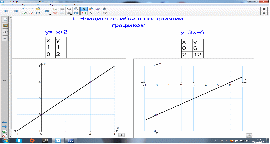
2.Найди ошибку в построении графика.
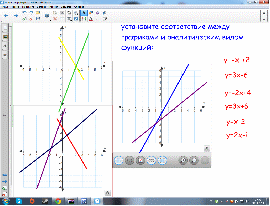
3.Установите соответствие между графиком и аналитическим видом функции.
4.не выполняя построения, определите взаимное расположение графиков функций и укажите значения коэффициентов к;в.
Являются ли функции линейными? Если да, то найдите коэффициенты k и b.
|
На выполнения задания даётся 1 минута, после чего ребята выполняют самопроверку.(ответы проверяются открытием шторки)
На обдумывание даётся 1 минута, после чего ребята отвечают и устно поясняют свои ответы.
Задания распределены по рядам, каждому ряду по 2 графика, после минутного обдумывания каждый ряд даёт свои ответы.
Используется эффект появления ответов.
|
7
|
4
|
Об ъяснение материала
|
|
Открываем тетради, записываем число, Классная работа. Тема урока: Линейная функция и её график.
Сегодня на уроке мы будем выполнять задания, типа: «пересекаются ли графики функций?», если пересекаются, то определять координаты точки пересечения.
Сначала рассмотрим в общем виде решение заданий такого типа: Представим, что даны два графика функций у=k1x+b1 и y=k2x+b2. Нужно выяснить пересекаются они или нет. Если пересекаются, то найти точку пересечения.
Решение:1этап: Проверить, параллельны они или нет, если параллельны, то сделать вывод, что не пересекаются.Два графика будут параллельны,если коэффициенты перед х равны, т.е. у=kх+b1, у=kх+b2. Например, у=12х-4 и у=12х+2, параллельны, т.е. не пересекаются, так как k1=12, k2=12, k1=k2;у=4х и у=8х-1 – не параллельны, т.к. k1=4, k2=8, k1≠k2.
2 этап.
1 способ. Графический.
Построить оба графика в одной системе координат и продолжить их до пересечения. Найти координаты точки пересечения. Если координаты точки – дробные числа, то этот способ будет не точным.
2 способ. Аналитический.
Составить уравнение k1x+b1=k2x+b2 и решить его. Таким образом, мы найдем абсциссу х0 точки пересечения, затем подставить в любое уравнение это число вместо х и вычислить ординату у0 точки пересечения.
Затем сделать вывод, что графики пересекаются в точке с координатами (х0; у0).
|
Выполняют упражнения повторяя за ведущим, находясь около своих парт
Записывают в тетрадях число, Классная работа, Тема урока: Линейная функция и её график.
Записывают алгоритм выполнения заданий такого типа.
|
5
|
5
|
Осознание и осмысление учебной информации
|
|
Выполним задания по алгоритму:
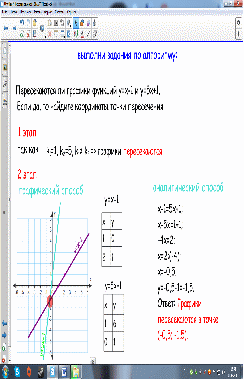
Задание 1. Пересекаются ли графики функций у=х-1 и у=2х+1. Если пересекаются, то найти точку пересечения.
1 этап.
Проверить, параллельны они или нет, если параллельны, то делаем вывод, что не имеют общей точки пересечения.
Два графика будут параллельны, если коэффициенты перед х равны, т.е. у=kх+b1, у=kх+b2.
у=х-1 и у=5х+1 – не параллельны, т.к. к1=1, к25, k1≠k2.
2 этап.
1 способ. Графический.
Построить оба графика в одной системе координат и продолжить их до пересечения.
2 способ. Аналитический.
Составляем уравнение и решаем его:
х-1=5х+1
х-5х=1+1
-4х=2
х=2:(-4)
х=-0,5
у=-0,5-1=-1,5
Координаты точки пересечения
(-0,5;-1,5)
Ответ: пересекаются в точке
(-0,5;-1,5).
|
Записывают пример в тетрадь, задают вопросы учителю.
Особое внимание обращаем на неточность графического способа решения данных заданий.
|
6
|
6
|
Первичное закрепление учебного материала
|
|
Задание 2. Пересекаются ли графики функций у=-2х+3 и у=3х+1. Найти координаты точки пересечения.
Задание 3. Пересекаются ли графики функций у=3х-2 и у=3х+1. Найти координаты точки пересечения.
Задание 4. Пересекаются ли графики функций у=х+1 и у=7х-3. Найти координаты точки пересечения.
Задание 5. Пересекаются ли графики функций у=5х-7, у=4х-6 и у=18? Найти координаты точек пересечения.
|
Выполняют задания, 1 человек у доски, остальные на месте.
После завершения выполнения задания на доске, учащийся может проверить себя(на экране появляется правильный ответ после прикосновения к объекту)
|
10
|
7
|
Постановка домашнего задания и подведение итогов урока.
|
|
№327, 328, 329.
В заключении урока прошу отметить смайликом своё настроение .
|
Записывают домашнее задание в дневники.
Прикрепляют смайлики в своих работах.
|
2
| |
|
|
 Скачать 86.95 Kb.
Скачать 86.95 Kb.










