Организация исследовательской работы
 Скачать 191.84 Kb.
|
ОРГАНИЗАЦИЯ ИССЛЕДОВАТЕЛЬСКОЙ РАБОТЫ НА УРОКАХ МАТЕМАТИКИ Содержание Введение………………………………………………………………..3 Понятие исследовательской деятельности обучающихся ………….4 Организация исследовательской работы на уроках математики …..5 Исследовательская деятельность старшеклассников ………………8 Заключение…………………………………………………………….12 Литература……………………………………………………………..13 Приложения……………………………………………………………14 Введение Современное состояние российского образования характеризуется появлением большого количества новых образовательных технологий и программ. При этом в Концепции модернизации российского образования на период до 2010 года особое внимание уделяется вопросу создания условий для повышения качества общего и профессионального образования [7]. «Базовое звено образования – общеобразовательная школа, модернизация которой предполагает ориентацию образования не только на усвоение обучающимися определенной суммы знаний, но и на развитие его личности, его познавательных и созидательных способностей. Общеобразовательная школа должна формировать целостную систему универсальных знаний, умений, навыков, а также опыт самостоятельной деятельности и личной ответственности обучающихся, т. е. ключевые компетенции, определяющие современное качество содержания образования». Академик Александров А. Д. отмечает, что «…цель школьного образования состоит в том, чтобы дать человеку основные практически нужные знания и развить его личность». Образование на современном этапе предполагает создание условий для реализации творческого потенциала учащихся, условий, при которых вместе с накоплением и применением знаний развивались бы склонности, способности ученика. Основная задача школы – научить ученика учиться, научить добывать новое знание, приходить к открытию новых истин. Решению этой задачи способствует применение элементов исследовательской технологии в образовательном процессе [7]. Данная работа является попыткой обобщить опыт по применению элементов исследования на уроках математики и во внеурочное время как в среднем звене, так и в профильной школе. Понятие исследовательской деятельности обучающихся («договоримся о терминах!») Исследовательская технология предполагает включение учащихся в учебно-исследовательскую деятельность. Под учебно-исследовательской деятельностью учащихся понимается процесс решения ими научных проблем, имеющий своей целью построение субъективно нового знания. Учебное исследование сохраняет логику научного исследования, но отличается от него тем, что не открывает объективно новых для человечества знаний.[7] Прежде всего хотелось бы разделить понятия: исследования и проекты, учебное исследование и научное исследование. Исследовательская деятельность обучающихся – деятельность учащихся, связанная с решением учащимися творческой, исследовательской задачи с заранее неизвестным решением и результатом. Предполагает наличие основных этапов, характерных для исследования в научной сфере. Постановка проблемы, изучение теории, подбор методик исследования, сбор собственного материала, его анализ и обобщение, научный комментарий, собственные выводы. Такая цепочка является неотъемлемой принадлежностью исследовательской деятельности, нормой её поведения. Проектная деятельность обучающихся – совместная учебно-познавательная, творческая или игровая деятельность учащихся, имеющая общую цель, согласованные методы, способы деятельности, направленная на достижение общего результата. Непременным условием проектной деятельности является наличие заранее выработанных представлений о конечном продукте деятельности, этапов проектирования. Выработка концепции, определение целей и задач проекта, создание плана, программ и организации деятельности по реализации проекта (включая его осмысление и рефлексию результатов деятельности). Сегодня о научно-исследовательской деятельности говорят, смешивая ее с проектной, но это не совсем верно, поскольку исследование на выходе имеет новое знание, а проектная деятельность – продукт, направленный на изменение реальной ситуации, пусть и виртуальной. Научно-исследовательская деятельность – иной вид деятельности, ориентированный на другие типы результатов. В ней формируются именно исследовательские навыки – анализа, сравнения и сопоставления, формулирования и доказательства гипотез и т. д. [6] Организация исследовательской работы на уроках математики («взгляд критический, но оптимистический») В последнее время говорить о проектно-исследовательских технологиях в школе стало «модным». В серьезных изданиях появляются серьезные статьи, материалы которых убеждают учителя в использовании этих технологий на уроках. Однако учителя не спешат применять то, о чем сами они имеют достаточно приблизительное понятие, им хочется конкретики: планов уроков, методик, дидактических материалов, мастер-классов(!), учебных пособий и так далее. Ведь проектная деятельность, а тем более исследовательская, предполагает не только блестящее владение материалом для учителя, но и прочных базовых знаний - для ученика! В современном мире (и это ни для кого не секрет!) мотивация детей к учебе снижена, потребность в качественных знаниях отсутствует, так как наличие этих знаний не гарантирует их обладателям успешности в жизни и профессиональной деятельности. Усиление мотивации к учебе, пробуждение интереса к ней – это и есть, по моему мнению, цель использования в преподавании проектно-исследовательских технологий. Однако это использование должно быть разумным, дополняющим традиционный урок, а не подавляющим его. Для такой отрасли знаний, как математика, это еще более важно. При всем моем настороженном отношении к проектам и исследованиям на уроках математики, им все же можно найти применение. Возможно, их место на моих уроках будет гораздо скромнее, чем у моих коллег (историков, филологов, естественников), все-таки мой предмет требует, прежде всего, умений и навыков, однако, есть область, где проекты и исследования будут как нельзя более кстати. В последние десять лет такой школьный предмет, как геометрия, постигла настоящая катастрофа. При бесконечной чехарде программ, сокращении часов и, одновременно, росте требований к знаниям абитуриентов (посмотрите задания ЕГЭ в части стереометрии!) происходит стремительное падение интереса учеников к этому предмету и, как следствие, снижение качества их знаний. В рейтинге школьных дисциплин подавляющее большинство учащихся 7 – 11 классов ставит геометрию на последнее место! Великий (не побоюсь этого слова!) российский математик и педагог И. Ф. Шарыгин, назвавший геометрию «витамином для мозга», видел выход в раннем изучении геометрии, начиная с 5-6 класса, но геометрии наглядной, с множеством красивых чертежей, практических и лабораторных работ. При изучении такой наглядной геометрии разумно и необходимо приучать детей (постепенно!) к самостоятельной исследовательской работе. Мною разработана и апробирована программа для раннего изучения геометрии в 5-6 классе, которая предполагает достаточно большое количество уроков-исследований наряду с лабораторными работами. Возможно ее использование совместно с учебниками И. И. Зубаревой «Математика 5,6», по которым работают учителя математики «Гимназии №87». В данной программе большое внимание уделяется практической работе учащихся. При изучении соответствующих разделов проводятся 4 лабораторные работы, которые помогают лучше освоить программный материал. Для проверки знаний учащихся разработаны 4 контрольные работы, а также тестовые задания по всем основным разделам программы. Отличительной особенностью данной программы является ее мировоззренческая направленность, т.е. изучение предмета геометрии в тесной связи с изучением окружающего мира, ознакомление с пространственными представлениями о мире, изучение размерности для последовательного развития этих представлений. Приведу пример карточки одной из лабораторных работ (приложение 1). Учащиеся пятых и шестых классов занимаются геометрией с восторгом! Интересный, посильный, но необычный материал, возможность творческой работы (найти, измерить, выдвинуть гипотезу, доказать, сделать вывод), использование ресурсов интернета, энциклопедий, эстетическое удовольствие от красивых чертежей и рисунков – вот причины, по которым предмет очень нравится школьникам. Если нет возможности преподавать геометрию как учебный предмет, всегда существует возможность сделать это на занятиях кружка или факультатива. Что мы будем иметь «на выходе»? Умение выполнять простые чертежи, в том числе и стереометрические, предполагающее рациональное использование тетрадного листа, твердое знание свойств простейших геометрических фигур, навыки самостоятельной деятельности по анализу этих свойств. Кроме того, формируется представление о геометрии как об увлекательном предмете, имеющем каждодневное практическое применение. «Я думаю, что никогда до настоящего времени мы не жили в такой геометрический период. Все вокруг – геометрия» (Ле Корбюзье, великий французский архитектор). Исследовательская деятельность старшеклассников («попытка объять необъятное») Итак, вернемся к вопросу о качестве образования и необходимости его повышения. Позволю себе еще раз процитировать Концепцию модернизации российского образования до 2010 года. Предполагается, что у выпускников будет сформирован «…опыт самостоятельной деятельности и личной ответственности обучающихся, т. е. ключевые компетенции, определяющие современное качество содержания образования». То есть современный молодой человек должен сегодня не столько уметь что-то делать и знать, сколько уметь учиться делать, уметь применять знание. У старшеклассника должны формироваться навыки самостоятельного исследования! В рамках урока эту задачу полностью не решить. Поэтому я, как и многие мои коллеги, занимаюсь со своими учениками исследовательской работой внеурочно. Прежде всего, это подготовка работ и их защита на ученических научно-практических конференциях различного уровня. О том, как протекает эта работа, о ее проблемах и удачных моментах, я хочу рассказать далее. 1. Выбор темы. С чего начинается любое исследование? Конечно, с постановки задачи и создания проблемной ситуации. Очень часто – с детского вопроса. Я, как учитель, выступаю в этом случае в роли провокатора, побуждающего эти вопросы задавать. Я намеренно создаю в ходе урока ситуацию, при которой будет задан тот или иной вопрос. Например, такой: «Вы все время говорите о действительных корнях уравнения. А что, бывают еще какие–то?» Из этого вопроса родилась работа «Дуальные числа» (комплексные числа изучаются в программе профильной школы, а о дуальных числах мало говорят). Или еще: « А почему в уравнении, задающем функцию, переменная в таких интересных скобочках?» И появляется работа «Функция антье», над которой мы трудились два года. Тема работы должна быть такой, чтобы работа не была реферативной! Должна всегда существовать проблема, которую надо решить, вопрос, который надо осветить с разных сторон, проанализировать, сделать выводы! Приведу несколько примеров тем исследований, выполненных учениками.
2. Участники исследования. Наиболее часто в связи с проектированием и исследованием в образовательном процессе говорят о развитии коммуникации – об умении работать в группе, организовывать межличностное общение и т. д. Поэтому состав исследовательской группы и количество участников – очень важный вопрос. Для меня стало уже традиционным выполнять каждое исследование с парой учеников. Попытка расширить состав до четырех человек была неудачной. В то же время один учащийся в целом с работой справлялся, но… В паре возникает умение договариваться, взаимообучение («я уже все понял, сейчас я тебе объясню!»), взаимоконтроль («так, у тебя что получилось?!»), умение распределять роли при выступлении, а также очень важная возможность разделения ответственности! Некоторые пары так сработались, что очень удачно выполняют исследовательские работы по другим предметам – физике (учитель Жданова Н. Р.), биологии (учитель Стяжкина Е. И.). 3. Накопление материала и первичная обработка результатов. Выявление проблем. Еще один важный вопрос – источники информации. Конечно же, учащиеся имеют практически неограниченный доступ к интернет–ресурсам и электронным библиотекам, поэтому очень важно не допустить бездумного скачивания материала из интернета, как это иногда бывает. Любой плагиат недопустим, и учащиеся это прекрасно осознают. Тем более что несколько раз при проверке решений, приведенных в электронных источниках, мы находили в них ошибки! Поэтому все, что мы можем взять – это краткие теоретические сведения и примеры задач, приведенных без решения! Иначе всякое исследование, всякая самостоятельная деятельность теряет смысл. На этом этапе мы составляем план работы (точнее, это происходит после выбора темы), определяем ее объем, формулируем вопросы, на которые собираемся ответить. Затем знакомимся с теоретическим материалом и пробуем самостоятельно решать задачи. Идет процесс усвоения нового знания. Абсолютно самостоятельный. В ходе этой работы постоянно возникают вопросы, отвечать на которые приходится вместе. Это очень кропотливый процесс, но он необходим, потому что пока мы не выйдем на уровень свободного владения материалом, двигаться дальше нельзя. 4. Окончательная обработка результатов. Написание доклада. Создание презентации. При окончательной обработке результатов очень важно показать учащимся, что исследование можно продолжать дальше, что после ответов на поставленные вопросы возникают новые. Например, в работе «Решение функциональных уравнений методом подстановки» возникла проблема: уравнение  (естественно, данное специально!) указанным методом не решается! Тогда почему были решены все предыдущие? В чем отличие от них последнего? В чем сходство всех остальных? Идет выход на элементы теории групп! Тема будущего исследования…Конечно, опыт отбора материала для доклада, для презентации, приходит не сам по себе. Этому тоже приходится учить. И если работы восьмиклассников написаны почти под диктовку, то работы десятиклассников – самостоятельны на 95%. Единственное, что приходится делать самой – писать тезисы. Ученики просто отказываются сокращать свои доклады под нужный объем, так важно для них каждое слово! 5. Подготовка к выступлению. Выступление. Подготовка к выступлению начинается с просмотра и редактирования готовых презентаций всеми участниками рабочей группы. Обращаем внимание на дизайн презентаций, отсутствие ошибок, доступность и лаконичность высказываний, установленный регламент, умение «держать» аудиторию. Ведь нужно не только рассказать о своей работе, но и сделать ее понятной для непосвященных! Поэтому вопросы, зачастую очень острые, задают все. Учимся защищаться! Это тоже приходит не сразу. Но наши будущие студенты, аспиранты и научные работники, да и просто менеджеры, учителя, предприниматели, учатся держаться перед аудиторией, «держать удар», «сохранять лицо» при неудаче. Я хотела бы обратить внимание на то, как современное положение о проведении научно-практических конференций осложнило работу учителя и сузило возможности развития этих навыков у учащихся. Ведь у нас осталась возможность выступить только на ОДНОЙ муниципальной и ОДНОЙ региональной конференции. А если работа нуждается в «доводке», или ученик просто растерялся перед аудиторией? Получается, что работа на второй год уже никуда не будет допущена? Можно не работать? А научные работники могут всю жизнь посвятить одной теме… Между тем работа учениц гимназии №87 Дроздовой Светланы и Куликовой Анастасии «Функция антье» (приложение 2), прежде чем стать победителем региональной конференции «Инициатива молодых» в 2009 году, создавалась два года и была представлена на других конференциях трижды! Дело не в самой победе, а опыте выступлений, который девочки получили! Теперь такой возможности нет. Заключение Итак, в чем же влияние внедрения исследовательской технологии в образовательную деятельность на качество образования? Ведь «если звезды зажигают, значит, это кому-нибудь нужно»? Если рассматривать повышение качества просто как улучшение оценок, то, наверное, никакого влияния нет. Более того, серьезно увлеченные исследованием ученики иногда просто пренебрегают «неважными» для них предметами. Но если поставить вопрос шире, и под повышением качества понимать расширение возможностей ученика, развитие принципиально новых для него навыков (например, коммуникативной компетентности), самостоятельности суждений, появления новых знаний, то, видимо, исследовательская деятельность приобретает особую важность. Учитель, увлеченный исследованиями и вовлекающий в это интереснейшее дело своих учеников, решает очень важную задачу – воспитание будущего активного члена общества. Умение критически мыслить, анализировать информацию, иметь активную позицию, отстаивать свою точку зрения – это навыки, необходимые современному человеку. Литература
6. К. Н. Поливанова, «Проектная деятельность школьников» - М., «Просвещение», 2008 г. 7. Н. В. Бурлак, «Элементы исследовательской технологии в преподавании математики», Сборник материалов IV Областной научно-методической конференции. – Саратов: ГОУ ДПО «СарИПКиПРО», 2009 г.,57 стр. Приложение 1 Лабораторная работа № 3. Тема: «Объем прямоугольного параллелепипеда» Цель: научиться изображать прямоугольный параллелепипед, вычислять объемы заданных фигур по их моделям. Оборудование: модели прямоугольных параллелепипедов, кубов, линейка, простой и цветные карандаши. ХОД РАБОТЫ.
(у каждого ученика модель прямоугольного параллелепипеда)
Приложение 2
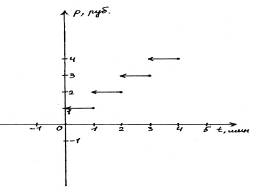
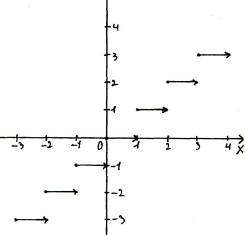
«Антье, свойства и график» Мы часто сталкиваемся с различными ситуациями, которые можно описать математическим языком и построить графики зависимости одной величины от другой. Рассмотрим несколько таких задач.
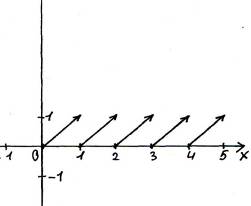
Если рассмотреть эти графики зависимостей, то можно увидеть, что они похожи друг на друга, то есть существует какая-то определенная функция, описывающая такие процессы. Это – функция антье (целая часть действительного числа). В различных математических олимпиадах последних лет присутствуют задачи, основанные на применении целой и дробной части действительного числа. В школьном курсе математики эти понятия не изучаются, и, поэтому многие школьники вообще не приступают к решению подобных задач. В своей работе мы ознакомились с понятием антье и дробной части действительного числа, научились решать некоторые уравнения, содержащие выражения под знаком антье графическим и аналитическим способами, а так- же строить графики функций . Понятие антье Целой частью действительного числа х называется наибольшее целое число, не превосходящее х. Обозначается целая часть х символом "[х]" и называется "антье" (от франц. entire- целый). Например: [2,3]=2, [-2,3]=-3, [2]=2, [-3]=-3. Наряду с целой частью числа существует понятие дробной части числа, которая обозначается "{х}" и определяется следующим образом: {х}=х - [х]. Очевидно, что для любого действительного числа х выполняется двойное неравенство: 0≤{х}<1. График функции у=[х] изображен на рисунке 3, а функции у={х} – на рисунке 4.
Решение уравнений, содержащих антье, графическим способом Приведем примеры уравнений, содержащих антье, которые можно решить графически. Для таких уравнений этот способ решения обладает рядом неоспоримых преимуществ. Пример 1. Решить уравнение х  -[х]=3.Решение: Преобразуем уравнение к виду х -3=[х] и построим в одной системе координат графики функций у= х-3 и у=[х] (графики функций изображены на рис. 6).Т. к. графики этих функций пересекаются в единственной точке, то наше уравнение тоже имеет единственный корень, причем это число больше 1, но меньше 2. 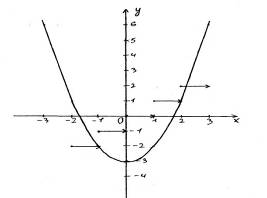 Если 2<х<3, то [х]=2. Тогда х -2=3, х=5, х=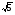 .Ответ: 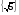 .Пример 2. Найти все числа х на отрезке [-2;2], которые удовлетворяют уравнению [х ]=[х].Решение: Уравнение [х ]=[х] можно решать аналитическим способом и функционально-графическим.I. Аналитический способ решения предложен в работе 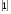 и состоит в следующем:Если х - целое число, то [х]=х, т. е. всякое целое число из отрезка [-2;2], а именно числа -2, -1, 0, 1, 2, будет решением уравнения. Пусть х - не целое число, т. е. х=[х]+α, 0≤α<1. Тогда х =[х]+α+2α[х]. Если [х]<0, то α+2α[х]= α(α+2[х])<0; следовательно, [х]<х<[х], т. Е. уравнение не имеет нецелых решений в этом случае.Осталось проверить два случая: [х]=0 и [х]=1. Если [х]=0, то х=α и [х ]=0, т. е. любое число из интервала (0;1) удовлетворяет уравнению. Если [х]=1, то х=1+α и х=1+2α+α. По условию [х]=[х]=1, а это возможно только при α+2α<1, т. е. 0<α< , следовательно, уравнению удовлетворяют все числа из промежутка [1;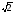 ). 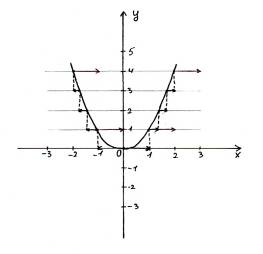Ответ: числа -2, -1, 0, 1, 2 и интервал (0; 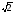).ІІ. Функционально-графический способ. Построим графики функций у=[х ] и у=[х] в одной системе координат и найдем абсциссы общих точек графиков. Очевидно, что такие точки либо имеют целые значения абсцисс (т. е. -2, -1, 0, 1, 2), либо принадлежат промежутку (0; 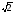).Ответ: все целые числа из промежутка [-2;2] и интервал (0; 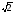).Заключение В данной работе мы рассмотрели определение, свойства и примеры применения новой для нас функции – антье, научились строить графики функций 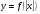 ,  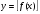. Эта работа посвящена, в основном, графическому способу решения уравнений, содержащих переменную под знаком антье. Однако применение этой функции этим не исчерпывается. В будущем мы планируем научиться решать уравнения аналитически, рассмотреть применение антье для решения задач на делимость и геометрических задач, а также практическое применение этой функции (экономические задачи, статистика). |
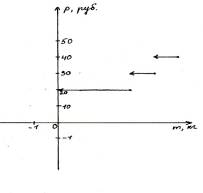Задача 1. 
