Научно-исследовательская работа по математике Подготовил: Раззамазов Никита Иванович
 Скачать 183.76 Kb.
|
МБОУ «СОШ №78» Теория вероятностей Научно-исследовательская работа по математике Подготовил: Раззамазов Никита Иванович Научный руководитель: Щеглова Галина Игнатьевна, учитель математики г. Барнаул, 2015 Содержание 1. Введение ••••••••••••••••••••••••••••••••••••••••••••••••••••••••••••••••••••••••••••••••••••••••• 3 стр. 2. Основная часть •••••••••••••••••••••••••••••••••••••••••••••••••••••••••••••••••••••••••••••••• 4 стр. 2.1. Определение ••••••••••••••••••••••••••••••••••••••••••••••••••••••••••••••••••••••••••• 4 стр. 2.2. История ••••••••••••••••••••••••••••••••••••••••••••••••••••••••••••••••••••••••••••••••• 4 стр. 2.3. Суть этого раздела •••••••••••••••••••••••••••••••••••••••••••••••••••••••••••••••••• 5 стр. 2.4. Комбинаторика и формулы •••••••••••••••••••••••••••••••••••••••••••••••••••••• 6 стр. 2.5. Как подсчитать вероятность? •••••••••••••••••••••••••••••••••••••••••••••••••••• 9 стр. 2.6. Практическое применение •••••••••••••••••••••••••••••••••••••••••••••••••••••• 12 стр. 2.6.1. Страхование •••••••••••••••••••••••••••••••••••••••••••••••••••••••••••••••• 12 стр. 2.6.2. Пенсии •••••••••••••••••••••••••••••••••••••••••••••••••••••••••••••••••••••••• 13 стр. 2.7. Интересные факты ••••••••••••••••••••••••••••••••••••••••••••••••••••••••••••••••• 13 стр. 2.7.1. Парадокс Монти Холла ••••••••••••••••••••••••••••••••••••••••••••••••• 13 стр. 2.7.2. Парадокс о днях рождения •••••••••••••••••••••••••••••••••••••••••••• 14 стр. 3. Заключение ••••••••••••••••••••••••••••••••••••••••••••••••••••••••••••••••••••••••••••••••••• 15 стр. 4. Источники информации •••••••••••••••••••••••••••••••••••••••••••••••••••••••••••••••••• 16 стр. ВВЕДЕНИЕ Математикой я интересуюсь давно, в прошлом году начал коллекционировать книги серии De Agostini. Одной из полюбившихся тем, о которой я узнал по этим книгам, стала теория вероятностей. Я решил исследовать её, перед собой поставил цель, задачи и выявил проблемы. Цель работы: донести до слушателя основные сведения об этой теории, показать, как правильно производить расчёты, как нужно рассуждать при решении задачи. Задачи работы: рассказать о принципах теории, формулах вычисления вероятностей, интересных фактах и практическом применении. Проблемные вопросы:
Актуальность исследования состоит в том, что теория вероятностей имеет практическое применение, в некоторых случаях может встретиться в обыденных ситуациях, таких как участие в лотерее, розыгрыш призов и пр. Объект исследования: теория вероятностей как раздел математики. Методы исследования: просмотр сайтов в Интернете, чтение книги, применение собственных знаний, полученных ранее. ОСНОВНАЯ ЧАСТЬ Определение Теория вероятностей – один из разделов математики, изучающий закономерности случайных явлений: случайные события, случайные величины, их свойства и операции над ними. История Возникновение теории вероятностей как науки относят к средним векам и первым попыткам математического анализа азартных игр, таких как кости, рулетка и др. Исследуя прогнозирование выигрыша в азартных играх, Блез Паскаль и Пьер Ферма открыли первые вероятностные закономерности, возникающие при бросании костей. Под влиянием поднятых и рассматриваемых ими вопросов решением тех же задач занимался и Христиан Гюйгенс. При этом с перепиской Паскаля и Ферма он знаком не был, поэтому методику решения изобрёл самостоятельно. Также важный вклад в развитие теории вероятностей внесли Якоб Бернулли, Пьер-Симон Лаплас, Симеон Пуассон и некоторые другие. В результате теория вероятностей приобрела строгий математический вид и окончательно стала восприниматься как один из разделов математики.    Якоб Бернулли Пьер-Симон Лаплас Симеон Пуассон 27 декабря 1654 - 16 августа 1705 23 марта 1749 — 5 марта 1827 21 июня 1781, — 25 апреля 1840 Суть этого раздела математики Теория вероятностей в общем виде показывает, каковы шансы определенного случая (на математическом языке такие случаи называются благоприятными исходами). Например, у нас есть монета с орлом и решкой. Какова вероятность того, что, подкинув монету, выпадет орёл? Очевидно, что ½. А какова вероятность того, что выпадет решка? Опять же, ½. Как видим, шансы выпадения орла и решки равны. В таком случае говорят, что события равновероятны. В общем виде равновероятными событиями называются такие события, которые могут случиться с одинаковой вероятностью. Вот еще пример: игральная кость. Если она является правильной фигурой, и её грани отличаются лишь количеством очков, то вероятность выпадения любого числа равна 1/6. Я провёл эксперимент. С помощью Интернет-программы (ссылка на сайт будет в разделе «Источники информации») смоделировал бросок монеты сначала 10, потом 100, и, наконец, 1000 раз.  Результаты представлены в таблице:
Как мы знаем, ½ = 50%. Из таблицы видно, что с бОльшим числом бросков отношение выпавших решек и орлов к общему количеству бросков стремится к 50%, то есть к ½. Из этого эксперимента можно сделать несколько выводов: во-первых, в некоторых случаях, когда это возможно, наши предположения о вероятностях можно проверить практическим путём. Во-вторых, с увеличением количества проводимых опытов вероятность становится очень близкой к вычисленной. Последний вывод лежит в основе закона больших чисел. В «идеале» вычисленная вероятность и практическая должны быть равны, но быть уверенным полностью в этом можно тогда, когда опыт будет проводиться бесконечное число раз, что в реальной жизни невозможно. Поэтому, вычисленную вероятность можно назвать как бы «эталоном», к которому стремятся результаты подобных экспериментов. Комбинаторика и формулы Определение комбинаторики как раздела математики довольно трудное для понимания, поэтому приведу несколько примеров, чтобы стало понятно, чем же она занимается. Также разберём некоторые формулы, которые помогут нам в дальнейшем. Пример 1. У нас есть 2 книги, назовём их А и В. Сколько существует способов их размещения по порядку вертикально на пустой полке? Очевидно, можно поставить сначала А, потом В. Или же сначала В, потом А. А еще как-то можно? Нет, больше никак. Значит, существует 2 способа их размещения. Идём дальше. П 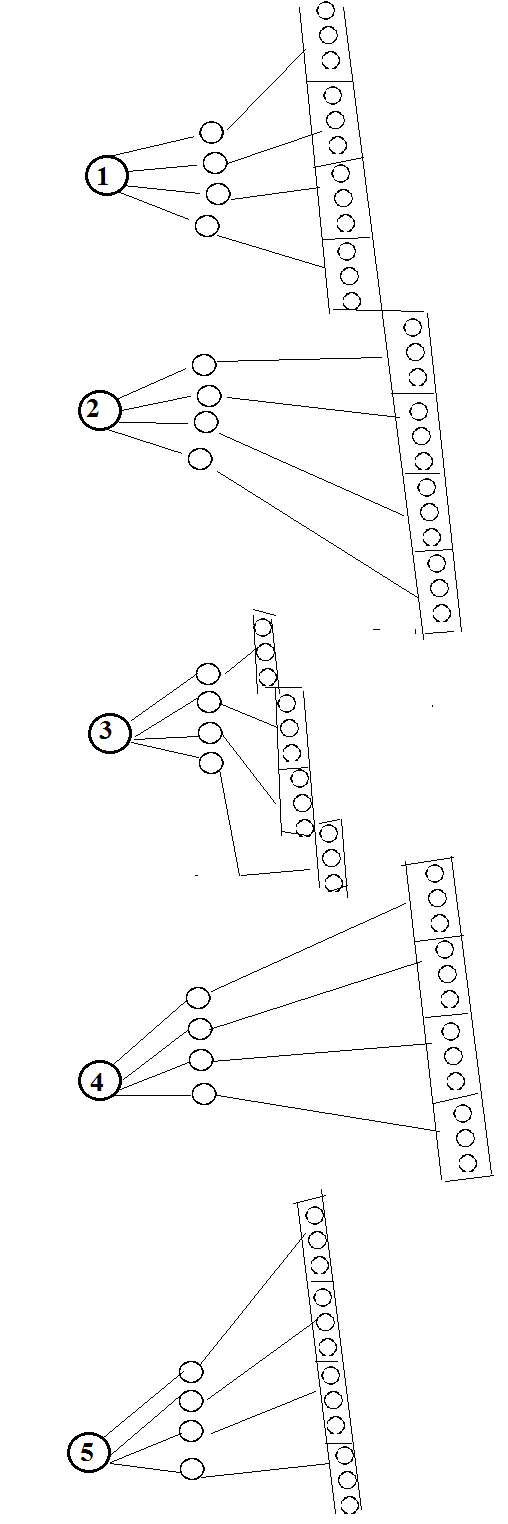 ример 2. У нас есть уже не 2, а три книги, А, В, и С. Сколько же здесь существует способов размещения таким же образом? Чувствуется, что уже посчитать будет немного труднее, но здесь еще можно перебрать разные варианты. Получим число 6. Но математика все-таки точная наука, нужно как-то посчитать «по-правильному». Да и не всегда можно таким интуитивным способом посчитать: либо долго, либо трудно, или же вообще и то, и другое. Нужны какие-то формулы, которые бы помогали нам вести подсчёт проще и быстрее. Но об этом чуть позже.Пример 3. В забеге участвуют 5 спортсменов. Сколько существует вариантов первых пришедших к финишу троек? Будем считать, что никакие 2 и более участников не пришли одновременно, и все дошли до финиша. В Схема 1 данном случае для нас важен не столько САМ ответ, сколько понимание решения задачи. Этот способ рассуждения применим и к прошлым задачам. Итак, 1 место может получить любой из 5 участников. 2 место – любой из оставшихся 4 (ведь не может один и тот же человек занять несколько мест!). 3 место – любой из оставшихся 3. И вот здесь нужно применить формулу. Но прежде нужно понять, почему мы применяем именно её, а не другую. Сделаем схематический рисунок, называемый «деревом». П  осчитав количество кружков в последнем столбце, получим число 60. Вроде бы и нашли метод нахождения числа возможных вариантов, но этим методом трудно решить задачи с большими числами. Если мы возьмём 10 участников, и попробуем найти возможные пятёрки лучших, нам потребуется нарисовать такое дерево, которое либо займёт много места, либо, если рисовать на обычном листочке, будет маленькое в размерах, можно будет запутаться. Да и считать придётся много в последнем столбце (всего-то 30240 «кружков», т.е. вариантов, получится!). Итак, формула для подсчета вариантов такова:А = n1*n2*…*nk Где А – искомое число благоприятных исходов; n1, n2, nk – количество возможных отдельных событий (под каждым множителем стоит отдельное событие). По формуле получаем: А (троек первых мест) = 5*4*3 = 60 В приведённых выше примерах порядок участников на пьедестале имел значение. Нам было важно, кто будет первым, вторым и третьим. Однако существуют ситуации, когда порядок выбора не важен, и на эти ситуации тоже есть своя формула. Снова для начала рассмотрим пример, затем – формулу.  Пример 4. В классе 15 учеников. Один из них, Петя, имеет 10 одинаковых наклеек. Однажды он решил подарить по одной наклейке 10 своим одноклассникам. Сколько существует способов распределения наклеек между детьми? Может показаться, что достаточно найти кол-во человек, которые могут получить наклейки (их 14, Петя сам себе не подарит наклейку), и найти количество способов по уже известной формуле: 14*13*12*11*10*9*8*7*6*5 = 3 632 428 800. Но нет! Способов гораздо меньше. Сравним задачу о бегунах с этой задачей. В первом случае нам был важен ПОРЯДОК финиширования людей (говоря математическим языком, размещения людей по местам). Здесь же нет разницы, кто получит первую наклейку, кто получит вторую и т.д. Значит, способов должно быть меньше, так как в эти 3 с лишним миллиарда входят и те случаи, в которых люди, получившие наклейки, те же самые, отличие между этими случаями только в порядке получения. Если сократить это число, получим правильный ответ. Но как же это сделать? Достаточно посчитать, сколько существует «порядков» из 10 человек, которые получат наклейки (что мы уже умеем делать). После этого разделить на это произведение число, получившееся у нас в результате «неверного» решения, а именно 3 632 428 800. Тем самым мы избавимся от одинаковых «десятков» людей. Получаем следующее выражение: 14*13*12*…*5 / 10*9*8*…*1 Сократим числитель и знаменатель, получим 14*13*12*11 / 4*3*2*1 Продолжим преобразование: 7*13*11 = 1001 Как видим, число получилось намного меньше того, которое мы рассчитали вначале. Поэтому, следует различать случаи в комбинаторике, которые называются РАЗМЕЩЕНИЯМИ и СОЧЕТАНИЯМИ. Размещение требует учёта порядка каких-либо предметов (под этим словом будем понимать элементы множества, множество же – совокупность каких-либо предметов, объединённых общим свойством); сочетание не требует порядка. Как видно из прошлого примера, это очень важно понимать. А чтобы выяснить, какой из этих случаев содержится в задаче, нужно просто немного подумать, логически поразмышлять: нужно ли учитывать порядок или нет? А теперь перейдём к формуле. Приводить ещё один пример не стану, остановимся на этом. В общем виде выражение выглядит так: 14*13*12*…*5 / 10*9*8*…*1 В некоторых случаях удобно использовать факториал – произведение всех натуральных чисел от 1 до n включительно. Записывается факториал с помощью значка восклицательного знака (!). Например, факториал числа 4 пишется так: 4!. Применим это и к нашему выражению: 14*…*5/10! Если мы посчитаем количество множителей в числителе, то увидим, что это число равно числу, записанному в знаменателе, если мы уберём значок факториала. Это и логично: ведь в знаменателе мы и написали произведение всех чисел от 10 до 1, так как это число показывало количество способов размещения наклеек среди 10 человек (не среди класса, а в уже как бы отобранной «десятке»!). Запишем общую формулу нахождения количества способов: С = А / N!, где А – количество исходов ситуации с учётом порядка, N – количество множителей в числителе, т.е. множителей, образующих произведение А. Итак, чем же занимается комбинаторика? Комбинаторика занимается вычислением (нахождением) возможных исходов события. Это может помочь находить вероятности каких-либо исходов. Как подсчитать вероятность? Для того чтобы найти вероятность какого-либо случая, нужно тоже применять некоторые формулы. Но для начала разберём свойства в теории вероятностей, принимаемые как аксиомы. 1) Любая вероятность, принадлежащая данному множеству, больше либо равна 0. 2) Вероятность достоверного события равна 1. 3) Для совокупности несовместных событий из множества исходов случайного эксперимента справедливо следующее равенство: P (S1 или S2 или … или Sn …) = P (S1) + P (S2) + … + P (Sn), где P (Sk) – вероятность какого-либо события, S1, S2, Sn – события какого-либо эксперимента. Разберём эти аксиомы. Первая гласит о том, что любая вероятность события либо равна 0, то есть событие невозможно, либо больше 0, т.е. событие может случиться. Вторая говорит о том, что событие, которое произойдёт в абсолютно всех экспериментах, имеет вероятность, равную 1. Третья аксиома о том, что вероятность некоторых несовместных событий (т.е. тех, которые не могут случиться в одних и тех же экспериментах одновременно) можно определить как сумму отдельных вероятностей этих событий. Например, вероятность того, что, подбросив игральный кубик, выпадет либо 1 очко, либо 2 очка, равна сумме отдельных вероятностей этих исходов: P (1 или 2 очка) = P (1 очко) + P (2 очка) = 1/6 + 1/6 = 1/3 Исходя из этих аксиом, можно найти и другие важные свойства: 1) Вероятность какого-либо события равна 1 минус вероятность противоположного ему события: P (Sa) = 1 - P (Sb), где Sa и Sb – противоположные события. 2) Вероятность любого события меньше либо равна 1, так как достоверное событие обладает наибольшей вероятностью по определению, а оно равно 1. 3) Вероятность невозможного события равна 0: P (  ) = 0,где - невозможное событие.4) Для двух произвольных событий определённого множества исходов какого-либо эксперимента справедливо следующее равенство: P (S1∪S2) = P (S1) + P (S2) - P (S1 ⋂ S2), где S1 и S2 – произвольные события, P (S1∪S2) – вероятность того, что произойдёт либо S1, либо S2, P (S1 ⋂ S2) – вероятность того, что эти два события произойдут одновременно. Теперь, зная аксиомы и свойства событий и вероятностей, перейдём к рассмотрению примеров и формул, с помощью которых мы будем находить искомые вероятности. П 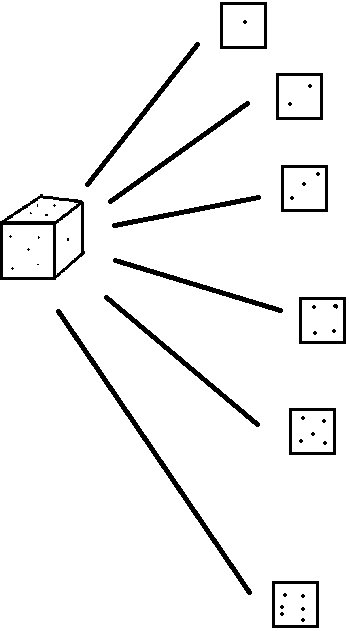 ример 1. Снова возьмём игральный кубик. Вероятность того, что выпадет 1 очко (равно как и 2 или 3 или 4 и т.д.), равна 1/6. Как мы нашли это число? Разделили число благоприятных исходов (а именно 1) на число всех возможных исходов (их 6). Чтобы понять, почему производились такие расчёты, давайте снова нарисуем чертёж. Мы знаем, что все исходы броска кубика равновероятны. Помним, что вероятность достоверного события равна 1. Получается, нахождение вероятности сводится к решению уравнения: 6х=1, где х – искомая вероятность. Отсюда х = 1/6. Чтобы не прибегать к составлению уравнения и решению его, выведем формулу для подсчёта вероятности: P = n/m, где n – число благоприятных исходов m – число всех возможных исходов. К Схема 2 ак видим, нам нужно найти вероятность выпадения ОДНОЙ из ВСЕХ сторон, т.е. число благоприятных исходов равно 1, всех возможных – 6 (так как сторон в кубике 6). Отсюда получаем ту же самую вероятность, 1/6. Пример 2. Найдём вероятность того, что в кубике выпадет ЛИБО 1 очко, ЛИБО 2 (вместо этих очков можно брать и другие числа, это не имеет значения в данном случае). В этом примере благоприятными будут исходы выпадения и 1 очка, и 2, так как нам нужно, чтобы выпало хотя бы одно из этих значений. Зная формулу, рассчитаем вероятность: P = 2/6 = 1/3. Но можно рассчитать и по-другому. Вспомним 3 аксиому: «Для совокупности несовместных событий из множества исходов случайного эксперимента справедливо следующее равенство: P (S1 или S2 или … или Sn …) = P (S1) + P (S2) + … + P (Sn)» Несовместные события, как уже говорилось ранее, - те, которые НЕ могут происходить одновременно. Действительно, не могут выпасть 1 очко и 2 очка после одного броска (да и вообще любые две стороны). Значит, чтобы посчитать вероятность того же исхода (выпадет либо 1 очко, либо 2), нужно сложить вероятности ОТДЕЛЬНЫХ событий. Каждое из них имеет вероятность 1 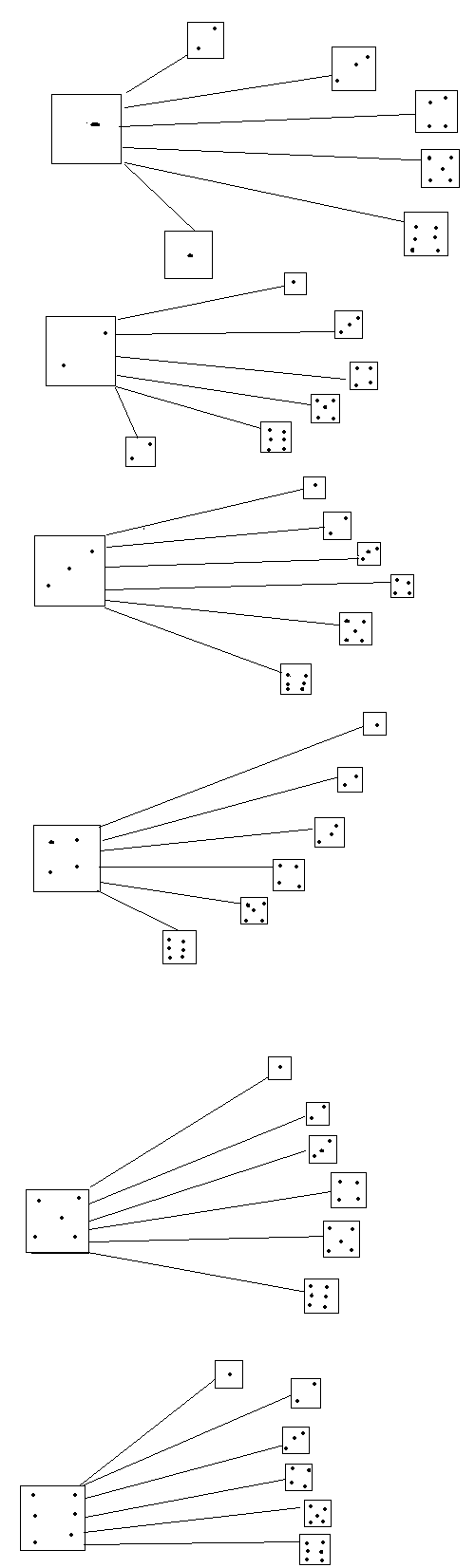 /6, как мы уже видели ранее. Значит, искомая вероятность равна: 1/6 + 1/6 = 1/3. Если мы захотим рассчитать вероятность для выпадения либо 1, либо 2, либо 3 очков, можем сделать это с помощью тех же формул: 1) 3/6 = 1/2 2) 1/6 + 1/6 + 1/6 = 1/2 Напомню, формулы из 3-ей аксиомы действует в том случае, если события НЕ могут произойти одновременно. П Схема 3 ример 3. Подбросим 2 игральных кубика, полностью одинаковых между собой. Какова вероятность того, что и у первого, и у второго выпадет по 1 очку? Будет грубой ошибкой сложить вероятности отдельных событий, так как они МОГУТ произойти одновременно (вероятность чего мы и ищем). Поэтому, здесь нужно найти другое решение. Обратимся к рисунку. В левом столбике изображены исходы броска 1-ого кубика, в правом – 2-ого. На каждую грань «приходится» по 6 исходов броска 2-ого кубика, т.е. если у нас выпадет, например, 4 очка, то на втором кубике может выпасть ЛЮБАЯ из 6 его сторон. Посчитав количество всех исходов этого эксперимента, получим число 36. Значит, общее число исходов равно 36. Благоприятных исходов – 1. Для нахождения вероятности нужно разделить 1 на 36: 1/36. Общее число исходов найдено тем способом, которым, как уже было сказано, неудобно считать. Проще найти произведение исходов броска 1-ого кубика и исходов броска 2-ого кубика, так как на каждый исход броска 1-ого кубика (а их 6) приходится 6 исходов броска 2-ого: 6*6 = 36. Как видим, запись «6*6» можно заменить «6^2» (^ - знак возведения в степень). Если мы возьмем не 2, а, к примеру, 4 кубика, то количество общих исходов равно 6^4 = 1296. Итак, в общем виде формула для нахождения вероятности исхода, зависящего от нескольких событий такова: P (S1 и S2 и … и Sn) = Р (S1) * Р (S2) * … * Р (Sn), где Р (S1 и S2 и … и Sn) – вероятность исхода, при котором происходят несколько событий одновременно, Р (S1), Р (S2), …, Р (Sn) – вероятность исходов отдельных событий, происходящих одновременно. Итак, мы разобрали основные формулы нахождения общего числа исходов и вероятностей. С их помощью можно решать различные задачи, не забывая при этом, в каком случае мы применяем тут или иную формулу. Практическое применение Страхование К  ак мы знаем, страховые компании выплачивают деньги застрахованному лицу, если произошёл какой-либо несчастный случай. Сумма, которую должен заплатить человек страховой компании и застраховать тем самым что-либо или кого-либо, рассчитывается определённым образом. Основой, на которую опираются страховые компании, является статистика - отрасль знаний, в которой излагаются общие вопросы сбора, измерения и анализа массовых статистических данных. Эти данные несут информацию о том, сколько за прошедшее время произошло несчастных случаев одного вида (например, аварий, ДТП и пр.), вероятность того, что они произойдут и некоторые другие сведения. Таким образом, для подсчёта стоимости страхового полиса и компенсации, выплачиваемой страховой компанией, требуются накопленные ранее знания о случившихся несчастных случаях, о теории вероятностей и т.д.Пенсии Г  раждане, проработавшие некоторое количество времени и получавшие так называемые «белые зарплаты», по наступлении пенсионного возраста получают пенсии – регулярные денежные пособия. Для того чтобы рассчитать пенсионный возраст, нужно учитывать такие статистические данные, как продолжительность жизни, ожидаемая продолжительность предстоящей жизни, некоторые другие показатели. Также применение теории вероятностей, статистики, различных таблиц используется, как я уже сказал, в медицине, в механике и инженерном деле. Например, таблицы смертности в медицине, срок полезного функционирования детали или механизма в механике, инженерии. Как видим, математика может пригодиться в вышеприведённых сферах государства, промышленности и т.д. Интересные факты Парадокс Монти Холла  Вы попали в финал телевизионного конкурса, и перед вами – три закрытые двери. За одной из них – главный приз, автомобиль, за двумя другими – козы. Нужно выбрать одну из трёх дверей. Когда вы указали на одну из дверей, ведущий должен открыть одну из оставшихся дверей, за которой находится коза. Он даёт вам шанс изменить выбор. Вы можете воспользоваться этим, а можете оставить своё решение без изменения. Как нам поступить, чтобы увеличить шансы на выигрыш? Или же они не изменятся, и от нашего решения вероятность не зависит? Сперва покажется, что вероятность одинакова и равна ½. Рассуждения таковы: так как перед нами 2 закрытых дверей, и за одной из них находится приз, значит, мы можем с одинаковой вероятностью как выиграть, так и проиграть (не будем принимать козу за выигрыш). Но такой ход мыслей неверен. Рассуждения с математической точки зрения следующие: перед нами 3 двери, на каждую приходится вероятность выигрыша по 1/3. Когда мы выбираем дверь, ведущий показывает, за какой дверью приза нет. Значит, если он открыл именно эту дверь, то, скорее всего, приз находится за той, которую он не открыл. На эту невыбранную закрытую дверь приходится вероятность 2/3. Чтобы лучше понять эту ситуацию интуитивно, изменим количество дверей. Пусть их будет не 3, а 1000. Мы выбрали одну из них, вероятность победы – 1/1000. Ведущий убрал 998 дверей. Скорее всего, приз окажется за той дверью, которую он не открыл. Сначала была вероятность выигрыша 1/1000, теперь, изменив выбор, можно увеличить её на 998/1000. Я думаю, это число показывает, что выгоднее изменить выбор, нежели оставить. Напомню, он открывает только ту дверь или те двери, которые выбраны не были, и за которыми находятся коза или несколько коз. Для подтверждения этих рассуждений можно провести подобный опыт со своим напарником: взять, к примеру, 3 коробка от спичек, 2 монеты по 50 копеек и 1 монету в 1 рубль (можно взять и другие, лишь бы 2 были одинаковы, а 1 – либо больше, либо меньше). Один человек играет роль ведущего, другой – участника. Далее правила ясны: ведущий наугад располагает монеты под коробками, участник не знает, где какая монета. Игрок выбирает любой из них. Ведущий убирает тот коробок, под которым меньшая по достоинству монета, и который не был выбран игроком. Далее участник меняет свой выбор. Если он выиграл, на листок записать букву В, если проиграл – букву П. Желательно проводить этот опыт большое число раз (вспомните закон больших чисел: чем больше количество проводимых экспериментов, тем ближе практическая вероятность будет к теоретической). Лично я со своим папой однажды провёл его 50 раз. Получилось так, что выиграл 31 раз, а проиграл – 19. Не стоит забывать, что монеты желательно располагать в случайном порядке под коробками после проведения очередного опыта. Парадокс о днях рождения  В классе учатся 23 человека. Какова вероятность того, что хотя бы 2 ученика этого класса родились в один и тот же день? В очередной раз интуиция подсказывает, что вероятность крайне мала. Но на самом деле это не так. Давайте разберёмся. Примем, что число дней в году равно 365. Рассмотрим общую ситуацию для N человек, N не больше 365. Возьмём первого человека, он мог родиться в любой из 365 дней, равно как и второй, третий и т.д. до N. Следовательно, число всех возможных вариантов дней рождений равно 365^N. Из этих случаев найдём такие, в которых нет совпадающих дат рождения. В таких случаях первый человек мог родиться в любой из 365 дней, второй – в любой из 364, третий – в любой из 363 и т.д. до N человека, отмечающего день рождения в любой из 365 – N + 1 дней. Получается, что число случаев с несовпадающими датами рождения равно 365 * 364 * 363 * … * (365 – N + 1) = 365! / (365 – N)! Напомню, что для нахождения вероятности нужно число благоприятных исходов разделить на число всех возможных исходов. Поэтому, вероятность того, что все ученики будут отмечать дни рождения в разные дни, равна  . Но нас интересует вероятность рождения как минимум 2 учеников в одинаковые дни. Так как найденная нами вероятность противоположна той, которую мы собираемся найти, то нам нужно из 1 вычесть это выражение, подставить вместо N число 23 и произвести расчёты.  Получим следующее: При N = 23 вероятность равна 0,507, т.е. 50,7 %. Именно при этом значении вероятность больше 1/2. При N = 30 она становится больше 70 %, а при N = 45 она примерно равна 94 %. Не так уж всё и очевидно на первый взгляд! ЗАКЛЮЧЕНИЕ Теория вероятностей – довольно интересный, хотя в некоторых случаях и непростой для понимания, раздел математики. Он связан со многими важными для общества отраслями: медициной, страхованием, статистикой и др. Для понимания теории вероятностей нужно владеть азами некоторых других разделов математики, таких как комбинаторика, теория множеств. ИСТОЧНИКИ ИНФОРМАЦИИ
|