Мастер класс «Требования к современному уроку математики в условиях внедрения стандартов второго поколения»
 Скачать 285.98 Kb. Скачать 285.98 Kb.
|
    МБОУ «Тугустемирская средняя общеобразовательная школа» МБОУ «Тугустемирская средняя общеобразовательная школа»Мастер класс «Требования к современному уроку математики в условиях внедрения стандартов второго поколения» Учителя математики I квалификационной Категории Хайбрахмановой Г.Ф. 2012г Слайд 1 28k + 30n + 31m = 365 Эмблема занятия: Говорят уравнение вызывает сомнение, но итогом сомнения может быть озарение! Задание для коллег. Найти хотя бы одно решение уравнения. В конце занятия мы к нему вернёмся.
…Однажды ученики греческого философа Зенона обратились к нему с вопросом: «Учитель! Ты, обладающий знаниями во много раз большими, чем мы, всегда сомневаешься в правильности ответов на вопросы, которые нам кажутся очевидными, ясными. Почему?» Начертив посохом на песке два круга, большой и малый, старец молвил: « Площадь большого круга – это познанное мною, а площадь малого круга - это познанное вами. Как видите, знаний у меня действительно больше, чем у вас. Но все, что вне кругов, - это не познанное ни мной, ни вами. Согласитесь, что длина большой окружности больше длины малой, а следовательно, и граница моих знаний с непознанным большая, чем у вас. Вот почему у меня больше сомнений». Слайд 2 СФЕРАНЕПОЗНАННОГО ЗНАНИЯМУДРЕЦА Знания учеников Задумываемся ли мы над тем, какой он, путь совершенствования знаний, мышления, путь обогащения духовного мира? Как помочь ученику интересно и плодотворно пройти по этому пути? А для этого я предлагаю вам по-иному посмотреть на современный урок. II Предисловие Меняются цели Слайд 3 и содержание образования, появляются новые средства и технологии обучения, но какие бы не свершались реформы, урок остается вечной и главной формой обучения. Какие бы новации не вводились, только на уроке, как сотни и тысячи лет назад, встречаются участники образовательного процесса: учитель и ученик. Слайд 4 Между ними (всегда) – океан знаний и рифы противоречий. И это – нормально. Любой океан противоречит, препятствует, но преодолевающих его – одаривает постоянно меняющимися пейзажами, неохватностью горизонта, скрытной жизнью своих глубин, долгожданным и неожиданно вырастающим берегом. Что бы ни твердили о компьютеризации и дистанционном образовании, учитель всегда будет капитаном в этом плавании и главным штурманом проводки через все рифы. Как бы ни старались уравнивать учителя с учениками, он как был, так и остается главным действующим лицом на любом уроке. Только со временем меняются его роль и позиция. III Мастер-класс Слайд 5 Каждый урок должен быть для наставника задачей, которую он должен выполнять, обдумывая это заранее: на каждом уроке он должен чего-нибудь достигнуть, сделать шаг дальше и заставить весь класс сделать этот шаг. К. Д. Ушинский Принципиальным отличием современного подхода к урокам является ориентация на результаты освоения основных образовательных программ. Под результатами понимаются не только предметные знания, но и умение применять эти знания в практической деятельности. И сегодня я приглашаю вас вместе поразмышлять над вопросом В чем же новизна современного урока математики в условиях введения стандарта второго поколения? Слайд 6 Что такое стандарты нового поколения: это стихийное бедствие или всё таки мечта, осуществление которой, даёт простор для полёта мысли учителя и ученика. Давайте вместе сейчас попробуем сформулировать требования к современному уроку, отвечающие запросам новых стандартов (групповая работа) Я предлагаю вам карточки, из которых вы выберете те утверждения, которые, на ваш взгляд, являются обязательными требованиями к современному уроку. (3 комплекта карточек) Какие требования предъявляются к современному уроку:
(заготовка «Требования к современному уроку, в соответствии со стандартами второго поколения») Я предлагаю вам наклеить выбранные и одобренные коллегами утверждения на заготовленный лист, карточки помощницы, которой вы можете пользоваться при построении уроков в своей работе. (Диалог с залом во время работы группы.) Слайд 7 ? что бы вы хотели взять с традиционного урока в современный урок? ? от чего вы хотели бы навсегда отказаться? Как проходил обычный урок? Учитель вызывает ученика, который должен рассказать домашнее задание – параграф, прочитанный по учебнику. Затем ставит оценку, спрашивает следующего. Вторая часть урока – учитель рассказывает следующую тему и задает домашнее задание. Теперь же, в соответствии с новыми стандартами, нужно, прежде всего, усилить мотивацию ребенка к познанию окружающего мира, продемонстрировать ему, что школьные занятия – это не получение отвлеченных от жизни знаний, а наоборот – необходимая подготовка к жизни, её узнавание, поиск полезной информации и навыки ее применения в реальной жизни. Если говорить о конкретных методиках, обучающих универсальным учебным действиям, они могут включать в себя и экскурсии, и поиск дополнительного материала на заданную тему, и обмен мнениями, и выявление спорных вопросов, и построение системы доказательств, и выступление перед аудиторией, и обсуждение в группах, и многое другое. Уроки должны строиться по совершенно иной схеме. Если сейчас больше всего распространен объяснительно-иллюстративный метод работы, когда учитель, стоя перед классом, объясняет тему, а потом проводит выборочный опрос, то в соответствии с изменениями упор должен делаться на взаимодействие учащихся и учителя, а также взаимодействие самих учеников. Ученик должен стать живым участником образовательного процесса. На сегодняшний день некоторые дети так и остаются незамеченными в течение урока. Хорошо, если они действительно что-то услышали и поняли во время занятия. А если нет? Групповая форма работы имеет множество плюсов: ребенок за урок может побывать в роли руководителя или консультанта группы. Меняющийся состав групп обеспечит гораздо более тесное общение одноклассников. Мало того, практика показывает, что дети в общении раскрепощаются, ведь не каждый ребенок может легко встать перед всем классом и отвечать учителю. «Высший пилотаж» в проведении урока и идеальное воплощение новых стандартов на практике – это урок, на котором учитель, лишь направляя детей, дает рекомендации в течение урока. Поэтому дети ощущают, что ведут урок сами. Слайд 8 - 9 Отчёт групп А теперь я предлагаю вам попробовать выстроить урок в соответствии с этими требованиями.
Слайд 10 Например: Учитель: Давайте вместе определим каково будет начало нашего урока. I. Определение темы и цели урока Слайд 11
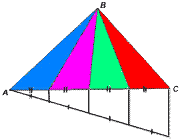
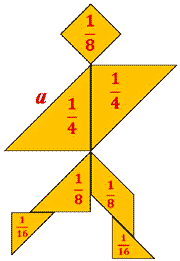
Как вы определили, что подойдёт именно второй ковёр? А теперь представьте, что комната может иметь и другую форму, например такую: (форма птицы) Слайд 12 А как в этом случае поступить? Как вы думаете, какова тема и цель сегодняшнего урока? (учащиеся формулируют цель урока.) Тема нашего урока - Вычисление площадей различных фигур Слайд 13 Цели урока: Тема урока: «Вычисление площадей различных фигур. Равновеликие фигуры» А ещё я добавлю вот такое понятие – Равновеликие фигуры. (Я бы спросила детей) Знакомы ли вам данные фигуры? Как вы считаете, какие фигуры могли бы называться равновеликими? ( Записать на доске всё что говорят дети) В конце урока мы выясним, кто из вас был прав. Я не случайно форму нашей воображаемой комнаты представила так. Что она вам напоминает? Это птица мудрости и если мы сегодня с ней справимся, то мы сумеем преодолеть одну из самых главных ступень науки геометрии. Знаете ли вы, что зарождение геометрических знаний, связанных с измерением площадей, теряется в глубине тысячелетий. Еще 4—5 тыс. лет назад вавилоняне вычисляли площади земельных участков, имеющих форму прямоугольника и трапеции, в квадратных единицах. Единицей измерения площади издревле использовали квадрат, так как именно квадрат обладает замечательными свойствами: равные стороны, равные и прямые углы; квадрат имеет ось и центр симметрии и совершенство формы. Квадраты легко строить, и ими можно покрыть без просветов фигуры любой формы. II. Формирование новых понятий и способов действий
III. Применение знаний, формирование умений и навыков Слайд 16
IV. Первичный контроль за усвоением знаний и умений Слайд 18
Пока группы работают, я предлагаю вам некоторые приёмы из методической копилки по созданию проблемных ситуаций на уроке математики. Слайд 19 I Создание проблемных ситуаций через умышленно допущенные учителем ошибки. В понимании детей учитель – это компьютер, который не может ошибиться никогда, и они обычно слепо копируют его решение. Пример №1.7 кл. Тема «Линейные уравнения с одной переменной». Решаю быстро уравнение: (3Х + 7) х 2 – 3 = 17 6Х + 14 – 3 = 17 6Х = 17 – 14 – 3 6Х = 0 Х = 0 Естественно при проверке ответ не сходится Проблемная ситуация. Ищут ошибку. Дети решают проблему. После этого учащиеся очень внимательно следят за мыслью и решением учителя. Результат - внимательность и заинтересованность на уроке. Пример №2. Даю задачу на дом и говорю: “У меня не получается”. Попробуйте вы, обращайтесь к кому хотите за помощью. Хотя задача решается. Проблемная ситуация. На другой урок у них радостные лица – они решили. Вот такие примеры активизируют деятельность учащихся.
Пример №3. 7 кл. Тема: «Линейная функция» Обычная форма задания: функция задана формулой У = Х + 5 найдите значение функции при Х = 0, 7, -5, 1. Занимательная форма задания: Приглашаю к доске ученика, даю ему карточку, на которой написано У = Х + 5. На доске заготовлена таблица:
Ученик из класса называет какое-нибудь значение Х. Ученик у доски вписывает это число в таблицу и, поставив его в формулу, находит и вписывает в таблицу соответствующее ему значение У. Затем другой ученик из класса называет другое значение Х и ученик у доски проделывает те же операции. Задача класса – “угадать” формулу, записанную на карточке. Проблемная ситуация создана. Выигрывает тот ученик, который первый назовет формулу. Пример №4.7 кл. Тема: «Формулы сокращённого умножения» Преступники украли в банке большую сумму денег. Их поймали, но похищенную сумму установить не удалось. Преступники категорически отказываются назвать её, утверждая, что записали это число в виде степени и зашифровали не только основание, но и её показатель. Экспертам удалось узнать основание степени. Это число 597. Но каким был показатель не говорят. После очередного допроса преступники сказали, что показатель степени является корнем уравнения ( 2y +1)2 – 4y2 =9 y = 2 5972 = (600 – 3)2 =6002 -2 х 600 х 3 + 32 = 360000 – 3600 + 9 =356409 Пример №5. 9 кл. Тема «Сумма n-первых членов арифметической прогрессии» Изучение вопроса о сумме n–первых членах арифметической прогрессии в 9-ом классе начинаю с рассказа: “Примерно 200 лет тому назад в одной из школ Германии на уроке математики учитель предложил ученикам найти сумму первых 100 натуральных чисел. Все принялись подряд складывать числа, а один ученик почти сразу же дал правильный ответ. Имя этого ученика Карл Фридрих Гаусс. В последствии он стал великим математиком. Как удалось Гауссу так быстро подсчитать эту сумму?” Проблемная ситуация: как найти быстро сумму первых 100 натуральных чисел? Решение проблемы (1 + 100) х 50 = 5050 Последовательность чисел 1, 2, 3,…,100 является арифметической прогрессией. Теперь выводим формулу суммы n-первых членов арифметической прогрессии.
Пример №6. 5 кл. Тема «Периметр прямоугольника» Семья Димы летом переехала в новый дом. Им отвели земельный участок прямоугольной формы. Папа решил поставить изгородь. Он попросил Диму сосчитать сколько потребуется штакетника, для изгороди, если на 1 погонный м. изгороди требуется 10 штук? Сколько денег потратит семья, если каждый десяток стоит 50 рублей. Проблемная ситуация: нужно найти длину изгороди (периметр прямоугольника). Пример №7. 5 кл. Тема: «Площадь прямоугольника» На прошлом уроке ребята мы измеряли длину и ширину нашего класса и по формуле, нашли его периметр. Р=( а+в)х2=(6+5)х2=22м. Помните! Посмотрите, пожалуйста, на пол. Краска сносилась, много чёрных полос. Вам нравится? Мне тоже не нравится. Я думаю, что летом нам нужно обязательно покрасить пол. Давайте с вами посчитаем, сколько денег нужно будет собрать с каждого родителя на покраску пола в классе, если 1 банка краски стоит 120 рублей и её хватает, чтобы покрасить 35 кв.м. Проблемная ситуация. Для решения этой задачи нам нужно найти площадь пола (площадь прямоугольника). Дорешав задачу до конца, получаем, что с каждого родителя придётся собрать по 40 рублей. А если в классе ещё что- то потребуется подкрасить, да ещё на ремонт школы?! Представляете, какие это деньги и как нам нужно беречь пол в классе и в школе. Пример №8. 5 кл. Тема «Проценты» Вы знаете, что в этом году нас награждили грантом губернатора. Конечно же, в этом и ваша заслуга. Спасибо. Размер премии 200 тыс. руб. Но мы получим не все деньги. Вычитают подоходный налог 13%. Я хочу, чтобы вы помогли сосчитать, какую сумму мы получим Вопрос: «А как же мы вам поможем, если мы не знаем, что такое процент?» Проблемная ситуация создана. Ребята с удовольствием работают в течении всего урока. В конце урока дорешивают задачу до конца. Я вижу радостные лица ребят. Они справились с проблемой!
Пример №9.5 кл. Тема «Площадь прямоугольника». На уроке технологии Серёжа выпиливал лобзиком и получил различные остатки фанеры. В каком из остатков выбрасывается фанеры больше? Проблемная ситуация. Нужно найти площадь данной фигуры. Вывод: разбить фигуру на прямоугольники, найти площадь каждой части и сложить (один из вариантов) Пример.№10. 5 кл. Тема «Площадь квадрата» К уроку вам было дано задание из газеты склеить 1 м2. Вы сделали это? Молодцы. Давайте посмотрим, сколько человек поместится на нём. Выясняем, что 4 человека. Как вы думаете, возможно ли на квадратной площадке со стороной 30 км. поместить всё население мира ?( 6,5 млрд.) Проблемная ситуация: нужно найти площадь площадки (площадь квадрата) Пример №11. 6 кл. Тема «Координатная плоскость» На этапе активного и осознанного усвоения нового материала, а также на этапе закрепления применяю практические работы «Животные на плоскости», «Астрономия и координатная плоскость». Ребята строят точки по координатам и рисуют животных и созвездия, затем рассказывают про них. Также выполняют творческие работы, сами предлагают свои рисунки и по ним составляют задания.
Пример№12 Третьекласснице Даше учительница дала задание сосчитать, сколько треугольников изображено на рисунке. Она нашла 5 треугольников. Подошла Лена и нашла 7 треугольников. Кто из них прав? Попробуем посчитать вместе. 2. Что общего в данных фигурах, а в чём различие?
Пример№13. 7 кл. Тема «Формулы сокращённого умножения» Вычисляем (2 х 5)²= 2² х5² = 100 (3 х 4)²= 3² х 4² = 9 х 16 = 144 (5 : 6)² = 5² : 6² = 25 : 36 (3 + 4)² = 3² + 4² = 9 + 16 = 25 Попробуйте сосчитать по-другому. ( 3 + 4)² =7² = 49 Проблемная ситуация создана. Почему разные результаты? ( 3 +4)² ≠ 3² + 4²
Пример14. 7 кл. Тема «Решение задач» На заправке села Всехсвятское две цистерны. В начале посевной обе цистерны заполнены. В 1 было 59 т бензина, а во 2 - 44 т. Через сколько дней в цистернах останется одинаковое количество горючего, если ежедневно из 1 цистерны ежедневно расходуется 5т, а из 2 - 2 т. Решают с помощью уравнения (алгебраический) 59 – 5х = 44 – 2х А вот вчера четвероклассник Стас, который не умеет решать такие уравнения, тоже смог её решить. Проблемная ситуация: какой способ он предложил (арифметический)
Пример №15. 5 кл. Тема «Длина окружности» Ещё древние греки находили длину окружности по формуле С=Пхд Д это диаметр окружности. Вопрос: а что же такое п? Работаем в парах, выполняя необходимые измерения. 1.Опоясать стакан ниткой, распрямить нитку, длина нитки примерно равна длине окружности стакана. Чтобы получить более точный результат, нужно это проделать несколько раз. Занесите данные в следующую таблицу.
2.Измерьте диаметр стакана линейкой. Данные занесите в таблицу. 3.Найдите значение П, как неизвестного множителя. Можно пользоваться калькулятором. 4.Каждой паре занести вычисленное значение П в таблицу на доске. Полученные значения П
П это бесконечная дробь, современные машины могут определить до миллиона знаков после запятой. П=3,1415926… Для того, чтобы легче запомнить цифры надо сосчитать количество букв в каждом слове высказывания: «это я знаю и помню прекрасно» В дальнейшей работе мы будем использовать значение П =3,14 Исследование проведено. На уроке кроме исследовательской работы удачно использовалась работа в парах. Сотрудничество и взаимопомощь принесли желаемый результат. Проблема решена. Имея успех в небольших исследованиях на уроках, некоторые ребята вовлекаются в более серьёзные исследования, требующие много времени. Это уникальная возможность для ученика сделать своё открытие, узнать то, что до него никто не знал. Исследования помогают расширить кругозор ученика, повысить самооценку, самоутвердиться, формировать исследовательскую компетентность. Рекомендации учителям по созданию проблемных ситуаций на уроке.(буклеты) 1.Подводить к противоречию с уже известным и предлагать самим находить способ разрешения. 2. Побуждать делать сравнения, обобщения, выводы. 3. Создавать ситуации включения, используя задания, связанные с их жизненным опытом. 4. Использовать задачи с заведомо допущенными ошибками. 5. Предлагать практические исследовательские задания. 6. Отыскивать различные способы решения одной и той же задачи. 7. Излагать различные точки зрения на один и тот же вопрос. 8. Учить составлять задачи по статистическим данным своего населённого пункта. 9.Использовать тесты с выбором правильного ответа. Отчёт групп: Слайд 19 - 20 Рефлексия: Группы прекрасно справились с заданием: мне хочется вас спросить. Что вызвало у вас наибольшее затруднение? С чем вы справились легко? Какие чувства испытывали вы, работая сообща в команде? Площади каких фигур вы теперь уже умеете вычислять? А дома вычислите площадь птицы. Вернемся к началу занятия. 28k + 30n + 31m = 365 Кто увидел? Кто догадался? Кто решил? “Смотреть – не значит видеть!” Ответ: 365 – это количество дней в году, 28 – количество дней в феврале, 30 – количество дней имеют 4 месяца в году, 31 – количество дней имеют 7 месяцев в году. Тогда: 28 ·1 + 30 · 4 + 31 · 7 = 365. Вывод: С помощью этого я хотела показать вам, что создание проблемных ситуаций на уроках математики не только формирует ту систему математических знаний, умений и навыков, которая предусмотрена программой, но и самым естественным образом развивает у школьников творческую активность. Слайд 21 Заключение: Если ребята встречаются с затруднениями в своей работе можно провести небольшое отступление с очень красивой историей. Эдисон, который изобрел лампочку, на самом деле он ее усовершенствовал – лампочка была изобретена до него. Но его на конференции один из журналистов спросил: «Вы провели 2000 экспериментов пока не получили свою лампочку. Такое большое количество неудач, как вы к этому относитесь?» Он сказал, что это не были неудачи – это было 2000 удачных способов не получить свою лампочку». Поэтому ученикам надо понимать, отрицательным результатом будет неумение выдвигать гипотезы. Учитель, его отношение к учебному процессу, его творчество и профессионализм, его желание раскрыть способности каждого ребенка – вот это всё и есть главный ресурс, без которого новые требования ФГОС к организации учебно-воспитательного процесса в школе не могут существовать. Много зависит от желания и характера учителя и от уровня его профессиональной подготовки. Если человек сам по себе открыт для нового и не боится перемен, начать делать первые уверенные шаги в новых условиях он сможет в более сжатые сроки. Мы сможем реализовать новый стандарт только в том случае, если научимся быстро перестраиваться, принимать новое, органично вплетая в него традиции классической педагогики. Мне очень хотелось бы, чтобы сегодня хотя бы немного каждый из нас поверил в то, что грядущий в основной школе ФГОС не такое уж стихийное бедствие. | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||


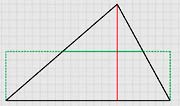
 Определите площадь прямоугольника
Определите площадь прямоугольника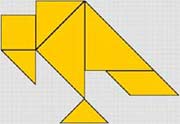
 Слайд 15
Слайд 15
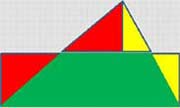
 1 вариант
1 вариант