|
Конспект урока алгебры в 8 классе по теме «Преобразование выражений, содержащих квадратные корни» по учебнику «Алгебра 8»| 1. /Конспект урока.docx | Конспект урока алгебры в 8 классе по теме «Преобразование выражений, содержащих квадратные корни» по учебнику «Алгебра 8»
|
 Конспект Конспект
урока алгебры в 8 классе
по теме «Преобразование выражений, содержащих квадратные корни»
по учебнику «Алгебра – 8» Г.В. Дорофеева, С. Б. Суворова под редакцией Г.В.Дорофеева.
Цель урока:
проверить уровень усвоения темы путем дифференцированного опроса учащихся.
Задачи урока:
формировать у учащихся адекватную самооценку при выборе уровня трудности самостоятельной работы;
развивать математическую речь при комментировании решения, при составлении алгоритмов выполнения заданий;
воспитывать навыки самоконтроля и взаимоконтроля;
развивать самостоятельность и творчество.
Оборудование: мультимедийный проектор, оценочный лист, карточки.
Деятельность учителя
|
Деятельность учащихся
|
Слайд
|
I. Организационный этап (2 мин).
Учитель сообщает тему урока, формулирует цель и задачи урока.
Звучит стихотворение великого математика 19 века Софьи Ковалевской.
Если в жизни ты хоть на мгновенье
Истину в сердце своем ощутил,
Если луч света сквозь мрак и сомненье
Ярким сияньем твой путь озарил:
Что бы в решенье твоем неизменном
Рок ни назначил тебе впереди,
Память об этом мгновенье священном
Вечно храни, как святыню в груди.
Тучи сберутся громадой нестройной,
Небо покроется черною мглой,
С ясной решимостью, с верой спокойной
Бурю ты встреть и померься с грозой.
(В этом стихотворении выражено стремление к знаниям, умение преодолевать все преграды, которые встречаются на пути).
Подвести итоги сегодняшнего урока поможет оценочный лист. Рабочая карта урока есть у каждого из учащихся. Сюда необходимо вносить баллы, полученные за каждый этап урока. Одну из оценок поставит сосед по парте, а одну – учитель, если учащийся будет работать у доски. Бонусные баллы – за активность. В конце урока будет подведен итог и выставлена отметка за усвоение темы «Арифметический квадратный корень».
|
Слушают
|
Слайд1

Слайд 2

Слайд 3
|
Диктант(8 мин)
думать придется много, писать – мало.
ДА - НЕТ
Критерии оценивания: «5» - нет ошибок
«4» - 1 – 2 ошибки
«3» - 3 – 4 ошибки
«2» - более 4-х ошибок
(кнопкой на слайде с «божьей коровкой» перейти на слайд с критериями оценивания графического диктанта)
Устная работа (7 мин).
Учащимся предлагаются задания по нарастанию уровня сложности: «Немного подумайте» - задания базового уровня, «Подумайте лучше» - повышенного.
Критерии оценивания: каждый, кто правильно ответил на вопрос, ставит в Рабочую карту урока соответствующее количество баллов: «Немного подумайте» - 1 балл, «Подумайте лучше» - 2 балла Учащиеся, верно ответившие на несколько вопросов, суммируют баллы.
Слайды меняются по щелчку, появляются правильные ответы и зачеркиваются неправильные также по щелчку.
|
Учащиеся отвечают на вопросы:
1. Корень из произведения неотрицательных множителей равен произведению корней из этих множителей (да).
2. Это верное равенство:
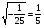 (нет). (нет).
3. Арифметическим квадратным корнем из числа а называется любое число, квадрат которого равен а (нет).
4. Корень из дроби, числитель которой неотрицательное число, а знаменатель – положительное, равен корню из числителя, деленному на корень из знаменателя (да).
5. Выражение 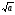 имеет смысл только при отрицательном значении а (нет). имеет смысл только при отрицательном значении а (нет).
6. Это верное равенство: 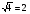 (да). (да).
7. Чтобы извлечь корень из степени с четным показателем, достаточно представить подкоренное выражение в виде квадрата некоторого выражения и воспользоваться тождеством 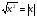 (да). (да).
8. Равенство 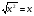 верно при любом значении х (нет). верно при любом значении х (нет).
Учащиеся отвечают на вопросы. Немного подумайте.
Вынесите множитель из-под знака корня:
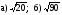
Внесите множитель под знак корня:
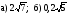
Возведите в квадрат:
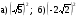
Приведите подобные слагаемые:
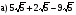
Подумайте лучше.
Найди ошибку:
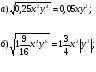
|
Слайд 5-6

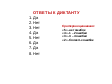
Слайд №7-13


|
Решение упражнений (8 мин).
Извлечь кубические корни из чисел (слайд 14).
Проверка осуществляется через слайд 15
|
Учащиеся решают у доски задания на извлечение кубических корней из чисел в пределах 1000000, используя таблицу кубов однозначных чисел
|
Слайды № 14-15
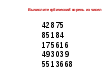
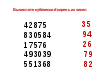
|
Тестирование (5 мин).
Герберт Спенсер, английский философ, говорил: «Дороги не те знания, которые откладываются в мозгу, как жир, дороги те, которые превращаются в умственные мышцы».
На этом этапе урока необходимо применить выученные определения и правила к решению упражнений в ходе выполнения теста.
Код правильных ответов: 21414 Критерии оценивания каждого уровня представлены на карточках и на слайде.
|
Решают задания теста, самостоятельно выбирая уровень, отвечающий их знаниям и умениям.
|
Слайд № 16

|
Подведение итогов, рефлексия (3 мин).
Выставляется итоговая отметка в оценочный лист.
На экране появляются буквы:
АОВСТЛКРИЧГНМО
Выполняя задания 1 – 7, вычеркните буквы, соответствующие ответам.
Остается слово «Отлично».
Нажимать на правильный ответ или соответствующую ему букву нет необходимости, буква исчезнет сама по щелчку, и также по щелчку следует переходить к следующему слайду.
|
Учащиеся подсчитывают общее количество баллов, полученных за урок, выставляют отметку согласно критериям.
Учащиеся устно выполняют задания:
1. 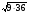 2. 2. 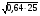 3. 3. 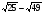 4. 4. 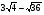 5. 5. 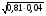
6. 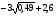 7. 7. 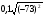
Шифр: А – 18; В – 4; Г - -2; И – 1; К – 0; М – 0,18; Н – 0,8; О - -5; Р – 0,5; С – 7,3; Т – 25; Ч – 8
|
Слайд № 17
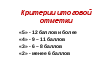
Слайды № 18-24
|
VIII. Итог урока (2 мин).
Учитель дает домашнее задание:
Урок окончен.
|
Учащиеся получают карточки с домашним заданием, приближенным к ГИА
|
| |
|
|
 Скачать 43.38 Kb.
Скачать 43.38 Kb. Конспект
Конспект

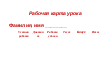
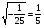 (нет).
(нет).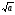 имеет смысл только при отрицательном значении а (нет).
имеет смысл только при отрицательном значении а (нет).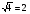 (да).
(да).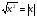 (да).
(да).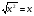 верно при любом значении х (нет).
верно при любом значении х (нет).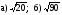
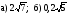
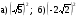
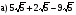
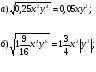



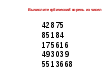
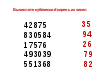

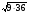 2.
2. 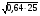 3.
3. 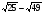 4.
4. 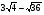 5.
5. 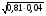
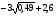 7.
7.