Вавилов Сергей Иванович
 Скачать 206.97 Kb. Скачать 206.97 Kb.
|
Введение Когда наука достигает какой-либо вершины, с нее открывается обширная перспектива дальнейшего пути к новым вершинам, открываются новые дороги, по которым наука пойдет дальше. Вавилов Сергей Иванович Есть в школьной геометрии особые темы, которые ждешь с нетерпением, предвкушая встречу с невероятно красивым материалом. К таким темам можно отнести "Правильные многогранники". Здесь не только открывается удивительный мир геометрических тел, обладающих неповторимыми свойствами, но и интересные научные гипотезы. И тогда урок геометрии становится своеобразным исследованием неожиданных сторон привычного школьного предмета, но к сожалению в школьной программе мы не углубляемся в изучение правильных многогранников, поэтому сведений об этих геометрических телах для меня недостаточно. Ни одни геометрические тела не обладают таким совершенством и красотой, как правильные многогранники. «Правильных многогранников вызывающе мало, - написал когда-то Л. Кэролл, - но этот весьма скромный по численности отряд сумел пробраться в самые глубины различных наук». На уроке в 10 классе мы изучали «Правильные многогранники» через проектную работу, где каждая группа готовила презентацию о многогранниках. Весь класс с удовольствием изучал эту тему, решали задачи, делали чертежи, поделки, готовили презентации. На уроке – проекте мы рассмотрели каждую работу. И после этого урока я задалась вопросом «Действительно ли правильные многогранники вокруг нас? Видим ли мы их так же, как видят их великие творческие люди и ученые?» Цель: Формирование представлений о правильных многогранниках, широте применения в разных предметных областях. Задачи:
2.1. Многогранники и история Геометрические знания примерно в объёме современного курса средней школы были изложены ещё 2200 лет назад в «Началах» Евклида. Евклид в своей работе опирался на труды десятков предшественников – Фалеса и Пифагора, Демокрита и Гиппократа, Архита и Теэтета, Евдокса и др. В XVII в. Декарт благодаря методу координат начал изучение свойств геометрических фигур с помощью алгебры. В XVII-XVIII вв. зарождается дифференциальная геометрия, изучающая свойства фигур с помощью методов математического анализа. В XVIII-XIX вв. появляется начертательная геометрия (основоположник – французский математик Г. Монж) и проективная геометрия (заложили основу – французские математики Д. Дезарг, Б. Паскаль и Ж.В. Понселе). В середине XIX в. Никалай Иванович Лобачевский создал новую неевклидовую геометрию, называемую ныне геометрией Лобачевского. Ученые и философы Древней Греции – Фалес, Пифагор, Демокрит, Евдокс – ездили в Египет и Вавилон для изучения музыки, математики астрономии. Зачатки греческой геометрической науки связаны с именем Фалеса Милетского, основателя ионийской школы. Ученые ионийской школы впервые подвергли логической обработке и систематизировали математические сведения, позаимствованные у древневосточных народов. Пифагор Прокл приписывает Пифагору, кроме известной теоремы о квадрате гипотенузы, еще построение пяти правильных многогранников (тетраэдра, куба, октаэдра, додекаэдра, икосаэдра), создание учения о подобии фигур. Пифагор – был среди первых ученых, рассматривавших геометрию и как практическую и прикладную дисциплину, а как абстрактную логическую науку. Пифагорейский союз Пифагорейский союз был одновременно философской школой, политической партией, религиозным братством. Эмблемой для учеников Пифагора служил так называемый звездчатый пятиугольник – фигура, которую образуют диагонали правильного пятиугольника. В школе Пифагора было открыто существование несоизмеримых величин. Правильные многогранники В дословном переводе с греческого «тетраэдр» означает «четырехгранник», октаэдр» - «восьмигранник», «гексаэдр» - «шестигранник», «додекаэдр» - «двенадцатигранник», «икосаэдр» - «двадцатигранник». Этим красивым телам посвящена 13-я книга «Начал» Евклида. Их так же изучал Театет, Гипсикл, Папп. Правильные многогранники еще называют телами Платона, так как они занимали важное место в философской концепции Платона об устройстве мироздания. Четыре многогранника олицетворяли в ней четыре сущности или «стихии». Стихиями натурфилософы называли вещества, из которых путем сгущения и разряжения, охлаждения и нагревания образуются все тела. Стихии и многогранники Пифагорейцы считали, что огонь состоит из мельчайших тетраэдров, так как тетраэдр обладает наименьшим числом граней и наиболее «острыми» многогранными углами при вершинах, а значит, обладает наибольшей проникающей способностью. Обладает рациональной конструкцией: высокой прочностью при малом весе. Итак, тетраэдр символизировал огонь, так как его вершина устремлена вверх; икосаэдр – воду, так как он самый «обтекаемый»; куб – землю, как самый «устойчивый»; октаэдр – воздух, как самый «воздушный»; додекаэдр, воплощал в себе «все сущее», символизировал все мироздание, считался главным. Взаимоотношения между стихиями по Платону. Уравнение: 1 вода = 2 воздух + 1 огонь. Надо понимать так: в элементе воды – икосаэдре – 20 граней, образованных равносторонними треугольниками, которые, в свою очередь состоят из 6 прямоугольных треугольников. По Платону, атомы – плоские тела – прямоугольные треугольники двух видов: равнобедренные и с катетом, равным половине гипотенузы. Значит, сложный атом икосаэдр состоит из 6 × 20 = 120 простых атомов – треугольников. В элементе воздуха – 8 граней, значит общее число треугольников 48 × 2 = 96. Итак, равенство верно: 20 граней и 120 треугольников (8 × 2 + 4) граней и (48 × 2 + 24) треугольников. 2.2.Правильные многогранники в математике Многогранник называется правильным, если: он выпуклый, все его грани – равные правильные многоугольники, в каждой вершине сходится одинаковое число граней, все его двухгранные углы равны. Правильных многогранников вызывающе мало, но этот весьма скромный по численности отряд сумел пробиться в самые глубины различных наук. (Л.Кэрролл). Человек проявляет интерес к многогранникам на протяжении всей своей сознательной деятельности – от двухлетнего ребенка, играющего деревянными кубиками, до зрелого математика. Некоторые из правильных тел встречаются в природе в виде кристаллов, другие в виде вирусов (которые можно рассмотреть с помощью электронного микроскопа). Пчелы строили шестиугольные соты задолго до появления человека, а в истории цивилизации создание многогранных тел (подобных пирамидам) наряду с другими видами пластических искусств уходит в глубь веков. Сколько правильных многогранников существует? Пусть при одной вершине сходится n – ребер, тогда плоских углов при вершине будет тоже n. И все они равны между собой. Пусть x – один из плоских углов, тогда сумма плоских углов при вершине – nx. По свойству плоских углов nx< 360,x<  . Угол правильного n – угольника равен α = . Угол правильного n – угольника равен α = 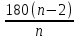 Начиная с n =7, угол станет меньше 60 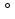 , а такого правильного n-угольника не существует. , а такого правильного n-угольника не существует. 1. Грани правильного многогранника – правильные треугольники, тогда 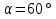 1) 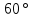 × 3=180 × 3=180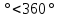 , 4 грани – тетраэдр. , 4 грани – тетраэдр.2) 60 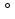 × ×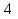 = =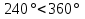 , 8 граней – октаэдр. , 8 граней – октаэдр.3) 60 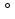 × 5= × 5=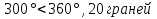 - икосаэдр. - икосаэдр.60 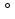 ×6 = 360 ×6 = 360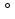 - это противоречит теореме о сумме плоских углов многогранного угла, значит больше правильных многогранников, грани которых – правильные треугольники не существует. - это противоречит теореме о сумме плоских углов многогранного угла, значит больше правильных многогранников, грани которых – правильные треугольники не существует.2. Грани правильного многогранника – квадраты, тогда 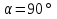 1). 90 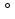 ×3 = ×3 = 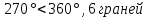 - гексаэдр (куб) 2). 90 - гексаэдр (куб) 2). 90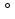 × 4 = × 4 = 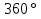 - это значит, что больше правильных многогранников, грани которых – квадраты не существует. - это значит, что больше правильных многогранников, грани которых – квадраты не существует.3. Грани правильного многогранника – правильные пятиугольники, тогда 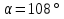 1). 108 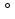 ×3 = ×3 = 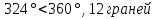 – додекаэдр. – додекаэдр.2). 108 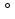 × 4 × 4 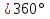 - это значит, что больше правильных многогранников, грани которых – правильные пятиугольники не существует. - это значит, что больше правильных многогранников, грани которых – правильные пятиугольники не существует. 4. Начиная с правильного шестиугольника 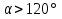 Следовательно, n× 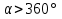 (n>3), поэтому правильных многогранников, грани которых – правильные многоугольники с числом сторон больше 5, не существует. (n>3), поэтому правильных многогранников, грани которых – правильные многоугольники с числом сторон больше 5, не существует.Итак, мы доказали, что существует пять и только пять правильных выпуклых многогранников. Доказательство того, содержится в «Началах» Евклида. Формула Эйлера Изучая любые многогранники, естественнее всего подсчитать, сколько у него граней, ребер и вершин. Подсчитаем и мы число указанных элементов правильных многогранников и зафиксируем результаты в таблице. Сумма числа граней и вершин равна числу ребер, увеличенному на 2: Г + В = Р + 2. Эта формула была подмечена уже Декартом в 1640 году, а позднее переоткрыта Эйлером (1752), имя которого с тех пор она и носит. Формула Эйлера верна для любых выпуклых многогранников.
Двойственность ли сопряженность правильных многогранников. Если центры граней куба соединить отрезками, то получится октаэдр, то есть вписанный в куб октаэдр. Обратно: центры граней октаэдра являются вершинами вписанного куба. Двойственными являются икосаэдр и додекаэдр. Тетраэдр двойственен сам себе. 2.3.Многогранники в биологии: 2.3.1.Связь многогранников с живой природой Встречаются ли в живой природе правильные многогранники? Фрагмент книги немецкого биолога Э. Геккеля "Красота форм в природе""Природа вскармливает на своем лоне неисчерпаемое количество удивительных созданий, которые по красоте и разнообразию далеко превосходят все созданные искусством человека формы".Создания природы, красивы и симметричны. Это неотделимое свойство природной гармонии. Скелет одноклеточного организма феодарии (Circogoniaicosahedra) по форме напоминает икосаэдр. Большинство феодарий живут на морской глубине и служат добычей коралловых рыбок. Простейшее животное пытается себя защитить: из 12 вершин скелета выходят 12 полых игл. На концах игл находятся зубцы, делающие иглу еще более эффективной при защите. Чем же вызвана такая природная геометризация феодарий? Тем, что из всех многогранников именно икосаэдр имеет наибольший объем при наименьшей площади поверхности. Это свойство помогает морскому организму преодолевать давление водной толщи. Водоросль. Вольвокс - один из простейших многоклеточных организмов, представляет собой сферическую оболочку, сложенную в основном семиугольными, шестиугольными и пятиугольными клетками, то есть клетками, имеющими семь, шесть или пять соседних; в каждой «вершине» сходятся три клетки. Соты пчелиные — наиболее совершенные постройки насекомых. Соты пчелиные - восковые постройки пчёл, предназначенные для хранения запасов корма и выращивания потомства. Соты пчелиные состоят из шестигранных призматических ячеек, которые заполняют пространство без просветов. Верхняя часть пчелиной ячейки представляет собой часть ромбододекаэдра. В разрезе соты представляют сеть равных правильных шестиугольников. Из правильныхn-угольников с одинаковой площадью правильные шестиугольники имеют наименьший периметр. Т.О. мудрые пчёлы экономят воск и время для постройки сот. Приложение 1. 2.3.2.Вирусы Вирусы (от лат. Virus — яд), возбудители инфекционных болезней растений, животных и человека. Размножаются только в живых клетках. Вирусы мельче большинства известных микробов. В отличие от бактерий, вирусы не удаётся культивировать на обычных питательных средах. Для экспериментальных и медицинских целей (получения вакцин и др.) их культивируют в животных и растительных организмах. Вирусы вызывают многие заболевания: оспу, корь, грипп, полиомиелит, чуму рогатого скота и птиц, бешенство и др. Вирусы, поражающие бактерии - бактериофаги. Форма вирусов Вирус не может быть совершенно круглым, как считалось раньше. Для того чтобы определить его форму, брали разные многогранники, направляли на свет под теми же углами, что и поток атомов на вирус. Оказалось, что только один многогранник 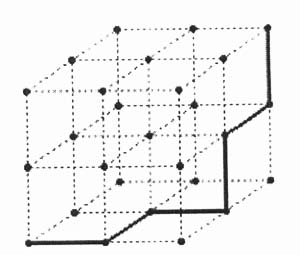 дает точно такую же тень – икосаэдр. Форма вирионов очень разнообразна: у вируса полиомиелита и жёлтой мозаики турнепса — многогранные шарики. 2.4. Правильные многогранники и химия Правильные многогранники - самые выгодные фигуры. И природа этим широко пользуется. Поваренная соль NaCl - она хорошо растворима в воде, служит проводником электрического тока, кристаллы поваренной соли имеют форму куба. Производство алюминия используют алюминиево-калиевые квасцы K[Al(SO4)2]·12H2O,монокристалл которых имеет форму правильного октаэдра. Получение серной кислоты, железа, особых сортов цемента используют сернистый колчедан FeS–пирит. Кристаллы этого химического вещества имеют форму додекаэдра. Использование в химических реакциях сурьмянистый сернокислый натрий Na5(SbO4(SO4) – вещество, синтезированное учеными. Кристалл сурьмянистого сернокислого натрия имеет форму тетраэдра. Использование в электротехнике икосаэдр передает форму кристаллов бора. В свое время бор использовался для создания полупроводников первого поколения. Из школьного курса химии мы знаем, что модели молекулы метана, зеркальных изомеров молочной кислоты являются тетраэдрами. Кристаллы медного купороса представляют собой октаэдры; кристаллические решетки имеют многие металлы:Li, Na, Cr, Pb, Al, Au, Cu. Кристаллическую решетку имеют соли CsCl, кислой соли K2[PtCl6].Правильные многогранники определяют форму кристаллических решеток некоторых химических веществ. 2.4.1.Кристаллография Кристаллография (от кристаллы и ...графия), наука о кристаллах и кристаллическом состоянии вещества. Изучает симметрию, строение, образование и свойства кристаллов. Кристаллография зародилась в древности в связи с наблюдениями над природными кристаллами, имеющими естественную форму правильных многогранников. Как самостоятельная наука существует с середины 18 в. Развивалась в тесной связи с минералогией как дисциплина, устанавливающая закономерности огранки кристаллов (Р. Аюи, 1784). Кристаллы - твёрдые тела, имеющие естественную форму правильных многогранников. От греч. krýstallos, первоначально — лёд, в дальнейшем — горный хрусталь. Кристаллы образуются и растут чаще всего из жидкой фазы — раствора или расплава, возможно получение их из газовой фазы. Первый закон геометрии кристаллографии открыт в 1669г. Углы между соответствующими гранями кристалла одного и того же вещества постоянны—закон постоянства углов открыл Николай Стено (1638-1687 гг.). Н. Стено провёл измерения на ромбододекаэдрах граната – состоящего из граней одного типа. Все двугранные углы ромбододекаэдра равны, это ставит его в ряд правильных многогранников, но многогранные углы не равны. Есть вершины, в которых сходятся по три и четыре ребра, то из равенства всех двугранных углов не следует равенство всех многогранных углов этого многогранника. Простейшие элементы симметрии кристаллов. Приложение №2. 2.5. Многогранники и искусство Большой интерес к формам правильных многогранников проявляли и проявляют скульпторы, архитекторы, художники. Их всех поражало совершенство, гармония многогранников. Сальвадор Дали на картине «Тайная вечеря» (1955 г)изобразил И. Христа со своими учениками на фоне огромного прозрачного додекаэдра.  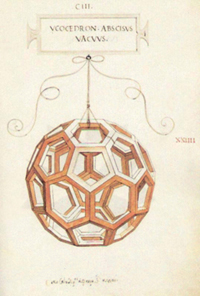 Леонардо да Винчи (1452 — 1519) увлекался теорией многогранников и часто изображал их на своих полотнах. Например, он проиллюстрировал изображениями правильных и полуправильных многогранников книгу своего друга монаха Луки Пачоли (1445 — 1514гг.) «О божественной пропорции» (1959 г.) Изображение Леонардо да Винчи усеченного икосаэдра методом жестких ребер.   Титульный лист книги Ж. Кузена Надгробный памятник в кафедральном «Книга о перспективе» соборе Солсбери Сэру Томасу Джорджсу. Кубические пространственные решетки в изображении Леонардо.  Этим изображением Леонардо на три века предвосхитил гипотезу о периодическом строении кристаллов, высказанную французскими кристаллографами аббатом Рэнэ-Жюстом Гаюи (1743-1822гг.)и морским офицером Огюстом Бравэ (1811-1863) Альбрехт Дюрер (1471 — 1528)  Знаменитый художник эпохи возрождения на переднем плане своей гравюры «Меланхолия» изобразил додекаэдр. В 1525 году он написал трактат, в котором представил пять правильных многогранников, поверхности которых служат хорошими моделями перспективы. Интарсии работы Фра Джовани да Верона, созданные для церкви SantaMariain  Organo в Вероне. Organo в Вероне.Маурица Эшер (1898-1972) «Звезды» (1948),  Мауриц Эшер в своих рисунках как бы открыл и интуитивно проиллюстрировал законы сочетания элементов симметрии, т.е. те законы, которые властвуют над кристаллами, определяя и их внешнюю форму, и их атомную структуру, и их физические свойства. Графическая фантазия Маурица Эшера «Рептилии» (1943). Эшер увлекается периодическими рисунками, составлением мозаичных узоров из повторяющихся фигур. Он вписывает или, вернее, вписывает одно изображение вдругое, так чтобы одинаковые фигурки периодически повторялись, и между ними не оставалось пустых мест». Как, например, между рептилиями, не успевшими выбраться с журнальной страницы.  Но ведь это и есть закон, по которому размещаются частицы в структуре кристалла — закон плотнейшей упаковки. Для понимания любой картины Эшера требуется внимание и наблюдательность. «Ячейки кубического пространства» Эшера (1952 г.)   Литография «водопад» В центре картины - комплекс конструкций на фоне ландшафта с террасами. На башнях– 3 пересекающихся куба и 3 – октаэдра. В центре – ручей, падающий на колесо и крутящий его. Он течет через башни, трижды протекая через точку, в которой уже проходил. Абсурдность доходит до нас через «круг» неправильных соединений куба. Т.О Архитектура  История человеческой цивилизации - это история экспериментов человека с материалами и конструкциями. Подбирая разнообразные их сочетания, он стремился с минимальными затратами добиться максимального эффекта. И ни один человек в мире не приблизился к этой цели в большей степени, чем Р. Бакминстер Фуллер- философ, математик, инженер, историк, поэт и, помимо всего прочего, изобретатель геодезических куполов.  40-е годы упомянутый Бакминстер Фуллер, исходя из структуры древнегреческого икосаэдра, создал Димаксион, или геодезический купол, предназначенный для использования в архитектурных сооружениях. На рис. Димаксион Геодезические купола как наиболее эффективные строительные системы  Геодезический купол - это не просто совокупность треугольников, соединенных особым образом. Геометрическая симметрия порождает сочетание прочности и компактности и создает эффект беспрецедентной новизны. 2.6. Многогранники и устройство мира по И. Кеплеру Устройство мира по И. Кеплеру немецкий астроном, математик и великий фантазер Иоганн Кеплер (1571-1630). Гармония Иоганна Кеплера интересы Кеплера были чрезвычайно широки, но сам он всю жизнь считал себя математиком, подписываясь «математикус Кеплер».Кеплер определил классы многогранников, в частности тот, который мы называем архимедовыми телами, описал каждый из многогранников (некоторые — впервые). В своей книге «Мировая гармония» («Harmonice Mundi», 1619 г.)он математически доказал, что класс архимедовых тел исчерпывается описал  класс Платоновых тел и изобразил два звездных правильных тела. На рисунке Кеплера, иллюстрирующем этот класс, многогранник за номером 13 открыт им самим, остальные были описаны ранее художниками Возрождения. Термин «усеченный икосаэдр» введен Кеплером. 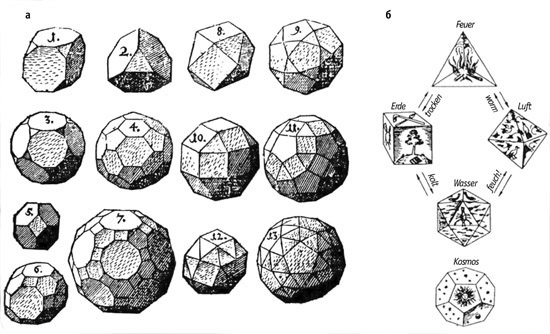 Изображение двух звездных правильных многогранников. Ещё одним выдающимся вкладом Кеплера в геометрию многогранников является открытие им двух звездных правильных тел Всего их четыре; два других нашел французский математик Луи Пуансо в 1809 г. 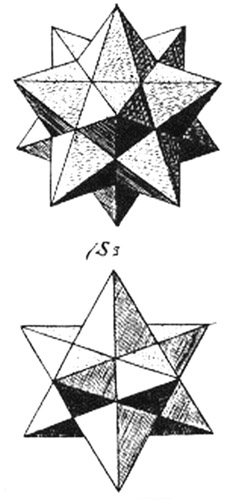 В работе «Конспект астрономии Коперника» (в двух томах) 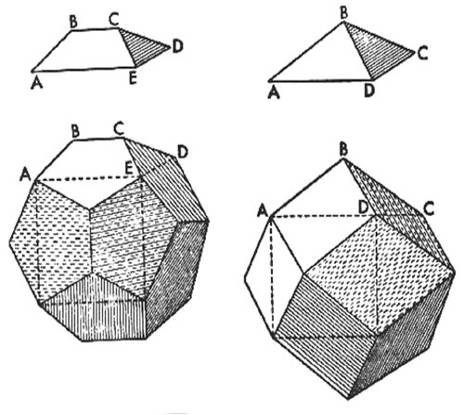 Кеплер обращается к геометрии многогранников, в частности, вслед за Эвклидом предлагает способ «конструирования» додэкаэдра и ромбического додэкаэдра с помощью добавления своего рода «крыши» к каждой из шести граней куба. Основной вклад Кеплера в науку — это, конечно, открытые им три закона движения планет относительно Солнца. Первый закон: каждая планета движется по эллипсу, в одном из фокусов которого находится Солнце. Второй закон: каждая планета движется в плоскости, проходящей через центр Солнца, причем площадь сектора орбиты, описанная радиусом-вектором, изменяется пропорционально времени. Третий закон: квадраты времени обращения планеты вокруг Солнца относятся, как кубы их средних расстояний от Солнца. Но это были только гипотезы, пока их не объяснил и уточнил на основе закона всемирного тяготения Исаак Ньютон (1643-1727), место правильных многогранников в системе гармоничного устройства мира по Кеплеру описанное в сочинении «ВВЕДЕНИЕ» т.к. существует всего пять правильных многогранников, им соответствуют шесть планет Солнечной системы: Меркурий, Венера, Земля, Марс, Юпитер, Сатурн. Кеплер предположил, что сферы планет связаны между собой вписанными в них Платоновыми телами. Так как для каждого правильного многогранника центры вписанной и описанной сфер совпадают, то вся модель будет иметь единый центр, в котором располагается Солнце. Модель Солнечной системы Кеплера получила название «Космического кубка». 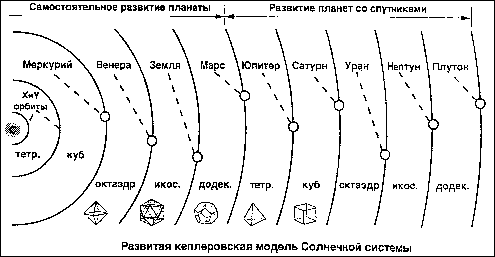 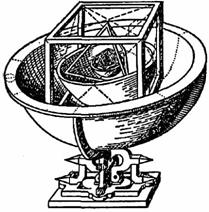 В сферу орбиты Сатурна можно вписать куб, в который вписывается сфера орбиты Юпитера. В нее, в свою очередь, вписывается тетраэдр, описанный около сферы орбиты Марса. В сферу орбиты Марса вписывается додекаэдр, в который вписывается сфера орбиты Земли. А она описана около икосаэдра, в который вписана сфера орбиты Венеры. Сфера этой планеты описана около октаэдра, в который вписывается сфера Меркурия. Глядя на эту иллюстрацию Кеплера, понимаешь: в то время, чтобы изобразить такое, ученый обязан был быть мастером графики, а в данном случае—и скульптором. Кеплер изготовил трехмерную модель своей «Солнечной Системы» из цветной бумаги и надеялся так же воспроизвести ее в серебре. Более двух лет заняли у Кеплера вычисления расстояний по его гипотезе о взаимосвязи числа планет и их орбит с числом платоновых тел, а также их многократная проверка. В конце концов, Кеплеру пришлось признать ошибочность 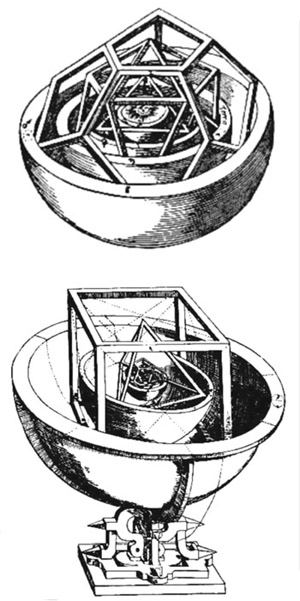 гипотезы, высказанной во «Введении...». По словам выдающегося французского ученого (астронома, физика, математика и метеоролога) и политического деятеля, популяризатора и историка науки (в частности, биографа Кеплера) Доминика Франсуа Араго (1786-1853), «без гипотез наука не может двигаться вперед — без них нельзя придумать ни одного опыта; но в обращении с гипотезами нужно быть добросовестным и допускать их в науку лишь после тщательной проверки». Кеплер всегда был верен этому правилу: от самых любимых своих гипотез он отказывался без всяких колебаний, если они не подтверждались наблюдением и вычислением». 2.6.1.Гипотеза о строении Земли Икосаэдро-додекаэдровая структура Земли Научная гипотеза о связи правильных многогранников с гармоничным устройством мира. Гипотеза московских инженеров В. Макарова и В. Морозова. (80-е годы).Они считают, что ядро Земли имеет форму и свойства растущего кристалла, оказывающего воздействие на развитие всех природных процессов, идущих на планете. Лучи этого кристалла, а точнее, его силовое поле, обуславливают икосаэдро-додекаэдровую структуру Земли проявляется в том, что в земной коре как бы 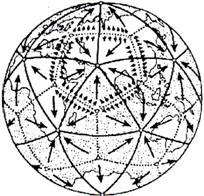 проступают проекции вписанных в земной шар правильных многогранников: икосаэдра и додекаэдра. Многие залежи полезных ископаемых тянутся вдоль икосаэдро-додекаэдровой сетки. 62 вершины и середины рёбер многогранников, называемых авторами узлами, обладают рядом специфических свойств, позволяющих объяснить некоторые непонятные явления. Здесь располагаются очаги древнейших культур и цивилизаций: Перу, Северная Монголия, и др. В этих точках наблюдаются максимумы и минимумы атмосферного давления, гигантские завихрения Мирового океана. В этих узлах находятся озеро Лох-Несс, Бермудский треугольник. 3. Заключение Подбирая материал для своей работы, я познакомилась с различными видами многогранников (правильные, неправильные, звездчатые). Узнала, где они встречаются в природе (кристаллы, соты, снежинки, феодария) и окружающем нас мире (головоломки, пирамиды, картины). Решая поставленную проблему, я увидела, что многогранники действительно окружают меня везде – это крупинки сахара и соли, камень в кольце мамы, форма зданий и деревьев и многое другое. В своей работе я попыталась описать эти древние пространственные фигуры, чтобы расширить свое представление о них. Думаю, что собранный материал будет мне полезен и в дальнейшем… 4. Список литературы 1.Банн Ч., Кристаллы, пер. с англ., М., 1970 2. Гольдфарб Д. М., Бактериофагия, М., 1961 3. Гросман С., Тернер Дж. Математика для биологов. М., 1983 4.Зильбер Л. А., Вирусо-генетическая теория возникновения опухолей, М., 1968 5. Ильченко В.Р. Перекрёстки физики, химии, биологии. – М.: Просвещение, 1986, с.102 6.КостовИ., Кристаллография, пер. сболг., М., 1965 7. Кривиский А. С., Проблемы бактериофагии, в сборнике: Актуальные вопросы вирусологии, М., 1960 8. Крицман В.А. - сост. Книга для чтения по неорганической химии. – М.: Просвещение, 1993, с. 10 –13 9. LwoffА., HorneR., TournierP., Asystem of viruses, вкн.: Gold Spring Harbor Symposia on quantitative biology, v. 27, N. Y., 1962, p. 51—55 10. Най Дж., Физические свойства кристаллов и их описание при помощи тензоров и матриц, пер. с англ., 2 изд., М., 1967 11. Раутенштейн Я. И., Бактериофагия, М., 1955 12. Стент Г., Молекулярная биология вирусов бактерий, пер. с англ., М., 1965 13.Шаскольская М., Кристаллы, М., 1959 14.Шубников А. В., Флинт Е. А., Бокий Г. Б., Основы кристаллографии, М.— Л., 1940 Приложение №1 Восковые постройки пчёл На рисунке показано, как соприкасаются ячейки в улье: их общая часть является ромбом. В этом случае площадь поверхности многогранника – ячейки меньше площади поверхности правильной шестиугольной призмы. При такой «математической» работе пчёлы экономят 2 процента воска. 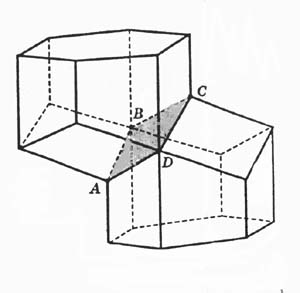 Приложение №2 Кристаллография Микромонокристалл Монокристалл германия сегнетовой соли.   Природные кристаллы турмалина. Кристаллы белка каталазы (увеличено).   Постоянство межгранных углов данного кристалла при разном развитии граней. 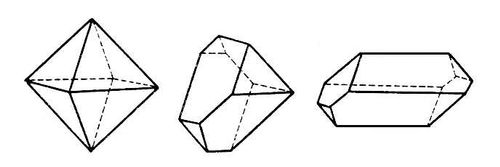 Всего существует 32 класса симметрии кристаллических многогранников. 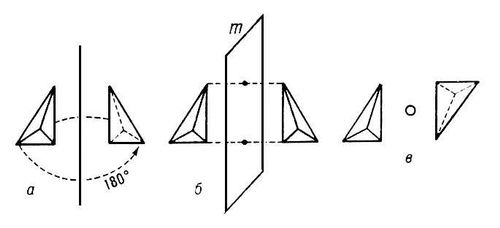 а — ось симметрии - совмещает фигуру с собой поворотом на 360°/N (N — порядок оси симметрии); б — плоскость симметрии m — совмещает фигуру «отражением»; в — центр симметрии — действует как поворот и отражение одновременно. Округлость граней и рёбер  Вицинальные формы и холмики роста на грани кварца. Вицинальные формы и холмики роста на грани кварца.Пластинчатые, игольчатые, нитевидные кристаллы.  Нитевидные кристаллы AIN (электронно -микроскопическое изображение). Нитевидные кристаллы AIN (электронно -микроскопическое изображение).Ветвистые (дендритные) кристаллы типа снежинок.  Дендриты хлористого аммония. Дендриты хлористого аммония. Монокристальная «буля» рубина (длина 20 см).  Некоторым кристаллам уже в процессе выращивания придаётся форма требуемого изделия - трубы, стержня пластинки. Некоторым кристаллам уже в процессе выращивания придаётся форма требуемого изделия - трубы, стержня пластинки. Алмазы Архангельской области.   Месторождения: им. М,В, Ломоносова, трубка им. Карпинского – 1, Карпинского – 2, тр. Пионерская, тр. Архангельская. Основная доля алмазов представлена в виде кривогранных ромбододекаэдров, Переходными габитусами, Октаэдрами, Тетрагексаэдрами. 17 февраля, 2012 | ||||||||||||||||||||